Файл: Сені олынан брі келеді, тек зіе сен (кейбір сратарды жауабын таба алмадым, барымша істедім) жне матрицалары берілген.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 102
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2cos(2x+3)
#4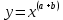 функциясының туындысы тең:*+
функциясының туындысы тең:*+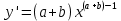
#5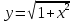 функциясының дифференциалы қай өрнекке сәйкес
функциясының дифференциалы қай өрнекке сәйкес
#6 y = 2x3 - 5x2 + 7x + 4 функциясының туындысы неге тең? *+6x2-10x+7
#7 y = eax функцияның екінші ретті туындысы неге тең? *+a2eax
#8 !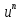 , мұндағы
, мұндағы  , функциясының туындысы тең *+шексіз аз
, функциясының туындысы тең *+шексіз аз
#9 y =sin2x функциясының туындысы тең 2cos2x(Өзім жаздым тексеріп көр)
#10 y=(2x-3)3 функциясының екінші ретті дифференциалы қай өрнекке сәйкес*+24(2x-3) dx2
#11y = 5 x5 функциясының үшінші ретті туындысы: *+300 x2
#12 y = eax функциясының екінші ретті туындысы:+a2eax
#13 (2х-5)dx өрнегі ... функциясының дифференциалына сәйкес*+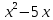
#14 y = 2x3 - 5x2 +7x +4 функциясының туындысы тең *+6x2-10x+7
1. Оқиға-қандай да бір сынау нәтижесінде пайда болатын кез-келген факт
2. Ықтималдықтың классикалық анықтамасы: қолайлы жағдайлар санының барлық мүмкін болатын жағдайлар санына қатынасы
3. Толық топ құрайтын екi үйлесiмсiз оқиға :*+қарама-қарсы
4. А және В –қарама-қарсы оқиғалары болса және Р(А)=1/6. Онда Р(В) тап: 5/6
4. Элементар оқиғалар кеңiстiгi: барлық мүмкін болатын элементар оқиғалар жиынтығы
5. А1, А2,…,Аn оқиғаларының кемiнде бiреуiнiң пайда болу ықтималдығы: P(A)=1-q1q2…qn
6. А және В оқиғаларының көбейтiндiсi : Осы оқиғалардың бірге пайда болуынан тұратын С оқиғасы
7. А және В оқиғаларының қосындысы: А оқиғасының немесе В оқиғасының пайда болуынан тұратын с оқиғасы
8. Тәуелсiз оқиғалардың бiрге пайда болу ықтималдығы: *+осы оқиғалардың ықтималдықтарының көбейтiндiсiне тең
9. Тәуелдi оқиғалардың бiрге пайда болу ықтималдығы : +бiр оқиға ықтималдығының екiншi оқиғаның шартты ықтималдығына көбейткенге тең
10. Сынау нәтижесiнде мiндеттi түрде пайда болатын оқиға : ақиқат
11. А оқиғасы толық топ құрайтын үйлесiмсiз В1, В2, …, Вn оқиғаларының бiрi орындалғанда ғана пайда болады. Бұл оқиғалардың қайсысы орындалатыны алдын ала белгiсiз болғандықтан, олар : жорамалдар
11. Кездейсоқ оқиғаның ықтималдығы: 0
11. Ақиқат оқиғаның ықтималдығы: 1
12. Р(А+В) символы ненi бiлдiредi? А немес В оқиғасының пайда болуының ықтималдығы
13. Толық ықтималдық формуласы++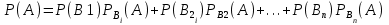
14. Байес формуласы +++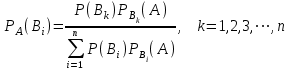
15. "Студент" сөзiнен сәтiне қарай бiр әрiп таңдалды. Таңдалынған әрiптiң дауысты болу ықтималдығы +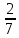
16. Жәшiкте 3қара, 5ақ, 4 қызыл шар бар. Сәтiнеқарайбiршаралынды. Алынған шардың қызыл емес болуының ықтималдығы неге тең.+ 2/3
17. Бiр жәшiкте 20 қорап анальгин, 50 қорап цитрамон және 30 қорап кофеин бар. Жәшiктен кездейсоқ қорап алынған. Алынған қораптың цитрамон немесе кофеин болу ықтималдығы 0,8
18. Жәшiкте 6 ақ, 4 қара шар бар. Кездейсоқ жәшiктен екi шар алынған. Алынған шардың екеуiнiң де ақ болу ықтималдығы 1/3
19. Екі мерген бір - біріне тәуелсіз нысанаға оқ атты. Бірінші мерген үшін нысанаға дәл тию ықтималдығы 0,7 –ге, екінші үшін 0,8-ге тең. Нысанаға дәл тию ықтималдығы 0,94
20. Екі мерген бір - біріне тәуелсіз нысанаға оқ атты. Бірінші мерген үшін нысанаға дәл тию ықтималдығы 0,7-ге тең, екінші мерген үшін 0,8-ге тең. Екі мергеннің бір мезгілде нысанаға дәл тию ықтималдығы +0,56
21. Екі мерген бір - біріне тәуелсіз нысанаға оқ атты. Бірінші мерген үшін нысанаға дәл тию ықтималдығы 0,7-ге тең, екінші мерген үшін 0,8-ге тең. Тек бір мергеннің нысанаға дәл тию ықтималдығы 0,38
22. Тұмау эпидемиясы кезінде ауруханаға жеткізілген 15 адамның ішіндегі 5-ң аяғы сынған. Палатаға 4 адамнан жатқызды. Жатқызылған адамдардың ішінде кем дегенде біреуінің аяғы сынған болып шығу ықтималдығы 11/13
23. Препараты стандарттылыққа екі фармацевттің бірімен тексеріледі. Препаратың бірінші фармацевтке түсу ықтималдығы 0,55, ал екінші фармацевтке – 0,45. Препаратты бірінші фармацевт стандартты деп қабылдау ықтималдығы 0,9, ал екінші фармацевт – 0,98. Препарат тексеру кезінде стандарты деп қабылданды. Бұл препаратты екінші фармацевт тексергендігінің ықтималдығын табыңыз 0,471
24. Әртүрлі перфораторда перфокарталардың бірдей жиынында екі перфораторшы берді. Бірінші перфораторшының қате жіберу ықтималдығы 0,05 тең, ал екінші перфораторшынікі 0,1 тең. Перфоратты тексеру кезінде қате табылуының ықтималдығын табыңыз 0,075
25. Бірдей формадағы 2 жәшік бар. 1-ші жәшікте 3 ақ, 2 қара, ал 2-ші жәшікте – 4 ақ және 3 қара шар бар. Кездейсоқ кез келген жәшіктен 1 шар алынады. Алынған шар ақ шар. Шар 1-ші жәшіктен алынғандығының ықтималдығын табыңыз. 0,59
26. Студент емтиханның 24 сұрағының тек 20–ын біледі. Бір билетте 3 сұрақ бар. Оған ең болмағанда бір дайындалмаған сұрағы бар билет түсу ықтималдығы 221/506
27. Жол апатында 12 адам зардап шекті, оның 4-і аяғын күйдіріп алды. Жедел жәрдем емханаға екі адамнан тасиды. Машинадағы екі адамның да аяғы күйген болып шығу ықтималдығы 1/11
28. Бөлімде 4 палата бар. Түнімен оттегі жастығын қажает ету ықтималдығы бірінші палата үшін – 0,2, екінші - 0,3, үшінші - 0,2, төртінші – 0,1. Түн ішінде екінші немесе үшінші палатаға оттегі жастығының қажет ету болып қалу ықтималдығы 0,5
кездейсоқ шамалар. 28 тест
#1
*! Х дискретті кездейсоқ шаманың математикалық күтімі төмендегі формула бойынша есептеледі +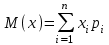
#2
*! Х және У тәуелсіз кездейсоқ шамалардың математикалық күтімдері мен дисперсиялары сәйкесінше М(Х)=2, D(X)=3, М(Y)=4, D(Y)=5 тең. Егер Z кездейсоқ шамасы Z=2X-Y+3 тең болса, М(Z) және D(Z) табыңыз:
+М(Z) = 3, D(Z)=4
#3
*! Тұрақты көбейткіш дисперсияның алдына D(CX)= +C^2D(x)
#4
*!Кездейсоқ шамалардың дисперсияларының қосындысы(айырымы) тең: +D(X+-Y)=D(x)+-D(y)
4.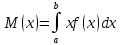 шамасы: үздіксіз кездейсоқ шаманың математикалық күтімі
шамасы: үздіксіз кездейсоқ шаманың математикалық күтімі
#5
*!Дискретті кездейсоқ шама Х таралу заңдылығымен берілген. Р1 ықтималдығын табыңыз?
0,2
#6
*!Дискретті кездейсоқ шама Х таралу заңдылығымен берілген.
0,3
р3 ықтималдығын табыңыз?
#7*! Тұрақты шаманың дисперсиясы тең …:D (С)=0
#8
*!Х кездейсоқ шамасын k тұрақты көбейткішке көбейткенде, оның математикалық күтімі қалай өзгереді: к-ға көбейтіледі
#9
*!Х кездейсоқ шамаға а саны қосылды. Осыдан оның дисперсиясы қалай өзгереді?
өзгермейді
#10
*!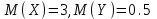 .
. 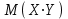 есептеңіз?1,5
есептеңіз?1,5
#11
*!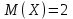 ,
,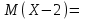 есептеңіз?-2
есептеңіз?-2
#12
*!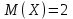 . М(2Х)= есептеңіз?4
. М(2Х)= есептеңіз?4
#13
*!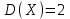 ,
, 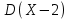 =есептеңіз?0
=есептеңіз?0
#14
*!Х дискретті кездейсоқ шамасының таралу заңдылығы берілген, М(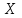 ) табыңыз
) табыңыз
М(х)=2,6
#15
*!X және Y - тәуелсіз кездейсоқ шамалар,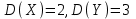 .
. 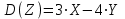 есептеңіз: Д=3*2-4*3=-6
есептеңіз: Д=3*2-4*3=-6
#16
*!X және Y- тәуелсіз кездейсоқ шамалар,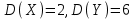 .
. 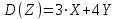 есептеңіз: D=3*2+4*6=6+24=30
есептеңіз: D=3*2+4*6=6+24=30
#17
*!Х дискретті кездейсоқ шамасының таралу заңдылығы берілген, D(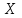 ) табыңыз.
) табыңыз.
D=7
#18
*!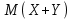 үшін формуласын табыңыз: M(X+Y)= M(X)+ M(Y)
үшін формуласын табыңыз: M(X+Y)= M(X)+ M(Y)
#19
*!Х дискретті кездейсоқ шамасының дисперсиясының формуласы:
D(x)= M[x-M(x)]2
D(x)=M(x2)- [M(x)]2
#20
*! D (CX) үшін формуласын табыңыз:
D(CX)=C2D(x)
#21
*!D(X)=2, D(3X-1)= есептеңіз:2*3-1=5
#22
*!Таралу заңымен берілген, Х дискретті кездейсоқ шамасының математикалық күтімі неге тең:
M(x)=4.9
#23
*! Дискретті кездейсоқ шама Х таралу заңдылығымен берілген. М( )=2,6. У табыңыз:
)=2,6. У табыңыз:
Y=5
#24
*! Дискретті кездейсоқ шама Х таралу заңдылығымен берілген. М( )=6,
)=6, табыңыз:
табыңыз:
X1=2
P2=0.2
#25
*! Дискретті кездейсоқ шама Х таралу заңдылығымен берілген. у есептеңіз:
Y=0,3
#26
*! Х дискретті кездейсоқ шамасының дисперсиясы:
D(x)= M[x-M(x)]2
D(x)=M(x2)- [M(x)]2
#27
*! Дискретті кездейсоқ шама Х таралу заңдылығымен берілген. D( ) есептеңіз:
) есептеңіз:
5/4
#28
*!Дискретті кездейсоқ шама Х таралу заңдылығымен берілген. М( ) есептеңіз:
) есептеңіз:
-1/2
Қайталанбалы сынаулар. 56 тест
#1
*! Бернулли формуласы: Pn(K)=Cknpkqn-k
тендеуі: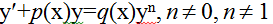
#2
*! Лапластың интегралдық формуласы қандай ықтималдықтарды есептейдi:+оқиғаның n сынауда k1-ден k2-ге дейiн пайда болуын.
# 3. Егер А оқиғасының пайда болу ықтималдығы әрбір сынауда 0,25 тең
болса, онда А оқиғасы 1000 сынауда 250ден 300ге дейін болу ықтималдығын табу үшін қандай формулаға саласыз: Муавр-Лаплас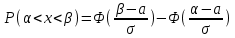 немесе Лапластың интегралдық формуласы
немесе Лапластың интегралдық формуласы
#4
*! Егер А оқиғасының пайда болу ықтималдығы әрбір сынауда 0,002 тең
болса, онда А оқиғасы 1000 сынауда 3 рет пайда болу ықтималдығын табу үшін қандай формулаға саласыз: Пуассон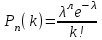 немесе Бернулли теңдеуі
немесе Бернулли теңдеуі
#5
*!Сапасыз өнімді шығару ықтималдығы 0,02. Шығарылған 2500 өнімнің ішінде 50 өнімнің сапасыз болу ықтималдығы табу үшін, қандай формулаға саласыз: Пуассон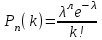
#6
*! Лапластың интегралдық формуласы:+++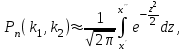
#7
*! Егер А оқиғасының пайда болу ықтималдығы әрбір сынауда 0,25 тең
болса, онда А оқиғасы 1000 сынауда 215ден 300ге дейін болу ықтималдығын табу үшін қандай формулаға саласыз: Лапластың интегралдық формуласы
Лапластың интегралдық формуласы
#8
*! Машинаның бір сағат ішінде жұмысшының назарын аудару ықтималдығы - 0,6 тең. Машиналардағы ақауларға байланысты, бір сағат ішінде жұмысшы өзі басқаратын төрт машинаның кез-келгенін талап етеді деген ықтималдығын табу үшін қандай формулаға саласыз: Байес формуласы
Байес формуласы
#9
*!Бернулли схемасында А оқиғасының ықтималдығы сынаудан сынауға дейін туындауы мүмкін ба?
#10
*!Жанұяда ұл баланың дүниеге келу ықтималдығы 0, 515. Қыз баланың туу ықтималдығы қандай? P=0,485
#11
*!Пуассон формуласы қандай жағдайларда қолданылады: Тәжірибелер саны n оқиғаның ықтималдығы p үлкен емес болған жағдайда ғана қолданылады.
#12
*!Лапластың локалдық формуласы қандай ықтималдықтарды есептейдi:
Сонымен, n тәуелсіз тәжірибеде А оқиғасы k рет пайда болу ықтималдығы, жуық түрде
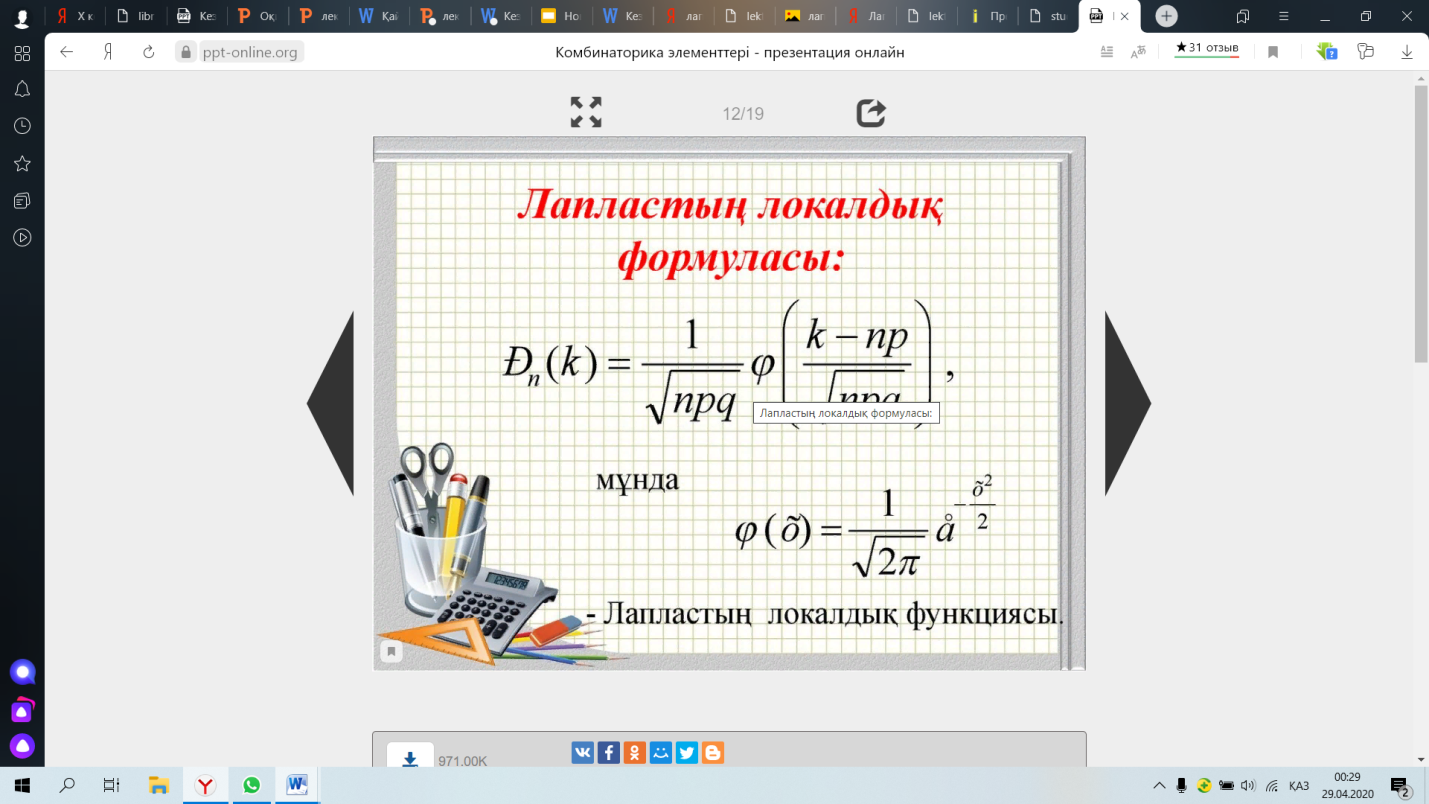
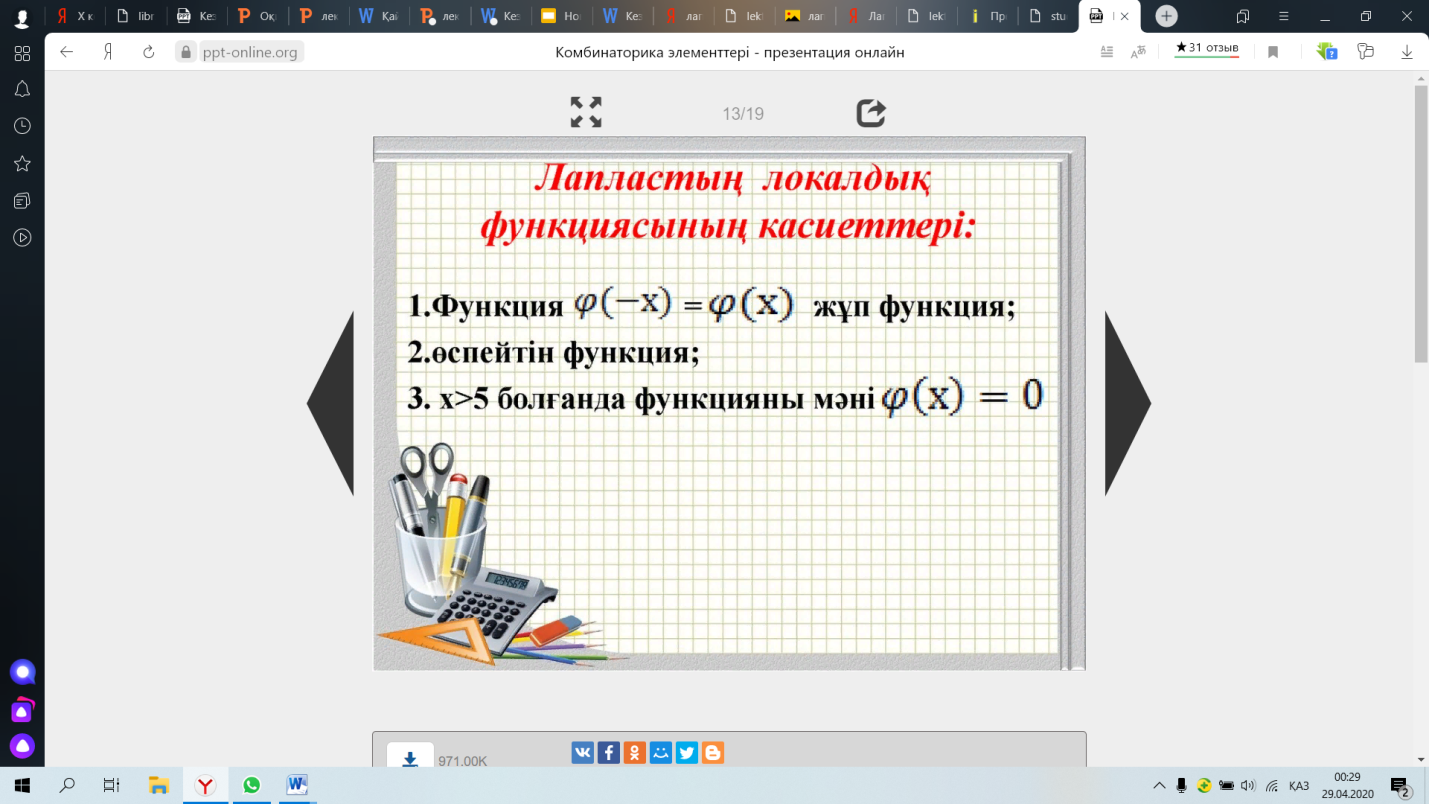
Сынаулар саны жеткiлiктi көп және оқиғаның пайда болу ықтималдығы қалыпты болған жағдайдағы оқиғаның n сынауда k рет пайда болу ықтималдығы
#13
*!Ойын сүйегі лақтырылды. Жұп сандар ұпайының түсу ықтималдығы қандай: 1/2
#14
*! Тиын 3 рет лақтырылды. 3 рет «герб» жағы түсуінің ықтималдығы: 0,125
#15
*! Тасымалдау кезінде ампуланың зақымдалу ықтималдығы p = 0,2 тең. Кездейсоқ таңдалған 400 ампуладан 70-тен 100 ампулаға дейін зақымдану ықтималдығын табыңыз.
0,88
#16
*!Муавр-Лапластың шектік формуласы: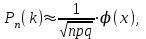 где
где 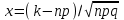 .
.
#17
*! Лапластың интегралдық функциясы:
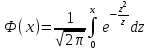 - Лапластың интегралдық функциясы.
- Лапластың интегралдық функциясы.
#18
*!Нысанаға 4 рет оқ атылды. Оқтың бiр рет атқандағы нысанаға тию ықтималдығы 0,25. Нысанаға бiрнеше рет атқандағы оқ тию ықтималдығын есептеу формуласын көрсетiңiз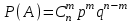 +
+
#19
*! Оқиғаның n сынаунәтижесiнде 1 ретпайдаболуықтималдығынесептеуформуласы
#4
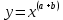 функциясының туындысы тең:*+
функциясының туындысы тең:*+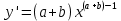
#5
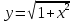 функциясының дифференциалы қай өрнекке сәйкес
функциясының дифференциалы қай өрнекке сәйкес#6 y = 2x3 - 5x2 + 7x + 4 функциясының туындысы неге тең? *+6x2-10x+7
#7 y = eax функцияның екінші ретті туындысы неге тең? *+a2eax
#8 !
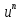 , мұндағы
, мұндағы  , функциясының туындысы тең *+шексіз аз
, функциясының туындысы тең *+шексіз аз#9 y =sin2x функциясының туындысы тең 2cos2x(Өзім жаздым тексеріп көр)
#10 y=(2x-3)3 функциясының екінші ретті дифференциалы қай өрнекке сәйкес*+24(2x-3) dx2
#11y = 5 x5 функциясының үшінші ретті туындысы: *+300 x2
#12 y = eax функциясының екінші ретті туындысы:+a2eax
#13 (2х-5)dx өрнегі ... функциясының дифференциалына сәйкес*+
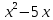
#14 y = 2x3 - 5x2 +7x +4 функциясының туындысы тең *+6x2-10x+7
1. Оқиға-қандай да бір сынау нәтижесінде пайда болатын кез-келген факт
2. Ықтималдықтың классикалық анықтамасы: қолайлы жағдайлар санының барлық мүмкін болатын жағдайлар санына қатынасы
3. Толық топ құрайтын екi үйлесiмсiз оқиға :*+қарама-қарсы
4. А және В –қарама-қарсы оқиғалары болса және Р(А)=1/6. Онда Р(В) тап: 5/6
4. Элементар оқиғалар кеңiстiгi: барлық мүмкін болатын элементар оқиғалар жиынтығы
5. А1, А2,…,Аn оқиғаларының кемiнде бiреуiнiң пайда болу ықтималдығы: P(A)=1-q1q2…qn
6. А және В оқиғаларының көбейтiндiсi : Осы оқиғалардың бірге пайда болуынан тұратын С оқиғасы
7. А және В оқиғаларының қосындысы: А оқиғасының немесе В оқиғасының пайда болуынан тұратын с оқиғасы
8. Тәуелсiз оқиғалардың бiрге пайда болу ықтималдығы: *+осы оқиғалардың ықтималдықтарының көбейтiндiсiне тең
9. Тәуелдi оқиғалардың бiрге пайда болу ықтималдығы : +бiр оқиға ықтималдығының екiншi оқиғаның шартты ықтималдығына көбейткенге тең
10. Сынау нәтижесiнде мiндеттi түрде пайда болатын оқиға : ақиқат
11. А оқиғасы толық топ құрайтын үйлесiмсiз В1, В2, …, Вn оқиғаларының бiрi орындалғанда ғана пайда болады. Бұл оқиғалардың қайсысы орындалатыны алдын ала белгiсiз болғандықтан, олар : жорамалдар
11. Кездейсоқ оқиғаның ықтималдығы: 0
11. Ақиқат оқиғаның ықтималдығы: 1
12. Р(А+В) символы ненi бiлдiредi? А немес В оқиғасының пайда болуының ықтималдығы
13. Толық ықтималдық формуласы++
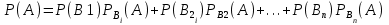
14. Байес формуласы +++
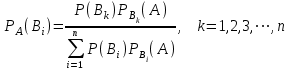
15. "Студент" сөзiнен сәтiне қарай бiр әрiп таңдалды. Таңдалынған әрiптiң дауысты болу ықтималдығы +
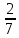
16. Жәшiкте 3қара, 5ақ, 4 қызыл шар бар. Сәтiнеқарайбiршаралынды. Алынған шардың қызыл емес болуының ықтималдығы неге тең.+ 2/3
17. Бiр жәшiкте 20 қорап анальгин, 50 қорап цитрамон және 30 қорап кофеин бар. Жәшiктен кездейсоқ қорап алынған. Алынған қораптың цитрамон немесе кофеин болу ықтималдығы 0,8
18. Жәшiкте 6 ақ, 4 қара шар бар. Кездейсоқ жәшiктен екi шар алынған. Алынған шардың екеуiнiң де ақ болу ықтималдығы 1/3
19. Екі мерген бір - біріне тәуелсіз нысанаға оқ атты. Бірінші мерген үшін нысанаға дәл тию ықтималдығы 0,7 –ге, екінші үшін 0,8-ге тең. Нысанаға дәл тию ықтималдығы 0,94
20. Екі мерген бір - біріне тәуелсіз нысанаға оқ атты. Бірінші мерген үшін нысанаға дәл тию ықтималдығы 0,7-ге тең, екінші мерген үшін 0,8-ге тең. Екі мергеннің бір мезгілде нысанаға дәл тию ықтималдығы +0,56
21. Екі мерген бір - біріне тәуелсіз нысанаға оқ атты. Бірінші мерген үшін нысанаға дәл тию ықтималдығы 0,7-ге тең, екінші мерген үшін 0,8-ге тең. Тек бір мергеннің нысанаға дәл тию ықтималдығы 0,38
22. Тұмау эпидемиясы кезінде ауруханаға жеткізілген 15 адамның ішіндегі 5-ң аяғы сынған. Палатаға 4 адамнан жатқызды. Жатқызылған адамдардың ішінде кем дегенде біреуінің аяғы сынған болып шығу ықтималдығы 11/13
23. Препараты стандарттылыққа екі фармацевттің бірімен тексеріледі. Препаратың бірінші фармацевтке түсу ықтималдығы 0,55, ал екінші фармацевтке – 0,45. Препаратты бірінші фармацевт стандартты деп қабылдау ықтималдығы 0,9, ал екінші фармацевт – 0,98. Препарат тексеру кезінде стандарты деп қабылданды. Бұл препаратты екінші фармацевт тексергендігінің ықтималдығын табыңыз 0,471
24. Әртүрлі перфораторда перфокарталардың бірдей жиынында екі перфораторшы берді. Бірінші перфораторшының қате жіберу ықтималдығы 0,05 тең, ал екінші перфораторшынікі 0,1 тең. Перфоратты тексеру кезінде қате табылуының ықтималдығын табыңыз 0,075
25. Бірдей формадағы 2 жәшік бар. 1-ші жәшікте 3 ақ, 2 қара, ал 2-ші жәшікте – 4 ақ және 3 қара шар бар. Кездейсоқ кез келген жәшіктен 1 шар алынады. Алынған шар ақ шар. Шар 1-ші жәшіктен алынғандығының ықтималдығын табыңыз. 0,59
26. Студент емтиханның 24 сұрағының тек 20–ын біледі. Бір билетте 3 сұрақ бар. Оған ең болмағанда бір дайындалмаған сұрағы бар билет түсу ықтималдығы 221/506
27. Жол апатында 12 адам зардап шекті, оның 4-і аяғын күйдіріп алды. Жедел жәрдем емханаға екі адамнан тасиды. Машинадағы екі адамның да аяғы күйген болып шығу ықтималдығы 1/11
28. Бөлімде 4 палата бар. Түнімен оттегі жастығын қажает ету ықтималдығы бірінші палата үшін – 0,2, екінші - 0,3, үшінші - 0,2, төртінші – 0,1. Түн ішінде екінші немесе үшінші палатаға оттегі жастығының қажет ету болып қалу ықтималдығы 0,5
кездейсоқ шамалар. 28 тест
#1
*! Х дискретті кездейсоқ шаманың математикалық күтімі төмендегі формула бойынша есептеледі +
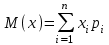
#2
*! Х және У тәуелсіз кездейсоқ шамалардың математикалық күтімдері мен дисперсиялары сәйкесінше М(Х)=2, D(X)=3, М(Y)=4, D(Y)=5 тең. Егер Z кездейсоқ шамасы Z=2X-Y+3 тең болса, М(Z) және D(Z) табыңыз:
+М(Z) = 3, D(Z)=4
#3
*! Тұрақты көбейткіш дисперсияның алдына D(CX)= +C^2D(x)
#4
*!Кездейсоқ шамалардың дисперсияларының қосындысы(айырымы) тең: +D(X+-Y)=D(x)+-D(y)
4.
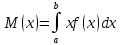 шамасы: үздіксіз кездейсоқ шаманың математикалық күтімі
шамасы: үздіксіз кездейсоқ шаманың математикалық күтімі#5
*!Дискретті кездейсоқ шама Х таралу заңдылығымен берілген. Р1 ықтималдығын табыңыз?
| X | 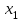 | 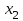 | 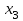 | 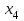 |
| Р | р1 | 0.2 | 0.1 | 0.5 |
0,2
#6
*!Дискретті кездейсоқ шама Х таралу заңдылығымен берілген.
| X | 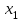 | 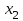 | 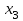 | 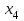 |
| Р | 0,2 | 0,1 | р3 | 0.4 |
р3 ықтималдығын табыңыз?
#7*! Тұрақты шаманың дисперсиясы тең …:D (С)=0
#8
*!Х кездейсоқ шамасын k тұрақты көбейткішке көбейткенде, оның математикалық күтімі қалай өзгереді: к-ға көбейтіледі
#9
*!Х кездейсоқ шамаға а саны қосылды. Осыдан оның дисперсиясы қалай өзгереді?
өзгермейді
#10
*!
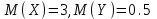 .
. 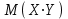 есептеңіз?1,5
есептеңіз?1,5#11
*!
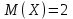 ,
,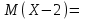 есептеңіз?-2
есептеңіз?-2#12
*!
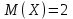 . М(2Х)= есептеңіз?4
. М(2Х)= есептеңіз?4#13
*!
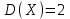 ,
, 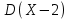 =есептеңіз?0
=есептеңіз?0#14
*!Х дискретті кездейсоқ шамасының таралу заңдылығы берілген, М(
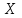 ) табыңыз
) табыңыз 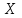 | –1 | 5 |
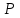 | 0.4 | 0.6 |
М(х)=2,6
#15
*!X және Y - тәуелсіз кездейсоқ шамалар,
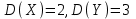 .
. 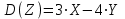 есептеңіз: Д=3*2-4*3=-6
есептеңіз: Д=3*2-4*3=-6#16
*!X және Y- тәуелсіз кездейсоқ шамалар,
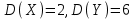 .
. 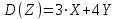 есептеңіз: D=3*2+4*6=6+24=30
есептеңіз: D=3*2+4*6=6+24=30#17
*!Х дискретті кездейсоқ шамасының таралу заңдылығы берілген, D(
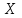 ) табыңыз.
) табыңыз. 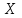 | 2 | 7 | 8 |
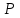 | 0.3 | 0,2 | 0.5 |
#18
*!
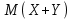 үшін формуласын табыңыз: M(X+Y)= M(X)+ M(Y)
үшін формуласын табыңыз: M(X+Y)= M(X)+ M(Y)#19
*!Х дискретті кездейсоқ шамасының дисперсиясының формуласы:
D(x)= M[x-M(x)]2
D(x)=M(x2)- [M(x)]2
#20
*! D (CX) үшін формуласын табыңыз:
D(CX)=C2D(x)
#21
*!D(X)=2, D(3X-1)= есептеңіз:2*3-1=5
#22
*!Таралу заңымен берілген, Х дискретті кездейсоқ шамасының математикалық күтімі неге тең:
| Х | 2 | 3 | 7 |
| Р | 0,1 | 0,4 | 0,5 |
#23
*! Дискретті кездейсоқ шама Х таралу заңдылығымен берілген. М(
 )=2,6. У табыңыз:
)=2,6. У табыңыз:  | –1 | y |
 | 0.4 | 0.6 |
#24
*! Дискретті кездейсоқ шама Х таралу заңдылығымен берілген. М(
 )=6,
)=6, табыңыз:
табыңыз:  |  | 7 | 8 |
 | 0.3 | 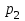 | 0.5 |
P2=0.2
#25
*! Дискретті кездейсоқ шама Х таралу заңдылығымен берілген. у есептеңіз:
 | –1 | 2 | 3 |
 | 0.2 | 0.5 | y |
#26
*! Х дискретті кездейсоқ шамасының дисперсиясы:
D(x)= M[x-M(x)]2
D(x)=M(x2)- [M(x)]2
#27
*! Дискретті кездейсоқ шама Х таралу заңдылығымен берілген. D(
 ) есептеңіз:
) есептеңіз: | X | -2 | -1 | 0 | 1 |
| р | 1/4 | 1/4 | 1/4 | 1/4 |
#28
*!Дискретті кездейсоқ шама Х таралу заңдылығымен берілген. М(
 ) есептеңіз:
) есептеңіз:  | -2 | -1 | 0 | 1 |
| р | 1/4 | 1/4 | 1/4 | 1/4 |
Қайталанбалы сынаулар. 56 тест
#1
*! Бернулли формуласы: Pn(K)=Cknpkqn-k
тендеуі:
#2
*! Лапластың интегралдық формуласы қандай ықтималдықтарды есептейдi:+оқиғаның n сынауда k1-ден k2-ге дейiн пайда болуын.
# 3. Егер А оқиғасының пайда болу ықтималдығы әрбір сынауда 0,25 тең
болса, онда А оқиғасы 1000 сынауда 250ден 300ге дейін болу ықтималдығын табу үшін қандай формулаға саласыз: Муавр-Лаплас
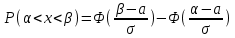 немесе Лапластың интегралдық формуласы
немесе Лапластың интегралдық формуласы#4
*! Егер А оқиғасының пайда болу ықтималдығы әрбір сынауда 0,002 тең
болса, онда А оқиғасы 1000 сынауда 3 рет пайда болу ықтималдығын табу үшін қандай формулаға саласыз: Пуассон
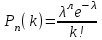 немесе Бернулли теңдеуі
немесе Бернулли теңдеуі#5
*!Сапасыз өнімді шығару ықтималдығы 0,02. Шығарылған 2500 өнімнің ішінде 50 өнімнің сапасыз болу ықтималдығы табу үшін, қандай формулаға саласыз: Пуассон
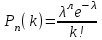
#6
*! Лапластың интегралдық формуласы:+++
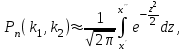
#7
*! Егер А оқиғасының пайда болу ықтималдығы әрбір сынауда 0,25 тең
болса, онда А оқиғасы 1000 сынауда 215ден 300ге дейін болу ықтималдығын табу үшін қандай формулаға саласыз:
 Лапластың интегралдық формуласы
Лапластың интегралдық формуласы#8
*! Машинаның бір сағат ішінде жұмысшының назарын аудару ықтималдығы - 0,6 тең. Машиналардағы ақауларға байланысты, бір сағат ішінде жұмысшы өзі басқаратын төрт машинаның кез-келгенін талап етеді деген ықтималдығын табу үшін қандай формулаға саласыз:
 Байес формуласы
Байес формуласы#9
*!Бернулли схемасында А оқиғасының ықтималдығы сынаудан сынауға дейін туындауы мүмкін ба?
#10
*!Жанұяда ұл баланың дүниеге келу ықтималдығы 0, 515. Қыз баланың туу ықтималдығы қандай? P=0,485
#11
*!Пуассон формуласы қандай жағдайларда қолданылады: Тәжірибелер саны n оқиғаның ықтималдығы p үлкен емес болған жағдайда ғана қолданылады.
#12
*!Лапластың локалдық формуласы қандай ықтималдықтарды есептейдi:
Сонымен, n тәуелсіз тәжірибеде А оқиғасы k рет пайда болу ықтималдығы, жуық түрде


Сынаулар саны жеткiлiктi көп және оқиғаның пайда болу ықтималдығы қалыпты болған жағдайдағы оқиғаның n сынауда k рет пайда болу ықтималдығы
#13
*!Ойын сүйегі лақтырылды. Жұп сандар ұпайының түсу ықтималдығы қандай: 1/2
#14
*! Тиын 3 рет лақтырылды. 3 рет «герб» жағы түсуінің ықтималдығы: 0,125
#15
*! Тасымалдау кезінде ампуланың зақымдалу ықтималдығы p = 0,2 тең. Кездейсоқ таңдалған 400 ампуладан 70-тен 100 ампулаға дейін зақымдану ықтималдығын табыңыз.
0,88
#16
*!Муавр-Лапластың шектік формуласы:
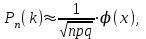 где
где 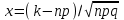 .
.#17
*! Лапластың интегралдық функциясы:
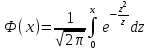 - Лапластың интегралдық функциясы.
- Лапластың интегралдық функциясы.#18
*!Нысанаға 4 рет оқ атылды. Оқтың бiр рет атқандағы нысанаға тию ықтималдығы 0,25. Нысанаға бiрнеше рет атқандағы оқ тию ықтималдығын есептеу формуласын көрсетiңiз
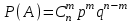 +
+#19
*! Оқиғаның n сынаунәтижесiнде 1 ретпайдаболуықтималдығынесептеуформуласы