Сенің қолыңнан бәрі келеді, тек өзіңе сен

(кейбір сұрақтардың жауабын таба алмадым, барымша істедім)

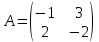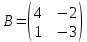#1. және матрицалары берілген. C=A+Bматрицасының c₁₂ элементі: 1

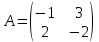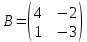#2. және матрицалары берілген. C=A*B матрицасының c₁₂ элементі: -7 дұрыс жауабы жоқ

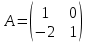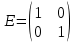#3. және матрицалары берілген.D=2A-Eматрицасы:

2A=2* =

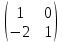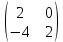
D=2A-E = - =

+

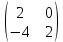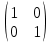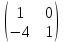
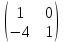
#4. С=АВөлшемі, егер А(2×3), В(3×2) болса

Бірінші матрицаның баған саны мен екіншісінің жолына тең

(2*2)

#5. Берілген А квадрат матрицасының а₃₂ элементінің М₃₂ миноры келесі жол мен бағандарды сызып тастағаннан алынады …: 3 жол мен 2 бағанды

5. Диагональ матрицаның бас диагоналі тек 1 тұратын матрица: бірлік матрица

#6

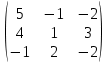*! матрицасының а₂₃ элементінің М₂₃ миноры

(-1)²⁺³ 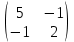( екінші жол, үшінші баған сызамыз)

#7. 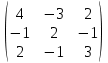матрицасының а₃₂ элементіне А₃₂ алгебралық толықтауышы

(-1)³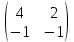⁺² * =-2

---

А₃₂=-6

#8. Егер А(m×l), В(n×k) болса, онда АВ матрицаларының көбейтіндісі үшін қойылатын шарт:

бағандар мен жолдар тең болу

#9. Екі матрица тең деп аталады, егер

олардың барлық сәйкес элементтері тең

#10. Қосу және азайту амалдары қандай матрицалар үшін орындалады:

Матрицалардың бірдей өлшемділігі: А=(a_ij) B=(b_ij)

#11. Анықтауышы нөлден өзгеше квадрат матрица

азғындалмаған

#12. 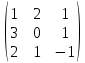матрицасының анықтауышының мәні

det A=0+3+4-0-1+6=12

#13. 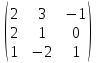матрицасының анықтауышының мәні

det A= 2+0+4+1-0-6=1

#14. 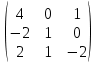матрицасының анықтауышының мәні

det A=-8-2+0-2-0-0=-12

#15. 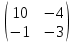матрицасының анықтауышының мәні

-30-4=-34

#16. Квадрат матрицаны транспонирлеген кезде оның анықтауышы

өзгермейді

#17. Матрицаның екі жолы немесе бағанының орындарын ауыстырса, онда оның анықтауышы

таңбасын қарама-қарсы таңбаға өзгертеді

#18. 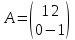матрицасына кері матрица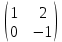

#19. 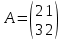матрицасына кері матрица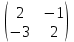

#20. А^-1 матрицасы А матрицасына кері деп аталады, егер:

A^(-1)*A=A*A^(-1)=E

#21. Кері матрица бар: матрица анықтауышы нөлден өзгеше болса

#22. А*A^-1 матрицаларының көбейтіндісі, мұндағы А^-1 – кері матрица:

A*A^(-1)=E Бірлік матрица

#23. Үшбұрыш матрица

Бас диагоналдан төмен орналасқан элементтері нөлге тең квадраттық матрица

*+

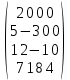
#24. Кері матрицаның есептелу тәсілі:



#25. Сызықты теңдеулер жүйесі тек келесі шарт орындалса ғана үйлесімді:

Егер жүйенің негізгі және кеңейтілген матрицаларының рангілері тең болса

#26. Кемінде бір шешімі бар жүйе: үйлесімді

*

---

Егер сызықтық теңдеулер жүйесі үйлесімді және жүйенің матрицасының рангісі белгісіздер санына тең болса

#27. Сызықты теңдеулер жүйесі біртекті деп аталады, егер

барлық бос мүшелері нөлге тең

#28. Егер теңдеулер жүйесі үйлесімді және оның бірден көп шешімі бар болса, онда ол: анықталмаған

#29. n – белгісіздер саны, m – жүйе теңдеулерінің саны. Крамер ережесінің қолданылуын қамтамасыз ететін шарт: m=n

#30. Егер сызықты теңдеулер жүйесінің шешімі болмаса, онда ол:

үйлесімсіз

#31. 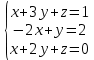теңдеулер жүйесі:Сызықты

#32. Жалғыз шешімі бар сызықты теңдеулер жүйесі: анықталған

#33. Бірден көп шешімі бар сызықты теңдеулер жүйесі: анықталмаған

#34. Егер теңдеулер жүйесі берілген жүйемен тең хұқылы болса, онда: жүйелердің шешімдері бірдей

#35.Егер жүйенің анықтауышы нөлге тең, ал белгісіздер коэффициенттерінің анықтауышы нөлге тең болмаса, жүйенің: шексіз көп шешімі бар

#36. Егер сызықты теңдеулер жүйесінің бір немесе бірнеше теңдеулерінде қандай да бір айнымалылар жоқ болса, онд:: анықтауышта оларға сәйкес элементтер нөлге тең!

#37. Теңдеулер жүйесін Гаусс әдісімен шешкен кезде болмайды

Егер сандарының кемінде біреуі нолден өзгеше болса

үйлесімділік

#38. «Гаусс әдісінің кері жолына» келесі амалды жатқызуға болады

Жүйе шешімдерін кері ретімен табу

белгісіздердің мәнін есептеу процесі

#39. Жүйенің шешімін анықтайтын Крамер формуласының жазылуы:



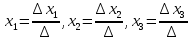
#40. 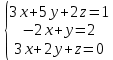жүйенің 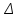анықтауышы:

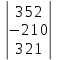=3-8+0-6-0+10= -1

#41. 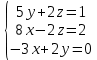жүйенің 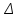_x анықтауышы

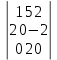* =0+8+0-0+4-0=12

---

#42. жүйенің _y анықтауышы

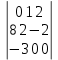. =0+0+6+12-0-0=18

#43. жүйенің _z анықтауышы

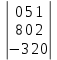* =0+16-30-0-0-0= -14

#44. 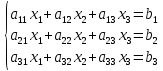сызықты теңдеулер жүйесінің бос коэффициенттерінің бағаны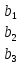

#45. 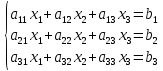сызықты теңдеулер жүйесінің белгісіздерінің бағаны: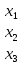

#46. 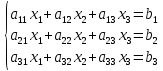сызықты теңдеулер жүйесінің анықтауышы :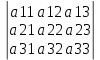

#47. 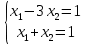теңдеулер жүйесінің шешімі: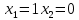

#48. 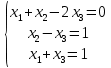теңдеулер жүйесінің шешімі: (0; 2; 1)

#49. 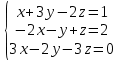теңдеулер жүйесінің шешімі: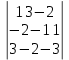

#50. 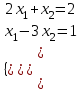теңдеулер жүйесінің шешімі: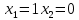
#51. 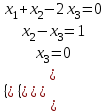теңдеулер жүйесінің шешімі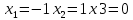


#52. 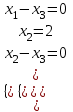теңдеулер жүйесінің шешімі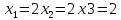


#53. 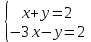теңдеулер жүйесін Крамер формулалары көмегімен шешіңіз. x-y есептеңіз:

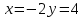-2-4=- 6

#54. 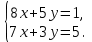теңдеулер жүйесін Крамер формулалары көмегімен шешіңіз.

---

x+y есептеңіз:-1
#55. 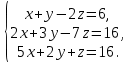теңдеулер жүйесінің шешімі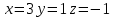



#56. Шексіз көп шешімі бар жүйе:

анықталмаған үйлесімді

#57. Жалғыз шешімі бар жүйе:

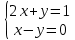
#58. 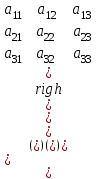матрицасының бас диагоналінің элементтері: a11a22a33

#59. 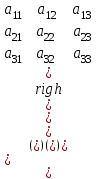матрицасының қосалқы диагоналінің элементтері: a31a22a13

#60.!n белгісізі бар n сызықты теңдеулер жүйесі:

#61. !n белгісізі бар n сызықты теңдеулер жүйесін шешу кезінде Крамер формулаларын қолдануға болады, егер …

#62. Сызықты теңдеулер жүйесі біртекті, егер

барлық бос мүшелері нөлге тең

#63. Сызықты теңдеулер жүйесі біртексіз, егер

бос мүшелер бағаны нөл емес

#64. 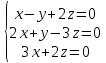біртекті теңдеулер жүйесінің шешімі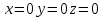



#65. Теңдеулер жүйесінің шешімі



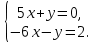
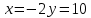
#66. Теңдеулер жүйесі берілген 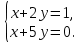Табу керек х+у

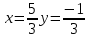5/3-3/1=4/3

#67. Теңдеулер жүйесі берілген 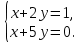Табу керек х-у

5/3+1/3=2

#68. Крамер формулалары



#69. !Сызықты теңдеулер жүйесін шешудің матрицалық әдісі:

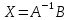
#70. Кері матрица әдісі – сызықты теңдеулер жүйесін шешудің ... әдісі

матрицалық

#71. Сызықты теңдеулер жүйесін шешудің матрицалық әдісі тек ... матрицалар үшін қолданылады

#72. 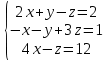теңдеулер жүйесінің шешімі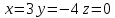



#73. Гаусс әдісімен 4 белгісізі бар 4 сызықты теңдеулер жүйесін шешу кезінде келесі матрица алынды

---

Смотрите также файлы

• Е. Е. Складнова, Г. А. Воробьёва ккоон.pdf

• Темы рефератов по дисциплине Социальная политика государства.docx

• Литература физика количество и доля сдававших егэ по предмету.docx

• Обобщающее повторение Дальний Восток Какой субъект рф не входит в состав Дальневосточного района.docx

• Тематическое планирование 2 класс 34 час Тематические блоки, темы Номер и тема урока Количество часов Основное содержание Методы и формы организации обучения.doc