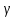= 1.67, для двухатомных газов (i = 5)

 = 1.4, для трёхатомных газов (i = 6) 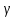= 1.33.

Тепловые машины. Цикл Карно

Тепловой машиной называется устройство, способное превращать полученное количество теплоты в механическую работу. Механическая работа в тепловых машинах производится в процессе расширения некоторого вещества, которое называется рабочим телом. В качестве рабочего тела обычно используются газообразные вещества (пары бензина, воздух, водяной пар). Рабочее тело получает (или отдает) тепловую энергию в процессе теплообмена с телами, имеющими большой запас внутренней энергии. Эти тела называются тепловыми резервуарами.

Реально существующие тепловые машины (паровые машины, двигатели внутреннего сгорания и т. д.) работают циклически. Процесс теплопередачи и преобразования полученного количества теплоты в работу периодически повторяется. Для этого рабочее тело должно совершать круговой процесс или термодинамический цикл, при котором периодически восстанавливается исходное состояние. Круговые процессы изображаются на диаграмме (p, V) газообразного рабочего тела с помощью замкнутых кривых.



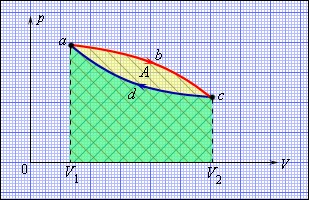
Рис. 5.1 Двухтактный термодинамический цикл.

При расширении газ совершает положительную работу 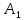, равную площади под кривой abc (жёлтая и зелёная области), при сжатии газ совершает отрицательную работу 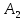, равную по модулю площади под кривой cda (только зелёная область). Полная работа за цикл 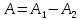на диаграмме (p, V) равна площади цикла (жёлтая область).

Общее свойство всех круговых процессов состоит в том, что их невозможно провести, приводя рабочее тело в тепловой контакт только с одним тепловым резервуаром. Их нужно, по крайней мере, два. Тепловой резервуар с более высокой температурой называют нагревателем, а с более низкой – холодильником. Совершая круговой процесс, рабочее тело получает от нагревателя некоторое количество теплоты

---

Q₁ > 0 и отдает холодильнику количество теплоты Q₂ < 0. Работа A, совершаемая рабочим телом за цикл, равна полученному за цикл количеству теплоты:

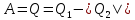(5.22)

Отношение работы A к количеству теплоты Q₁, полученному рабочим телом за цикл от нагревателя, называется коэффициентом полезного действия η тепловой машины:

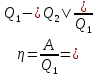(5.23)

Коэффициент полезного действия указывает, какая часть тепловой энергии, полученной рабочим телом от «горячего» теплового резервуара, превратилась в полезную работу. Остальная часть (1 – η) была «бесполезно» передана холодильнику. Коэффициент полезного действия тепловой машины всегда меньше единицы (η < 1).

В 1824 году французский инженер С. Карно рассмотрел круговой процесс, состоящий из двух изотерм и двух адиабат, который сыграл важную роль в развитии учения о тепловых процессах. Он называется циклом Карно



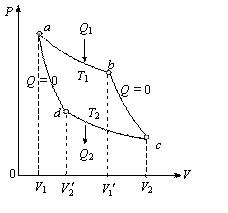
Рис. 5.2 Цикл Карно

Цикл Карно совершает газ, находящийся в цилиндре под поршнем. На изотермическом участке (a–b) газ приводится в тепловой контакт с горячим тепловым резервуаром (нагревателем), имеющим температуру T₁. Газ изотермически расширяется, совершая работу 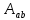, при этом к газу подводится некоторое количество теплоты 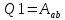. Далее на адиабатическом участке (b–c) газ помещается в адиабатическую оболочку и продолжает расширяться в отсутствие теплообмена. На этом участке газ совершает работу 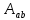>0. Температура газа при адиабатическом расширении падает до значения 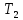. На следующем изотермическом участке (c–d) газ приводится в тепловой контакт с холодным тепловым резервуаром (холодильником) при температуре 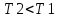. Происходит процесс изотермического сжатия. Газ совершает работу 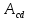< 0 и отдает тепло

---

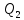< 0, равное произведенной работе . Внутренняя энергия газа не изменяется. Наконец, на последнем участке адиабатического сжатия газ вновь помещается в адиабатическую оболочку. При сжатии температура газа повышается до значения T₁, газ совершает работу 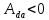. Полная работа A, совершаемая газом за цикл, равна сумме работ на отдельных участках:

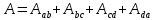(5.24)

На диаграмме (p, V) эта работа равна площади цикла. Особенность цикла Карно то, что можно выразить коэффициент полезного действия цикла через температуры нагревателя T₁ и холодильника T₂:

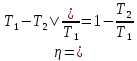(5.25)

Цикл Карно исключает теплообмен при конечной разности температур рабочего тела и окружающей среды (термостатов), когда тепло может передаваться без совершения работы. Поэтому цикл Карно – наиболее эффективный круговой процесс из всех возможных при заданных температурах нагревателя и холодильника. В термодинамике доказывается, что КПД цикла Карно является максимальным из всех возможных тепловых процессов в природе.

6.ЭЛЕКТРОМАГНЕТИЗМ

Магнитное поле – это силовое поле, которое действует на проводники с током и движущие заряды. Магнитное поле возникает возле проводников с током, движущихся зарядов и постоянных магнитов. Основные характеристики магнитного поля: 1) магнитная индукция 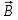; 2) напряженность магнитного поля 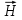; 3) магнитный поток Ф.

Магнитная индукция 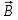– это векторная величина, которая выражает силовую характеристику магнитного поля. Она определяет с какой силой будет действовать магнитное поле на проводник с током или движущийся заряд. В системе СИ измеряется в теслах (Тл).

Принцип суперпозиции магнитных полей

Если имеется несколько источников магнитного поля, то магнитные индукции от каждого источника

---

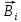
складываются по закону векторного сложения.

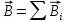(6.1^*)

Напряженность магнитного поля — это векторная величина, она связана с магнитной индукцией соотношением:

= µµ₀ (6.1)

где µ - магнитная проницаемость среды; µ₀ - магнитная постоянная. Напряженность магнитного поля в системе СИ измеряется в амперметр (А/м). В вакууме µ = 1, и тогда связь магнитной индукции ????⃗ с напряженностью магнитного поля задаётся соотношением: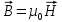

(6.2)

Магнитный поток Ф – это поток вектора магнитной индукция через произвольную поверхность S.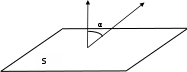



Рис. 6.1 Магнитный поток в однородном магнитном поле

В случае однородного магнитного поля и плоской поверхности магнитный поток задаётся формулой (Рис. 6.1):

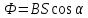или 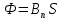, (6.3)

где S – площадь контура; α - угол между нормалью к плоскости контура и вектором магнитной индукции ; 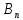– нормальная компонента вектора к поверхности S

В случае неоднородного поля и произвольной поверхности S магнитный поток задаётся формулой

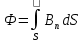, (6.4)

где ????_n – нормальная компонента вектора к поверхности S, а интегрирование ведется по всей поверхности S.

Закон Био – Савара – Лапласа. Для определения магнитной индукции

---

от элемента проводника d с током I в произвольной точке, определяемой радиусом-вектором используется закон Био – Савара – Лапласа (рис. 6.2)

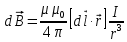, векторная форма (6.5)

или

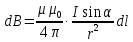, скалярная форма (6.5^*)

где 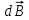– магнитная индукция поля, создаваемого элементом провода длиной 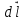с током I; – радиус-вектор, направленный от элемента проводника к точке, в которой определяется магнитная индукция; 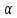- угол между радиусом-вектором и направлением тока в элементе провода.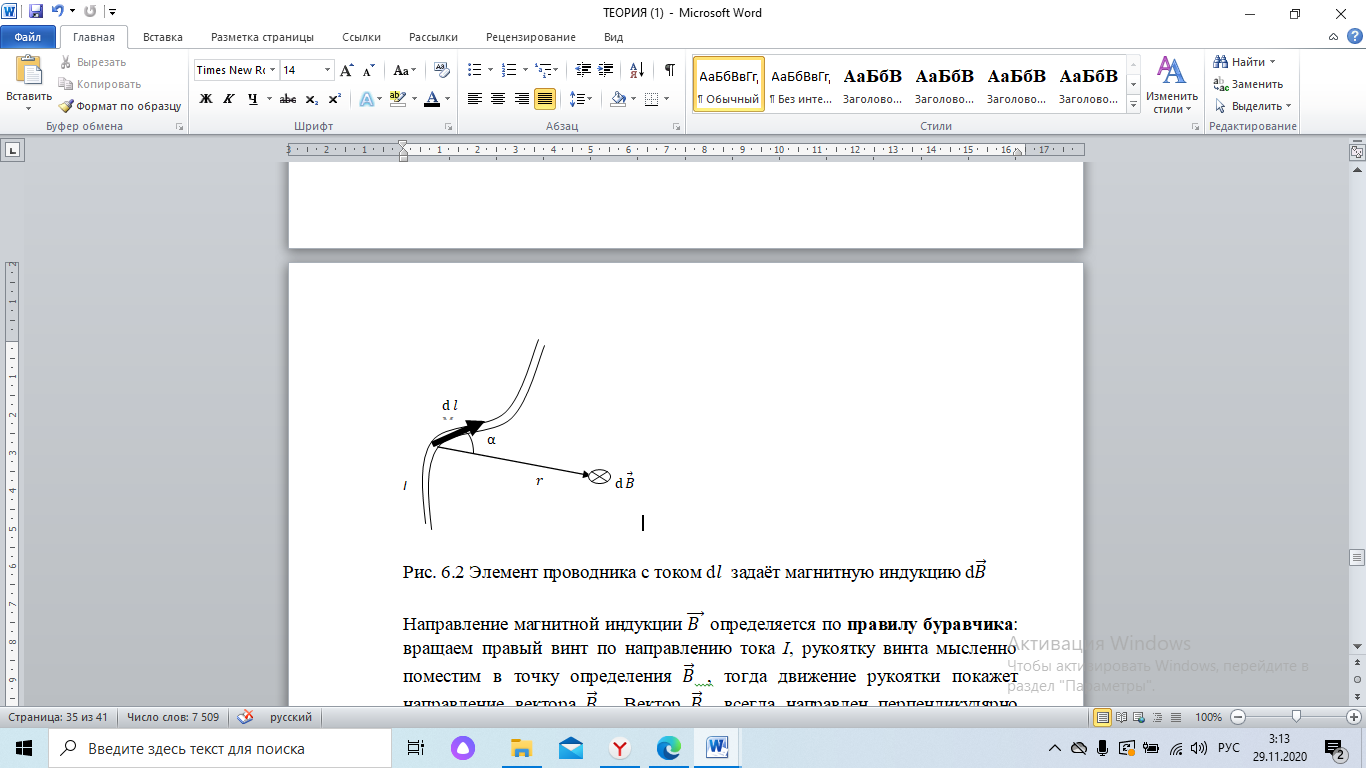


Рис. 6.2 Элемент проводника с током d???? задаёт магнитную индукцию d

Направление магнитной индукции определяется по правилу буравчика: вращаем правый винт по направлению тока I, рукоятку винта мысленно поместим в точку определения , тогда движение рукоятки покажет направление вектора . Вектор всегда направлен перпендикулярно плоскости, которую образуют вектора d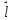 и .

Используя закон Био – Савара – Лапласа, можно рассчитать магнитную индукцию от различных конфигураций токов. Приведём примеры наиболее часто используемых конфигураций.

Магнитная индукция в центре кругового витка с током (Рис. 6.3)

---

Смотрите также файлы

• Задание 1 Определять сущность экономической безопасности как научной категории.docx

• Список педагогов мбоу сош 2 с. Самашки, прошедших кпк в 20202022 уч гг.docx

• Определите преимущества и недостатки использования стратегической ориентации на проектную форму организации и оплаты труда производственного персонала, заполнив для этого соответствующие графы таблицы.docx

• Халмуратов Азизбек Халмуратович москва 2023 Практическое занятие.docx

• Отчёт по статьям Статья 2.pdf