Файл: Кафедра физики расчётнографическая работа 1 Вариант 8 Мальцева Ю. Е. Группа зи221 Номер студенческого билета.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 145
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
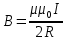 (6.6)
(6.6) где R – радиус кругового витка.
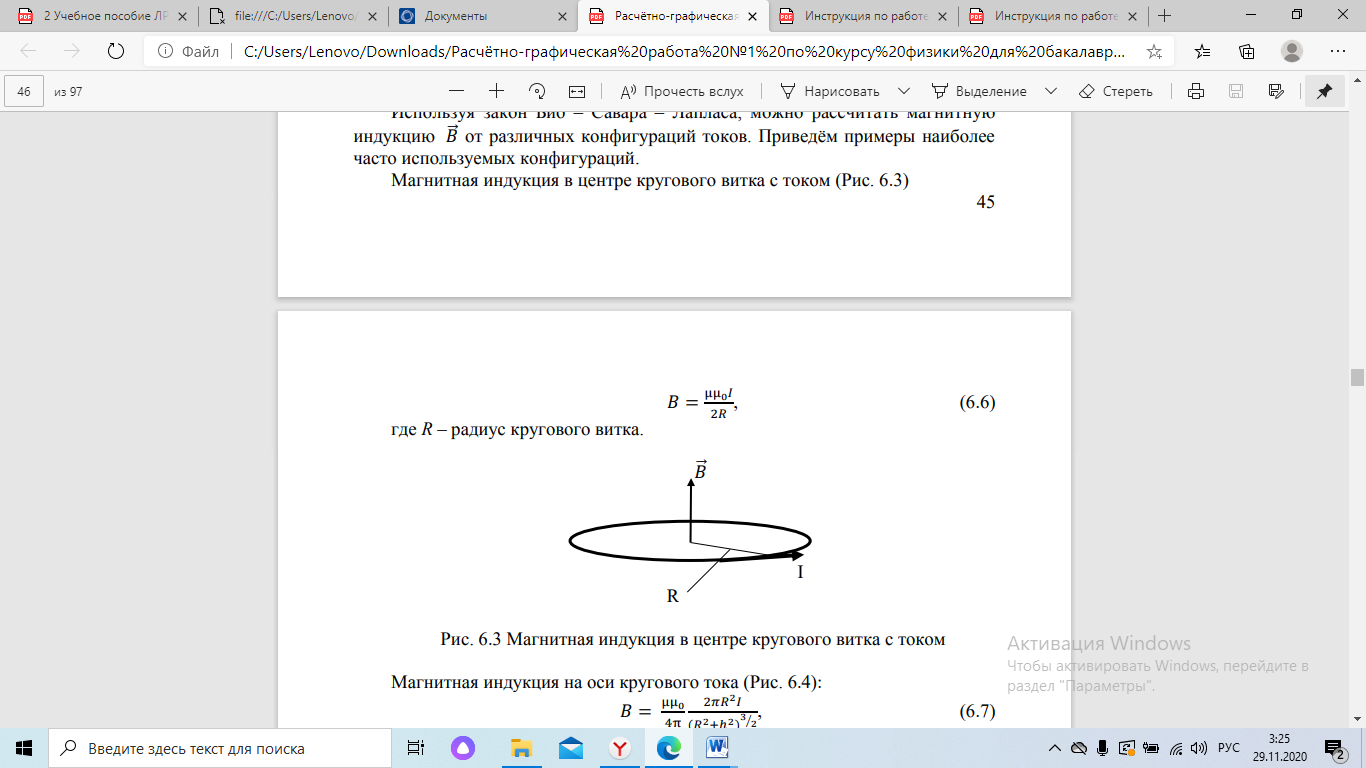
Рис. 6.3 Магнитная индукция в центре кругового витка с током
Магнитная индукция на оси кругового тока (Рис. 6.4):
????????2????
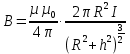 , (6.7)
, (6.7) где ℎ - расстояние от центра витка до точки, в которой определяется магнитная индукция.
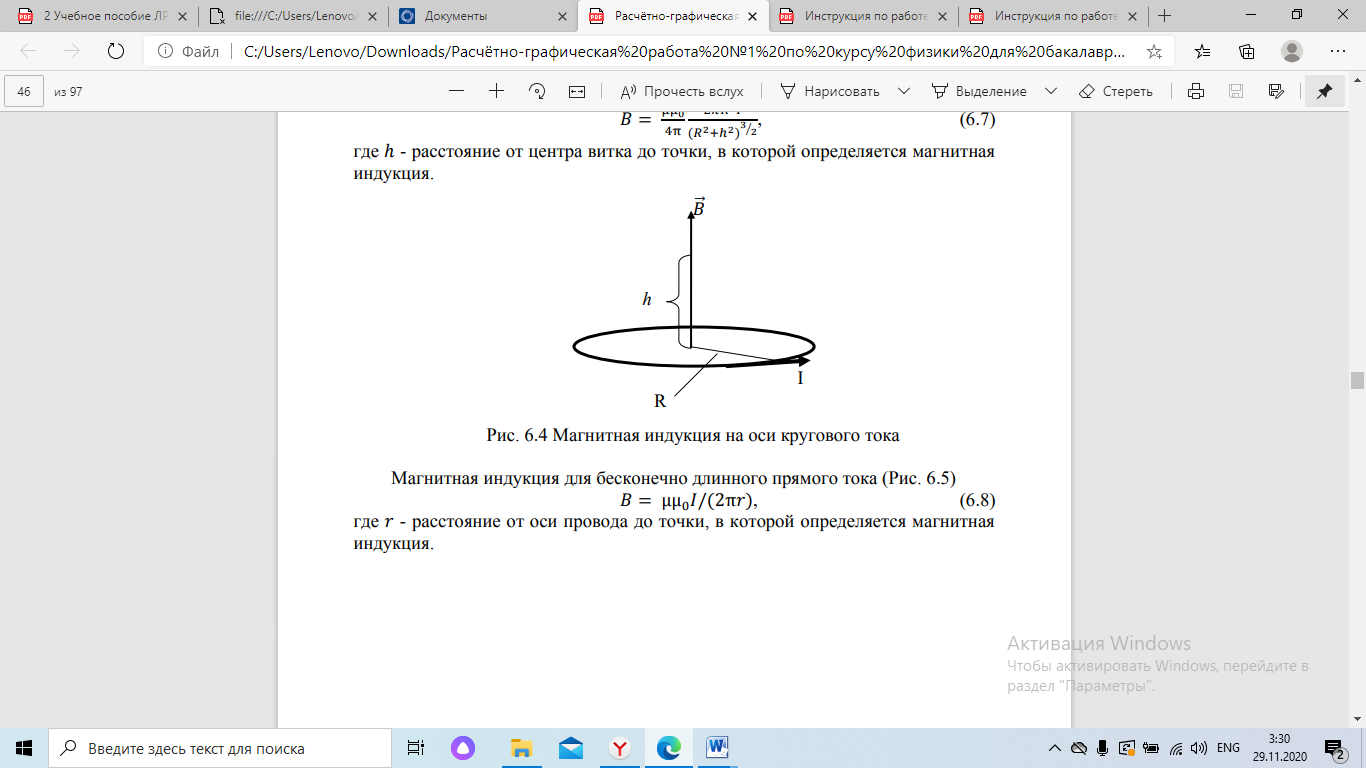
Рис. 6.4 Магнитная индукция на оси кругового тока
Магнитная индукция для бесконечно длинного прямого тока (Рис. 6.5)
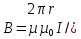 ), (6.8)
), (6.8) где ???? - расстояние от оси провода до точки, в которой определяется магнитная индукция.

Рис. 6.5 Магнитная индукция для бесконечно длинного прямого тока
Магнитная индукция, создаваемого отрезком провода с током (Рис.6.6),
???? =
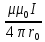 (cosα1 − cosα2). (6.9)
(cosα1 − cosα2). (6.9) 
Рис. 6.6 Магнитная индукция, создаваемого отрезком провода с током
где α1 – угол между проводником и радиусом-вектором, проведённым в точку определения
 ; α2 - угол между продолжением проводника и радиусом вектором, проведённым в точку определения
; α2 - угол между продолжением проводника и радиусом вектором, проведённым в точку определения  . Направление вектора магнитной индукции
. Направление вектора магнитной индукции  обозначено кружочком с крестиком – это значит, что
обозначено кружочком с крестиком – это значит, что  направлен перпендикулярно плоскости чертежа от нас в соответствии с правилом буравчика.
направлен перпендикулярно плоскости чертежа от нас в соответствии с правилом буравчика. Сила Лоренца
Сила Лоренца возникает в магнитном поле c индукцией ????⃗ и действует только на движущийся электрический заряд q:
 Л = ???? [
Л = ???? [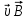 ], (6.10) или
], (6.10) или ????Л = ????????????sin????, (6.11)
где ???? – скорость заряженной частицы, α – угол между векторами
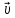 и
и  . Формула (6.10) определяет векторную форму, а (6.11) скалярную форму силы Лоренца.
. Формула (6.10) определяет векторную форму, а (6.11) скалярную форму силы Лоренца. Направление силы Лоренца определяется с помощью правила левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор
 , а четыре вытянутых пальца направить вдоль вектора ????, то отогнутый большой палец покажет направление силы, действующей на положительный заряд. На отрицательный заряд сила действует в противоположном направлении. Сила Ампера
, а четыре вытянутых пальца направить вдоль вектора ????, то отогнутый большой палец покажет направление силы, действующей на положительный заряд. На отрицательный заряд сила действует в противоположном направлении. Сила Ампера Сила Ампера
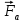 действует на прямолинейный проводник с током I, помещённый в магнитное поле c индукцией ????⃗ и определяется по формуле:
действует на прямолинейный проводник с током I, помещённый в магнитное поле c индукцией ????⃗ и определяется по формуле: 
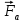 = ????[
= ????[
 ], (6.12)
], (6.12) или
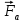 = ????????????sin????, (6.13)
= ????????????sin????, (6.13) где l – длина проводника, α – угол между векторами ???? и
 . Формула (6.12) определяет векторную форму, а (6.13) скалярную форму для силы Ампера.
. Формула (6.12) определяет векторную форму, а (6.13) скалярную форму для силы Ампера. Направление силы Ампера определяется с помощью правила левой руки:
если ладонь левой руки расположить так, чтобы в нее входил вектор
 , а четыре вытянутых пальца направить вдоль направления тока, то отогнутый большой палец покажет направление силы Ампера.
, а четыре вытянутых пальца направить вдоль направления тока, то отогнутый большой палец покажет направление силы Ампера. 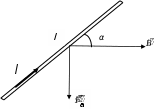
Рис. 6.7 Сила Ампера
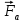
действует на проводник с током I помещённом в магнитное поле c индукцией

Электромагнитная индукция
Электромагнитной индукцией называется возникновение ЭДС ???????? в произвольном проводящем контуре, помещённом в переменное магнитное поле. ЭДС ???????? определяется по закону Фарадея:
???????? =
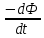 (6.14)
(6.14) где
 – производная от магнитный потока. Считается, что
– производная от магнитный потока. Считается, что 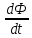 > 0 если магнитный поток возрастает,
> 0 если магнитный поток возрастает, 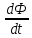 < 0 если магнитный поток уменьшается.
< 0 если магнитный поток уменьшается. Если контур замкнут, то в цепи протекает индукционный ток. Направление индукционного тока (а значит, и знака ЭДС индукции) определяется правилом Ленца: индукционный ток направлен так, чтобы противодействовать изменению магнитного потока. Если магнитный поток через контур увеличивается, то индукционный ток стремится уменьшить этот поток (знак минус в (6.14)), если магнитный поток через контур уменьшается, то индукционный ток стремится увеличить этот поток (знак минус в (6.14) меняется на плюс из-за отрицательного знака производной).
Сила индукционного тока, возникающего в контуре, определяется по закону Ома и закону электромагнитной индукции:
???? = -
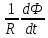 (6.15)
(6.15) где R – сопротивление контура.
Полный заряд q, протекающий в цепи в результате изменения магнитного потока ????.
Исходя из определения силы тока как скорости изменения заряда, количество электричества, прошедшего через поперечное сечение проводника при возникновении в нем индукционного тока равно: 1
???????? =
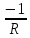 ????Φ, (6.16)
????Φ, (6.16) Тогда суммарный заряд ????, протекающий в цепи в результате изменения магнитного потока
q =
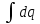 = -
= - 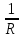
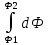 = -
= - (
(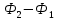 ) = -
) = -  (6.17)
(6.17) где
Таким образом, полный заряд q, протекающий в цепи, в результате изменения магнитного потока Φ, равен отношению изменения магнитного потока в контуре ∆Φ к полному сопротивлению контура R.
Движение проводника в магнитном поле
Если проводник длиной l равномерно движется со скоростью ???? в магнитном поле с индукцией
 (Рис. 6.8), то на концах проводника возникает ЭДС индукции ????????:
(Рис. 6.8), то на концах проводника возникает ЭДС индукции ????????: ???????? = ????????????sin????, (6.18)
где ????−угол между
 и
и  .
. 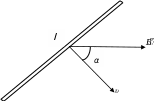
Рис. 6.8 Проводник длиной l равномерно движется со скоростью ???? в магнитном поле с индукцией
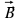
ЭДС индукции в контуре, который вращается в магнитном поле с постоянной угловой скоростью
ЭДС индукции, возникающая в контуре, имеющем число витков N, который вращается в магнитном поле с постоянной угловой скоростью ????, равна:
???????? = −????
 = ????????????sin????????, (6.19)
= ????????????sin????????, (6.19) где В – величина магнитной индукции, S – площадь контура, ???? – угловая скорость вращения контура.
Индуктивность проводника
Индуктивность проводника – это характеристика проводника, описывающая его способность препятствовать любому изменению силы тока в проводнике. Чем больше индуктивность, тем труднее изменить силу тока в проводнике.
Индуктивность произвольного проводника зависит от его формы и размеров, а также от свойств среды. Распространённым типом проводника в технической практике является соленоид – катушка с током. Это всевозможные контура, трансформаторы и т.п.
Индуктивность соленоида длиной l поперечным сечением S и числом витков N, равна:
???? = ????????0????2 ????⁄???? = ????????0????2????, (6.20)
где N - число витков в соленоиде; S – площадь поперечного сечения соленоида; ???? – длина соленоида; V – объём соленоида; ???? = ????⁄???? – плотность намотки (число витков на единицу длины). Индуктивность L измеряется в Генри (Гн).
Индуктивность в цепи постоянного тока
При включении индуктивности L в цепь постоянного тока с ЭДС ℰ (Рис. 6.9), обладающей сопротивлением R, мгновенное значение силы тока в цепи ????(????) будет меняться по закону:
????(????) =
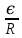 (1−????−????????⁄????) (при замыкании цепи), (6.21)
(1−????−????????⁄????) (при замыкании цепи), (6.21) где t – время, прошедшее после замыкания цепи;
????(????) = ????0????−????????⁄???? (при размыкании цепи), (6.22)
где ????0 - сила тока в цепи при t = 0; t – время, прошедшее с момента размыкания цепи.

Рис. 6.9 Индуктивность L в цепи постоянного тока с ЭДС
Энергия магнитного поля для замкнутого контура с индуктивностью L при протекании в цепи тока ???? определяется формулой:
???? =
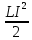 (6.23)
(6.23) Объемная плотность энергии магнитного поля (отношение энергии магнитного поля соленоида к его объему) определяется формулами:
???? = ????????⁄2, или ???? = ????2⁄2µµ0, или ???? = µµ0????2⁄2, (6.24)
где ???? - магнитная индукция; ???? - напряжённость магнитного поля.
7. КОЛЕБАНИЯ
ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
При изучении механических, световых, электромагнитных явлений мы наталкиваемcя на поразительную общность многих закономерностей. И появляется целесообразность изучения этих явлений с точки зрения выявления общих законов.
Когда мы говорим: качание маятника, звук «ЛЯ», желтый свет газовой горелки, электромагнитное поле лампового генератора, мы пользуемся языком акустики, оптики, радиофизики, на языке же общей для них физической теории – все это гармонические колебания, при которых значения физических величин меняются по закону синуса или косинуса.