Файл: Лабораторная работа 1 по теме Методы решения нелинейных уравнений.docx

5.5 Пример выполнения задания

2. 
   Задание для численного решения обыкновенных дифференциальных уравнений:
   

• 
  дифференциальное уравнение ;
  
• 
  интервал [0;1];
  
• 
  начальные условия x0=0, y0=1;
  
• 
  шаг интегрирования h0=0.1.
  

3. 
   Точное аналитическое решение заданного дифференциального уравнения
   

Найдем точное аналитическое решение заданного дифференциального уравнения (решение y=y(x))методом разделения переменных. Для этого запишем уравнение в виде и проинтегрируем с учетом начальных условий. Получим . Из начальных условий следует, что с=0.

Аналитическое решение дифференциального уравнения .

4. 
   Значения точного решения ОДУ –y(x)
   

Вычислим значения полученного решения y(xi) на отрезке [0;1] с шагом изменения аргумента h=0.1:

xi	y(xi)
0	1
0.1	1.1051711
0.2	1.2214026
0.3	1.3498585
0.4	1.4918243
0.5	1.6487202
0.6	1.8221179
0.7	2.0137515
0.8	2.2255394
0.9	2.4596014
1	2.7182798

5. 
   Численное решение заданного ДУ методом Эйлера
   

---

Найдем значения численного решение ОДУ методом Эйлера ( )в точках отрезка[0;1]с шагом h=0.1. Для этогоДУ записывают в виде y’=f(x,y) . Тогда общая формула для определения очередного значения функции по методу Эйлера имеет вид yi+1=yi+hf(xi,yi), где , :

xi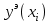
0
0.1	1.1000
0.2	1.210000
0.3	1.331000
0.4	1.4641001
0.5	1.6105101
0.6	1.7715611
0.7	1.9487172
0.8	2.1435795
0.9	2.3579478
1	2.5937426

6. 
   Значения погрешностей
   
7. 
   Вычислим значения погрешностей для , , :
   

   xi	Ei
   0
   0.1	0.005171
   0.2	0.011403
   0.3	0.018858
   0.4	0.027724
   0.5	0.038211
   0.6	0.050557
   0.7	0.065034
   0.8	0.081960
   0.9	0.101654
   1	0.124537

8. 
   Схема алгоритма и программа решения ОДУ методом Рунге-Кутты 4-го порядка с автоматическим выбором шага
   
9. 
   Схема алгоритма интегрирования ОДУ методом Рунге-Кутты 4-го порядка с автоматическим выбором шага приведена на рис.5.3-2 и рис. 5.3-3 в [2], а программу студенты должны написать самостоятельно.
   
10. 
    Решения, полученные по составленной программе «расчетом на ПК»
    
11. 
    Выполним программу и получим решение (то есть получим значения с шагом
    h= 0.1 и Е =10-4 ):
    

    xi
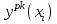
    0	1
    0.1	1.105171
    0.2	1.221403
    0.3	1.349859
    0.4	1.491825
    0.5	1.648721
    0.6	1.822119
    0.7	2.013753
    0.8	2.225541
    0.9	2.459603
    1	2.718282

12. 
    Значения погрешностей
    

---

Вычислим значения погрешностей ,

xi
0	0
0.1	0.0000001
0.2	0.0000004
0.3	0.0000005
0.4	0.0000007
0.5	0.0000008
0.6	0.0000011
0.7	0.0000015
0.8	0.0000016
0.9	0.0000016
1	0.0000022

Все решения, полученные выше, сведем в табл. результатов 1.5-2:

xi	y(xi)		Ei
0	1	1	0	1	0
0.1	1.1051711	1.1000	0.005171	1.105171	0.0000001
0.2	1.2214026	1.210000	0.011403	1.221403	0.0000004
0.3	1.3498585	1.331000	0.018858	1.349859	0.0000005
0.4	1.4918243	1.4641001	0.027724	1.491825	0.0000007
0.5	1.6487202	1.6105101	0.038211	1.648721	0.0000008
0.6	1.8221179	1.7715611	0.050557	1.822119	0.0000011
0.7	2.0137515	1.9487172	0.065034	2.013753	0.0000015
0.8	2.2255394	2.1435795	0.081960	2.225541	0.0000016
0.9	2.4596014	2.3579478	0.101654	2.459603	0.0000016
1	2.7182798	2.5937426	0.124537	2.718282	0.0000022

---

Где , ,

– аналитическое решение ОДУ,

- решение ОДУ, полученное методом Эйлера, ,

- решение ОДУ методом Рунге-Кутты 4-го порядка, .

13. 
    Графическая иллюстрация решений
    

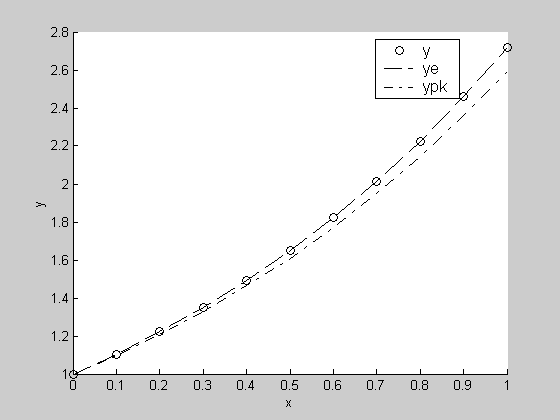
В данном случае решение y(x) совпадает с .

Контрольные вопросы по теме
Методы решения дифференциальных уравнений

1. 
   Что такое обыкновенное дифференциальное уравнение?
   
2. 
   Что такое порядок ОДУ?
   
3. 
   Что называется аналитическим решением ОДУ 1-го порядка?
   
4. 
   Что является общим решением ОДУ ?
   
5. 
   Что является геометрической интерпретацией общего решения ОДУ ?
   
6. 
   Что является численным решением ОДУ ?
   
7. 
   Что относится к начальным условиям при решении ОДУ 1-го порядка численными методами?
   
8. 
   По какому правилу проводят оценку погрешности решения методов Рунге-Кутты?
   
9. 
   Как выглядит формула для определения очередного значения функции по методу Рунге-Кутты 1-го порядка?
   
10. 
    Уменьшение шага интегрирования при использовании методов Рунге-Кутты приводит к уменьшению или увеличению погрешности?
    
11. 
    В обыкновенном дифференциальном уравнении присутствуют производные разных порядков от одной переменной или только первая производная от нескольких переменных?
    
12. 
    Методы Рунге-Кутты являются одношаговыми или многошаговыми методами?
    
13. 
    Сколько раз на каждом шаге необходимо вычислять в модифицированном методе Эйлера?
    
14. 
    Очередная точка решения ОДУ методом Рунге-Кутты вычисляется на основании одного или двух предыдущих значений функции?
    
15. 
    Возможно ли в методах Рунге-Кутты применение переменного шага интегрирования?
    
16. 
    Процесс решения дифференциального уравнения называется интегрированием или дифференцированием?
    
17. 
    Каковы формулы оценки погрешности методов Рунге-Кутты?
    
18. 
    Почему метод Эйлера называют методом Рунге-Кутты первого порядка?
    
19. 
    С помощью чего при оценке погрешности метода автоматического выбора шага учитывается порядок используемого метода Рунге-Кутты?
    
20. 
    Можно ли оценить погрешность решения ОДУ, не зная точного решения?
    

---

---