Файл: Ответы к экзамену комбинаторный признак умножения. Количество битовых строк длины.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 166
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Функциональное отношение f между элементами множеств А и В называетсяфункциейилиотображениемА в В, если 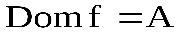 и обозначается
и обозначается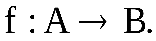
Множество А называется областью определения функции, множество В -областью значения функции.
Если y=f(x), то y называетсяобразомпри отображении f точки x, а x называетсяпрообразомпри отображении f точки y.
Пусть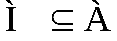 , тогда
, тогда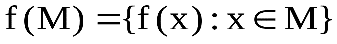 называетсяобразом множества (подмножества)М при отображении f. В частности,
называетсяобразом множества (подмножества)М при отображении f. В частности, 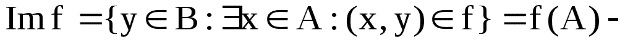 образ множества А при отображенииf.
образ множества А при отображенииf.
Пусть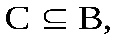 тогда
тогда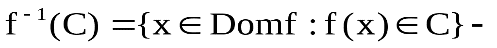 прообраз множества С при отображенииf. В частности,
прообраз множества С при отображенииf. В частности, 
Композиция
Определение1.Пусть f и g – функции, причем g: A→B, f: B→C.Композицией(суперпозицией, произведением) функций f и g называется отображение A в C, значением которого для произвольного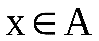 служитf(g(x)).
служитf(g(x)).
Обозначение: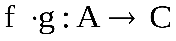 или
или 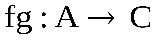 , то есть (fg)(x)=f(g(x)).
, то есть (fg)(x)=f(g(x)).
Определение2.Отображение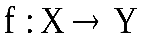
и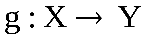 называется равными тогда и только тогда, когдаf(x)=g(x)
называется равными тогда и только тогда, когдаf(x)=g(x) 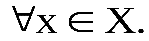
Пример:Пусть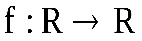 и
и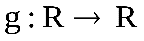 – функции, определяемые следующим образом:
– функции, определяемые следующим образом:
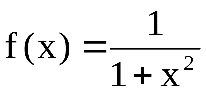 ; g(x)=1–x. Тогда
; g(x)=1–x. Тогда
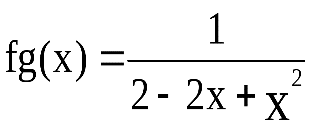 ;
; 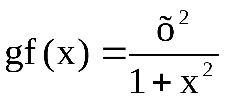
Из примера видно, что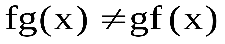 .
.
Теорема1:Пусть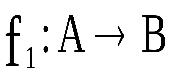 ,
,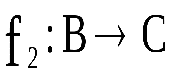 и
и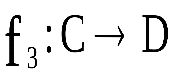 – отображения. Тогда
– отображения. Тогда 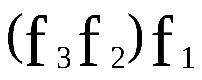 и
и 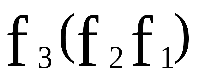 - отображенияA в D , причем
- отображенияA в D , причем 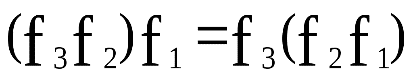 (1), то есть произведения отображений ассоциативно
(1), то есть произведения отображений ассоциативно
Доказательство.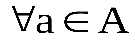 имеем:
имеем:
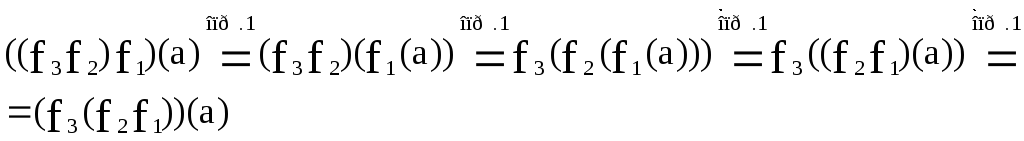
Следовательно, равенство (1) справедливо.
Что и требовалось доказать.
30. Биекция и перестановка. Обратная функция.
Бие́кция—отображение, которое является одновременно исюръективным, иинъективным. При биективном отображении каждому элементу одного множества соответствует ровно один элемент другого множества, при этом определено обратное отображение, которое обладает тем же свойством. Поэтому биективное отображение называют такжевзаимно однозначным отображением(соответствием).
Биективное отображение, являющеесягомоморфизмом, называютизоморфнымсоответствием.
Перестановкой из n элементов называется последовательность состоящая из всех элементов некоторого n-‘элементного множества причем число элементов этой последовательности равно n.
Обратной называется такая функция, для которой каждое ее значение (переменная y) определяется одним значением независимой переменной x из некоторого заданного множества X.
В алгебре принято следующее обозначение обратной функции:
Отметим, что не всякая функция является обратимой. Например, к квадратичной зависимости типаневозможно найти обратную функцию, так как два значения независимой переменной x задают одно значение переменной y.
Если теперь ограничить множество возможных значений аргумента интервалом, обратной функцией к исходной параболе станет функция видаСуществование обратной функции стало возможным, поскольку теперь аргумент может принимать только положительные значения.
Сформулируем необходимое условие обратимости функции.
К функции f(x) можно найти обратную тогда и только тогда, когда соблюдено каждое из представленных условий:
31. Числовые матрицы. Операции над матрицами.
Матрицей называется таблица чисел (выражений), имеющая m строк и n столбцов
Если матрица содержит 1 строку и n столбцов, то она называется матрицей-строкой
Если матрица содержит m строк и 1 столбец, то она называется матрицей-столбцом.
Матрица, у которой совпадает количество столбцов с количеством строк, называется квадратной.
Транспонированной к исходной квадратной матрице называется такая матрица, строки которой заменены на соответствующие столбцы, а столбцы - на соответствующие строки.
Матрицу, у которой все элементы, стоящие под главной диагональю равны нулю, будем называть треугольной
Матрица, все элементы которой равны нулю, за исключением элементов, стоящих на главной диагонали,
Суммой (разностью) двух матриц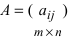 и
и 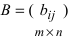 одинаковой структуры называется матрица той же размерности
одинаковой структуры называется матрица той же размерности 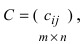 элементы которой вычисляются по формуле:
элементы которой вычисляются по формуле: 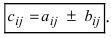

32. Матричное представление отношения. Булева матрица. Булевы операции над Булевыми матрицами.
Булевой матрицей (Boolean matrix) называется матрица, элементы которой принимают двоичные значения, т.е. 0 или 1.
Матрицей бинарного отношения P называется матрица ||P||=(pij) размерности n x m, где n=|A|, m=|B|
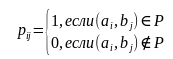
Если R являетсядвоичным отношениеммежду конечнымииндексированными наборами X и Y (так что R⊆X × Y), то R может быть представлен логической матрицей M, чьи индексы строки и столбца индексируют элементы X и Y соответственно, так что элементы M определяются как:
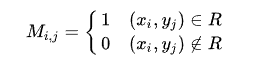
Множество А называется областью определения функции, множество В -областью значения функции.
Если y=f(x), то y называетсяобразомпри отображении f точки x, а x называетсяпрообразомпри отображении f точки y.
Пусть
Пусть
Композиция
Определение1.Пусть f и g – функции, причем g: A→B, f: B→C.Композицией(суперпозицией, произведением) функций f и g называется отображение A в C, значением которого для произвольного
Обозначение:
Определение2.Отображение
и
Пример:Пусть
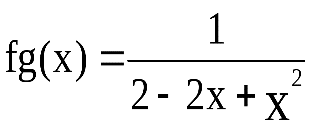 ;
; Из примера видно, что
Теорема1:Пусть
Доказательство.
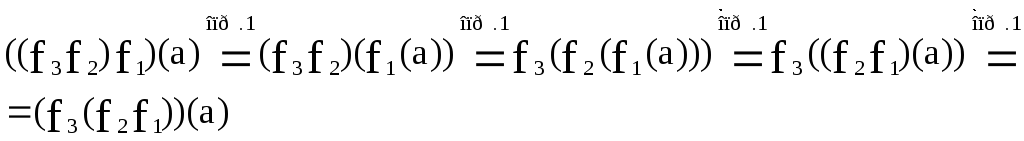
Следовательно, равенство (1) справедливо.
Что и требовалось доказать.
30. Биекция и перестановка. Обратная функция.
Бие́кция—отображение, которое является одновременно исюръективным, иинъективным. При биективном отображении каждому элементу одного множества соответствует ровно один элемент другого множества, при этом определено обратное отображение, которое обладает тем же свойством. Поэтому биективное отображение называют такжевзаимно однозначным отображением(соответствием).
Биективное отображение, являющеесягомоморфизмом, называютизоморфнымсоответствием.
Перестановкой из n элементов называется последовательность состоящая из всех элементов некоторого n-‘элементного множества причем число элементов этой последовательности равно n.
Обратной называется такая функция, для которой каждое ее значение (переменная y) определяется одним значением независимой переменной x из некоторого заданного множества X.
В алгебре принято следующее обозначение обратной функции:
Отметим, что не всякая функция является обратимой. Например, к квадратичной зависимости типаневозможно найти обратную функцию, так как два значения независимой переменной x задают одно значение переменной y.
Если теперь ограничить множество возможных значений аргумента интервалом, обратной функцией к исходной параболе станет функция видаСуществование обратной функции стало возможным, поскольку теперь аргумент может принимать только положительные значения.
Сформулируем необходимое условие обратимости функции.
К функции f(x) можно найти обратную тогда и только тогда, когда соблюдено каждое из представленных условий:
-
f(x)— непрерывно возрастающая или убывающая на заданной области допустимых значений X; -
одно значение переменной x задает только одно значение переменной y.
31. Числовые матрицы. Операции над матрицами.
Матрицей называется таблица чисел (выражений), имеющая m строк и n столбцов
Если матрица содержит 1 строку и n столбцов, то она называется матрицей-строкой
Если матрица содержит m строк и 1 столбец, то она называется матрицей-столбцом.
Матрица, у которой совпадает количество столбцов с количеством строк, называется квадратной.
Транспонированной к исходной квадратной матрице называется такая матрица, строки которой заменены на соответствующие столбцы, а столбцы - на соответствующие строки.
Матрицу, у которой все элементы, стоящие под главной диагональю равны нулю, будем называть треугольной
Матрица, все элементы которой равны нулю, за исключением элементов, стоящих на главной диагонали,
Суммой (разностью) двух матриц

32. Матричное представление отношения. Булева матрица. Булевы операции над Булевыми матрицами.
Булевой матрицей (Boolean matrix) называется матрица, элементы которой принимают двоичные значения, т.е. 0 или 1.
Матрицей бинарного отношения P называется матрица ||P||=(pij) размерности n x m, где n=|A|, m=|B|
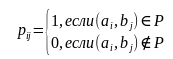
Если R являетсядвоичным отношениеммежду конечнымииндексированными наборами X и Y (так что R⊆X × Y), то R может быть представлен логической матрицей M, чьи индексы строки и столбца индексируют элементы X и Y соответственно, так что элементы M определяются как: