ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 56
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
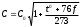(1) где
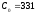м/с,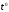 
- температура в градусах Цельсия, f- относительная влажность воздуха в значениях от 0 до 1. Линии положения (координаты x и y) и пересечение линий положения в искомой точке (координаты объекта) вычисляем, решая систему трех уравнений:
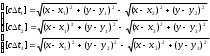, (2)Где
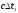- разность моментов прихода сигнала на 1 и 2 датчики;
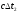- разность моментов прихода сигнала на 1 и 3 датчики;
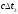- разность моментов прихода сигнала на 2 и 3 датчики;
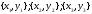- известные координаты 1,2 и 3 датчиков;x и y–вычисляемые координаты линий положения ; / .
Порядок выполнения работы:
-
Для заданного файла записи сигнала определить моменты прихода сигналов на датчики; -
Из приведенного примера выписать координаты X и Y трех датчиков; координаты объекта даны для проверки точности создаваемых линий положения. -
Зная моменты прихода сигналов на датчики найти три разности моментов прихода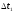
, 
, 
. -
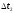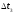Из файла метеопараметров 05_09.xls выписать температуру и влажность воздуха для заданного файла и, создав файл в пакете Excel, сосчитать скорость звука по формуле (1). -
Зная скорость звука, вычислить навигационные параметры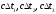
для каждой базы. -
Задавшись значениями x и y координат точки, лежащей на линии положения, рассчитать параметры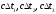 по формулам системы уравнений (2). Задача состоит в том, чтобы корректировать x и y таким образом, чтобы рассчитанные в системе уравнений параметры 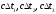совпали с параметрами, рассчитанными в п.5. Координаты x и y, полученные при этом, принадлежат точкам, лежащим на линиях равного положения, которые и необходимо построить. Для точности необходимо рассчитать 4 или 5 таких точек. -
Построить диаграмму в пакете Excel, на которой показать датчики, объект и линии положения, пересечение которых дает искомые координаты объекта, полученные с помощью сигналов датчиков.
Таблица 1 Расчёты моменты прихода сигналов на датчики и сравнение параметров С*∆t c навигационными параметрами
| XДатчики | X | Y | | | | | |
| 1 | 19052 | 58134 | | Температура | 12 | | |
| 2 | 18901 | 58447 | | Влажность | 0,64 | | |
| 3 | 18563 | 58524 | | C= | 338,485 | | |
| | | | | | | | |
| | | | | | | | |
Объект Датчики 1 2 3
Орудие 18612 58172 Время прихода 1,729 1,7301 1,7495
1---2 1---3 2---3
Точки Дельта T -0,0011 -0,0205 -0,0194
1----2 18001 57818 C*Дельта T -0,372333461 -6,938941776 -6,566608315
18250 57939
18550 58086 Вычисление 1---2 1---3 2---3
18900 58254 -0,539286274 -6,508098744 -6,631735964
1----3 18000 57294 -0,385193745 -6,73849365 -6,631307715
18245 57607 0,779917206 -6,801786925 -6,629765653
18550 57997 0,656904334 -6,777259084 -6,650394217
18900 58439
2----3 18000 54962
18245 56141
18550 57608
18900 59161
Таблица 2 8 вариант задания на выполнение работы
| Вариант 8 | t1=1,729 t2=1,7301 t3=1,7495 |
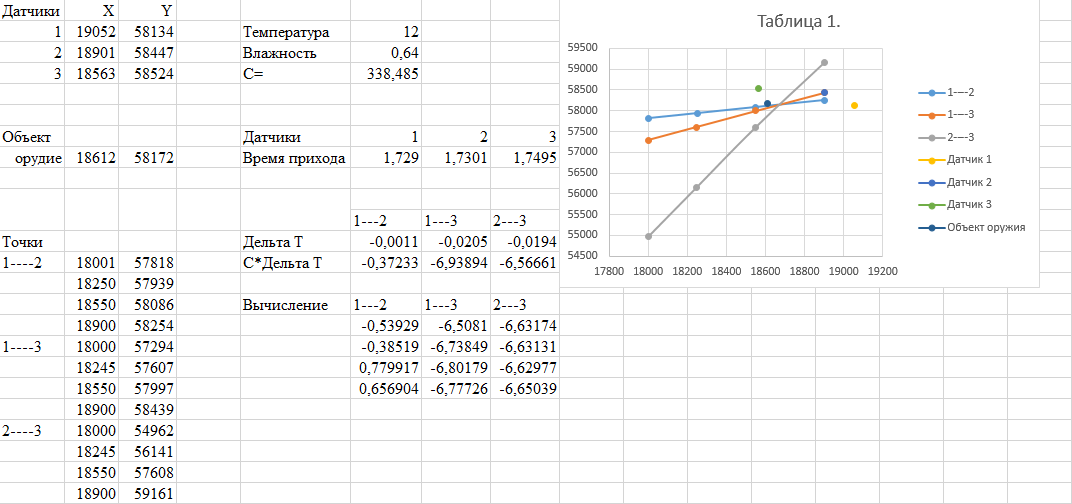
Рис. 1 Расчёты и таблица вычислений
Контрольные вопросы:
-
Опишите принцип определения местоположения объекта с помощью сигналов трех датчиков.
Ответ: Суть разностно-дальномерного метода заключается в определении местоположения источника сигнала путём измерения времени прихода сигнала в различные точки пространства. Для каждой такой точки (приёмника) сравнивается разность во времени прихода. Зная местоположение всех приёмников, можно найти местоположение источника сигнала. Этот принцип основан на использовании свойства гиперболы: разность расстояний
от любой точки гиперболы до дух определённых точек, называемых фокусами (гиперболе не принадлежат), есть величина постоянная. -
Опишите методику выполнения расчета.
Ответ: 1). Ищем моменты прихода сигналов на датчики (из заданного примера).
2). Из приведенного примера выписаны координаты X и Y трех датчиков; координаты объекта даны для проверки точности создаваемых линий положения.
3). Зная моменты прихода сигналов на датчики, находим три разности моментов прихода
, 
, 
.4). Находим скорость звука по формуле:
, где C0 = 331 м/c, а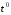 
и f– это заданные условия из файла 05_09.xls (Вариант S0021).5). Вычислены навигационные параметры для каждой базы, по формуле:
С * ∆t, где ∆t – разность времени прихода на датчики (1-2, 2-3, 1-3).
6). Рассчитываем параметры
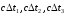по формулам системы: 
. Задача состоит в том, чтобы корректировать x и y таким образом, чтобы рассчитанные в системе уравнений параметры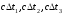 
совпали с параметрами, рассчитанными в п.5. Координаты x и y, полученные при этом, принадлежат точкам, лежащим на линиях равного положения, которые и необходимо построить. Для точности рассчитываем 4 или 5 таких точек.7). Строим диаграмму в пакете Excel, на которой есть: датчики, объекты и линии положения, пересечение которых даёт искомые координаты объекта, полученные с помощью сигналов датчиков.
Лабораторная работа № 7
Нелинейное программирование с помощью Excel
Цель работы: Понять, как работает нелинейное программирование в Excel.
Задание на выполнение работы: создать таблицы данных для размерности бака, таблицы «Отчет по устойчивости» самой таблицы данных и график с маркерами «Параметрирование по стоимости», с использованием программы Excel.
Порядок выполнения работы:
1. Ввод данных для задачи нелинейного программирования (размерности бака).
1.1 Создаём таблицу с переменными: длиной (а), шириной (b) и высотой (h) равных 1, а также в ячейке C8 и C9 вводим формулы по рис. 1, и получаем результаты (рис. 2).
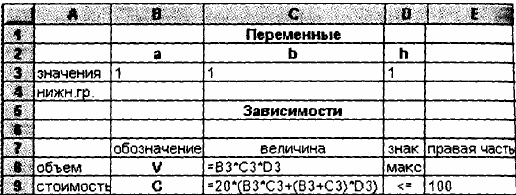
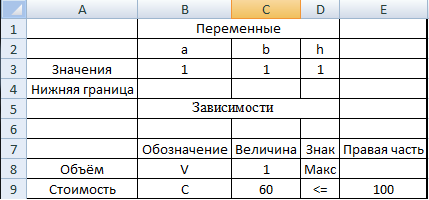
| Рис. 1 Таблица для расчёта объёма бака | Рис. 2 Готовая таблица |
1.2 Для того, чтобы работать с параметрами «Поиска решения», сначала заходим в вкладку «Данные», кликаем в «Поиск решения» (рис. 3).
Рис. 3 Значок «Поиска решения», диалогового окна
1.3 Заходим в диалоговое окно, оптимизируем целевую ячейку $С$8 (адрес величины объёма), вводим зависимость для целевой функции, которая максимизируется, потом добавляем значения переменных $B$3:$D$3 и пишем условия (рис. 4) в окно «Ограничения», с помощью кнопки «Добавить».
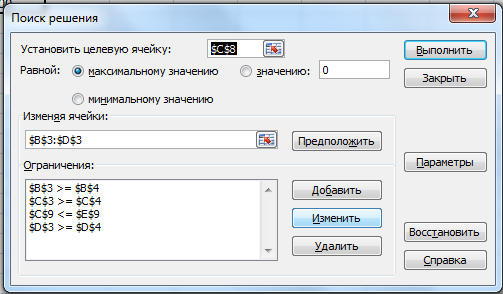
Рис. 4 «Поиск решения» с ограничениями
1.4 Вписываем все значения (рис. 5.1 и 5.2), нажав (рис. 4) кнопку «Параметры», после нажимаем «ОК», «Выполнить» и «ОК», изменятся значения в таблице (рис. 6).
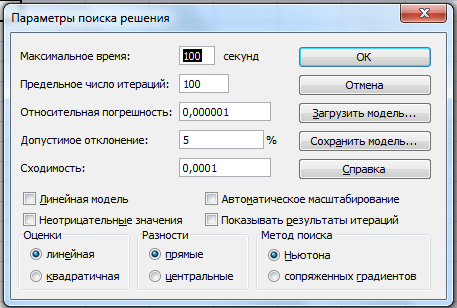
Рис. 5.1 «Параметры поиска решения», все её значения
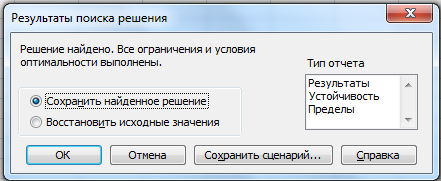
Рис. 5.2 «Результаты поиска решения»
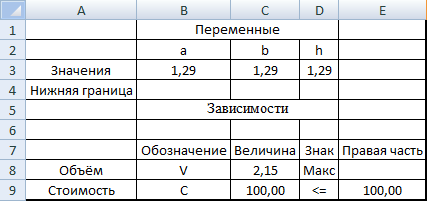
Рис. 6 Результат изменения таблицы по «Поиску решения»
2. Анализ оптимального решения
2.1 Нажав на «Устойчивость» (рис. 5.2), вызываем один вариант отчётов из трёх типов (рис. 7). На рис. 8 изображена сама таблица «Отчет по устойчивости».
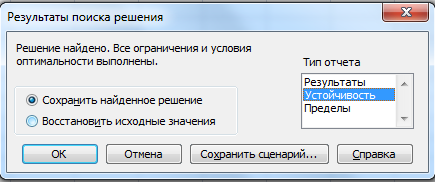
Рис. 7 «Устойчивость» в «Результатах поиска решения»
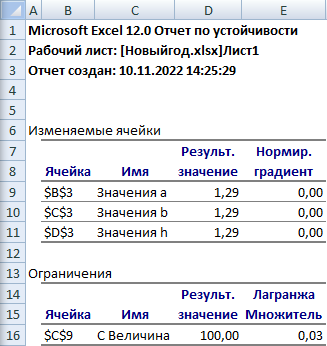
Рис. 8 Таблица «Отчет по устойчивости»
3. Вариантный анализ
3.1 Сначала в таблице (рис. 2) заменяем ячейку Е9 на различные значения (100 - 500). Потом заходим в «Поиск решения» (рис. 4), затем заходим в «Результаты поиска решения» и нажимаем на кнопку «Сохранить сценарий» (рис. 9), где мы вводим имя нового сценария, например, «С=100», и далее повторяем для каждого различного значения.