Файл: Введение Вычислительная мощность компьютера позволяет использовать его как средство автоматизации научной работы.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 56
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Выделение матрицы- мнимой части матрицы
K:=1..3
L:=1..3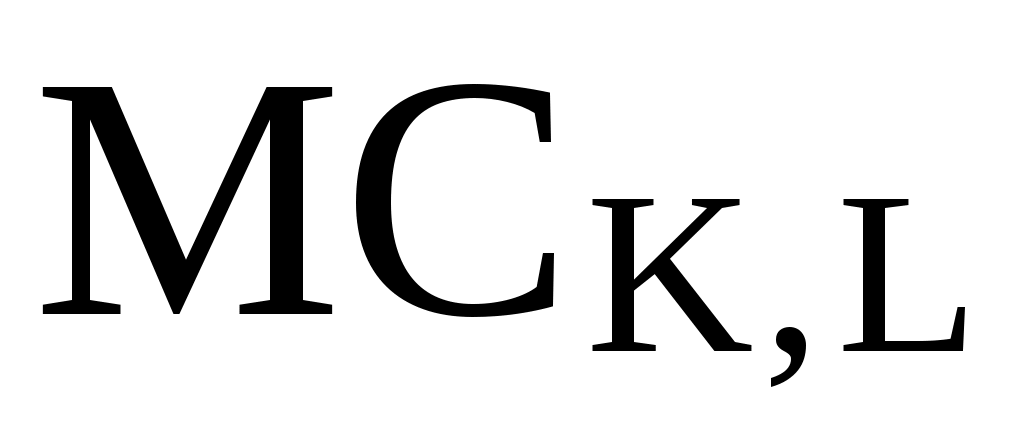
:=
+
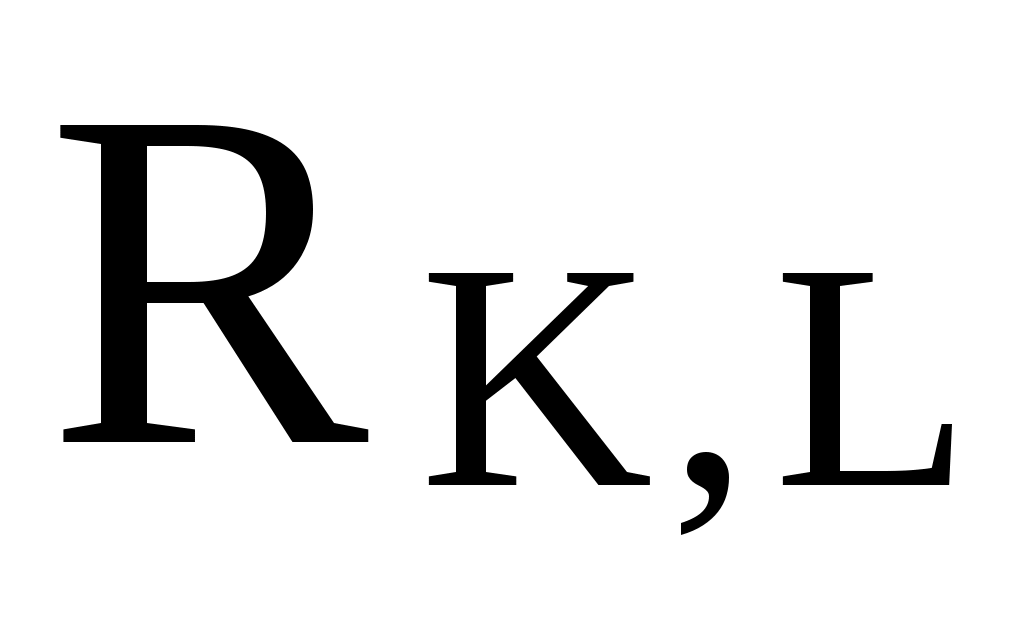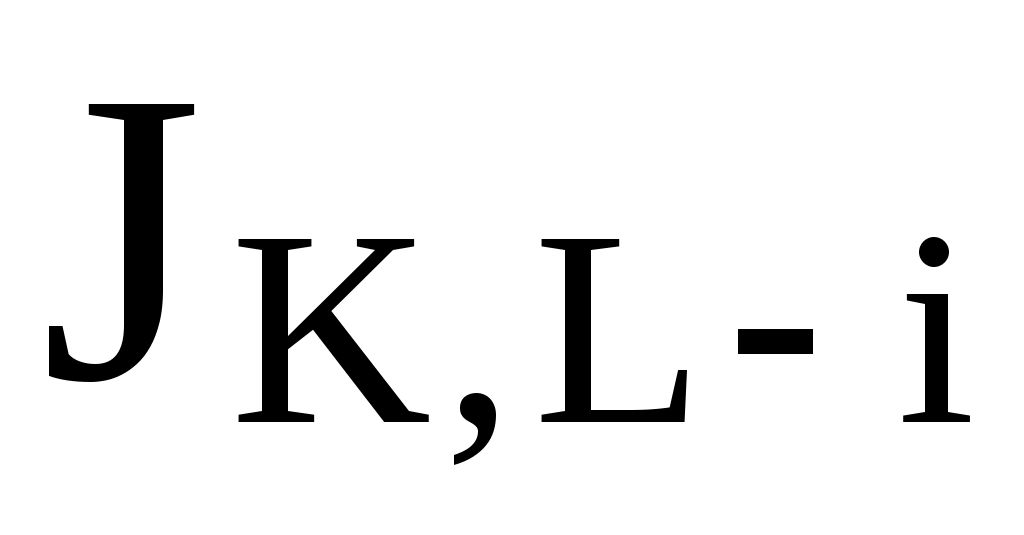Восстановление матрицы с комплексными элементами по матрицам R и J
МС=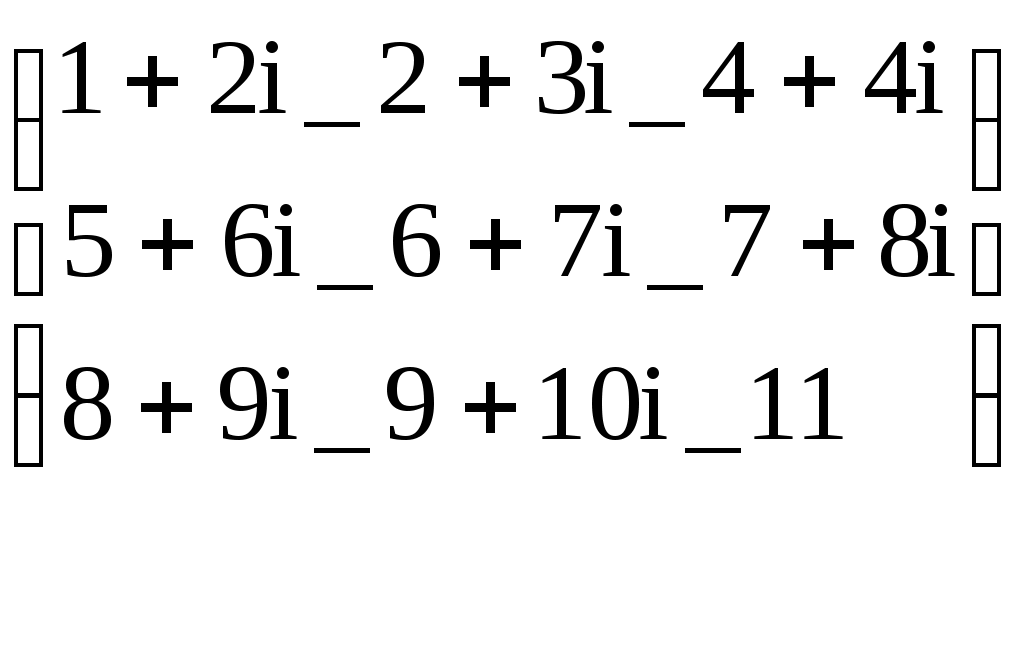
Вывод восстановленной матрицы ( МС=СМ)
3. Ранжированные переменные
До сих пор мы рассматривали переменные, которые имеют единственное значение. Однако в математике часто возникает необходимость в задании некоторого ряда значений – чаще всего упорядоченного. Например, для вычисления факториала N! = 12…(N-1)N нужно сформировать ряд чисел от 1 до N с шагом 1 и перемножить их. Также упорядоченный ряд значений какой-то переменной (например абсциссы x) нужен для построения графика функции – Mathcad строит графики функций по точкам, соединяя их по отрезкам прямых.
Для создания таких рядов в Mathcad используются так называемые ранжированные переменные. Иногда они заменяют управляющие структуры – циклы, однако полноценной такая замена всё же не является, в частности, потому что не предусмотрен выбор любого значения ранжированной переменной.
В самом простом случае для создания ранжированной переменной используется выражение: Name := Nbegin . . Nend, где Name – имя переменной, Nbegin – её начальное значение, Nend – конечное значение, .. – символ, указывающий на изменение переменной в заданных пределах (он вводится знаком точки с запятой ;). Если Nbegin < Nend, то шаг изменения переменной будет равен +1, в противном случае –1.
Для создания ранжированной переменной общего вида используется выражение: Name := Nbegin, (Nbegin + Step) . . Nend. Здесь Step – заданный шаг изменения переменной (он должен быть положительным, если Nbegin<Nend, или отрицательным в противном случае).
Примеры.
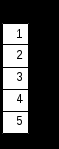
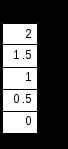
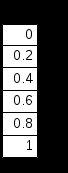
4. Построение графиков
Чтобы построить двумерный график в координатных осях X-Y, надо дать команду Insert – Graph – X-Y Plot (Вставка – График – Декартовые координаты). В области размещения графика находятся заполнители для указания отображаемых выражений и диапазона изменения величин. Заполнитель у середины оси координат предназначен для переменной или выражения, отображаемого по этой оси. Обычно используют ранжированную переменную или вектор значений. Граничные значения по осям выбираются автоматически в соответствии с диапазоном изменения величины, но их можно задать и вручную.
В одной графической области можно построить несколько графиков. Для этого надо у соответствующей оси перечислить несколько выражений через запятую.
Разные кривые изображаются разным цветом, а для форматирования графика надо дважды щелкнуть на области графика. Для управления отображением построенных линий служит вкладка Traces (Линии) в открывшемся диалоговом окне. Текущий формат каждой линии приведен в списке, а под списком расположены элементы управления, позволяющие изменять формат. Поле Legend Label (Описание) задает описание линии, которое отображается только при сбросе флажка Hide Legend (Скрыть описание). Список Symbol (символ) позволяет выбрать маркеры для отдельных точек, список Line (тип линии) задает тип линии, список Color (Цвет) – цвет. Список Type (Тип) определяет способ связи отдельных точек, а список Width (Толщина) – толщину линии.
Точно также можно построить и отформатировать график в полярных координатах. Для его построения надо дать команду Insert – Graph – Polar Plot (Вставка – График – Полярные координаты).
5. Решение уравнений и систем
Для численного поиска корней уравнения в программе MathCad используется функция root. Она служит для решения уравнений вида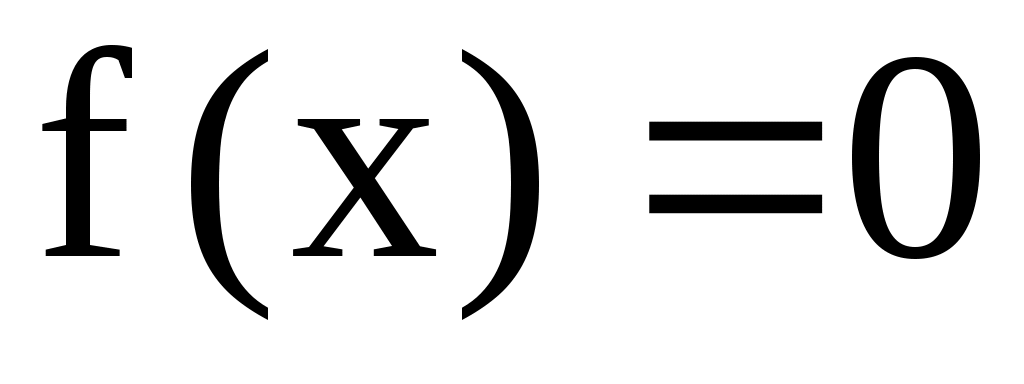
, где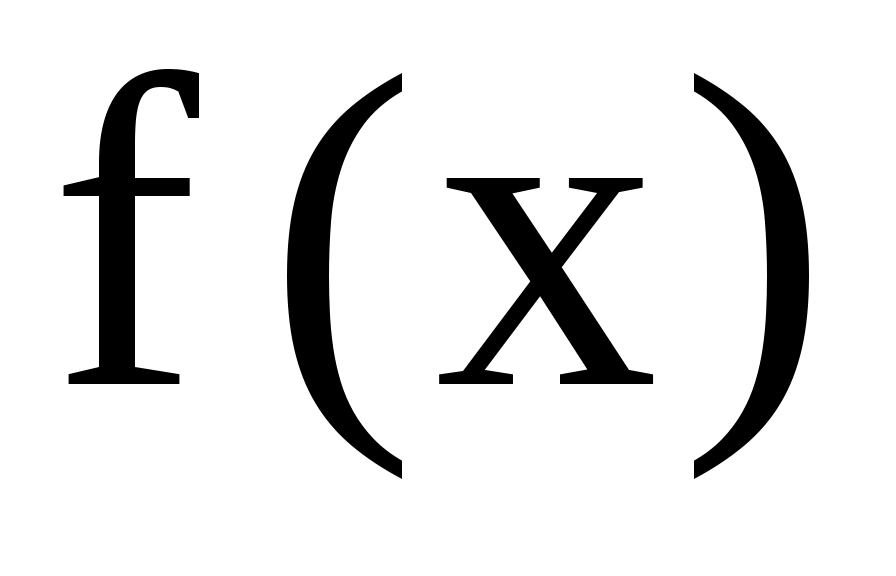
- выражение, корни которого нужно найти, а 
– неизвестное. Для поиска корней с помощью функции root, надо присвоить искомой переменной начальное значение, а затем вычислить корень при помощи вызова функции: 
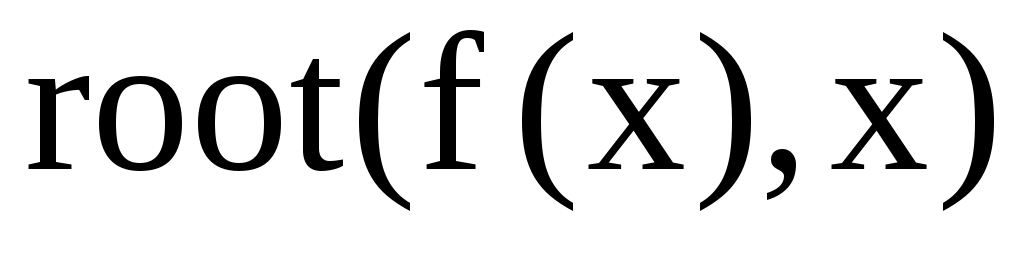. Здесь 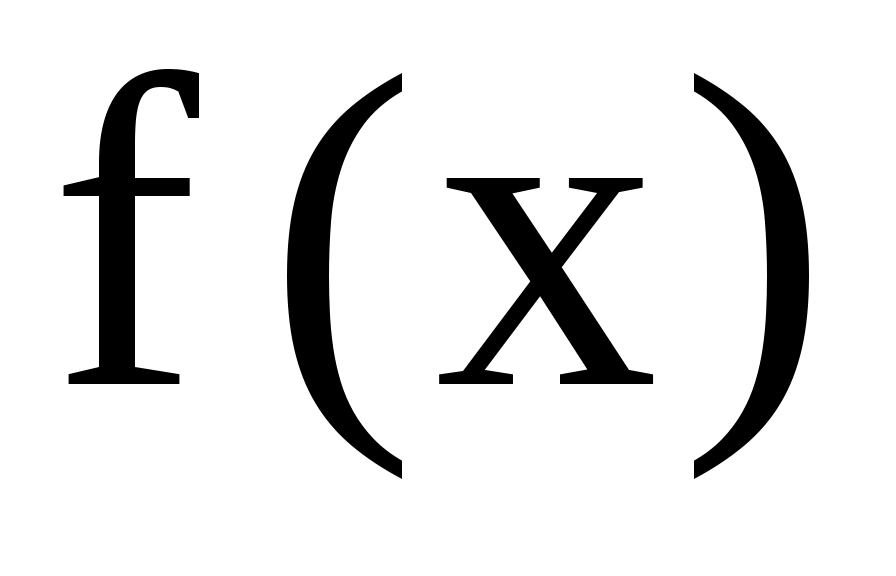- функция переменной , используемой в качестве второго параметра. Функция root возвращает значение независимой переменной, обращающее функцию 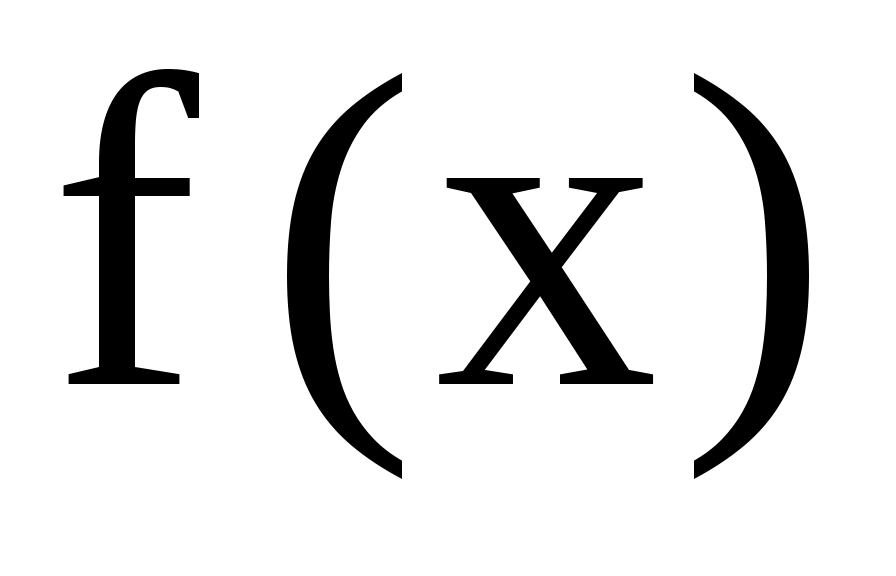в 0. Например:
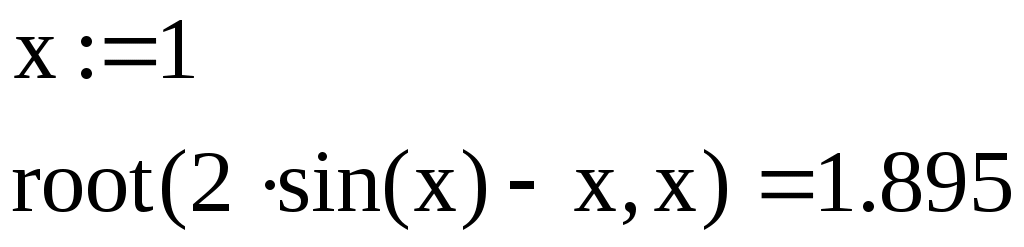
Если уравнение имеет несколько корней (как в данном примере), то результат, выдаваемый функцией root, зависит от выбранного начального приближения.
Если надо решить систему уравнений (неравенств), используют так называемый блок решения, который начинается с ключевого слова given (дано) и заканчивается вызовом find (найти). Между ними располагают логические выражения, задающие ограничения на значения искомых величин, иными словами, уравнения и неравенства. Всем переменным, используемым для обозначения неизвестных величин, должны быть заранее присвоены начальные значения.
Чтобы записать уравнение, в котором утверждается, что левая и правая части равны, используется знак логического равенства – кнопка Boolean Equals (Логически равно) на панели инструментов Evaluation (Вычисление). Другие знаки логических условий также можно найти на этой панели.
Заканчивается блок решения вызовом функции find, у которой в качестве аргументов должны быть перечисленные искомые величины. Эта функция возвращает вектор, содержащий вычисленные значения неизвестных. Например:
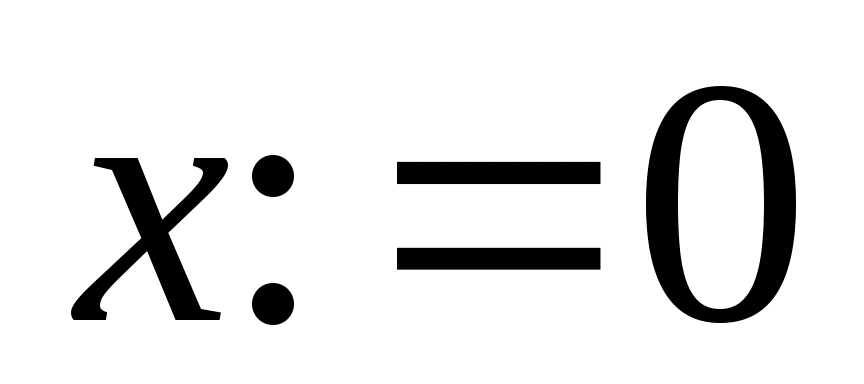
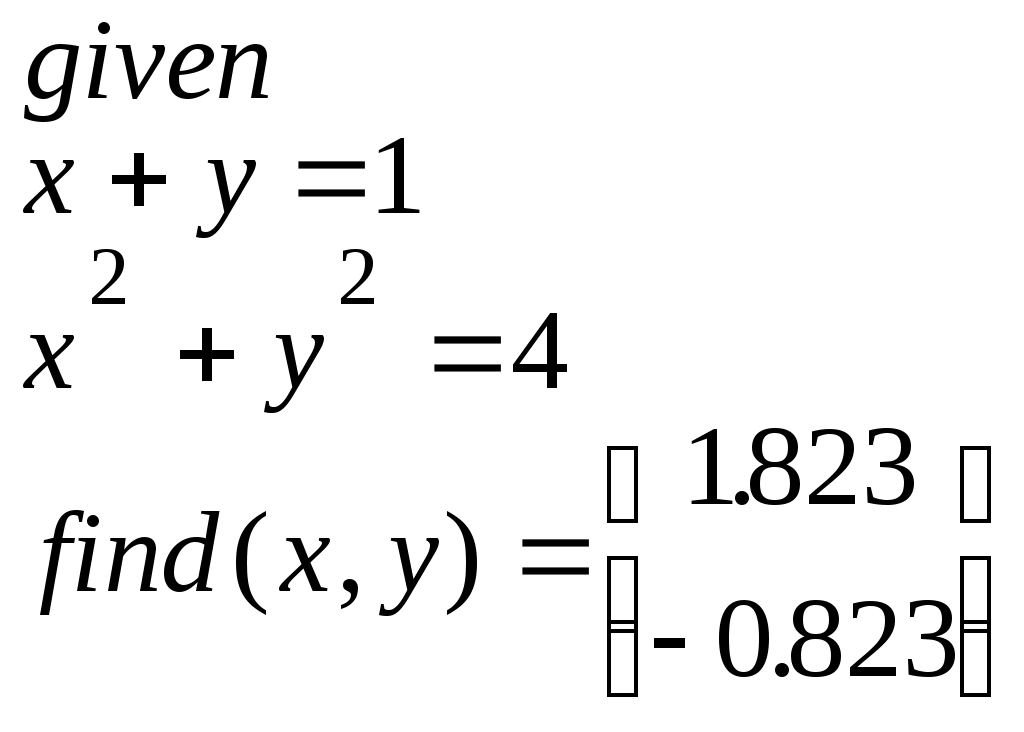
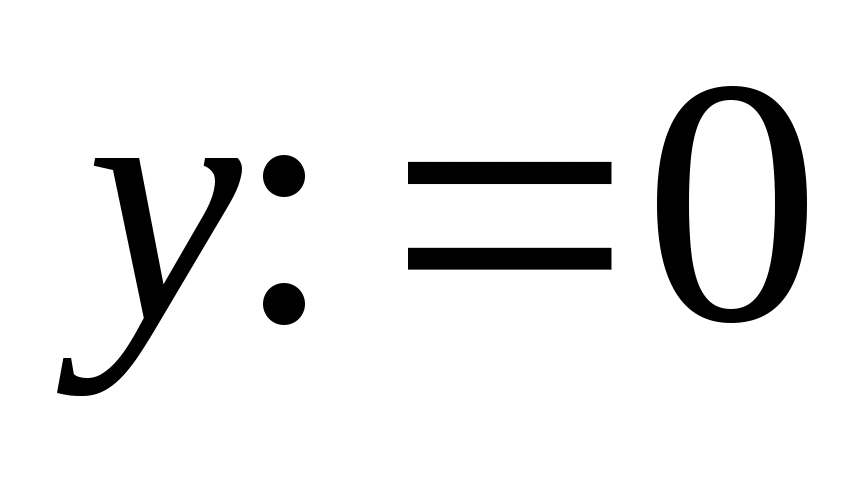
Для решения линейной системы уравнений Ax = b используется встроенная функция lsolve(A, b), где А – матрица системы, b – вектор правых частей. Функция возвращает вектор решений системы.
0>
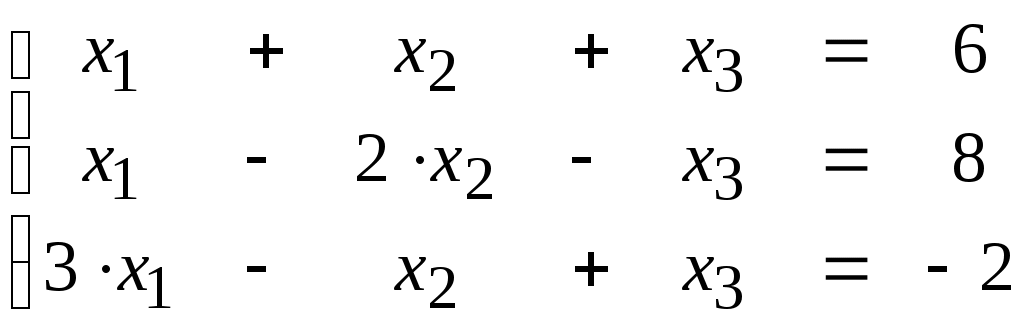
С помощью меню “Вставка” “Матрица” создадим шаблон матрицы из 3 строк и 3 колонок. Затем введем на место появившихся заполнителей
элементы матрицы А. Аналогично зададим вектор b, как матрицу из 3 строк и 1 колонки .
Для получения решения воспользуемся функцией lsolve. Для этого введем оператор
х := lsolve(A, b)
Для вывода ответа наберем х = .
Весь лист созданного документа должен выглядеть так:
Для решения задач поиска минимума или максимума какой-нибудь функции используются встроенные функции minimize и maximize, соответственно. Эти функции возвращают оптимальные значения переменных, от которых зависит целевая функция. Если требуется найти условный оптимум, то соответствующие условия нужно записать в блоке given.
Последовательность соответствующих операторов такова
1. Описание необходимых пользовательских функций, включая целевую и функций, используемых в ограничениях.
2. Указание начальных приближений к искомым переменным.
3. Запись системы ограничений в блоке given.
4. Вызов функции minimize или maximize.
Пример 1. Необходимо спроектировать ёмкость в виде тела вращения фиксированного объёма V0 = 25 и оптимальных размеров. Емкость изготавливается из листового железа, путём штамповки и сварки. В качестве критерия оптимальности используется длина сварного шва L.
Д
R
ополнительные условия: радиус основания R должен удовлетворять ограничениям R1 ≤ R ≤ R2, где R1 = 1, R2 = 3. Тело представляет прямой круговой цилиндр, размеры его Н – высота цилиндра и R – радиус основания.
K:=1..3
L:=1..3
:= + Восстановление матрицы с комплексными элементами по матрицам R и JМС=
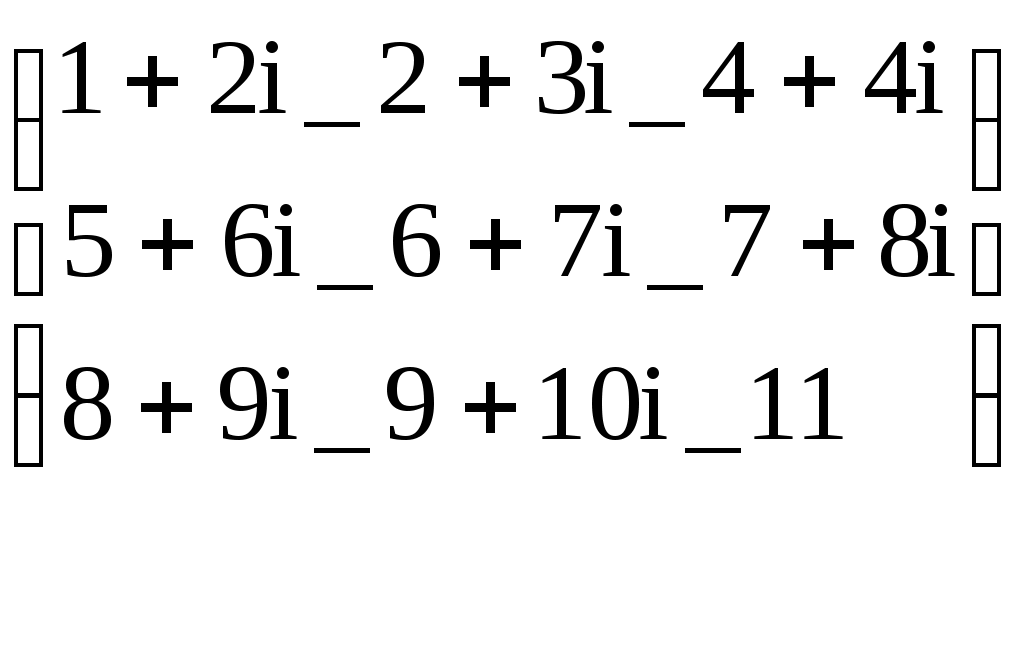Вывод восстановленной матрицы ( МС=СМ)3. Ранжированные переменные
До сих пор мы рассматривали переменные, которые имеют единственное значение. Однако в математике часто возникает необходимость в задании некоторого ряда значений – чаще всего упорядоченного. Например, для вычисления факториала N! = 12…(N-1)N нужно сформировать ряд чисел от 1 до N с шагом 1 и перемножить их. Также упорядоченный ряд значений какой-то переменной (например абсциссы x) нужен для построения графика функции – Mathcad строит графики функций по точкам, соединяя их по отрезкам прямых.
Для создания таких рядов в Mathcad используются так называемые ранжированные переменные. Иногда они заменяют управляющие структуры – циклы, однако полноценной такая замена всё же не является, в частности, потому что не предусмотрен выбор любого значения ранжированной переменной.
В самом простом случае для создания ранжированной переменной используется выражение: Name := Nbegin . . Nend, где Name – имя переменной, Nbegin – её начальное значение, Nend – конечное значение, .. – символ, указывающий на изменение переменной в заданных пределах (он вводится знаком точки с запятой ;). Если Nbegin < Nend, то шаг изменения переменной будет равен +1, в противном случае –1.
Для создания ранжированной переменной общего вида используется выражение: Name := Nbegin, (Nbegin + Step) . . Nend. Здесь Step – заданный шаг изменения переменной (он должен быть положительным, если Nbegin<Nend, или отрицательным в противном случае).
Примеры.
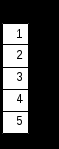
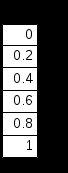
4. Построение графиков
Чтобы построить двумерный график в координатных осях X-Y, надо дать команду Insert – Graph – X-Y Plot (Вставка – График – Декартовые координаты). В области размещения графика находятся заполнители для указания отображаемых выражений и диапазона изменения величин. Заполнитель у середины оси координат предназначен для переменной или выражения, отображаемого по этой оси. Обычно используют ранжированную переменную или вектор значений. Граничные значения по осям выбираются автоматически в соответствии с диапазоном изменения величины, но их можно задать и вручную.
В одной графической области можно построить несколько графиков. Для этого надо у соответствующей оси перечислить несколько выражений через запятую.
Разные кривые изображаются разным цветом, а для форматирования графика надо дважды щелкнуть на области графика. Для управления отображением построенных линий служит вкладка Traces (Линии) в открывшемся диалоговом окне. Текущий формат каждой линии приведен в списке, а под списком расположены элементы управления, позволяющие изменять формат. Поле Legend Label (Описание) задает описание линии, которое отображается только при сбросе флажка Hide Legend (Скрыть описание). Список Symbol (символ) позволяет выбрать маркеры для отдельных точек, список Line (тип линии) задает тип линии, список Color (Цвет) – цвет. Список Type (Тип) определяет способ связи отдельных точек, а список Width (Толщина) – толщину линии.
Точно также можно построить и отформатировать график в полярных координатах. Для его построения надо дать команду Insert – Graph – Polar Plot (Вставка – График – Полярные координаты).
5. Решение уравнений и систем
Для численного поиска корней уравнения в программе MathCad используется функция root. Она служит для решения уравнений вида
, где
- выражение, корни которого нужно найти, а – неизвестное. Для поиска корней с помощью функции root, надо присвоить искомой переменной начальное значение, а затем вычислить корень при помощи вызова функции: . Здесь - функция переменной , используемой в качестве второго параметра. Функция root возвращает значение независимой переменной, обращающее функцию в 0. Например: Если уравнение имеет несколько корней (как в данном примере), то результат, выдаваемый функцией root, зависит от выбранного начального приближения.
Если надо решить систему уравнений (неравенств), используют так называемый блок решения, который начинается с ключевого слова given (дано) и заканчивается вызовом find (найти). Между ними располагают логические выражения, задающие ограничения на значения искомых величин, иными словами, уравнения и неравенства. Всем переменным, используемым для обозначения неизвестных величин, должны быть заранее присвоены начальные значения.
Чтобы записать уравнение, в котором утверждается, что левая и правая части равны, используется знак логического равенства – кнопка Boolean Equals (Логически равно) на панели инструментов Evaluation (Вычисление). Другие знаки логических условий также можно найти на этой панели.
Заканчивается блок решения вызовом функции find, у которой в качестве аргументов должны быть перечисленные искомые величины. Эта функция возвращает вектор, содержащий вычисленные значения неизвестных. Например:
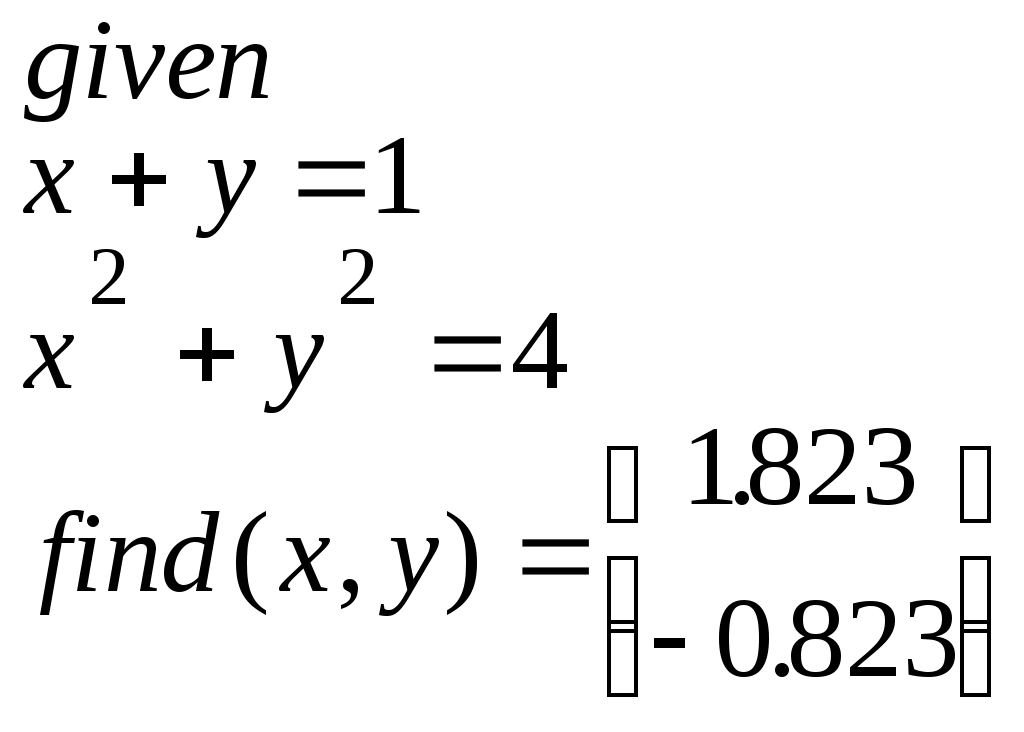
Для решения линейной системы уравнений Ax = b используется встроенная функция lsolve(A, b), где А – матрица системы, b – вектор правых частей. Функция возвращает вектор решений системы.
0>
Пусть необходимо решить систему
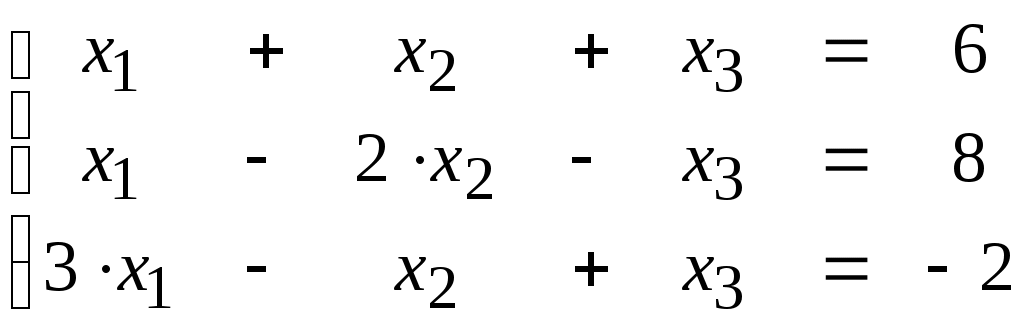
Создадим матрицу А системы и вектор b свободных членов (левых частей уравнений). Для этого наберем сочетание символов
А:
С помощью меню “Вставка” “Матрица” создадим шаблон матрицы из 3 строк и 3 колонок. Затем введем на место появившихся заполнителей
элементы матрицы А. Аналогично зададим вектор b, как матрицу из 3 строк и 1 колонки .
Для получения решения воспользуемся функцией lsolve. Для этого введем оператор
х := lsolve(A, b)
Для вывода ответа наберем х = .
Весь лист созданного документа должен выглядеть так:
6. Решение оптимизационных задач
Для решения задач поиска минимума или максимума какой-нибудь функции используются встроенные функции minimize и maximize, соответственно. Эти функции возвращают оптимальные значения переменных, от которых зависит целевая функция. Если требуется найти условный оптимум, то соответствующие условия нужно записать в блоке given.
Последовательность соответствующих операторов такова
1. Описание необходимых пользовательских функций, включая целевую и функций, используемых в ограничениях.
2. Указание начальных приближений к искомым переменным.
3. Запись системы ограничений в блоке given.
4. Вызов функции minimize или maximize.
Пример 1. Необходимо спроектировать ёмкость в виде тела вращения фиксированного объёма V0 = 25 и оптимальных размеров. Емкость изготавливается из листового железа, путём штамповки и сварки. В качестве критерия оптимальности используется длина сварного шва L.
Д
R
ополнительные условия: радиус основания R должен удовлетворять ограничениям R1 ≤ R ≤ R2, где R1 = 1, R2 = 3. Тело представляет прямой круговой цилиндр, размеры его Н – высота цилиндра и R – радиус основания.