Файл: Введение Вычислительная мощность компьютера позволяет использовать его как средство автоматизации научной работы.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 62
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
После щелчка по кнопке ОК в формулу вставляется матрица, содержащая вместо элементов заполнители. Вместо каждого заполнителя надо вставить число, переменную или выражение.
Для матриц определены следующие операции: сложение, умножение на число, перемножение и прочие. Допустимо использование матриц вместо скалярных выражений: в этом случае предполагается, что указанные действия должны быть применены к каждому элементу матрицы, и результат также представляется в виде матрицы. Например, выражение М+3, где М- матрица, означает, Что к каждому элементу матрицы прибавляется число 3. Если требуется указать необходимость поэлементного применения операции к матрице, используют знак векторизации, для ввода которого служит кнопка Vectorize (Векторизация) на панели инструментов Matrix (Матрица). Например
Для работы с элементами матрицы используют индексы элементов. Нумерация строк и столбцов матрицы начинается с нуля. Индекс элемента задается числом, переменной или выражением и отображается как нижний индекс. Он вводится после щелчка на кнопке Subscript (Индекс) на панели инструментов Matrix (Матрица).
Пара индексов, определяющих элемент матрицы, разделяется запятой. Иногда (например, при построении графиков) требуется выделить вектор, представляющий собой столбец матрицы. Номер столбца матрицы отображается как верхний индекс, заключенный в угловые скобки, например М<0>. Для своего ввода используется кнопка Matrix Column (Столбец) на панели инструментов Matrix (Матрица).
Векторные и матричные операторы
Для работы с векторами и матрицами система Mathcad содержит ряд операторов и функций. Вначале рассмотрим операторы, введя следующие обозначения для векторов V, для матриц M и для скалярных величин Z. Ниже представлены операторы для работы с векторами и матрицами.
Оператор Ввод Описание
| V1+V2 V1-V2 V-Z Z*V, V*Z Z*M, M*Z V1*V2 Оператор M*V M1*M2 | V1+V2 V1-V2 V-Z Z*V, V*Z Z*M, M*Z V1*V2 Ввод M*V M1*M2 V/Z M/Z M^-1 M^n V ctrl ! M ctrl ! V1 ctrl* V2 Alt $ V V ctrl – M ctrl – M ctrl^n V [ n M [ (m,n) | Сложение двух векторов V1 и V2 Вычитание двух векторов V1 и V2 Вычитание из всех элементов вектора V скаляра Z Умножение вектора V на скаляр Z Умножение матрицы M на скаляр Z Скалярное умножение двух векторов V1 и V2 Описание Умножение матрицы М на вектор V Умножение двух матриц М1 и М2 Деление всех элементов вектора V на скаляр Z Деление матрицы М на скаляр Z Обращение матрицы М Возведение матрицы М в степень n Вычисление модуля вектора V Вычисление определителя матрицы М Транспонирование вектора V Транспонирование матрицы М Векторное умножение двух векторов V1 и V2 Вычисление суммы элементов вектора V Векторизация вектора V Векторизация матрицы М Выделение n-го столбца матрицы М Выделение n-го элемента вектора V Выделение элемента (m,n) матрицы М |
Следует отметить, что в некоторых операторах для ввода используется клавиша Ctrl, тогда как в более ранних версиях Mathcad использовалась клавиша Alt( в последней версии клавиша Alt используется для активизации строки меню). Все представленные выше операторы (кроме последнего) могут вызываться из палитры матричных операций.
Работа с векторными и матричными функциями
Существует также ряд встроенных векторных и матричных функций. Они облегчают решение задач линейной алгебры и других сфер приложения векторов и матриц. Приведём список векторных функций, входящих в систему Mathcad:
• length(V) – возвращает число элементов вектора.
• last(V)- возвращает номер последнего элемента
• max(V)- возвращает максимальный элемент по значению элемент вектора( или матрицы)
• min(V)- возвращает минимальный по значению элемент вектора( или матрицы)
• re(V)- возвращает вектор действительных частей вектора с комплексными элементами
• Im(V)- возвращает вектор мнимых частей вектора с комплексными элементами
Для работы с матрицами также существует ряд встроенных функций. Они перечислены ниже:
• augment(M1, M2)- объединяет в одну две матрицы М1 и М2, имеющие одинаковое число строк ( объединение идет бок о бок)
• identity(n)- создает единичную квадратную матрицу размером
• stack(M1, M2)- объединяет две матрицы М1 и М2, имеющие одинаковое число столбцов, «сажая» М1 над М2
• submatrix(A, ir, jr, ic, jc)- возвращает подматрицу, состоящую из всех элементов, содержащихся в строках от ir до jr и столбцов c ic по jc ( ir ≤ jr и ic ≤ jc)
• diag(V)- создает диагональную матрицу, элементы главной диагонали которой равны элементам вектора
• matrix(m, n, f)- создает матрицу , в которой ( I , j)-й элемент равен а( I, j), где I=0, 1,…m и j=0,1,…n; f(I, j) некоторая функция.
• Re(M)- возвращает матрицу действительных частей матрицы М с комплексными элементами.
• Im(M)- возвращает матрицу мнимых частей матрицы М с комплексными элементами.
Функции, возвращающие специальные характеристики матриц
Следующие функции возвращают специальные характеристики матриц:
• cols(M) - возвращает число столбцов матрицы М;
• rows(M) - возвращает число строк матрицы М;
• rank(M) - возвращает ранг матрицы М;
• tr(M) - возвращает след (сумму диагональных элементов) квадратной матрицы М;
• mean(M)- возвращает среднее значение элементов массива М;
• median(M)- возвращает медиану элементов массива М;
• cond1(M)- возвращает число обусловленности матрицы, вычисленное в норме L1;
• cond2(M)- возвращает число обусловленности матрицы, вычисленное в норме L2;
• conde(M)- возвращает число обусловленности матрицы, вычисленное в норме евклидового пространства;
• condi((M)- возвращает число обусловленности матрицы, основанное на равномерной норме;
• norm1(M)- возвращает норму L1 матрицы М;
• norm2(M)- возвращает норму L2 матрицы М;
• norme(M)- возвращает Евклидову норму матрицы М;
• normi(M)- возвращает неопределённую норму матрицы М.
Примеры применения векторных и матричных операторов.
V:=
V1:=
V3:=V1·V2 V3=26 Умножение двух векторов
V4:= V1
V:=
U:=
U
 := ln(V) U=
:= ln(V) U=U1= 0.693 Выделение элемента вектора U
Lenath(V) = 3 Вычисление встроенных функций вектора V
Max(V)= 3
Mathcad делает работу с векторами и матрицами столь же простой, как и с обычными числами и переменными. Это, безусловно, способствует проникновению векторных и матричных методов математических вычислений в практику научно-технических и иных расчетов. Р
ДЕЙСТВИЯ С МАТРИЦАМИ –1
A:=
B:=
M:=identity(2) M=
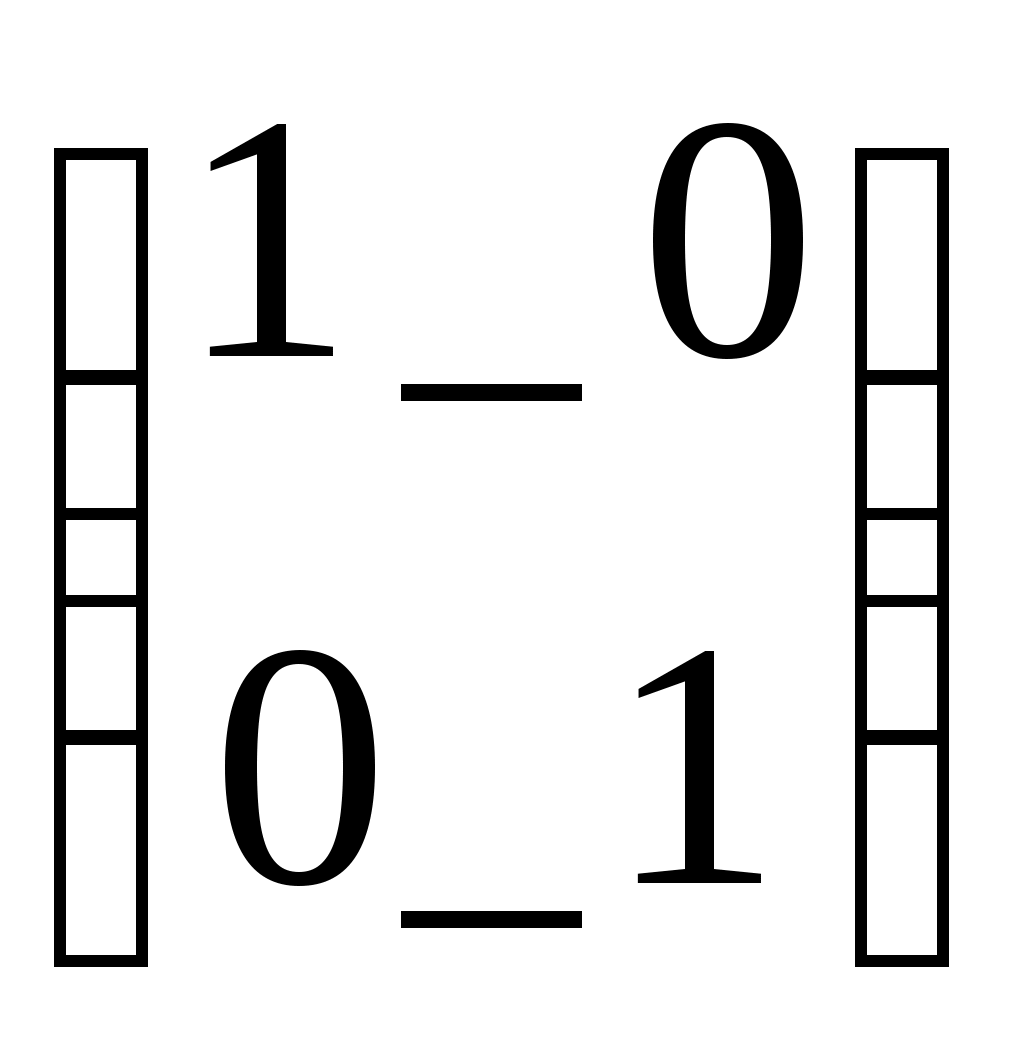 Создание единичной матрицы М
Создание единичной матрицы МTr(M)=2 Вычисление следа матрицы
A:=
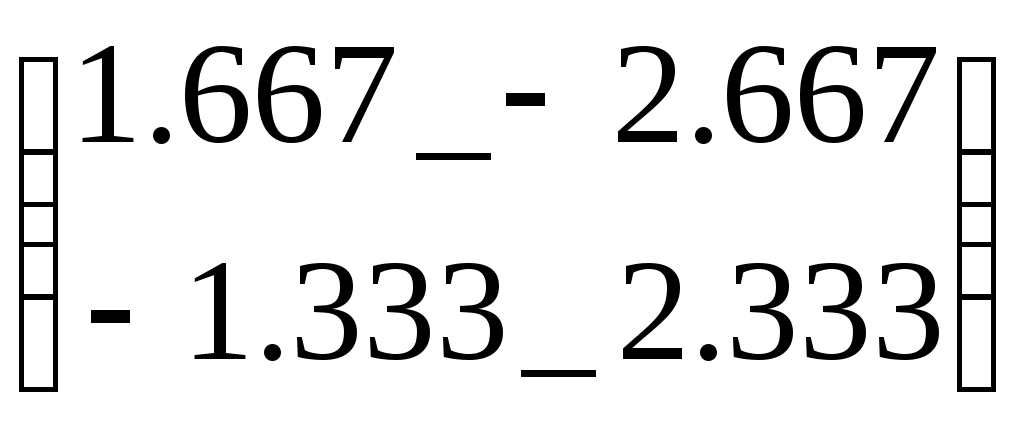 Задание и обращение матрицы А
Задание и обращение матрицы АC:=
A:=
A:=
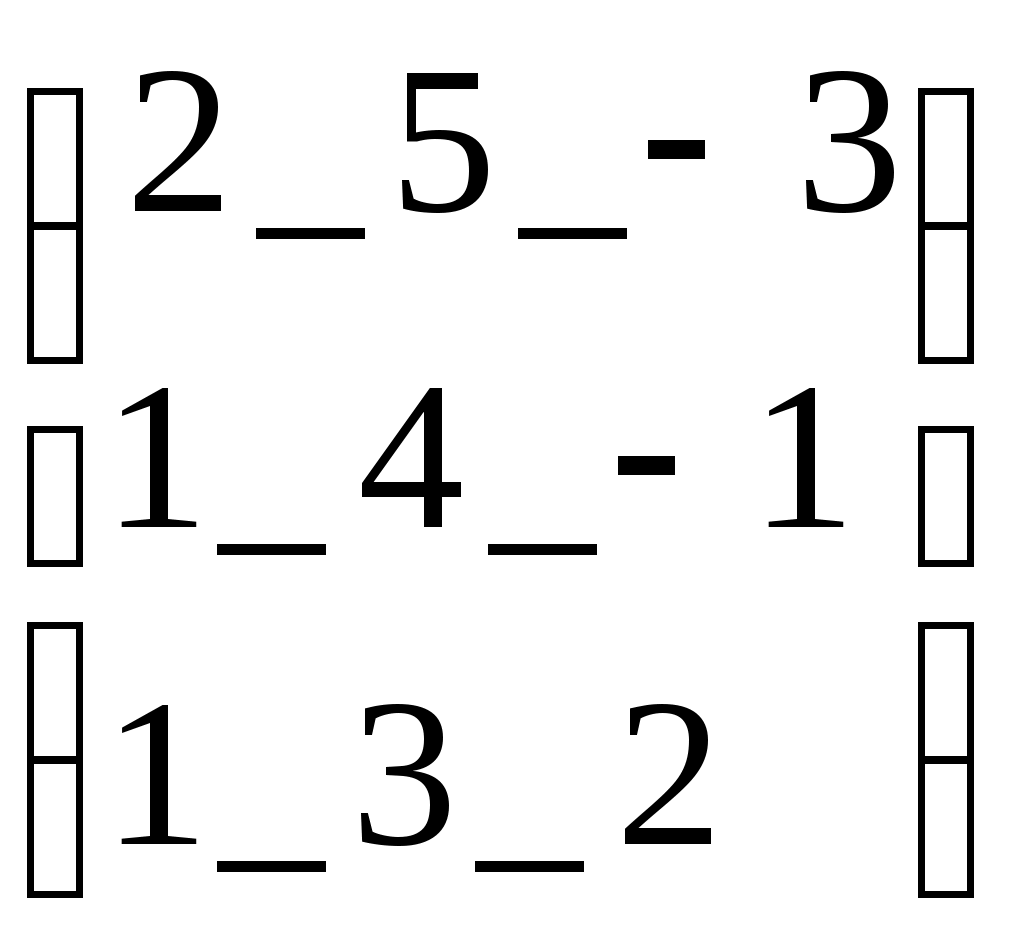 D:=
D:=ДЕЙСТВИЯ С МАТРИЦАМИ –2
=4
А:=
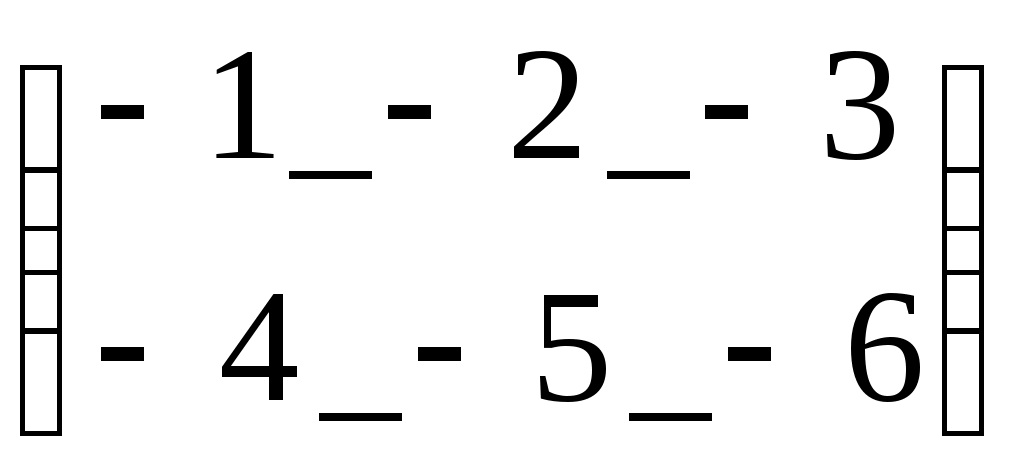
2·А=
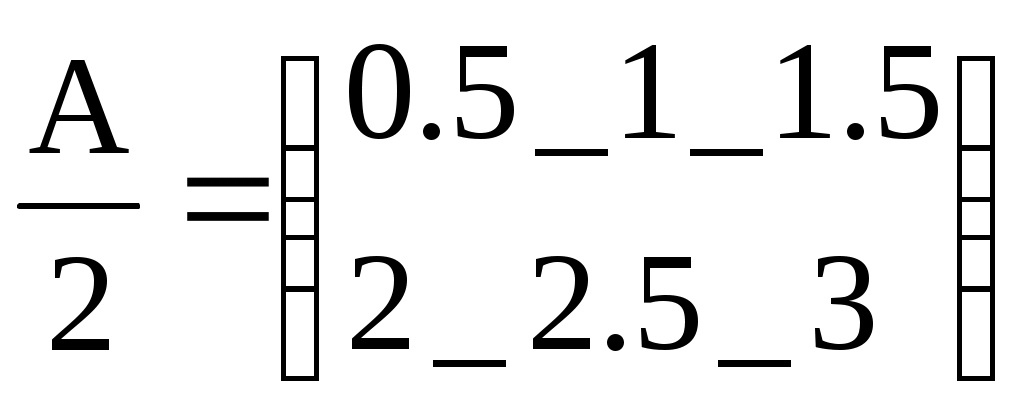 Задание матрицы А, смена знака у всех её
Задание матрицы А, смена знака у всех её элементов, удвоение их и деление на два
А:=
W
 :=exp(V) W=
:=exp(V) W= Векторизация вектора W
Векторизация вектора W I:=
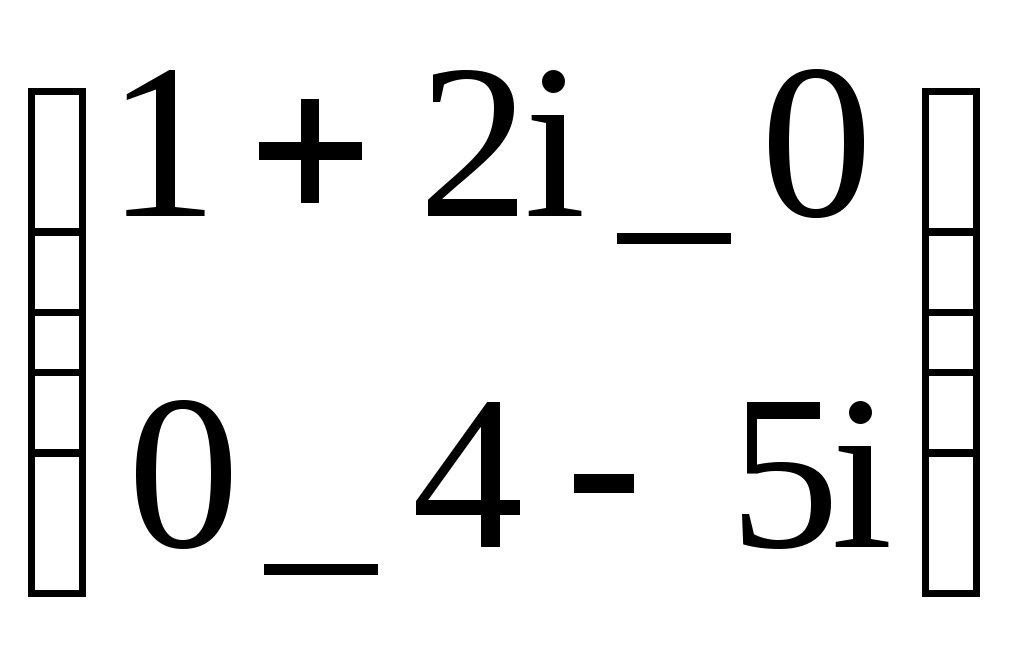 Задание матрицы А с комплексными элементами
Задание матрицы А с комплексными элементамиM1:= identity(3) M1=
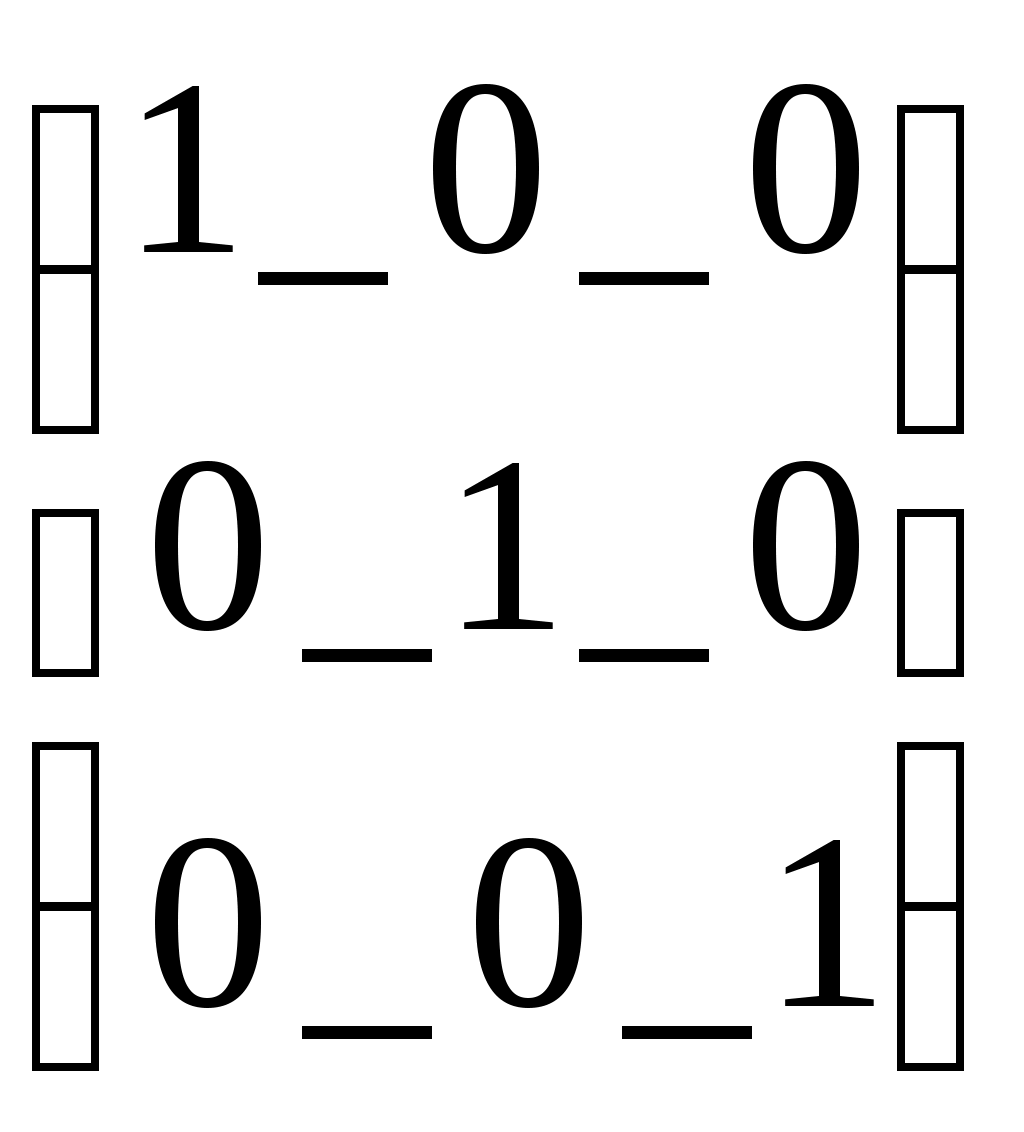 Задание и вывод единичной квадратной матрицы М1
Задание и вывод единичной квадратной матрицы М1 V:=
М2:=
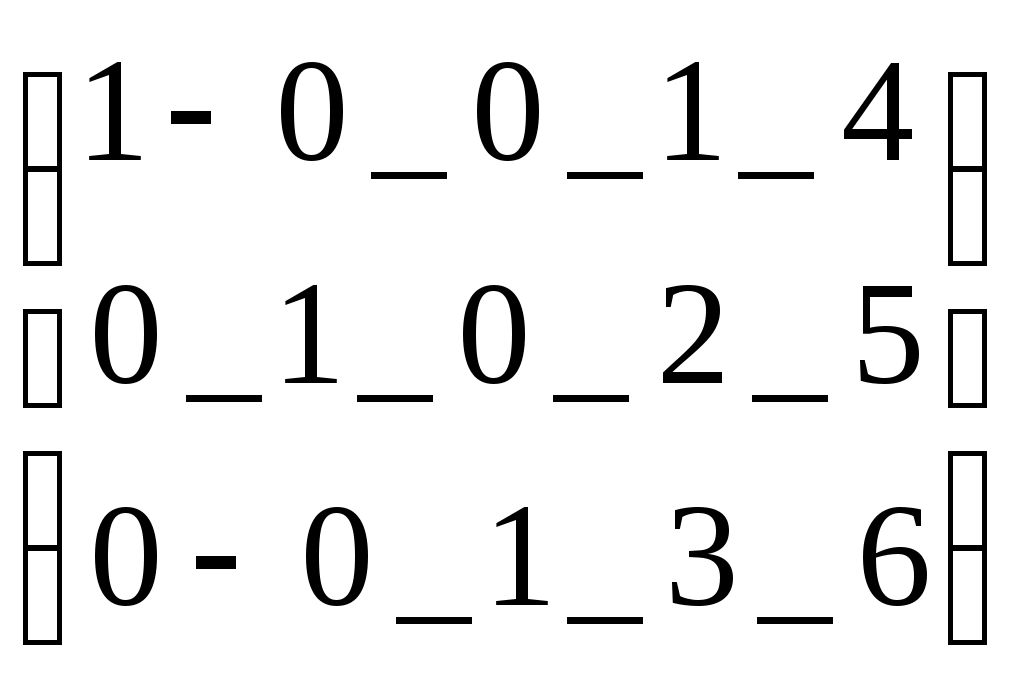 Задание матрицы М2 и подключение ее к матрице М1
Задание матрицы М2 и подключение ее к матрице М1Tr(M1)=3 Вычисление следа матрицы М1: суммы диагональных эдементов
i:=
Задание матрицы СМ с комплексными элементами
CM:=
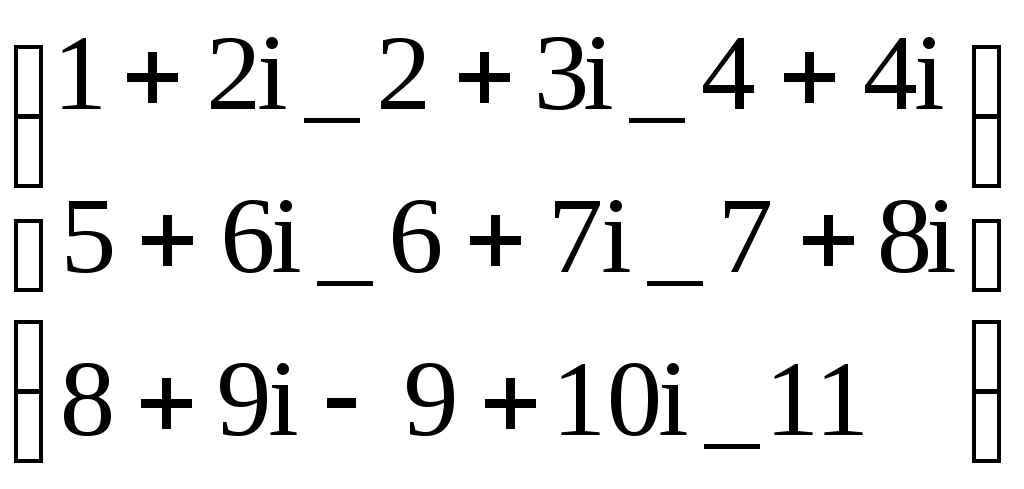
R:=Re(CM) R=
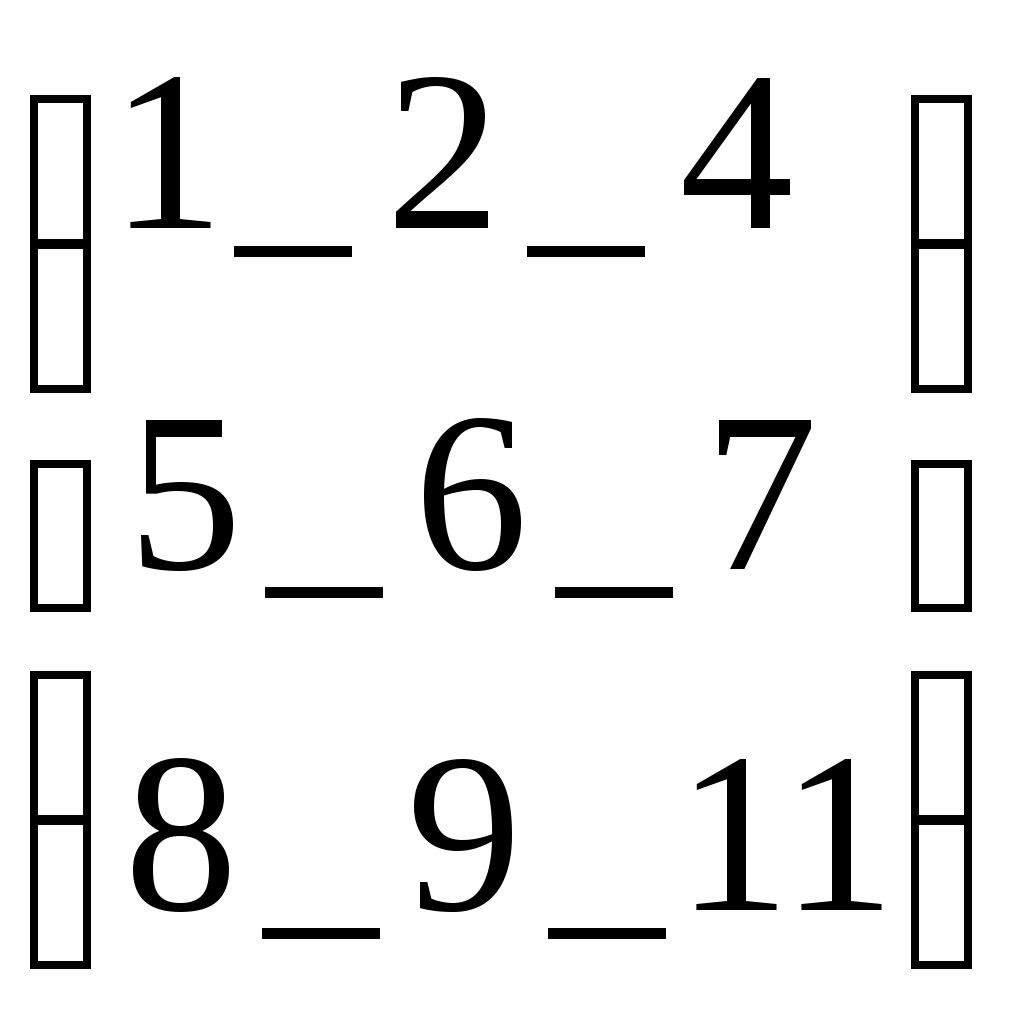 Выделение матрицы- действительной части матрицы СМ
Выделение матрицы- действительной части матрицы СМ J:=lm(CM) J=
