Файл: Введение Вычислительная мощность компьютера позволяет использовать его как средство автоматизации научной работы.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 61
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.


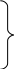
Н
Расчетные формулы:
V = πR2 Н
L = 4 πR + Н
Лист созданного документа должен выглядеть так:
Пример 2. Решить задачу линейного программирования:
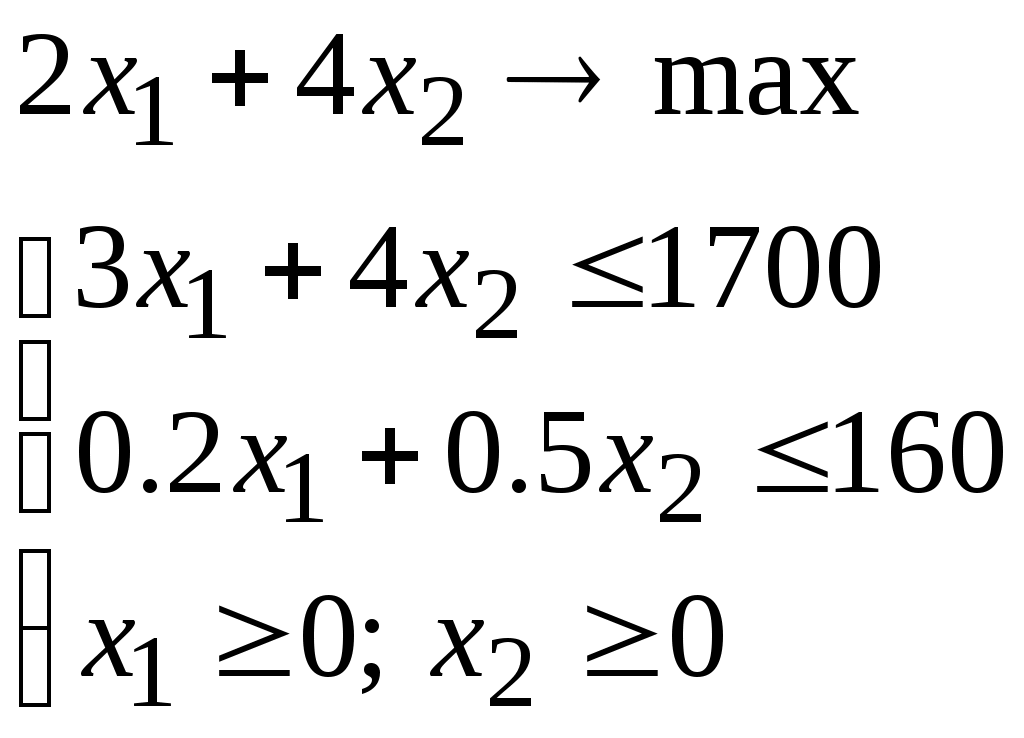
Документ решения:


7. Статистические функции
В MathCad имеется набор статистических функций, относящихся к наиболее распространенным законам распределения. Характер функции для каждого закона распределения определяется первой буквой ее имени:
-
d (density) – плотность распределения вероятностей f(x) -
p (probability) – функция распределения вероятностей F(x) -
q (quintile) – обратная функция распределения случайной величины – квантиль – такое значение аргумента х, при котором вероятность случайного события < х равна заданной величине р. -
r (random) – вектор случайных чисел.
Вид соответствующего закона распределения определяется второй частью имени статистической функции:
-
norm(y, m, ) – нормальный закон; y – аргумент функции, m – математическое ожидание, – стандартное отклонение. -
unif(y, a, b) – равномерный закон; y – аргумент функции, a, b – границы интервала распределения. -
exp(y, ) – показательный (экспоненциальный) закон; y – аргумент функции, – параметр распределения. -
chisq(y, n) – распределение Пирсона; y – аргумент функции, n – число степеней свободы – параметр распределения. -
F(y, n1, n2) – распределение Фишера; y – аргумент функции, n1, n2 – числа степеней свободы числителя и знаменателя – параметры распределения. -
t(y, n) – распределение Стьюдента; y – аргумент функции, n – число степеней свободы – параметр распределения.
Замечание. Аргументом функций типа d, p является значение х,
- аргументом функции типа q является значение вероятности p,
- аргументом функции типа r является N – размерность сгенерированного случайного вектора.
Например.
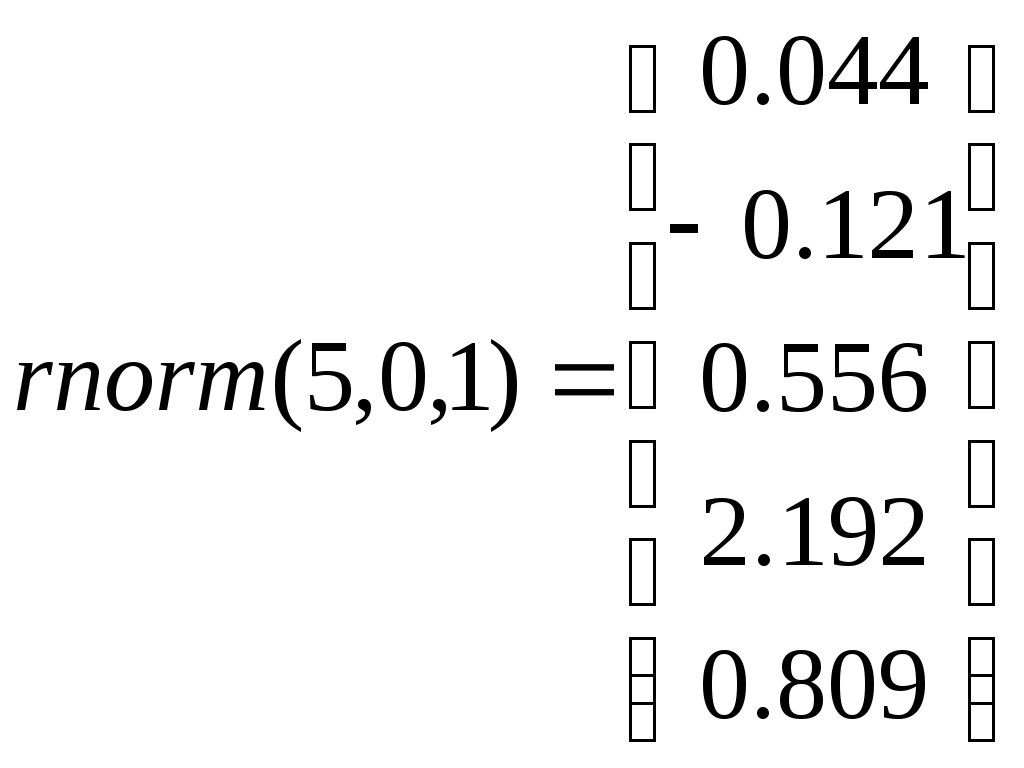
Другие статистические функции
-
mean(A) – среднее арифметическое массива А – оценка математического ожидания; -
Var(A) – несмещенная оценка дисперсии для элементов массива А: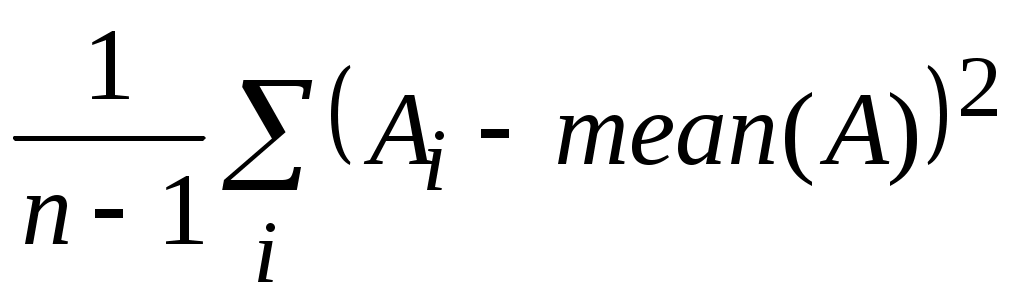 :
: -
var(A) – смещенная оценка дисперсии для элементов массива А: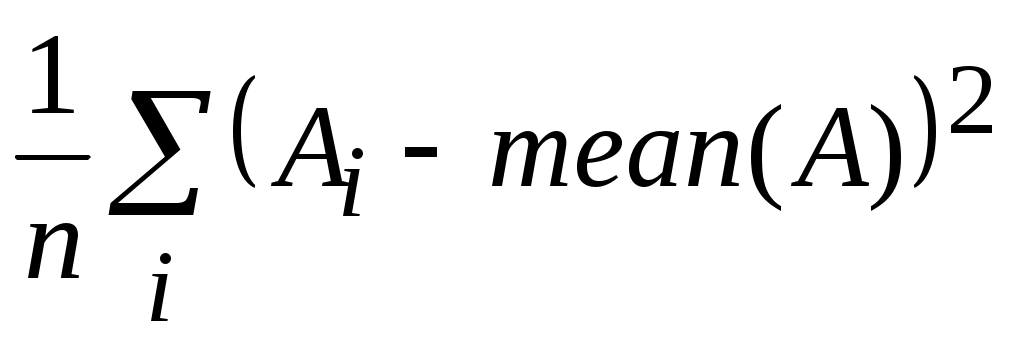 :
:
Например,

8. Аналитические вычисления
С помощью аналитических вычислений находят аналитические или полные решения уравнений и систем, а также проводят преобразования сложных выражений (например, упрощение). Иначе говоря, при таком подходе можно получить нечисловой результат. В программе MathCad конкретные значения, присвоенные переменным, при этом игнорируются – переменные рассматриваются как неопределенные параметры. Команды для выполнения аналитических вычислений в основном сосредоточены в меню Symbolics (Аналитические вычисления).
Чтобы упростить выражение (или часть выражения), надо выбрать его при помощи уголкового курсора и дать команду Symbolics – Simplify (Аналитические вычисления – Упростить). При этом выполняются арифметические действия, сокращаются общие множители и приводятся подобные члены, применяются тригонометрические тождества, упрощаются выражения с радикалами, а также выражения, содержащие прямую и обратную функции (типа
Команду Symbolics – Simplify (Аналитические вычисления - Упростить) применяют и в более сложных случаях. Например, с ее помощью можно:
-
вычислить предел числовой последовательности, заданной общим членом; -
найти общую формулу для суммы членов числовой последовательности, заданной общим членов; -
вычислить производную данной функции; -
найти первообразную данной функции или значение определенного интеграла.
Другие возможности меню Symbolics (Аналитические вычисления) состоят в выполнении аналитических операций, ориентированных на переменную, использованную в выражении. Для этого надо выделить в выражении переменную и выбрать команду из меню Symbolics – Variable (Аналитические вычисления - Переменная). Команда Solve (Решить) ищет корни функции, заданной данным выражением, например, если выделить уголковым курсором переменную x в выражении
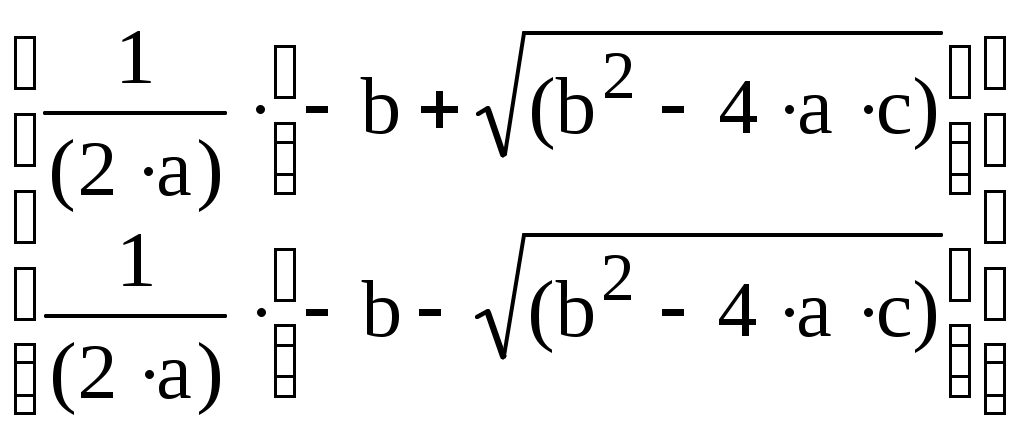 .
.Другие возможности использования этого меню:
-
аналитическое дифференцирование и интегрирование: Symbolics – Variable – Differentiate (Аналитические вычисления – Переменная - Дифференцировать) и Symbolics – Variable – Integrate (Аналитические вычисления – Переменная – Интегрировать); -
замена переменной Symbolics – Variable – Substitute (Аналитические вычисления – Переменная – Подставить) – вместо переменной подставляется содержимое буфера обмена; -
разложение в ряд Тейлора: Symbolics – Variable – Expand to Series (Аналитические вычисления – Переменная – Разложить в ряд); -
Представление дробно- рациональной функции в виде суммы простых дробей с линейными и квадратичными знаменателями: Symbolics – Variable – Convert to Partial Fraction (Аналитические вычисления – Переменная – Преобразовать в простые дроби).
Наконец, самым мощным инструментом аналитических вычислений является оператор аналитического вычисления, который вводится с помощью кнопки Symbolics Evaluation (Вычислить аналитически) на панели инструментов Evaluation (Вычисление). Его можно, например, использовать для аналитического решения системы уравнений и неравенств. Блок решения задается точно так же, как при численном решении (хотя начальные значения переменных можно не задавать), а последняя формула блока должна выглядеть как
Любое аналитическое вычисление можно применить с помощью ключевого слова. Для этого используют кнопку Symbolics Keyword Evaluation (Вычисление с ключевым словом) на панели инструментов Evaluation (Вычисление). Ключевые слова вводятся через панель инструментов Symbolics (Аналитические вычисления). Они полностью охватывают возможности, заключенные в меню Symbolics (Аналитические вычисления), позволяя также задавать дополнительные параметры.
9. Файловые данные
Mathcad может успешно использоваться в современных физических установках для обсчета данных эксперимента. Но для этого необходима связь между такими установками (точнее, их программным обеспечением) и системой Mathcad. Для реализации подобной связи система Mathcad имеет специальный тип данных – файловые данные. В сущности, это те же векторы и матрицы, но с элементами, которые могут записываться в виде файлов текстового формата, имеющих свои имена. Файлы данных в системе представляют собой запись матриц в их естественной форме.
Имеются операции считывания таких файлов, позволяющие присваивать содержащиеся в них данные переменным, векторам или матрицам.
В ходе создания файла система считывает значения элементов вектора или матрицы поэлементно ( для матриц слева направо и сверху вниз) и по ходу считывания преобразует числовые значения элементов в их символьные эквиваленты, использующие ASCII- коды цифр и относящихся к заданию чисел символы. Эти символьные значения и записываются в виде файлов данных.
Существуют простые функции для работы с файловыми данными, используемые во всех версиях Mathcad для Windows. Создаваемые или обрабатываемые ими файлы легко просмотреть в любом текстовом редакторе, воспринимающим тексты в виде ASCII- кодов. При считывании файлов система обеспечивает обратное преобразование символьных представлений значений элементов в их числовые значения. Такая форма задания облегчает стыковку Mathcad с программами, написанными на любом языке программирования, даже таком простом, как Бейсик или Паскаль, и обеспечивает взаимный обмен файлами текстового формата.
Функция READPRN(“Имя_файла.prn”) считывает данные из файла с именем Имя_файла. Аргументом функции является строковая переменная, по этой причине собственно Имя_файла помещается в обращении к функции в кавычки.
Функция READPRN возвращает матрицу, значения элементов которой однозначно связаны со значениями элементов файла. Или, точнее, каждая строка или столбец возвращаемой матрицы подобны соответствующим строкам или столбцам текстового представления файла. например:
M := READPRN(“DATA.prn”)
Элементы матрицы М получают значения, считанные из файла с именем DATA,prn. Естественно, что такой файл должен существовать на диске, иначе ситуация будет считаться ошибочной. Для указания полного имени файла (если он не находится в текущей папке системы) следует использовать общеупотребительные для MS-DOS составные имена, например D:\EXPER\DATA.prn, если файл DATA расположен на диске D в папке EXPER.
Функция WRITEPRN(“Имя_файла.prn”) записывает матрицу в файл и присваивает ему указанное имя. Структура файла подобна структуре матрицы. Данные могут порождаться математическим выражением, например:
WRITEPRN(“Имя_файла.prn”) := Выражение