ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 111
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Решение:
Индекс стоимости продукции (товарооборота) представляет собой соотношение стоимости продукции текущего периода к стоимости продукции в базисном периоде и определяется по формуле:
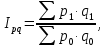
где pi – цена в текущем периоде, p0 – цена в базовом периоде, qi –количество товара, реализованного в отчетный период, q0 – количество товара, реализованного в базисном периоде.
Ipq = 3146/ 4138,8= 0,7601 или 76,01%.
Стоимость продукции отчетного периода по сравнению с базисным периодом, снизилась на 23,99%.
Сводный индекс физического объема продукции - характеризует изменение количества проданных товаров не в денежных, а в физических единицах измерения (взвешенный по себестоимости), определяется по формуле:
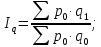
Iq = 4051,2/ 4138,8 = 0,9788 или 97,88%.
Количество проданных товаров отчетного периода по сравнению с базисным периодом, снизилось на 2,11%.
Сводный индекс – это относительный показатель, который характеризует среднее изменение социально–экономического явления состоящего из несоизмеримых показателей, который рассчитывается по формуле:
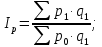
Ip = 3146/ 4051,2 = 0,7765 или 77,65%.
Цены отчетного периода по сравнению с базисным периодом, снизились на 22,35%.
Ответ:
Сводный индекс стоимостного объема продукции = 0,7601. Товарооборот в отчетном периоде снизился на 23,99%.
Сводный индекс физического объема продукции = 0,9788. Физический объем в отчетном периоде снизился на 2,11%.
Сводный индекс цен = 0,7765.Цены в отчетном периоде снизились на 22,35%.
Тема: Графическое изображение статистических данных
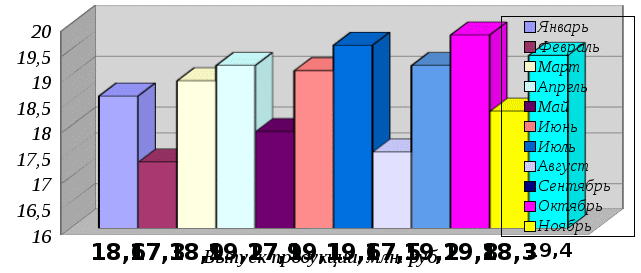
Задание 1. По данным таблицы построить графики динамики в виде линейной и столбиковой диаграмм.
| Месяцы | Выпуск продукции, млн. руб. | Месяцы | Выпуск продукции, млн.руб. |
| Январь | 18,6 | Июль | 19,6 |
| Февраль | 17,3 | Август | 17,5 |
| Март | 18,9 | Сентябрь | 19,2 |
| Апрель | 19,2 | Октябрь | 19,8 |
| Май | 17,9 | Ноябрь | 18,3 |
| Июнь | 19,1 | Декабрь | 19,4 |
-
Линейная диаграмма
-
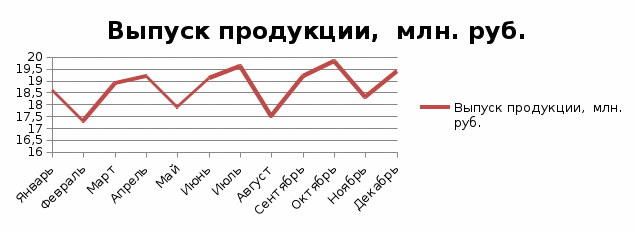
Столбиковая диаграмма
Тема: Взаимосвязи экономических явлений
Задание 1. По данным таблицы построить аналитическое уравнение зависимости разряда рабочих от стажа работы. С помощью линейного коэффициента корреляции определить тесноту связи между явлениями.
Таблица 1
| № n/n рабочих | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Разряд (у) | 3 | 2 | 4 | 5 | 5 | 5 | 5 | 5 | 6 | 5 | 1 | 4 |
| Стаж работы, лет (х) | 7 | 7 | 25 | 23 | 18 | 24 | 11 | 16 | 34 | 11 | 1 | 20 |
Определим форму зависимости разряда рабочих от стажа их работы на предприятии, используя графический метод:
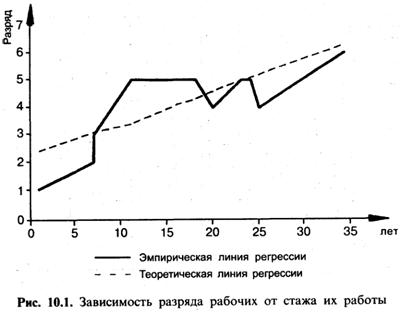
Рисунок 1 - Зависимость разряда рабочих от стажа работы
Судя по распределению, зависимость прямолинейная.
Как известно, прямолинейная зависимость подчиняется уравнению прямой:
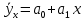
Следовательно, параметры данного уравнения связи находятся путем решения следующей системы уравнений:
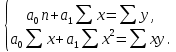
Для решения системы построим вспомогательную таблицу 2.
Таблица 2
| Стаж*; лет (x) | Разряд (у) | ху | x2 | y2 | ух |
| 1 | 1 | 1 | 1 | 1 | 2,4 |
| 7 | 2 | 14 | 49 | 4 | 3,1 |
| 7 | 3 | 21 | 49 | 9 | 3,1 |
| 11 | 5 | 55 | 121 | 25 | 3,4 |
| 16 | 5 | 80 | 256 | 25 | 4,1 |
| 18 | 5 | 90 | 324 | 25 | 4,3 |
| 20 | 4 | 80 | 400 | 16 | 4,6 |
| 23 | 5 | 115 | 529 | 25 | 5 |
| 24 | 5 | 120 | 576 | 25 | 5,1 |
| 25 | 4 | 100 | 625 | 16 | 5,2 |
| 34 | 6 | 204 | 1156 | 36 | 6,3 |
| Итого: 197 | 50 | 935 | 4207 | 232 | 50 |
На основе данных таблицы 2 имеем систему уравнений в следующем виде:
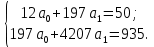
Решим систему сравнений:
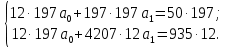
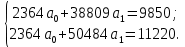
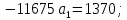
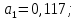
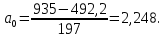
Следовательно, найденное аналитическое уравнение связи имеет вид:
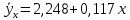
Подставим соответствующие значения х в уравнение и найдем новые значения
.
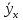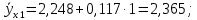
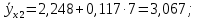
Изобразим по найденным значениям
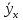теоретическую линию регрессии, которая, как видно, с некоторыми погрешностями воспроизводит эмпирическую линию регрессии (см. рис. 1).Так как
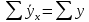, то можно считать, что построенное парное уравнение корреляции является искомым, и мы вправе сделать следующий вывод: с увеличением стажа работы на один год разряд рабочих в среднем возрастает на 0,117.Экономическая интерпретация аналитического уравнения связи может осуществляться с помощью коэффициента эластичности. Расчетная величина коэффициента эластичности:
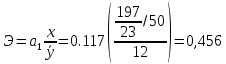
Таким образом, увеличение стажа работы на 1 процент приводит к увеличению разряда на 0,456 процента.
Для установления тесноты связи между факторным и результативным признаками в случае линейной зависимости применяется линейный коэффициент корреляции.
Рассчитаем величину линейного коэффициента корреляции:
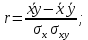
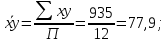
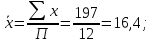
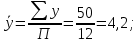
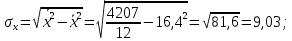
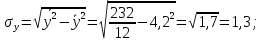
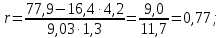
Как видно, связь между разрядом рабочего и стажем его работы на предприятии достаточно значительная, так как r = 0,77 близко к «1».
Для установления размера вариации разряда рабочего от стажа его работы рассчитываем коэффициент детерминации:
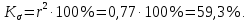
Следовательно, на 59,3% вариация разряда рабочего объясняется изменением стажа его работы на предприятии.
Проведем анализ взаимосвязи между явлениями по сгруппированным данным, представленным в виде корреляционной таблицы, характеризующей связь между стажем рабочих и их заработной платой (табл. 3).
Таблица 3
| Стаж работы, лет (х) | Заработная плата, тыс. руб. | Итого | | |||||||
| 40—50 | 50—60 | 60—70 | 70—80 | 80—90 | 90—100 | 100—110 | | |||
| 0—5 | 5 | 7 | 14 | 8 | 1 | | 35 | | ||
| 5—10 | | 3 | 4 | 10 | 5 | 2 | 125 | | ||
| 10—15 | | | 2 | 4 | 9 | | 217 | | ||
| 15—20 | | | | 3 | 2 | 5 | 111 | | ||
| 20—25 | | | | | 3 | 3 | 17 | | ||
| 25—30 | | | | | | 5 | 5 | | ||
| Итого ny: | 5 | 10 | 20 | 25 | 20 | 15 | 5100 | | ||