ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 122
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ВЕРОЯТНОСТИ СОБЫТИЙ
Испытанием называется опыт, эксперимент, наблюдение явления в определенных условиях. Испытание может привести к одному из нескольких результатов.
Событие – результат (исход) испытания. Например, бросание игральной кости – испытание, а выпадение определенного числа очков – событие.
События можно подразделить на три вида: случайные, достоверные и невозможные.
Случайным называется событие, которое может произойти, а может и не произойти при испытании. Случайные события обозначаются заглавными буквами латинского алфавита: A, B, X, Y.
Достоверным называется событие, которое обязательно происходит в каждом испытании. Достоверные события обозначаются символом U.
Невозможным называется событие, которое не происходит ни при одном испытании. Невозможные события обозначаются символом .
Вероятностью события А называется отношение числа m случаев, благоприятствующих его наступлению, к числу n всех возможных случаев. Обозначение:
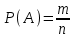. Вероятность - это числовая характеристика возможности наступления какого-либо события.
Свойства вероятности
1) Вероятность любого события заключена между нулем и единицей, т.е.
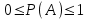. 2) Вероятность достоверного события равна единице, т.е.
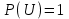
3) Вероятность невозможного события равна нулю, т.е.
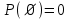
Операции над событиями
Суммой двух событий A, B называется событие, состоящее в появлении хотя бы одного из данных событий.
Обозначается: А + В. Читается А или В
Сумма А + В означает, что наступят событие А, или В, или оба вместе.
    А + В В А |    АВ В А |
Произведением двух событий А, В называется событие, состоящее в одновременном появлении данных событий.
Обозначается: АВ. Читается А и В.
Произведение АВ означает, что наступают одновременно два события.
Два события называются независимыми, если вероятность появления каждого из них не зависит от того, появилось другое событие или нет. В противном случае события называются зависимыми.
Два события называются совместными, если появление одного из них не исключает появление другого в одном и том же испытании. В противном случае события называются несовместными, т.е. появление одного из них исключает появление другого в одном и том же испытании.
Несколько попарно несовместных событий образуют полную группу, если в результате испытания одно из них обязательно. Например, множество выпадений числа очков при однократном бросании игральной кости
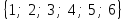образует полную группу событий.Два несовместных события называются противоположными, если в результате испытания одно из них обязательно произойдет. Событие, противоположное событию А, принято обозначать
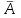.Теорема. Сумма вероятностей событий А1 , А2 , ..., Аn , образующих полную группу, равна единице:
Р (A1) + Р (А2) + ... + Р (Аn) = 1.
Следствие. Сумма вероятностей противоположных событий равна единице:
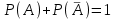, или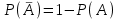 
, т.е. вероятность противоположного события равна единице минус вероятность самого события.Теорема. Вероятность произведения двух независимых событий A и B равна произведению этих вероятностей: P (AB) = P (A) P (B).
Теорема. Вероятность суммы двух несовместных событий A и B равна сумме вероятностей этих событий: P(A + B) = P(A) + P(B).
Теорема. Вероятность суммы двух совместных событий A и B равна сумме вероятностей этих событий минус вероятность их произведения:
P(А + B) = P(А) + P(B) – Р(АВ).
Замечание. Сумма двух совместных событий есть появление хотя бы одного из этих событий. События
А + B и
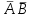- противоположные, поэтомуP(А + B) = 1 - P(
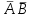).Условная вероятность. Пусть А и В - зависимые события. Условной вероятностью PA (B) события В называется вероятность события В, найденная в предположении, что событие А уже наступило.
Теорема. Вероятность произведения двух зависимых событий A и B равна произведению вероятности одного из них на условную вероятность другого, найденного в предположении, что первое событие уже наступило:
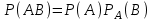
Задачи на классическое определение вероятности
Пример 1. В сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос по неравенствам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам.
▼ Событие А – выбор билета без вопроса по неравенствам. Всего n = 25 билетов. Благоприятствующих событию А исходов m = 25 – 10 = 15. Тогда
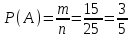= 0,6.Ответ: 0,6.▲
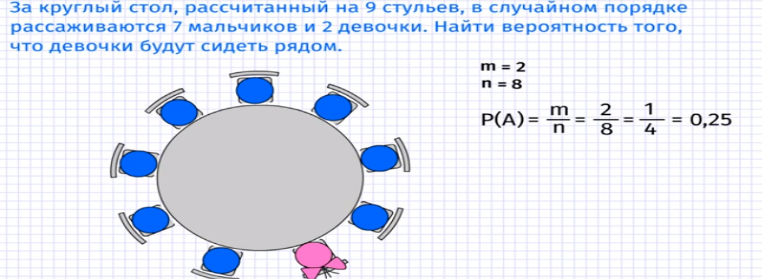
Задание. За круглый стол на 9 стульев в случайном порядке рассаживаются 7 мальчиков и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть рядом.
▼ Пусть первой за стол сядет девочка, рядом с ней есть два места, на каждое из которых может сесть 8 человек, из которых только одна девочка. Таким образом вероятность, что девочки будут сидеть рядом равна 2/8 = 0,25.
Ответ: 0,25.▲
Замечание. Вторая девочка может сесть лишь на 8 свободных стульев. и только 2 варианта сесть рядом с первой. 8-2=6 вариантов не сесть рядом.
Задание. За круглый стол на 17 стульев в случайном порядке рассаживаются 15 мальчиков и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть рядом.
▼ Посадим первую девочку за стол. Таким образом у нас останется 1 девочка и 16 стульев. Сесть она может только на два стула - по обе стороны от уже сидящей девочки. Отсюда вероятность того, что девочки сядут рядом:
2/16=1/8=0,125
Ответ: 0,125▲
Задание. За круглый стол на 9 стульев в случайном порядке рассаживаются 7 мальчиков и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть рядом.
▼ Допустим, что первая девочка уже села на какой-то определенный стул. Тогда, чтобы вторая девочка оказалась рядом с ней она должна сесть либо слева, либо справа от первой девочки. Имеем m=2 благоприятных исхода. Всего возможных исходов n=9-1=8 (так как первая девочка уже сидит на одном стуле). Таким образом, искомая вероятность, равна:
.Ответ: 0,25.
Замечание. Пусть первой за стол сядет девочка на любое из девяти мест, тогда рядом с ней есть два места, (m=2 — количество благоприятных вариантов), на каждое из которых претендует 8 человек (n=8 - общее количество вариантов).Таким образом, по формуле классической вероятности, вероятность того, что девочки будут сидеть рядом равна P=m/n=2/8=0,25.
Задание. В группе туристов 50 человек. Их микроавтобусом в несколько приёмов завозят к отправной точке маршрута по 10 человек за рейс. Порядок перевозки туристов случаен. Найдите вероятность того, что турист П отправится в первом рейсе микроавтобуса.
▼ Событие А – турист П отправится в первом рейсе микроавтобуса.
Общее число исходов турист П. отправится в первом рейсе микроавтобуса n = 50 (общее число мест), благоприятных исходов m = 10 (число мест на первом рейсе). Тогда
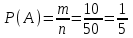= 0,2.Ответ: 0,2.▲
Задание. В группе туристов 30 человек. Их вертолётом в несколько приёмов забрасывают в труднодоступный район по 6 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист П. полетит первым рейсом вертолёта.
▼ Событие А – турист П полетим первым рейсом вертолета.
Общее число рейсов n = 30 : 6 = 5. Благоприятствующим будет только m = 1. Тогда
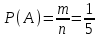= 0,2.Ответ: 0,2.▲
Задание. В классе 25 человек. С помощью жребия они выбирают трёх человек, которые должны пойти на митинг. Найдите вероятность того, что обучающийся в этом классе ученик К., пойдёт на митинг.
▼ Событие А – ученик К пойдет на митинг. Общее число исходов
n = 25, благоприятных исходов m = 3. Тогда
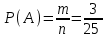= 0,12.Ответ: 0,12.▲
Пример 2. Фабрика выпускает сумки. В среднем из 100 сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
▼ Событие А – купленная сумка качественная. Всего n = 100 сумок. Качественных m = 100 – 8 = 92 сумок. Тогда
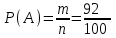= 0,92.Ответ: 0,92. ▲
Задание. Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
▼ Событие А – купленная сумка качественная. Всего n = 100 + 8 = 108 сумок (100 качественных и 8 с дефектами). Качественных m = 100 сумок. Тогда
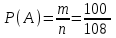= 0,93.Ответ: 0,93. ▲
Пример 3. В ящике 9 красных, 6 жёлтых и 5 зелёных шаров. Из ящика наугад достают один шар. Какова вероятность того, что этот шар окажется жёлтым?
▼ Событие А – шар окажется желтым. Общее число исходов n = 20. Благоприятствующих событию А исходов m = 6. Тогда
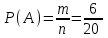= 0,3.Ответ: 0,3.▲
Задание. В ящике 2 зеленых, 3 красных и 5 синих шаров. Из ящика наугад достают один шар. Какова вероятность, что шар: а) зелёный; б) не зеленый ?
▼ Общее число исходов n = 10.
а) Событие А – шар окажется зеленым. Благоприятствующих событию А исходов m = 2. Тогда
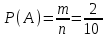= 0,2.б) Событие А – шар окажется не зеленым. Благоприятствующих событию А исходов m = 3 + 5 = 8. Тогда
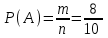= 0,8.Ответ: 0,2; 0,8.▲
Задание. Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже чем 36,8 °С, равна 0,81. Найдите вероятность того, что в случайный момент времени у здорового человека температура окажется 36,8 °С или выше.