ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 125
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
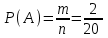= 0,1.Ответ: 0,1. ▲
Задание. В классе 16 учащихся, среди них два друга - Вадим и Сергей. Учащихся случайным образом разбивают на 4 равные группы. Найдите вероятность того, что Вадим и Сергей окажутся в одной группе.
▼ Событие А – Вадим и Сергей окажутся в одной группе. Если Вадиму первому досталось некоторое место, то Сергею остаётся n = 15 мест. Из них m= 3 - в той же группе, где Вадим. Искомая вероятность
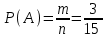= 0,2.Ответ: 0,2. ▲
Задание. На турнир по шахматам прибыло 26 участников в том числе Коля и Толя. Для проведения жеребьевки первого тура участников случайным образом разбили на две группы по 13 человек. Найти вероятность того, что Коля и Толя попадут в разные группы.
▼ Событие А – Коля и Толя попадут в разные группы. Всего 26 мест. Пусть Коля займет случайное место в любой группе. Останется n = 25 мест, из них в другой группе 13, в которую должен попасть Толя. Следовательно, число благоприятствующих событию А исходов m = 13. Тогда
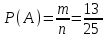= 0,52.Ответ: 0,52. ▲
Жеребьевка. Если в условии задачи сказано, что порядок определяется жребием в случайном порядке, то совершенно не важно, каким по счету должен выступать спортсмен (первым, последним или пятым).
Пример 9. В чемпионате участвуют 20 спортсменок: 8 из России, 7 из США, остальные – из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.
▼ Событие А – первой выступает гимнастка из Китая. Всего спортсменок n = 20. Благоприятствующих событию А исходов m = 5. Тогда
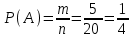= 0,25.Ответ: 0,25.▲
Задание. В соревнованиях по толканию ядра участвуют 4 спортсмена из Финляндии, 7 спортсменов из Дании, 9 спортсменов из Швеции и 5 – из Норвегии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий последним, окажется из Швеции.
▼ Событие А – последним выступает спортсмен из Швеции. Всего спортсменов n = 25. Благоприятствующих событию А исходов m = 9. Тогда
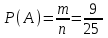
= 0,36.
Ответ: 0,36. ▲
Задание. На чемпионате по прыжкам в воду выступают 25 спортсменов, среди них 8 прыгунов из России и 9 прыгунов из Парагвая. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что шестым будет выступать прыгун из Парагвая.
▼ Событие А – шестым выступает прыгун из Парагвая. Всего спортсменов n = 25. Благоприятствующих событию А исходов m = 9. Тогда
= 0,36.Ответ: 0,36. ▲
Задание. Конкурс исполнителей проводится в 5 дней. Всего заявлено 80 выступлений – по одному от каждой страны. В первый день заявлено 8 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса?
▼ Событие А – выступление представителя России состоится в третий день. Всего n = 80 выступлений. В первый день 8 выступлений, в оставшиеся 5 – 1 = 4 дня по (80 – 8)/4 = 18 выступлений. Значит в третий день состоится 18 выступлений. Благоприятствующих событию А исходов m = 18. Тогда
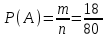= 0,225.Ответ: 0,225. ▲
Задание. Научная конференция проводится в 5 дней. Всего запланировано 75 докладов: первые три дня по 17 докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
▼ Событие А – доклад профессора М на последнем дне. Всего n = 75 докладов. В первый три дня по 17 докладов, в оставшиеся 5 – 3 = 2 дня по (75 – 51)/2 = 12 докладов. Значит в последний день состоится 12 докладов. Благоприятствующих событию А исходов m = 12. Тогда
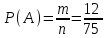= 0,16.Ответ: 0,16. ▲
Задание. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России?
▼ Событие А – Руслан Орлов будет играть с бадминтонистом из России. Соревнования по бадминтону обычно проводятся с выбыванием
, и только в первом туре участвуют все 26 бадминтонистов. Но число всех возможных исходов не равно 26, n = 26 – 1 = 25, потому что Руслан Орлов не может играть с самим собой. По той же причине m = 10 – 1 = 9, ведь Руслан Орлов входит в число 10 участников. Тогда
= 0,36.Ответ: 0,36. ▲
Задание. Перед началом первого тура чемпионата по настольному теннису участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 16 спортсменов, среди которых 7 участников из России, в том числе Платон Карпов. Найдите вероятность того, что в первом туре Платон Карпов будет играть с каким-либо спортсменом из России?
▼ Событие А – Платон Карпов будет играть с каким-либо спортсменом из России. Но число всех возможных исходов не равно 16, n = 16 – 1 = 15, потому что Платон Карпов не может играть с самим собой. По той же причине m = 7 – 1 = 6, ведь Платон Карпов входит в число 7 участников. Тогда
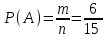= 0,4.Ответ: 0,4. ▲
Задание. В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?
▼ Событие А – команда России во второй группе. Общее число исходов n = 16 (16 карточек). Число благоприятствующих событию А исходов m = 4 (четыре карточки с номером 2). Тогда
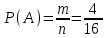= 0,25.Ответ: 0,25. ▲
Задачи на теоремы о вероятностях событий
Теорема произведения независимых событий
Пример 10. Вероятность того, что батарейка бракованная, равна 0,06. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.
▼ Пусть А, В – события, что соответствующая батарейка исправна. По условию Р(А) = Р(В) = 1 - 0,06 = 0,94. События А, В – независимые. Тогда вероятность, что обе батарейки окажутся исправными
= 
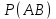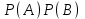
= 0,94∙0,94 = 0,8836.
Ответ: 0,8836. ▲
Задание. Вероятность того, что ручка бракованная, равна 0,05. Покупатель в магазине приобретает случайную упаковку, которая содержит две ручки. Найдите вероятность того, что обе ручки в этой упаковке окажутся исправными.
▼ События А, В – соответствующая ручка исправная. По условию P(A) = P(B) = 1- 0,05 = 0.95. События А, В – независимые. Тогда вероятность, что обе ручки исправные
P(AB) = P(A)⋅P(B) = 0,95⋅0,95= 0,9025.
Ответ: 0,9025▲
Задание. Вероятность того, что аккумулятор не заряжен, равна 0,15. Покупатель в магазине приобретает случайную упаковку, которая содержит два таких аккумулятора. Найдите вероятность того, что оба аккумулятора в этой упаковке окажутся заряжены.
▼ События А, В – соответствующий аккумулятор заряжен. По условию P(A) = P(B) = 1- 0,15 = 0.85. События А, В – независимые. Тогда вероятность, что оба аккумулятора в этой упаковке окажутся заряжены
P(AB) = P(A)⋅P(B) = 0,85⋅0,85= 0,7225.
Ответ: 0,7225▲
Задание. Какова вероятность того, что случайно выбранный телефонный номер оканчивается двумя чётными цифрами?
▼ Пусть А, В – события, что на одном из требуемых мест окажется чётное число. По условию Р(А) = Р(В) = 0,5. События А, В – независимые. Тогда вероятность того, что на двух местах одновременно окажутся два чётных числа
= 
= 0,5∙0,5 = 0,25.Ответ: 0,25. ▲
Задание. Ответ: 0,156
В магазине три продавца. Каждый из них занят с клиентом с вероятностью 0,3. Найдите вероятность того, что в случайный момент времени все три продавца заняты одновременно (считайте, что клиенты заходят независимо друг от друга).
▼ Пусть А1, А2, А3 – события, что соответствующий продавец занят. По условию, Р(А1) = Р(А2) = Р(А3) = 0,3. События А1, А2, А3 – независимые. Тогда вероятность того, что все три продавца заняты одновременно
= 
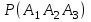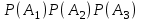= (0,3)3 = 0,027.Ответ: 0,027. ▲
Задание . Ответ: 0,88
Ответ: 0,75
Ответ: 0,2
61616661.66Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд будет первой владеть мячом. Команда А должна сыграть два матча - с командой В и с командой С. Найдите вероятность того, что в обоих матчах первой мячом будет владеть команда А.
▼ Вероятность того, что команда А будет первая владеть мячом в одном матче составляет 1/2, а в двух матчах: (1/2)2 = 0,25.
Ответ: 0,25. ▲
Задание. Ответ: 0,88
Ответ: 0,75
Ответ: 0,2
61616661.66Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд будет первой владеть мячом. Команда А должна сыграть три матча - с командой В, с командой С и с командой D. Найдите вероятность того, что во всех матчах первой мячом будет владеть команда А.
▼ Вероятность того, что команда А будет первая владеть мячом в одном матче составляет 1/2, а в трех матчах: (1/2)3 = 0,125.
Ответ: 0,125. ▲
Задание. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.
▼ Событие А - биатлонист попал в мишень. По условию, вероятность попадания Р(А) = 0,8, тогда вероятность промахнуться Р(
