ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 126
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
▼ Указанные события противоположны, поэтому искомая вероятность равна 1 − 0,81 = 0,19.
Ответ: 0,19.▲
Задание. На фабрике керамической посуды 10% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 80% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Результат округлите до сотых.
▼ Пусть завод произвел х тарелок. В продажу поступят все качественные тарелки и 20% не выявленных дефектных тарелок: 0,9х + 0,2∙0,1х = 0,92х тарелок.
Поскольку качественных из них 0,9х, вероятность купить качественную тарелку равна
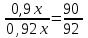≈ 0,98.Ответ: 0,98. ▲
Пример 4. Монета подбрасывается один раз. Найти вероятность выпадения герба.
▼ Пусть А – искомое событие.
Исходы: {Г, Р}, n = 2.
Благоприятные: А = {Г}, m = 1. Тогда
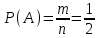= 0,5.Ответ: 0,5.▲
Пример 5. Монета подбрасывается два раза. Найти вероятность, что герб выпадет: а) ни разу; б) хотя бы один раз; в) только один раз.
▼ Исходы: {ГГ, ГР, РГ, РР}, n = 22 = 4.
а) Благоприятные: А1 = {РР}, m = 1. Тогда
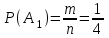= 0,25.б) Благоприятные: А2 = {ГГ, ГР, РГ}, m = 3. Тогда
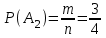= 0,75, или так: 
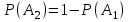= 1 – 0,25 = 0,75.в) Благоприятные: А3 = {ГР, РГ}, m = 2. Тогда
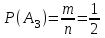= 0,5.Ответ: 0,25; 0,75; 0,5.▲
Задание. Монета подбрасывается три раза. Найти вероятность, что герб выпадет: а) ни разу; б) хотя бы один раз; в) только один раз.
▼ Составим таблицу всех возможных исходов
| 1 бросание | Г | Р |
| 2 бросание | Г | Р |
| 3 бросание | Г | Р |
Общее число исходов: n = 23 = 8.
а) Благоприятные: А1 = {РРР}, m = 1. Тогда
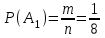= 0,125.б) Благоприятные:
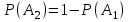
= 1 – 0,125 = 0,875.
в) Благоприятные: А3 = {ГРР, РГР, РРГ}, m = 3. Тогда
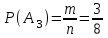= 0,375.Ответ: 0,125; 0,875; 0,375.▲
Задание. Монета подбрасывается четыре раза. Найти вероятность, что герб выпадет: а) ни разу; б) хотя бы один раз; в) только один раз.
▼ Составим таблицу всех возможных исходов
| 1 бросание | Г | Р |
| 2 бросание | Г | Р |
| 3 бросание | Г | Р |
| 4 бросание | Г | Р |
Общее число исходов: n = 24 = 16.
а) Благоприятные: А1 = {РРРР}, m = 1. Тогда
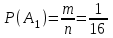= 0,0625.б) Благоприятные:
= 1 – 0,0625 = 0,9375.в) Благоприятные: А3 = {ГРРР, РГРР, РРГР, РРРГ}, m = 4. Тогда
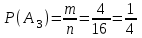= 0,25.Ответ: 0,0625; 0,9375; 0,25.▲
Пример 6. Найти вероятность, что при одном бросании игральной кости выпадет число очков, кратное двум.
▼ Пусть А – искомое событие.
Исходы: {1, 2, 3, 4, 5, 6}, n = 6.
Благоприятные: А = {2, 4, 6 }, m = 3. Тогда
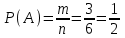= 0,5.Ответ: 0,5.▲
Задание. Найти вероятность, что при одном бросании игральной кости выпадет число очков, кратное трем.
▼ Пусть А – искомое событие.
Исходы: {1, 2, 3, 4, 5, 6}, n = 6.
Благоприятные: А = {3, 6 }, m = 2. Тогда
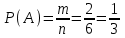≈ 0,33.Ответ: ≈ 0,33.▲
Задание. Таня и Маша бросают кубик по одному разу. Выигрывает тот, кто выбросил больше очков. Если количество очков совпадает, это ничья. Найдите вероятность того, что Маша проиграла, если в сумме у них выпало 8 очков.
▼ Составим таблицу всех возможных исходов
| Таня | 1 | 2 | 3 | 4 | 5 | 6 |
| Маша | 1 | 2 | 3 | 4 | 5 | 6 |
Исходы: (2, 6), (3, 5), (4, 4), (5, 3), (6, 2), n = 5.
Благоприятные: (5, 3), (6, 2), m = 2.
Вероятность, что Маша проиграла: 2/5 = 0,4.
Ответ: 0,4. ▲
Задание. Галя дважды бросила игральный кубик. Известно, что в сумме у неё выпало 9 очков. Найдите вероятность, что при втором бросании выпало 6 очков.
▼ Составим таблицу всех возможных исходов
| 1 бросок | 1 | 2 | 3 | 4 | 5 | 6 |
| 2 бросок | 1 | 2 | 3 | 4 | 5 | 6 |
Исходы: (3, 6), (4, 5), (5, 4), (6, 3), n = 4.
Благоприятные: (3, 6),
m = 1.
Искомая вероятность: 1/4 = 0,25.
Ответ: 0,25. ▲
Задание. Какова вероятность, что сумма очков, выпавших на двух брошенных костях, равно 5.
▼ Пусть А – искомое событие. Составим таблицу
| 1 бросание | 1 | 2 | 3 | 4 | 5 | 6 |
| 2 бросание | 1 | 2 | 3 | 4 | 5 | 6 |
Общее число исходов n = 62 = 36.
Благоприятные: А = {(1, 4), (2, 3), (3, 2), (4, 1) }, m = 4. Тогда
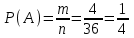= 0,25.Ответ: 0,25.▲
Задание. Дважды бросается игральный кубик. Какова вероятность того что оба раза выпадет число 5.
▼ Пусть А – искомое событие. Составим таблицу
| 1 бросание | 1 | 2 | 3 | 4 | 5 | 6 |
| 2 бросание | 1 | 2 | 3 | 4 | 5 | 6 |
Общее число исходов n = 62 = 36.
Благоприятные: А = {(5, 5)}, m = 1. Тогда
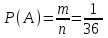≈ 0,028.Ответ: ≈ 0,028.▲
Пример 7. Из множества натуральных чисел от 10 до 19 выбирают одно число. Какова вероятность, что оно делится на 3?
▼ Выпишем в ряд заданные числа и отметим те из них, которые делятся на 3:
10, 11, 12, 13, 14, 15, 16, 17, 18, 19.
Получили, что из n = (19 – 10 + 1) = 10 заданных чисел на 3 делятся m = 3 числа. Тогда
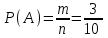= 0,3.Ответ: 0,3. ▲
Замечание. На 3 делится каждое третье число в натуральном ряде, на 4 – каждое четвертое, на 5 – каждое пятое, и т.д.
Задание. Из множества натуральных чисел от 107 до 198 выбирают одно число. Какова вероятность, что оно делится на 3?
▼ Определим количество групп из трех чисел на участке от 107 до 198. На этом участке всего n = (198 – 107 + 1) = 92 числа. Они составляют 30 полных групп и одну неполную (92/3 = 30 целых и 2 в остатке). В каждой полной группе есть одно число, которое делится на 3. В неполной группе, которую составляют два последних числа, 197 не делится на 3, а 198 делится. Итого, благоприятствующих чисел
m = 30 +1 = 31. Тогда
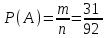≈ 0,337.Ответ: ≈ 0,337. ▲
Задание. Коля выбирает трехзначное число. Найдите вероятность того, что оно делится на 5.
▼ Событие А – выбранное число делится на 5. Всего трехзначных чисел n = 999 – 100 + 1 = 900. На пять делится каждое пятое их них, т.е. таких чисел m = 900:5=180. Тогда
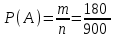= 0,2.Ответ: 0,2. ▲
Задание. Ответ: 0,25Ответ: 0,75Ответ: 0,052929Для экзамена подготовили билеты с номерами от 1 до 50. Какова вероятность того, что наугад взятый учеником билет имеет однозначный номер?
▼ Событие А – взятый билет имеет однозначный номер. Всего было подготовлено n = 50 билетов, среди которых m = 9 были однозначными. Тогда
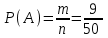= 0,18.Ответ: 0,18. ▲
Пример 8. В классе 26 учащихся, среди них два друга - Сергей и Андрей. Учащихся случайным образом разбивают на 2 равные группы. Найдите вероятность того, что Сергей и Андрей окажутся в одной группе.
▼ Событие А – Сергей и Андрей окажутся в одной группе. Если Сергею первому досталось некоторое место, то Андрею остаётся n = 25 мест. Из них m= 12 - в той же группе, где Сергей. Искомая вероятность
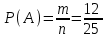= 0,48.Ответ: 0,48. ▲
Задание. В классе 21 учащихся, среди них два друга - Вадим и Олег. Класс случайным образом разбивают на 3 равные группы. Найдите вероятность того, что Вадим и Олег окажутся в одной группе.
▼ Событие А – Вадим и Олег окажутся в одной группе. Если Вадиму первому досталось некоторое место, то Олегу остаётся n = 20 мест. Из них m= 6 - в той же группе, где Вадим. Искомая вероятность
= 0,3.Ответ: 0,3. ▲
Задание. В классе 21 учащийся, среди них две подруги - Аня и Нина. Класс случайным образом делят на семь групп, по 3 человека в каждой. Найдите вероятность того, что Аня и Нина окажутся в одной группе.
▼ Событие А – Аня и Нина окажутся в одной группе. Если Ане первой досталось некоторое место, то Нине остаётся n = 20 мест. Из них m= 2 - в той же группе, где Аня. Искомая вероятность