Индивидуальная практическая работа 2. Динамическое программирование.

Указания по выбору варианта

Выбор вариантов контрольного задания осуществляется студентом самостоятельно на основании двух последних цифр номера зачетной книжки (в каждом задании предусмотрено 20 вариантов).
Варианты
Задача (1-2) о распределении средств между предприятиями

Планируется деятельностьnпромышленныхпредприятий на очередной год. Начальные средства: s₀ . Размеры вложений в каждое предприятие кратныx . Средства x , выделенные предприятию i приносят в конце года прибыльf_i (x), i = 1,2. … n.

Прибыльf_i (x) не зависит от вложения средств в другие предприятия. Прибыль от каждого предприятия выражается в одних и тех же условных единицах; суммарная прибыль равна сумме прибылей от каждого предприятия.

Определить, какое количество средств нужно выделить каждому предприятию, чтобы суммарная прибыль была наибольшей.

Задача (3-4) об оптимальном распределении ресурсов между отраслями на n лет

Планируется деятельность производства на n лет. Начальные ресурсы: s₀ . Средства x , вложенные в отрасль 1 в начале года, дают в конце года прибыль f₁(x) и возвращаются в размере ₁(x)< x. Для отрасли 2 аналогично - f₂(x) и ₂ (x)< x. В конце года все возвращенные средства заново перераспределяются между этими отраслями, новые средства не поступают, прибыль в производство не вкладывается.

Требуется распределить имеющиеся средства между двумя отраслями производства на лет так, чтобы суммарная прибыль от обеих отраслей за n лет была максимальной.
В задачах 1-2 найти оптимальное распределение средств между предприятиями при условии, что прибыль f(x), полученная от каждогопредприятия, является функцией от вложенных в него средств x, вложения кратны x , а функция f(x) заданы таблично.

---

Задача 1

x	1	2	3	4	5	6	7	8	9
f1(x)	5	9	12	14	15	18	20	24	27
f2(x)	7	9	11	13	16	19	21	22	25
f3(x)	6	10	13	15	16	18	21	22	25
f4(x)	3	5	7	11	13	15	20	22	24

s₀ = 9, x = 1, n= 4(3)
Задача 2.

x	1	2	3	4	5
f1(x)	0,2	0,9	1,0	1,2	2,0
f2(x)	1,0	1,1	1,3	1.4	1,8
f3(x)	2,1	2,5	2,9	3,9	4,9
f4(x)	0	2,0	2,5	3,0	4,0

s₀ = 5, x = 1, n= 4
В задачах 3-4 найти оптимальное распределение ресурсов

---

s₀ между двумя отраслями производства в течение n лет, если даны функции доходов f₁(x) f₂(x) для каждой отрасли, функции возврата ₁(x) и ₂ (x). По истечении года только все возвращенные средства перераспределяются, доход в производство не вкладывается

Задача 3. s₀= 40000 ед.; n= 4; f₁(x)=0.4 x; f₂(x)=0.3 x;₁(x)=0.5 x;₂ (x)=0.8 x

Задача 4. s₀= 10000 ед.; n= 4; f₁(x)=0.4 x²; f₂(x)=0.5x;₁(x)=0.75 x;₂ (x)=0.3 x
Варианты индивидуального задания

номер варианта	Условия задания
2.1	Решить задачу 1
2.2	В условиях задачи 1 принять s0 = 8, n= 3, x = 2
2.3	В условиях задачи 1 принять s0 = 8. n= 3
2.4	Решить задачу 1 при n= 4, x = 2
2.5	В условиях задачи 1 принять s0 = 8 и найти оптимальное распределение средств между 2-,3- и 4-м предприятиями
2.6	В условиях задачи 1 принять s0 = 9, n= 3, x = 3
2.7	В условиях задачи 1 принять s0 = 9, n= 4, x = 3
2.8	Решить задачу 2
2.9	В условиях задачи 2 принять s0 = 4
2.10	В условиях задачи 2 принять s0 = 6, x = 2
2.11	В условиях задачи 1 принять s0 = 10, x = 2
2.12	Решить задачу 3
2.13	В условиях задачи 3 принять s0 = 20000 ед.
2.14	В условиях задачи 3 принять s0 = 30000 ед.
2.15	Решить задачу 4
2.16	В условиях задачи 4 принять s0 = 20000 ед.
2.17	В условиях задачи 4 принять s0 = 30000 ед.
2.18	Решить задачу 3 при условии, что в начале каждого года дополнительно поступают средства с размерах s= 10000
2.19	Решить задачу 4 при условии, что в начале каждого года дополнительно поступают средства с размерах s= 2000
2.20	Решить задачу 1 при n= 3

---

Методические указания

Динамическое программирование (ДП) – метод оптимизации, приспособленный к операциям, в которых процесс принятия решения может быть разбит на этапы (шаги). Такие операции называются многошаговыми.

Показатель эффективности данной управляемой операции – целевая функция – зависит от начального состояния и управления Z = F(₀,X).

Целевая функция является аддитивной от показателей эффективности Z_n каждого шага Z= 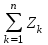= 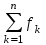(_k–1,x_k), k = 1, 2,…,nи управления состоянием _n= _k(_k–1, x_k), k =1, 2,…,n.

Задача пошаговой оптимизации (задача ДП) формулируется так: определить такое допустимое управление X (Х₁, Х₂,…,Х_n), переводящее систему Sиз состояния ₀ в состояние 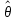, при котором целевая функция Zпринимает наибольшее (наименьшее) значение.

Вычислительная схема ДП связана с принципом оптимальности Беллмана и использует рекуррентные соотношения.

Z_k*(_k–1) = 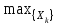{f_k(_k–1, X_k)+ Z_k+1*(_k)}, k=1,2,…,n–1. (2.1)

Согласно принципу оптимальности, X_kвыбирается из условия максимума этой суммы.

В результате условной оптимизации получаются две последовательности:

– Z_n*(_n–1), Z_n–1*(_n–2),…,Z₂*(₁), Z₁*(₀) – условные максимумы целевой функции на последнем, на двух последних,…, на n шагах;

– X_n*(_n–1), X_n–1*(_n–2),…,X₂*(₁), X₁*(₀) – условные оптимальные управления на n–м, (n–1) –м,…,1–м шагах.
2.1. Задача о распределении средств между предприятиями

---

Планируется деятельность четырех промышленных предприятий на очередной год. Начальные средства: ₀ = 5 у.е. Размеры вложения в каждое предприятие кратны 1 у.е. Средства x, выделенные k–му предприятию (k = 1, 2, 3, 4), приносят в конце года прибыль f_k(x). Функции f_k(x) заданы таблично.
Таблица 2.1

x	f1(x)	f2(x)	f3(x)	f4(x)
1	8	6	3	4
2	10	9	4	6
3	11	11	7	8
4	12	13	11	13
5	18	15	18	16

Будем считать, что:

• 
  прибыль f_n(x) не зависит от вложений средств в другие предприятия;
  
• 
  прибыль от каждого предприятия выражается в одних и тех же условных единицах;
  
• 
  суммарная прибыль равна сумме прибылей, полученных от каждого предприятия.
  

Определить, какое количество средств нужно выделить каждому предприятию, чтобы суммарная прибыль была наибольшей.
Решение. Обозначим через x_kколичество средств, выделенных k–му предприятию. Суммарная прибыль равна

Z= 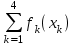. (2.2)

Переменные x_k удовлетворяют ограничениям

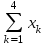=5, x_k  0, k = 1, 2, 3, 4. (2.3)

Требуется найти переменные x₁, x₂,, x₃,, x₄, удовлетворяющие (6.3) и обращающие в максимум функцию (6.2).

Схема решения задачи ДП: процесс решения распределения средств ₀ = 5 можно рассматривать как четырехшаговый, номер шага совпадает с номером предприятия; выбор переменных x₁, x₂, x₃, x₄– управление соответственно на 1, 2, 3 и 4 шагах; —конечное состояние процесса распределения – равно 0, т.к. все средства должны быть вложены. Схема распределения показана на рис. 6.1.

---

Смотрите также файлы

• 1 Теоретические основы развития регионального туризма.docx

• "Подведомственность и подсудность гражданских дел.".doc

• Таким образом, созданная система обладает набором необходимых функций.docx

• Моя малая родина.doc

• Методические рекомендации по изучению дисциплинам Деловая коммуникация.doc