Рис. 2.1
Уравнения состояний в данной задаче имеют вид _k = _k–1– x_k, k=1, 2, 3, 4, где _k – параметр состояния – количество средств, оставшихся после k–го шага, т.е. средства, которые остается распределить между оставшимися 4–k предприятиями.

Z_k*(_k–1) – условная оптимальная прибыть, полученная от k–го, (k+1)–го, …, 4 предприятий, если между ними оптимальным образом распределялись средства _k–1. Допустимые управления на k–м шаге удовлетворяют условию 0  х_k_k–1.

Уравнения Беллмана имеют вид:

к = 4, ₄=0  Z₄*(₃)=max f₄(x₄), 0  x₄₃;

Z₃*(₂)=max {f₃(x₃) + Z₄*(₃)}, 0  x₃₂;

Z₂*(₁)=max {f₂(x₂) + Z₃*(₂)}, 0  x₂₁;

Z₁*(5)=max {f₁(x₁) + Z₂*(₁)}, 0  x₃ 5.

4 шаг (k = 4). В табл. 2.1 f₄(x) прибыли монотонно возрастают, поэтому все средства, оставшиеся к IV шагу, следует вложить в 4–е предприятие. Для возможных значений ₃ = 0, 1, 2, 3, 4, 5 получим Z₄*(₃)=f₄(₃) и x₄*(₃)=₃.
Таблица 2.2

k–1	xk	k	k=3				k=2				k=1
			f3(x3)+ Z4*(3)	Z3*(2)	x3*(2)	f2(x2)+ Z3*(2)		Z2*(1)	x2*(1)	f1(x1)+ Z2*(1)		Z1*(0)	x1*(0)
1	2	3	4	5	6	7		8	9	10		11	12
0	0	0	0	0	0	0		0	0	0		0	0
1	0 1	1 0	0+4=4 3+0=3	4	0	0+4=4 6+0=6		6	1	0+6=6 8+0=8		8	1
2	0 1 2	2 1 0	0+6=6 3+4=7 4+0=4	7	1	0+7=7 6+4=10 9+0=9		10	1	0+10=10 8+6=14 10+0=10		14	1
3	0 1 2 3	3 2 1 0	0+8=8 3+6=9 4+4=8 7+0=7	9	1	0+9=9 6+7=13 9+4=13 11+0=11		13	1 2	0+13=13 8+10=18 10+6=16 11+0=11		18	1
4	0 1 2 3 4	4 3 2 1 0	0+13=13 3+8=12 4+6=10 7+4=11 11+0=11	13	0	0+13=13 6+9=15 9+7=16 11+4=15 13+0=13		16	2	0+16=16 8+13=21 10+10=20 11+6=17 12+0=12		21	1
5	0 1 2 3 4 5	5 4 3 2 1 0	0+16=16 3+13=16 4+8=12 7+6=13 11+4=16 18+0=18	18	5	0+18=18 6+13=19 9+9=18 11+7=18 13+4=17 15+0=15		19	1	0+19=19 8+16=24 10+13=23 11+10=21 12+6=18 18+0=18		24	1

---

3 шаг (k = 3). Делаем все предположения относительно остатка средств ₂ к 3 шагу, т.е. после выбора x₁ и x₂. ₂ = 0, 1, 2, 3, 4, 5 (0 – все средства отданы 1 и 2–му предприятиям, 5 – 1–е и 2–е предприятия ничего не получили и т.д.) В зависимости от этого выбираем 0  x₃₂, находим ₃=₂ – x₃и сравниваем для разных x₃при фиксированном ₂ значения суммы f₃(x₃)+Z₄*(₃). Для каждого ₂наибольшее из этих значений есть Z₃*(₂) – условная оптимальная прибыль, полученная при оптимальном распределении ₂ между 3–м и 4–м предприятиями. Оптимизация приведена в табл. 6.2 при k = 3.

2 шаг. Условный оптимум приведен в той же таблице и для k = 2. Для всех возможных значений ₂значения Z₂*(₁) и Х₂*(₁) находятся в столбцах 8 и 9 соответственно; первые слагаемые в столбце 7 – значения f₂(x₂) взяты из табл. 6.2, а вторые слагаемые взяты из столбца 5 табл. 6.2 при ₂=₁–x₂.

1 шаг. Условный оптимум приведен и для k = 1 при ₀ = 5.

Итак, максимум суммарной прибыли Z_max=Z₁*(5)=24 у. е. при

x₁*=x₁*(5)=1

 ₁*=5–1=4  x₂*=x₂*(4)=2 

 ₂*=4–2=2  x₃*=x₃*(2)=1 

 ₃*=2–1=1  x₄*=x₄*(1)=₃*=1.

Выделение средств различным предприятиям:

1–му выделена 1 у. е.

2–му выделены 2 у. е.

3–му выделена 1 у. е.

4–му выделена 1 у. е.

Замечания.

Решение четырехмерной задачи на определение условного экстремума сведено фактически к решению четырех одномерных задач: на каждом шаге определялась одна переменная х.

Из разобранной задачи видно, что метод ДП безразличен к виду и способу задания функции: f_k(x) были заданы таблично, поэтому Z_k*() и Х_k*() принимали дискретные значения, представленные в таблице.

Достоинством метода является возможность анализа решения на чувствительность к изменению ₀

---

и n. Проведенные расчеты можно использовать для изменившихся начального состояния ₀ и числа шагов n. Например, пусть в задаче произошло уменьшение начальных средств на 1 у.е. Для ₀ = 4 достаточно в таблицу добавить расчеты при k= 1. Получаем в этом случае Z_max = 21 у.е. при распределении:

x₁*=1₁*=4–1=3  x₂*=1, или x₂*=2

₂*=3–1=2, или ₂*=3–2=1 x₃*=1, или x₃*=0 

₃*=2–1=1, или₃*=1–0=1,  x₄*=1.

В результате найдены два оптимальных решения: (1,1,1,1) и (1,2,0,1). Если начальные средства увеличились, например, на 1 у.е., ₀ = 6, а функции прибыли f_k(x) остались прежними, то в таблицу достаточно добавить раздел для ₀ = 6 при k= 3, 2, 1; этот фрагмент расчетов помещен в табл. 2.3.

Таблица 2.3

6

0 1 2 3 4 5

6 5 4 3 2 1

0+0=0 3+16=19 4+13=17 7+8=15 11+6=17 18+4=22

22

5

0+22=22 6+18=24 9+13=22 11+9=20 13+7=20 15+4=19

24

1

0+24=24 8+19=27 10+16=26 11+13=24 12+10=22 18+6=24

27

1

Получаем Z_max=27 у.е. при распределении:

x₁*=1₁*=6–1=5  x₂*=1₂*=5–1=4 x₃*=0 ₃*=4–0=4 x₄*=4.

Оптимальное решение (1,1,0,4).

Если принято решение распределить средства ₀ = 5 между 2–, 3– и 4–м предприятиями, то задача уже решена. В разделе k= 2 табл. 6.2 находим Z_max=Z₂*(5)=19 при условии, что x₂*=1, x₃*=0, x₄*=4.

Наконец, если увеличилось количество предприятий (число шагов), то схему можно дополнить, присоединяя шаги с номерами k= 0,–1,… и т.д. Например, пусть средства в размере 6 у.е. распределяются между пятью предприятиями. Функция прибыли для пятого предприятия задана формулой f(x) = 3x+1, если х   и f(0) = 0. Присвоим 5–му предприятию номер

---

k= 0, тогда х₀ = 0 – средства, выделенные этому предприятию. Обозначим через Z₀*(6) оптимальную прибыль, полученную от пяти предприятий:

Z₀*(6)= Z₃*(₂)=max {f₀(x₀) + Z₁*(₁)}, 0  x₀ 6,

а ₁= 6 – х₀. Условная оптимизация 0–го шага дана в табл. 2.4.

Таблица 2.4

x0	0	1	2	3	4	5	6
1= 6 – х0	6	5	4	3	2	1	0
f(0) = 0	0	4	7	10	13	16	19
Z1*(1)(приk=1)	27	24	21	18	14	8	0
f(x0) + Z1(1)	27	28	28	28	27	24	19

Следовательно, Z_max=28, а оптимальных решений четыре: (1,1,2,1,1), (2,1,1,1,1), (2,1,2,0,1), (3,1,1,0,1). ▼

1. 
   2.2. Задача об оптимальном распределении ресурсов между отраслями
   

на n лет
Планируется деятельность двух отраслей производства на n лет. Начальные ресурсы ₀. Средства х, вложенные в 1–ю отрасль в начале года, дают в конце года прибыль f₁(x) и возвращаются в размере q₁(x) аналогично для 2–й отрасли функция прибыли равна f₂(x), а возврата — q₂(x) (q₂(x) В конце года все возвращенные средства заново перераспределяются между 1 и 2 отраслями, новые средства не поступают, прибыль в производство не вкладывается.

Требуется распределить имеющиеся средства ₀ между двумя отраслями производства на n лет так, чтобы суммарная прибыль от обеих отраслей за n лет оказалась максимальной.

Необходимо:

1. 
   построить модель ДП для задачи и вычислительную схему;
   
2. 
   решить задачу при условии, что ₀ = 10000 у.е., n = 4, f₁(x) = 0,6x, q₁(x) = 0,7x, f₂(x) = 0,5x, q₂(x) = 0,8x.
   

Решение. Процесс распределения средств между двумя отраслями производства разворачивается во времени, решения принимаются в начале каждого года, следовательно, осуществляется деление на шаги: номер шага – номер года. Управляемая система – две отрасли производства, а управление состоит в выделении средств каждой отрасли в очередном году. Параметры состояния к началу k–го года — _k–1 (k = 1,…,n) – количество средств, подлежащих распределению. Переменных управления на каждом шаге две: х_k — количество средств, выделенных 1 отрасли, и y_k — 2 отрасли. Но так как все средства _k–1 распределяются, то у_k = _k–1 – x_k, и поэтому управление на k–м шаге зависит от одной переменной x_n, т.е. Х_k (х_k, _k–1 – x_k).

Уравнения состояний выражают остаток средств, возвращенных в конце k–го года _k = q₁(x_k) + q₂(_k–1 – x_k).

Показатель эффективности k–го шага — прибыль, полученная в конце k–го года от обеих отраслей: f₁(x_k) + f₂(_k–1 – x_k).

Суммарный показатель эффективности — целевая функция задачи — прибыль за n лет: Z = 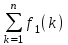+ f₂(_k-1 - x_k).

Пусть Z^*_k(_k–1) — условная оптимальная прибыль за n – k + 1 лет, начиная с k–го года до n–го года включительно, при условии, что имеющиеся на начало k–го года средства _k–1 в дальнейшем распределялись оптимально. Тогда оптимальная прибыль за n лет Z_max = Z^*₁(₀).

Уравнения Беллмана имеют вид:

Z^*_n(_n–1) = max {f₁(x_n) + f₂(_n–1 – х_n)},0 х_n_n–1;

Z^*_k(_k–1) = max {f₁(x_k) + f₂(_k–1 – х_k) + Z^*_k+1(_k)} , 0 х_k_k–1,

(k = n–1, n–2, …, 2).

Используем конкретные данные.

Уравнение состояний примет вид

_k = 0,7x_k + 0,8(_k–1 – x_k) или _k = 0,8_k–1 –0,1x_k.

Целевая функция k–го шага 0,6x_k + 0,5(_k–1 – x_k) = 0,1x_k + 0,5_k–1.

Целевая функция задачи Z = 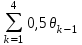+ 0,1x_k..

Z^*₄(₃) = max {0,5₃ + 0,1x₄} 0 х₄₃;

Z^*_k(_k–1) = max {0,1x_k + 0,5_k–1 + Z^*_k+1(_k)}, 0 х_k_k–1.



Проводим условную оптимизацию.




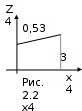
4 шаг. Используем уравнение Z^*₄(₃) = max {0,5₃ + 0,1x₄},0 х₄₃. Обозначим Z₄ = 0,1х₄ + 0,5₃; Z₄ линейная, возрастающая, так как угловой коэффициент 0,1 больше нуля. Поэтому максимум достигается на конце интервала [0;₃]. Следовательно, Z^*₄(₃)= 0,6₃ при х^*₄(₃)= ₃.

3 шаг. Уравнение Z^*₃(₂) = max {0,1x₃ + 0,5₂ + 0,6₃}, 0 х₃₂.

Найдем ₃ из уравнений состояний: ₃ = 0,8₂ – 0,1x₃ и, подставив его выражение в правую часть уравнения, получим

Z^*₃(₂) = max {0,1x₃ + 0,5₂ + 0,6(0,8₂ – 0,1x₃)} = max {0,04x₃ + 0,98₂}, 0 х₃₂.

Как и в предыдущем случае, максимум достигается при х₃=₂; т.е. Z^*₃(₂)= 1,02₂ при х^*₃(₂)= ₂.



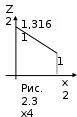
2 шаг. Из уравнения состояния: ₂ = 0,8₁ – 0,1x₂. Уравнение при k=2 примет вид Z^*₂(₁) = max {1,316₁ – 0,002x₂}, 0 х₂₁. Линейная функция Z^*₂ = 1,316₁ – 0,002x₂ относительно х₂ убывает на отрезке [0;₁], и поэтому ее максимум достигается при х₂=0: Z^*₂(₁)= 1,316₁ при х^*₂(₁)= 0.


1 шаг. ₁ = 0,8₁ – 0,1x₁. Уравнение при k=1 имеет вид

Z^*₁(₀) = max {1,5528₀ – 0,031x₁}, 0 х₁₀.

Как и в предыдущем случае, максимум достигается в начале отрезка, т.е. Z^*₁(₀)= 1,5528₀ при х^*₁(₀)= 0.

На этом условная оптимизация заканчивается. Используя ее результат и исходные данные, получим Z_max = Z^*₁(10000), Z_max = 15528.

х^*₁ = 0, у^*₁ = ₀ = 10000 

^*₁ = 0,8*10000 –0,1*0 = 8000  х^*₂ = 0, у^*₂ = 8000 

^*₂ = 0,8*8000 –0,1*0 = 6400  х^*₃ = 6400, у^*₃ =0 

^*₃ = 0,8*6400 –0,1*6400 = 4480  х^*₄ = 4480, у^*₄ =0.

Оптимальная прибыль за 4 года, полученная от двух отраслей производства при начальных средствах 10000 у.е., равна 15528 у.е. при условии, что 1 отрасль получает по годам (0;0;6400;4480), а 2 отрасль – соответственно (10000;8000;0;0).

---

Смотрите также файлы

• 1 Теоретические основы развития регионального туризма.docx

• "Подведомственность и подсудность гражданских дел.".doc

• Таким образом, созданная система обладает набором необходимых функций.docx

• Моя малая родина.doc

• Методические рекомендации по изучению дисциплинам Деловая коммуникация.doc