Файл: Отчет по заданию 1 Задание 1.docx

	HE x1 /\ HE x2 /\ x3	НЕ х1 /\ х2 /\ НЕ х3	х1 /\ НЕ х2 /\ НЕ х3	х1 /\ НЕ х2 /\ х3
НЕ х2 /\ х3	1			1
x1 /\ HE x2			1	1

Ядро: x1 /\ HE x2 \/ НЕ х2 /\ х3

Ядро + дополнение: x1 /\ HE x2 \/ НЕ х2 /\ х3 \/ HE x1 /\ x2 /\ HE x3

Метод Мак-Класки

	Члены f(x1, x2, x3)	Результаты 1-го склеивания	Результаты 2-го склеивания
1.	001	-01 (1,4)
2.	010	10- (3,4)
3.	100
4.	101

	001	010	100	101
-01	v			v
10-			v	v

F = (-01) v (10-) v (010)

НЕ х2 /\ х3 \/ x1 /\ HE x2 \/ HE x1 /\ x2 /\ HE x3

Отчет по заданию 5

Вариант 24

Задание 1



Следующее высказывания записать в виде формул логики предикатов: студенты, которые пишут конспекты, не пишут шпаргалки.

Ɐх(S(x) /\ Ɐy ((K(y) => R(x, y)) /\ (H(y) => HE R(x, y)))

Задание 2

Построить таблицы истинности на области интерпретации D = {1,2}.

x(y(P(x) (RQ(y))))

Предикаты P(x), Q(y) на области интерпретации D = {1,2} принимают следующие значения:



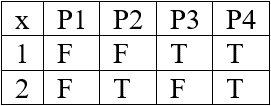
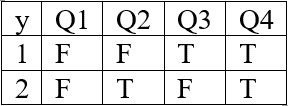
R – замкнутая формула, т.е. высказывание, которое принимает значение T и F.

---

Поскольку предикат P(x) принимает 4 значения, предикат Q(y) – 4 значения, формула R-2 значения, и в формуле Е нет свободных переменных, ее таблица истинности будет состоять из 4*4*2=32 строк.

y	R	R<=>Q(1)	R<=>Q(2)
q1	0	1	1
q1	1	0	0
q2	0	1	0
q2	1	0	1
q3	0	0	1
q3	1	1	0
q4	0	0	0
q4	1	1	1

---

				Ɐy					Ɐy	Ǝx
P1(1)Q1(1)R(0)	1	P1(1)Q1(2)R(0)	1	И	P1(2)Q1(1)R(0)	1	P1(2)Q1(2)R(0)	1	И	И
P1(1)Q1(1)R(1)	1	P1(1)Q1(2)R(1)	1	И	P1(2)Q1(1)R(1)	1	P1(2)Q1(2)R(1)	1	И	И
P1(1)Q2(1)R(0)	1	P1(1)Q2(2)R(0)	1	И	P1(2)Q2(1)R(0)	1	P1(2)Q2(2)R(0)	1	И	И
P1(1)Q2(1)R(1)	1	P1(1)Q2(2)R(1)	1	И	P1(2)Q2(1)R(1)	1	P1(2)Q2(2)R(1)	1	И	И
P1(1)Q3(1)R(0)	1	P1(1)Q3(2)R(0)	1	И	P1(2)Q3(1)R(0)	1	P1(2)Q3(2)R(0)	1	И	И
P1(1)Q3(1)R(1)	1	P1(1)Q3(2)R(1)	1	И	P1(2)Q3(1)R(1)	1	P1(2)Q3(2)R(1)	1	И	И
P1(1)Q4(1)R(0)	1	P1(1)Q4(2)R(0)	1	И	P1(2)Q4(1)R(0)	1	P1(2)Q4(2)R(0)	1	И	И
P1(1)Q4(1)R(1)	1	P1(1)Q4(2)R(1)	1	И	P1(2)Q4(1)R(1)	1	P1(2)Q4(2)R(1)	1	И	И
P2(1)Q1(1)R(0)	1	P2(1)Q1(2)R(0)	1	И	P2(2)Q1(1)R(0)	1	P2(2)Q1(2)R(0)	1	И	И
P2(1)Q1(1)R(1)	1	P2(1)Q1(2)R(1)	1	И	P2(2)Q1(1)R(1)	0	P2(2)Q1(2)R(1)	0	И	И
P2(1)Q2(1)R(0)	1	P2(1)Q2(2)R(0)	1	И	P2(2)Q2(1)R(0)	1	P2(2)Q2(2)R(0)	0	И	И
P2(1)Q2(1)R(1)	1	P2(1)Q2(2)R(1)	1	И	P2(2)Q2(1)R(1)	0	P2(2)Q2(2)R(1)	1	И	И
P2(1)Q3(1)R(0)	1	P2(1)Q3(2)R(0)	1	И	P2(2)Q3(1)R(0)	0	P2(2)Q3(2)R(0)	1	И	И
P2(1)Q3(1)R(1)	1	P2(1)Q3(2)R(1)	1	И	P2(2)Q3(1)R(1)	1	P2(2)Q3(2)R(1)	0	И	И
P2(1)Q4(1)R(0)	1	P2(1)Q4(2)R(0)	1	И	P2(2)Q4(1)R(0)	0	P2(2)Q4(2)R(0)	0	И	И
P2(1)Q4(1)R(1)	1	P2(1)Q4(2)R(1)	1	И	P2(2)Q4(1)R(1)	1	P2(2)Q4(2)R(1)	1	И	И
P3(1)Q1(1)R(0)	1	P3(1)Q1(2)R(0)	1	И	P3(2)Q1(1)R(0)	1	P3(2)Q1(2)R(0)	1	И	И
P3(1)Q1(1)R(1)	0	P3(1)Q1(2)R(1)	0	Л	P3(2)Q1(1)R(1)	1	P3(2)Q1(2)R(1)	1	И	И
P3(1)Q2(1)R(0)	1	P3(1)Q2(2)R(0)	0	Л	P3(2)Q2(1)R(0)	1	P3(2)Q2(2)R(0)	1	И	И
P3(1)Q2(1)R(1)	0	P3(1)Q2(2)R(1)	1	Л	P3(2)Q2(1)R(1)	1	P3(2)Q2(2)R(1)	1	И	И
P3(1)Q3(1)R(0)	0	P3(1)Q3(2)R(0)	1	Л	P3(2)Q3(1)R(0)	1	P3(2)Q3(2)R(0)	1	И	И
P3(1)Q3(1)R(1)	1	P3(1)Q3(2)R(1)	0	Л	P3(2)Q3(1)R(1)	1	P3(2)Q3(2)R(1)	1	И	И
P3(1)Q4(1)R(0)	0	P3(1)Q4(2)R(0)	0	Л	P3(2)Q4(1)R(0)	1	P3(2)Q4(2)R(0)	1	И	И
P3(1)Q4(1)R(1)	1	P3(1)Q4(2)R(1)	1	И	P3(2)Q4(1)R(1)	1	P3(2)Q4(2)R(1)	1	И	И
P4(1)Q1(1)R(0)	1	P4(1)Q1(2)R(0)	1	И	P4(2)Q1(1)R(0)	1	P4(2)Q1(2)R(0)	1	И	И
P4(1)Q1(1)R(1)	0	P4(1)Q1(2)R(1)	0	Л	P4(2)Q1(1)R(1)	0	P4(2)Q1(2)R(1)	0	Л	Л
P4(1)Q2(1)R(0)	1	P4(1)Q2(2)R(0)	0	Л	P4(2)Q2(1)R(0)	1	P4(2)Q2(2)R(0)	0	Л	Л
P4(1)Q2(1)R(1)	0	P4(1)Q2(2)R(1)	0	Л	P4(2)Q2(1)R(1)	0	P4(2)Q2(2)R(1)	1	Л	Л
P4(1)Q3(1)R(0)	0	P4(1)Q3(2)R(0)	1	Л	P4(2)Q3(1)R(0)	0	P4(2)Q3(2)R(0)	1	Л	Л
P4(1)Q3(1)R(1)	1	P4(1)Q3(2)R(1)	1	И	P4(2)Q3(1)R(1)	1	P4(2)Q3(2)R(1)	0	Л	Л
P4(1)Q4(1)R(0)	0	P4(1)Q4(2)R(0)	0	Л	P4(2)Q4(1)R(0)	0	P4(2)Q4(2)R(0)	0	Л	Л
P4(1)Q4(1)R(1)	1	P4(1)Q4(2)R(1)	0	Л	P4(2)Q4(1)R(1)	1	P4(2)Q4(2)R(1)	1	И	Л

---

---