Добавлен: 05.12.2023
Просмотров: 170
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задание 1
Для следующих формул найти СДНФ и СКНФ, каждую двумя способами (путем равносильных преобразований и используя таблицы истинности):
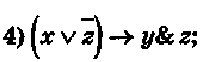
(Х \/ НЕ Z) => Y /\ Z
1.1 Найдём СДНФ и СКНФ, используя таблицы истинности
| Y | Z | Х | ¬Z | Х∨¬Z | Y∧Z | Х∨¬Z→Y∧Z | ЭК | ЭД |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | | Y∨Z∨X |
| 0 | 0 | 1 | 1 | 1 | 0 | 0 | | Y∨Z∨¬X |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | ¬Y∧Z∧¬X | |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 | | Y∨¬Z∨¬X |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | | ¬Y∨Z∨X |
| 1 | 0 | 1 | 1 | 1 | 0 | 0 | | ¬Y∨Z∨¬X |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | Y∧Z∧¬X | |
| 1 | 1 | 1 | 0 | 1 | 1 | 1 | Y∧Z∧X | |
СДНФ - ¬Y∧Z∧¬X \/ Y∧Z∧¬X \/ Y∧Z∧X
СКНФ - (Y∨Z∨Х) ∧ (Y∨Z∨¬Х) ∧ (Y∨¬Z∨¬Х) ∧ (¬Y∨Z∨Х) ∧ (¬Y∨Z∨¬Х)
1.2 Найдём СДНФ и СКНФ путем равносильных преобразований
ДНФ А = (Х \/ НЕ Z) => Y /\ Z = ¬X /\ Z \/ Y /\ Z = (¬X \/ Y) /\ Z = ¬X /\ Z \/ Y /\ Z
СДНФ А = ¬ X /\ Z /\ (Y \/ ¬Y) \/ Y /\ Z /\ (Х \/ ¬Х) = Y/\Z/\¬X \/ ¬Y/\ Z/\¬ X \/ Y /\ Z /\ X \/
\/ Y /\ Z /\ ¬X = ¬Y∧Z∧¬X \/ Y∧Z∧¬X \/ Y∧Z∧X
КНФ А = (¬X \/ Y) /\ Z
СКНФ А = (¬X \/ Y \/ (Z /\ ¬Z)) /\ (Z \/ (Х /\ ¬Х) \/ (Y /\ ¬Y) ) = (Y \/ Z \/ ¬X) /\
/\ (Y \/ ¬Z \/ ¬X) /\ (Y \/ Z \/ X) /\ (¬Y \/ Z \/ X) /\ (Y \/ Z \/ ¬Х) /\ (¬Y \/ Z \/ ¬Х) =
= (Y∨Z∨Х) ∧ (Y∨Z∨¬Х) ∧ (Y∨¬Z∨¬Х) ∧ (¬Y∨Z∨Х) ∧ (¬Y∨Z∨¬Х)
Задание 2
Найдите СДНФ для всякой тождественно истинной формулы,
содержащей: 1) одно переменное
| Х | F(x) | ЭК |
| 0 | 1 | ¬Х |
| 1 | 1 | Х |
СДНФ - ¬Х \/ Х
Задание 3
Найдите СКНФ для всякой тождественно ложной формулы, со-
держащей: 1) одно переменное
| Х | F(x) | ЭД |
| 0 | 0 | Х |
| 1 | 0 | ¬Х |
СКНФ - Х ∧ ¬Х
Задание 4
Докажите равносильность формул сравнением их совершенных нормальных форм (конъюнктивных или дизъюнктивных).
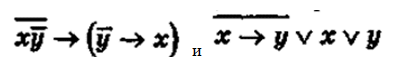
НЕ (Х ∧ НЕ Y) => (HE Y => X) = X ∧ HE Y \/ Y \/ X = X ∧ (HE Y \/ 1) \/ y = X \/ Y
НЕ (X => Y) \/ X \/ Y = HE(HE X \/ Y) \/ X \/ Y = HE X ∧ Y \/ X \/ Y =
= Y ∧ (HE X \/ 1) \/ X = Y \/ X
| X | Y | X \/ Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
| Y | X | Y \/ X |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
СДНФ (X \/ Y) – HE X ∧ Y \/ X ∧ HE Y \/ X ∧ Y
СДНФ (Y \/ X) - HE Y ∧ X \/ Y ∧ HE X \/ Y ∧ X
СДНФ (X \/ Y) = СДНФ (Y \/ X)
Задание 5
Найдите более простой вид формул, имеющих следующие со-
вершенные нормальные формы
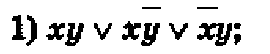
XY \/ X НЕ Y \/ HE XY = X ∧ (Y \/ HE Y) \/ HE X ∧ Y = X \/ HE X ∧ Y =
= (X \/ HE X) ∧ (X \/ Y) = X \/ Y
Ответ: X\/Y
Задание 6
Используя критерий тождественной истинности и тождествен-
ной ложности формулы, установить будет ли данная формула
тождественно истинной, тождественно ложной или выполни-
мой:
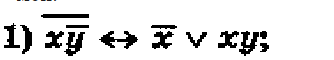
НЕ (X ∧ HE Y) HE X \/ X ∧ Y
НЕ X \/ Y (HE X \/ X) ∧ ( HE X \/ Y)
НЕ X \/ Y HE X \/ Y = 1
Ответ: формула тождественно истинна
Отчет по заданию 3
Задание 1
Доказать тождественную истинность
P ∧ Q => P
HE P \/ HE Q \/ P = HE Q \/ 1 = 1
Задание 2.
Доказать следующие правила вывода.
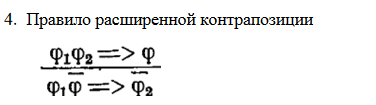
(A и B => C) => (А и НЕ С => НЕ B)
Задание 3.
Приёмы преобразования формул. Доказать тождественную истинность.
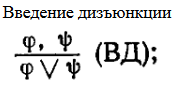
A |- A ∨ B, B |- A ∨ B
Применим Modus Ponens к формуле А и применим аксиому 6
A, B |- A → A ∨ B
А, А → А V В
Применим Modus Ponens
А V В
Задание 4
Доказать теорему дедукции на примере n =5
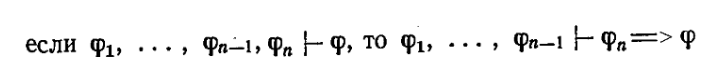







Задание 5.
Доказать правильность или неправильность рассуждений

p – многоугольник правильный
q – можно вписать окружность
(p => q) /\ (HE p => HE q)
| p | q | HE p | HE q | p => q | HE p => HE Q | (p => q) /\( HE p => HE q ) |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 |
Рассуждение неверно, так как из посылок p => q и НЕ р, не следует заключение НЕ q.
Отчет по заданию 4
Вариант 24
Записать функцию f(x1, x2, x3) и минимизировать её графическим методом, методом Карно, Квайна, Мак-Класки.
| Х1 | Х2 | Х3 | F(x1,x2,x3) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
F = HE x1 /\ HE x2 /\ x3 \/ НЕ х1 /\ х2 /\ НЕ х3 \/ х1 /\ НЕ х2 /\ НЕ 3 \/ х1 /\ НЕ х2 /\ х3
Графический метод
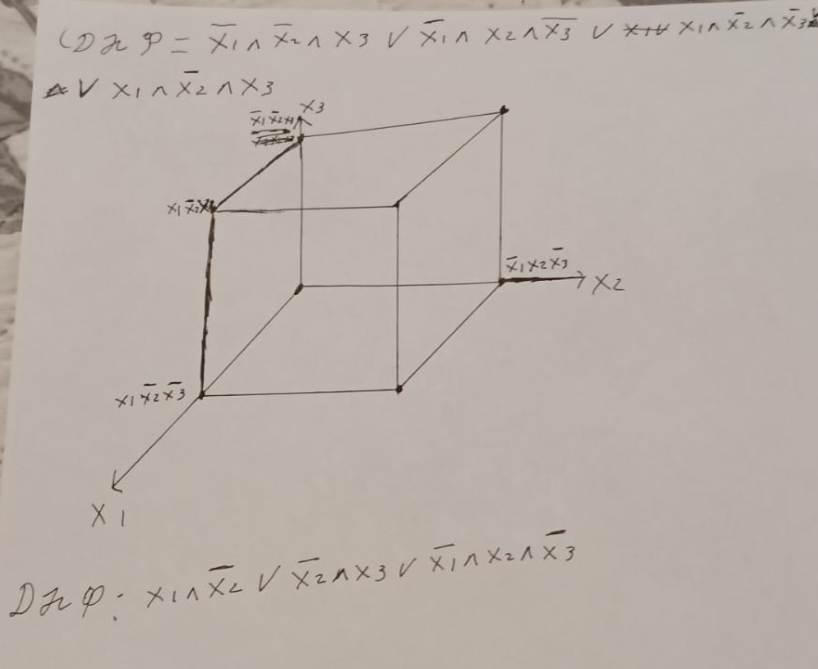
Метод Карно
F = HE x1 /\ HE x2 /\ x3 \/ НЕ х1 /\ х2 /\ НЕ х3 \/ х1 /\ НЕ х2 /\ НЕ 3 \/ х1 /\ НЕ х2 /\ х3
| | | х1 /\ НЕ х2 /\ х3 | х1 /\ НЕ х2 /\ НЕ 3 |
| НЕ х1 /\ х2 /\ НЕ х3 | | HE x1 /\ HE x2 /\ x3 | |

ДНФ – x1 /\ HE x2 \/ НЕ х2 /\ х3 \/ HE x1 /\ x2 /\ HE x3
Метод Квайна
| | Члены f(x1, x2, x3) | Результаты 1-го склеивания | Результаты 2-го склеивания |
| 1. | HE x1 /\ HE x2 /\ x3 | НЕ х2 /\ х3 (1,5) | |
| 2. | НЕ х1 /\ х2 /\ НЕ х3 | x1 /\ HE x2 (4,5) | |
| 3. | х1 /\ НЕ х2 /\ НЕ х3 | | |
| 4. | х1 /\ НЕ х2 /\ х3 | | |