ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 49
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1-дәрістік сабақ
Механика
Механика – қозғалыстың ең қарапайым түрлерінің заңдылықтарын, дене қозғалысының кеңістікте уақыт өтіуіне байланысты немесе олардың бөліктерінің бір-біріне қатысты орын ауыстыруын зерттейді Механика зерттелетін қозғалыстың сипатына қарай: кинематика, динамика және статика болып үш түрге бөлінеді.
1.1. Кинематика -қозғалысты тудыратын немесе оны өзгертетін себептерге тәуелсіз қозғалыс заңдылықтарын қарастыратын механиканың бөлімі. Теориялық зерттеулер кезінде практикалық есептерді жеңілдететін физикалық модельдер пайдаланылады. Осындай модельдің бірі ретінде берілген есепте өлшемін және пішінін есепке алынбайтын дене – материялық нүкте болып табылады. Мысалы, Күннің айналасында планеталардың қозғалыс заңдылықтарын зерттеу барысында оларды материялық нүкте деп қарастыруға болады.
Материялық нүкте қозғалысының кинематикалық сипаттамалары
Таңдап алынған санақ жүйесінде уақытқа тәуелді қозғалатын А материялық нүктенің күйі үш координатпен
Осы теңдеулерден уақытты шығарып, материялық нүкте қозғалыс траекториясының теңдеуін аламыз. Траектория деп нүктенің кеңістікте жүріп өткен сызығы (геометриялық нүктелер жиыны) айтылады. Траекторияның пішініне байланысты қозғалыс түзу сызықты және қисық сызықты (шеңбер бойымен, парабола бойынша, кез келген қисық сызық бойынша қозғалыс) болып бөлінеді. Материялық нүкте қозғалысының (1.1.)-теңдеудегі үш түрлі скалярлық теңдеулерді бір ғана векторлық теңдеумен алмастыруға болады;
мұндағы

1.1-сурет 1.2-сурет
1.2. Жылдамдық және үдеу
Қозғалыстың кинематикалық сипаттамалары векторлық шамалар
Лездік жылдамдық ұғымын енгізейік. Егер
Жылдамдық шамасы жол теңдеуінің бірінші туындысы арқылы да анықталады.
(1.4) өрнегінен
Бұл материалық нүктенің өте аз dt уақыт ішінде жүрген шексіз аз жолы. Берілген t yақыт ішінде жүрілген жол (1.5.) өрнегін интегралдау арқылы анықталады
Халықаралық бірліктер жүйесінде (ХБЖ) жылдамдықтың өлшем бірлігі
Бірқалыпты емес қозғалыс кезінде нүкте жылдамдығы шама және бағыты жағынан уақытқа тәуелді өзгереді. Жылдамдықтың шама бойынша және бағыты бойынша өзгеруін сипаттайтын шаманы үдеу деп атайды. Орташа үдеудің шамасы
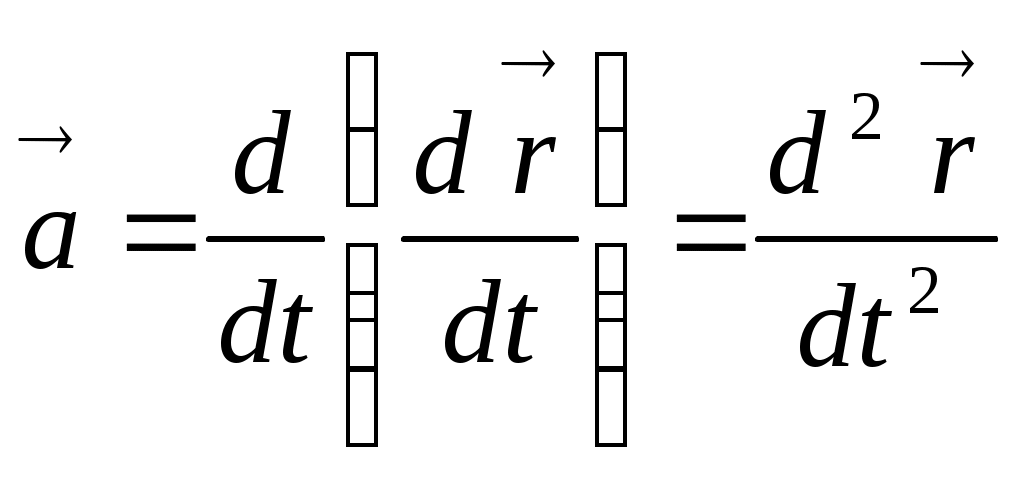 (1.8)
(1.8) 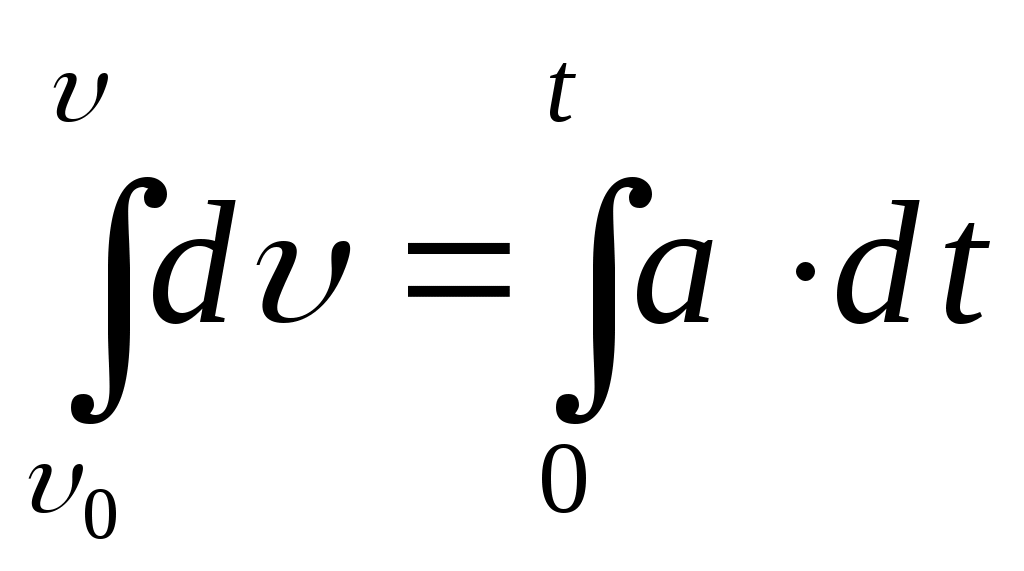 ,
, Мұндағы
(1.9) теңдеуінен бірқалыпты айнымалы қозғалыс кезінде жылдамдық уақыт бойынша сызықтық түрде өзгеретіндігі көрінеді. Жылдамдықтың мәнін (1.6) теңдеуге қойып жолды табамыз
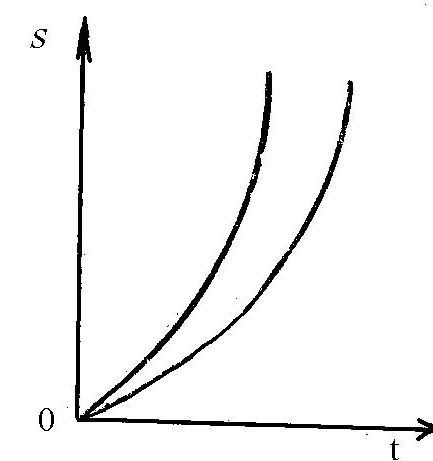
1.3-сурет
Бірқалыпты айнымалы қозғалыс кезіндегі нүктенің өткен жолы
уақыттың функциясы болып табылады. Оның графигінің түрі үдеудің модулі мен таңбасына байланысты (1.3–сурет) парабола болып табылады.
1.3. Қисық сызықты қозғалыс кезіндегі жылдамдық және үдеу
Қозғалған нүктенің толық үдеуі
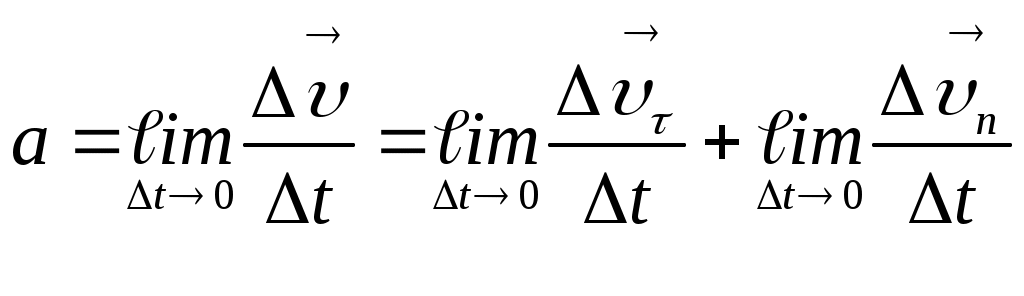 . (1.11)
. (1.11)
Үдеудің бірінші құраушысы:
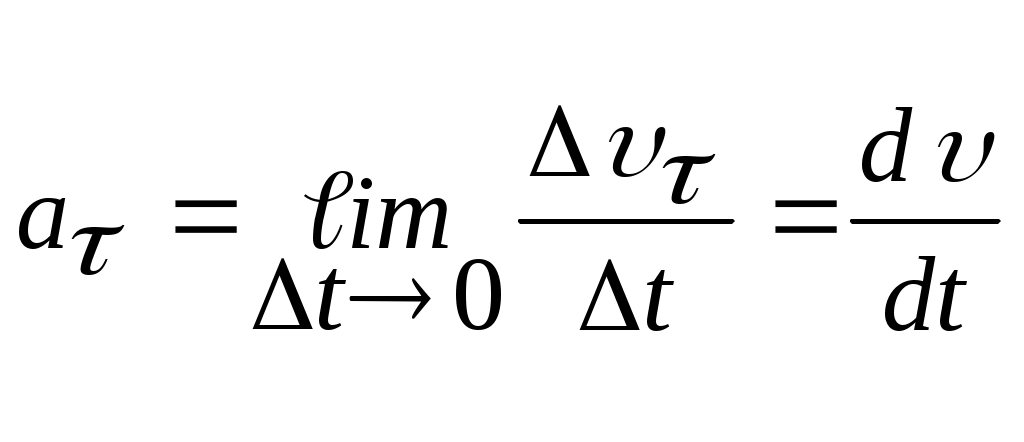 . (1.12)
. (1.12)
Бұл жанама немесе тангенциал үдеу деп аталады, ол жылдамдық модулінен уақыт бойынша алынған бірінші туындысына тең және жылдамдықтың сан мәнінің уақыт бойынша өзгеруін сипаттайды. Үдеудің екінші 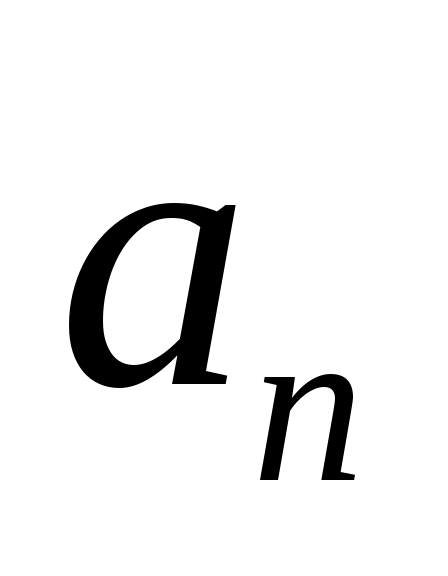 құраушысы:
құраушысы: 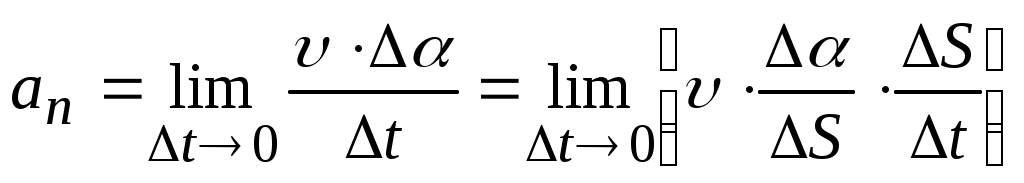
мұндағы 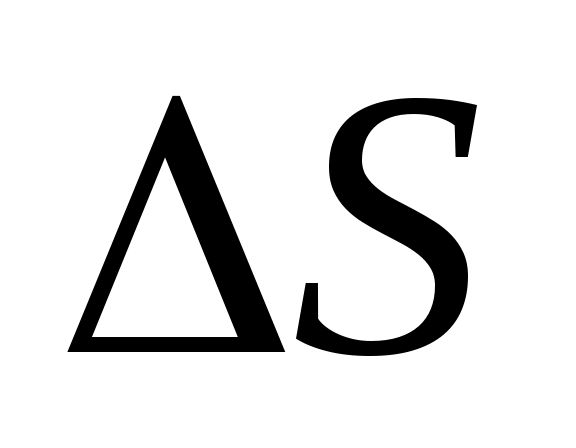 -АВ доғасының ұзындығы.
-АВ доғасының ұзындығы. 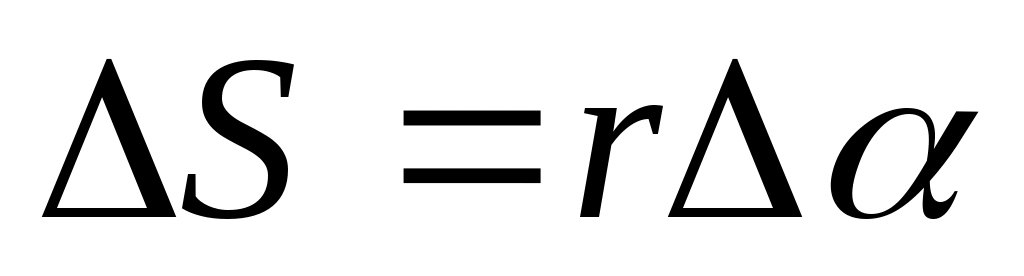 болғандықтан, мұндағы
болғандықтан, мұндағы 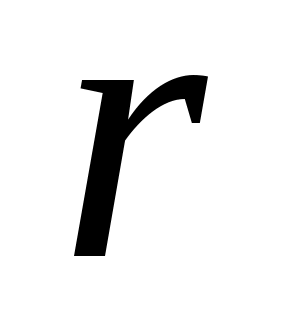 -А нүктесіндегі траекторияның қисықтық радиусы. Олай болса,
-А нүктесіндегі траекторияның қисықтық радиусы. Олай болса, 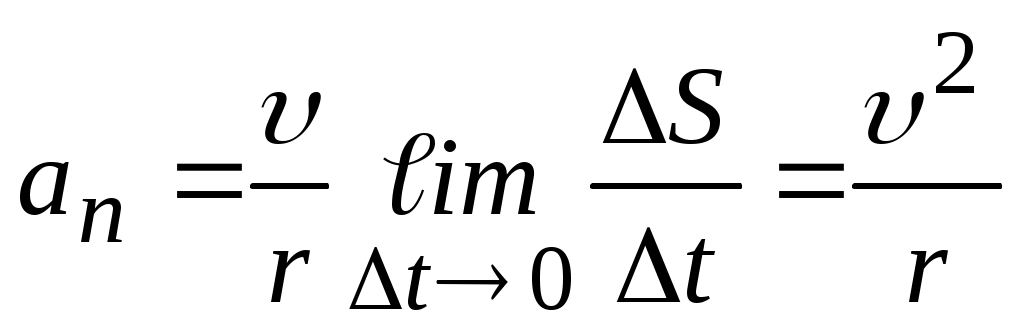 . (1.13)
. (1.13)
(1.11) теңдеуге сәйкес материалдық нүктенің толық үдеуі нормаль және тангенциалды үдеулердің векторлық қосындысына тең, яғни 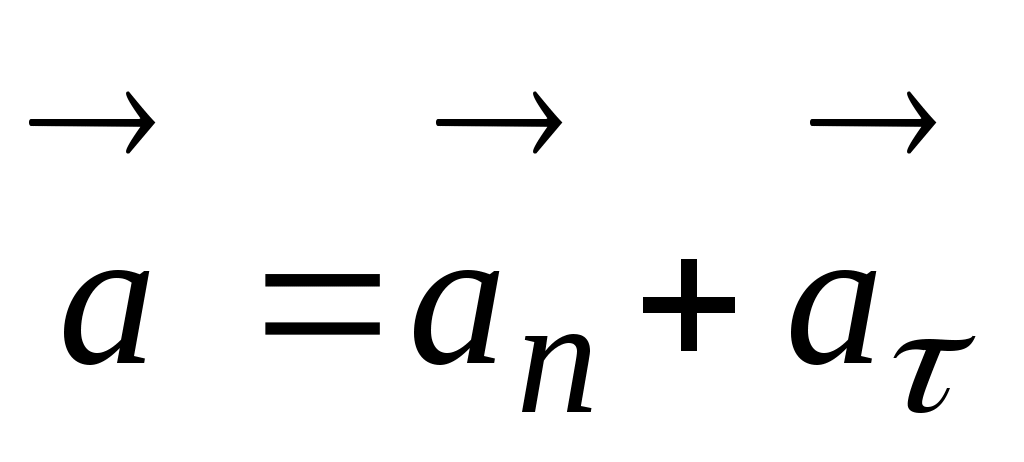 .
.
Толық үдеудің модулі: 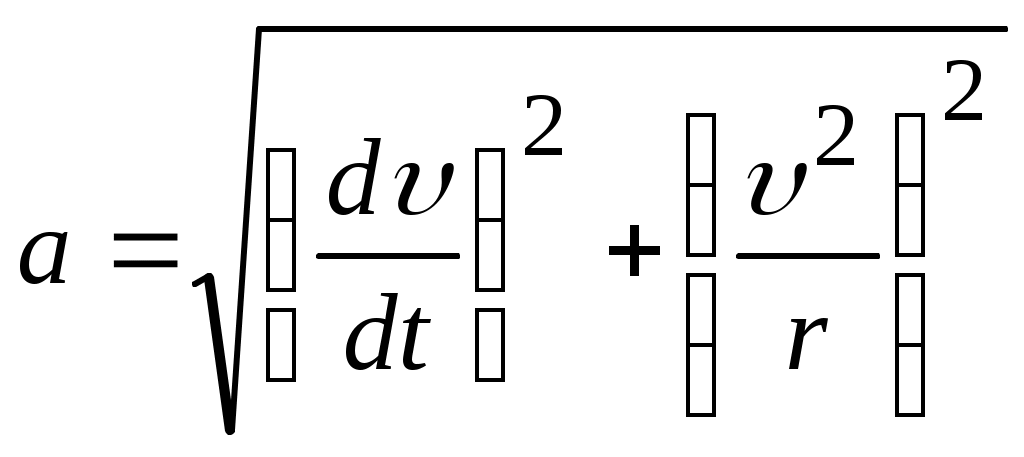 . (1.14)
. (1.14)
1.4. Айналмалы қозғалыс кинематикасы.
Бұрыштық жылдамдық және бұрыштық үдеу
Дененің айналу бұрышының уақыт бойынша бірінші туындысына тең векторлық шама бұрыштық жылдамдық деп аталады, яғни:
Егер
Толық бір айналуға
немесе
Мұндағы
Дененің бірқалыпты емес айналу кезінде бұрыштық жылдамдықтың өзгеруін бұрыштық үдеу арқылы сипаттауға болады. Егер шексіз аз
