ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 62
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
және 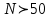 жыл ұқсас өзендер үшін жылдық ағындының интегралдық айырым қисығын тұрғызып талдау арқылы жүзеге асырылады. Қысқа
жыл ұқсас өзендер үшін жылдық ағындының интегралдық айырым қисығын тұрғызып талдау арқылы жүзеге асырылады. Қысқа  жылдан тұратын қатарбойынша есептелгенстатистикалық өлшемдік көрсеткіштерінің
жылдан тұратын қатарбойынша есептелгенстатистикалық өлшемдік көрсеткіштерінің 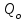 ,
, 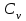 және
және 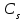 репрезентативтілігі ұқсас тұстаманың деректері бойынша
репрезентативтілігі ұқсас тұстаманың деректері бойынша  және
және 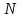 кезеңдері үшін тұрғызылған жылдық ағындыны қамтамасыздық қисықтарын салыстыру арқылы анықтайды[17;18; 19; 20].
кезеңдері үшін тұрғызылған жылдық ағындыны қамтамасыздық қисықтарын салыстыру арқылы анықтайды[17;18; 19; 20].
Гидрометриялық бағалауақпараттық деректер жеткілікті болған жағдайда қалыпты жылдық ағынды анықтау үшін статистикалық қатардың кез келген арифметикалық орташа шамасы ретінде келесі өрнекті пайдалануға болады[10;11; 12; 13 ]:
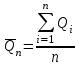 , (3.1)
, (3.1)
мұнда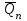 - қалыпты жылдық ағынды, м/с;
- қалыпты жылдық ағынды, м/с; 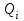 - қатардағы жылдар санының көбеюімен нің орташа арифметикалық шамасы өзгермейтін немесе аз өзгеретін ұзақ кезең ішіндегі ағындының жылдық мәндері.
- қатардағы жылдар санының көбеюімен нің орташа арифметикалық шамасы өзгермейтін немесе аз өзгеретін ұзақ кезең ішіндегі ағындының жылдық мәндері.
Қателіктер теориясына сәйкес бағалау қатарының саны жеткілікті дәрежеде үлкен болғанда салыстырмалы қысқа таңдама бойынша анықталған орташа арифметикалық мәнімен бас жиынтық орташасының немесе математикалық күтім арасындағы айырым барынша мардымсыз болады, яғни жылдықорташа квадраттық қателігі таңдамасының ұлғаюымен аталады және мына өрнек бойынша анықталады[17;18; 19; 20]:
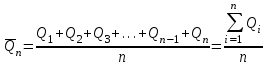 , (3.2)
, (3.2)
мұнда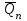 - жылдық ағындының бірлік мәндері, м3/с;
- жылдық ағындының бірлік мәндері, м3/с; 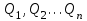 - қатардағы жылдар санының көбеюімен
- қатардағы жылдар санының көбеюімен 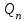 -ның орташа арифметикалық шамасы өзгермейтін немесе өзгеретін
-ның орташа арифметикалық шамасы өзгермейтін немесе өзгеретін 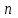 ұзақ кезең ішіндегі ағындының жылдық мәндері.
ұзақ кезең ішіндегі ағындының жылдық мәндері.
Қателіктер теориясына сәйкес:
 (бағалау қатарының саны) жеткілікті дәрежеде үлкен болғанда салыстырмалы қысқа таңдама бойынша анықталған орташа арифметикалық мәнмен
(бағалау қатарының саны) жеткілікті дәрежеде үлкен болғанда салыстырмалы қысқа таңдама бойынша анықталған орташа арифметикалық мәнмен  бас жиынтық
бас жиынтық  орташасының немесе математикалық күтім арасындағы айырым барынша мардымсыз болады, яғни
орташасының немесе математикалық күтім арасындағы айырым барынша мардымсыз болады, яғни  – жылдық орташаның орташа квадраттық қателігі
– жылдық орташаның орташа квадраттық қателігі  таңдамасының ұлғаюымен аталды және келесі өрнекпен өрнектеледі[17;18; 19; 20]:
таңдамасының ұлғаюымен аталды және келесі өрнекпен өрнектеледі[17;18; 19; 20]:
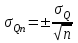 , (3.3)
, (3.3)
мұнда – жылдық ағындының бірлік мәндерінің, ағындының жылдық орташа мәнінен орташа квадраттық ауытқуы және ол келесі өрнек бойынша анықталады[10; 11; 12; 13]:
– жылдық ағындының бірлік мәндерінің, ағындының жылдық орташа мәнінен орташа квадраттық ауытқуы және ол келесі өрнек бойынша анықталады[10; 11; 12; 13]:
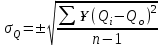 . (3.4)
. (3.4)
Сонымен, стандарт қателік көмегімен есептелген шамалардың немесе таңдаманың орташа мәнінің сенімділігі бағаланады.
Өзеннің ағындысын зерттеу немесе есептеу тәжірибесінде салыстырмалы орташа квадраттық қателік жиі қолданылады. Оның мәні сулылығы әртүрлі өзендердің қалыпты ағындысын анықтаудың дәлділігін салыстыру үшін пайдаланылады. Сонымен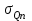 ді
ді  дің пайызы есебімен өрнектеп, шектелген
дің пайызы есебімен өрнектеп, шектелген  жыл қатары бойынша есептелген қалыпты ағындының салыстырмалы орташа квадраттық қателігін аламыз[17;18; 19; 20]:
жыл қатары бойынша есептелген қалыпты ағындының салыстырмалы орташа квадраттық қателігін аламыз[17;18; 19; 20]:
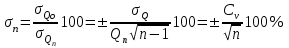 , (3.5)
, (3.5)
мұнда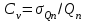 ағындының уақыт бойынша құбылмалылығын көрсетеді және вариация көрсеткішімен немесе өзгергіштік көрсеткішімен сипатталады. Вариация көрсеткіші ағындының жылдық мәндерінің өздерінің орташа мәніне қатысты тербелуін көрсетеді және тікелей қолдағы Бағалау қатары бойынша анықталады.
ағындының уақыт бойынша құбылмалылығын көрсетеді және вариация көрсеткішімен немесе өзгергіштік көрсеткішімен сипатталады. Вариация көрсеткіші ағындының жылдық мәндерінің өздерінің орташа мәніне қатысты тербелуін көрсетеді және тікелей қолдағы Бағалау қатары бойынша анықталады.
Вариация көрсеткішінің мәні неғұрлым үлкен болған сайын, ділдігі берілген қалыпты ағындыны анықтауға қажетті бағалау қатарының ұзақтығы соғұрлым ұзағырақ болуы керек[10;11; 12; 13].
мәні неғұрлым үлкен болған сайын, ділдігі берілген қалыпты ағындыны анықтауға қажетті бағалау қатарының ұзақтығы соғұрлым ұзағырақ болуы керек[10;11; 12; 13].
3.2 Нұра өзені су ағынының гидрологиялық сипаттамаларын есептеу
Бағалау қатарындағы жылдар саны жылдан аспайтын жағдайлардың барлығында есептік репрезентативті кезең белгіленеді. Ол суы мол және суы аз жылдар тобынан тұратын аяқталған айналымдардың ең көп санынан тұрады. Тек үлкен аумаққа таралатын және осы ауданның барлық өзендерін қамтитын негізгі ұзақ айналымдар ғана назарға алынады. Негізгі айналымдарға қабаттасқан ұзақтығы кішкентай айналымдар есепке алынбайды. Тек қана су мол немесе суы аз кезеңдерден тұратын толық емес айналымдар шығарылып тасталады.
Айырымдық интеграл қисықтары жекеленген салыстырмалы қысқа кезеңдері ағындысының тербелісін есепке алады. Ол модулдік көрсеткішінің орташа мәнінен ауытқуын қосу жолымен тұрғызылады, яғни оның қатынасы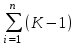 ретінде тұрғызылады. Мұндағы
ретінде тұрғызылады. Мұндағы 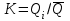 модулдік көрсеткіш. Сонымен қисықтың ординатасы әрбір жылдың соңында модулдік көрсеткіштің қалыпты шамадан немесе көпжылдық орташамәнінен
модулдік көрсеткіш. Сонымен қисықтың ординатасы әрбір жылдың соңында модулдік көрсеткіштің қалыпты шамадан немесе көпжылдық орташамәнінен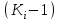 ауытқуының қосындысын өсу ретімен береді (кесте 3.1 ) [1; 15; 16; 21; 23].
ауытқуының қосындысын өсу ретімен береді (кесте 3.1 ) [1; 15; 16; 21; 23].
Кесте 3.1
Нұра өзеніСергиопольскоебекеті бойынша қалпына келтірілген ұзын қатардың вариация коэффициентін анықтау
3.1 кестенің жалғасы
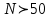 жыл ұқсас өзендер үшін жылдық ағындының интегралдық айырым қисығын тұрғызып талдау арқылы жүзеге асырылады. Қысқа
жыл ұқсас өзендер үшін жылдық ағындының интегралдық айырым қисығын тұрғызып талдау арқылы жүзеге асырылады. Қысқа  жылдан тұратын қатарбойынша есептелгенстатистикалық өлшемдік көрсеткіштерінің
жылдан тұратын қатарбойынша есептелгенстатистикалық өлшемдік көрсеткіштерінің 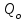 ,
, 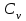 және
және 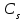 репрезентативтілігі ұқсас тұстаманың деректері бойынша
репрезентативтілігі ұқсас тұстаманың деректері бойынша  және
және 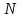 кезеңдері үшін тұрғызылған жылдық ағындыны қамтамасыздық қисықтарын салыстыру арқылы анықтайды[17;18; 19; 20].
кезеңдері үшін тұрғызылған жылдық ағындыны қамтамасыздық қисықтарын салыстыру арқылы анықтайды[17;18; 19; 20].Гидрометриялық бағалауақпараттық деректер жеткілікті болған жағдайда қалыпты жылдық ағынды анықтау үшін статистикалық қатардың кез келген арифметикалық орташа шамасы ретінде келесі өрнекті пайдалануға болады[10;11; 12; 13 ]:
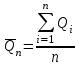 , (3.1)
, (3.1)мұнда
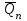 - қалыпты жылдық ағынды, м/с;
- қалыпты жылдық ағынды, м/с; 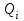 - қатардағы жылдар санының көбеюімен нің орташа арифметикалық шамасы өзгермейтін немесе аз өзгеретін ұзақ кезең ішіндегі ағындының жылдық мәндері.
- қатардағы жылдар санының көбеюімен нің орташа арифметикалық шамасы өзгермейтін немесе аз өзгеретін ұзақ кезең ішіндегі ағындының жылдық мәндері.Қателіктер теориясына сәйкес бағалау қатарының саны жеткілікті дәрежеде үлкен болғанда салыстырмалы қысқа таңдама бойынша анықталған орташа арифметикалық мәнімен бас жиынтық орташасының немесе математикалық күтім арасындағы айырым барынша мардымсыз болады, яғни жылдықорташа квадраттық қателігі таңдамасының ұлғаюымен аталады және мына өрнек бойынша анықталады[17;18; 19; 20]:
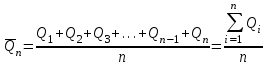 , (3.2)
, (3.2)мұнда
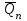 - жылдық ағындының бірлік мәндері, м3/с;
- жылдық ағындының бірлік мәндері, м3/с; 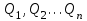 - қатардағы жылдар санының көбеюімен
- қатардағы жылдар санының көбеюімен 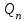 -ның орташа арифметикалық шамасы өзгермейтін немесе өзгеретін
-ның орташа арифметикалық шамасы өзгермейтін немесе өзгеретін 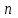 ұзақ кезең ішіндегі ағындының жылдық мәндері.
ұзақ кезең ішіндегі ағындының жылдық мәндері.Қателіктер теориясына сәйкес:
 (бағалау қатарының саны) жеткілікті дәрежеде үлкен болғанда салыстырмалы қысқа таңдама бойынша анықталған орташа арифметикалық мәнмен
(бағалау қатарының саны) жеткілікті дәрежеде үлкен болғанда салыстырмалы қысқа таңдама бойынша анықталған орташа арифметикалық мәнмен  бас жиынтық
бас жиынтық  орташасының немесе математикалық күтім арасындағы айырым барынша мардымсыз болады, яғни
орташасының немесе математикалық күтім арасындағы айырым барынша мардымсыз болады, яғни  – жылдық орташаның орташа квадраттық қателігі
– жылдық орташаның орташа квадраттық қателігі  таңдамасының ұлғаюымен аталды және келесі өрнекпен өрнектеледі[17;18; 19; 20]:
таңдамасының ұлғаюымен аталды және келесі өрнекпен өрнектеледі[17;18; 19; 20]: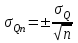 , (3.3)
, (3.3)мұнда
 – жылдық ағындының бірлік мәндерінің, ағындының жылдық орташа мәнінен орташа квадраттық ауытқуы және ол келесі өрнек бойынша анықталады[10; 11; 12; 13]:
– жылдық ағындының бірлік мәндерінің, ағындының жылдық орташа мәнінен орташа квадраттық ауытқуы және ол келесі өрнек бойынша анықталады[10; 11; 12; 13]: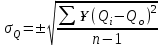 . (3.4)
. (3.4)Сонымен, стандарт қателік көмегімен есептелген шамалардың немесе таңдаманың орташа мәнінің сенімділігі бағаланады.
Өзеннің ағындысын зерттеу немесе есептеу тәжірибесінде салыстырмалы орташа квадраттық қателік жиі қолданылады. Оның мәні сулылығы әртүрлі өзендердің қалыпты ағындысын анықтаудың дәлділігін салыстыру үшін пайдаланылады. Сонымен
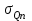 ді
ді  дің пайызы есебімен өрнектеп, шектелген
дің пайызы есебімен өрнектеп, шектелген  жыл қатары бойынша есептелген қалыпты ағындының салыстырмалы орташа квадраттық қателігін аламыз[17;18; 19; 20]:
жыл қатары бойынша есептелген қалыпты ағындының салыстырмалы орташа квадраттық қателігін аламыз[17;18; 19; 20]: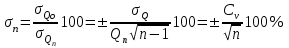 , (3.5)
, (3.5)мұнда
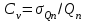 ағындының уақыт бойынша құбылмалылығын көрсетеді және вариация көрсеткішімен немесе өзгергіштік көрсеткішімен сипатталады. Вариация көрсеткіші ағындының жылдық мәндерінің өздерінің орташа мәніне қатысты тербелуін көрсетеді және тікелей қолдағы Бағалау қатары бойынша анықталады.
ағындының уақыт бойынша құбылмалылығын көрсетеді және вариация көрсеткішімен немесе өзгергіштік көрсеткішімен сипатталады. Вариация көрсеткіші ағындының жылдық мәндерінің өздерінің орташа мәніне қатысты тербелуін көрсетеді және тікелей қолдағы Бағалау қатары бойынша анықталады.Вариация көрсеткішінің
 мәні неғұрлым үлкен болған сайын, ділдігі берілген қалыпты ағындыны анықтауға қажетті бағалау қатарының ұзақтығы соғұрлым ұзағырақ болуы керек[10;11; 12; 13].
мәні неғұрлым үлкен болған сайын, ділдігі берілген қалыпты ағындыны анықтауға қажетті бағалау қатарының ұзақтығы соғұрлым ұзағырақ болуы керек[10;11; 12; 13].
3.2 Нұра өзені су ағынының гидрологиялық сипаттамаларын есептеу
Бағалау қатарындағы жылдар саны жылдан аспайтын жағдайлардың барлығында есептік репрезентативті кезең белгіленеді. Ол суы мол және суы аз жылдар тобынан тұратын аяқталған айналымдардың ең көп санынан тұрады. Тек үлкен аумаққа таралатын және осы ауданның барлық өзендерін қамтитын негізгі ұзақ айналымдар ғана назарға алынады. Негізгі айналымдарға қабаттасқан ұзақтығы кішкентай айналымдар есепке алынбайды. Тек қана су мол немесе суы аз кезеңдерден тұратын толық емес айналымдар шығарылып тасталады.
Айырымдық интеграл қисықтары жекеленген салыстырмалы қысқа кезеңдері ағындысының тербелісін есепке алады. Ол модулдік көрсеткішінің орташа мәнінен ауытқуын қосу жолымен тұрғызылады, яғни оның қатынасы
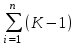 ретінде тұрғызылады. Мұндағы
ретінде тұрғызылады. Мұндағы 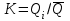 модулдік көрсеткіш. Сонымен қисықтың ординатасы әрбір жылдың соңында модулдік көрсеткіштің қалыпты шамадан немесе көпжылдық орташамәнінен
модулдік көрсеткіш. Сонымен қисықтың ординатасы әрбір жылдың соңында модулдік көрсеткіштің қалыпты шамадан немесе көпжылдық орташамәнінен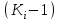 ауытқуының қосындысын өсу ретімен береді (кесте 3.1 ) [1; 15; 16; 21; 23].
ауытқуының қосындысын өсу ретімен береді (кесте 3.1 ) [1; 15; 16; 21; 23]. Кесте 3.1
Нұра өзеніСергиопольскоебекеті бойынша қалпына келтірілген ұзын қатардың вариация коэффициентін анықтау
| № | Жылдар |  , ,м3/с | 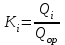 | 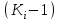 | 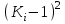 | 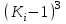 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 1934 | 4,22 | 0,581 | -0,419 | 0,176 | -0,073 |
| 2 | 1935 | 4,99 | 0,688 | -0,312 | 0,097 | -0,030 |
| 3 | 1936 | 0,36 | 0,050 | -0,950 | 0,903 | -0,857 |
| 4 | 1937 | 1,11 | 0,153 | -0,847 | 0,717 | -0,608 |
| 5 | 1938 | 0,81 | 0,112 | -0,888 | 0,788 | -0,700 |
| 6 | 1939 | 1,33 | 0,183 | -0,817 | 0,667 | -0,545 |
| 7 | 1940 | 1,95 | 0,269 | -0,731 | 0,534 | -0,390 |
| 8 | 1941 | 11,8 | 1,627 | 0,627 | 0,393 | 0,246 |
| 9 | 1942 | 4,14 | 0,570 | -0,430 | 0,185 | -0,079 |
| 10 | 1943 | 8,24 | 1,136 | 0,136 | 0,018 | 0,003 |
| 11 | 1944 | 5,42 | 0,747 | -0,253 | 0,064 | -0,016 |
| 12 | 1945 | 8,93 | 1,231 | 0,231 | 0,053 | 0,012 |
| 13 | 1946 | 2,21 | 0,305 | -0,695 | 0,483 | -0,336 |
| 14 | 1947 | 9,70 | 1,337 | 0,337 | 0,113 | 0,038 |
| 15 | 1948 | 23,0 | 3,171 | 2,171 | 4,713 | 10,232 |
| 16 | 1949 | 11,7 | 1,613 | 0,613 | 0,375 | 0,230 |
| 17 | 1950 | 7,02 | 0,968 | -0,032 | 0,001 | -0,001 |
| 18 | 1951 | 1,21 | 0,167 | -0,833 | 0,780 | -0,688 |
| 19 | 1952 | 5,37 | 0,740 | -0,260 | 0,068 | -0,017 |
| 20 | 1953 | 3,30 | 0,455 | -0,545 | 0,267 | -0,162 |
| 21 | 1954 | 16,0 | 2,206 | 1,206 | 1,454 | 1,754 |
| 22 | 1955 | 3,98 | 0,549 | -0,451 | 0,203 | -0,019 |
| 23 | 1956 | 1,11 | 0,153 | -0,847 | 0,717 | -0,607 |
| 24 | 1957 | 1,44 | 0,198 | -0,802 | 0,643 | -0,516 |
| 25 | 1958 | 8,12 | 1,120 | 0,120 | 0,014 | 0,001 |
| 26 | 1959 | 8,51 | 1,173 | 0,173 | 0,030 | 0,005 |
3.1 кестенің жалғасы
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 27 | 1960 | 14,6 | 2,013 | 1,013 | 1,026 | 1,039 |
| 28 | 1961 | 6,75 | 0,931 | -0,069 | 0,004 | -0,001 |
| 29 | 1962 | 8,04 | 1,108 | 0,108 | 0,011 | 0,001 |
| 30 | 1963 | 0,85 | 0,117 | -0,883 | 0,780 | -0,688 |
| 31 | 1964 | 3,68 | 0,507 | -0,493 | 0,243 | -0,119 |
| 32 | 1965 | 2,42 | 0,333 | -0,667 | 0,445 | -0,297 |
| 33 | 1966 | 9,81 | 1,352 | 0,152 | 0,023 | 0,003 |
| 34 | 1967 | 0,42 | 0,058 | -0,942 | 0,887 | -0,836 |
| 35 | 1968 | 1,54 | 0,212 | -0,788 | 0,621 | -0,489 |
| 36 | 1969 | 4,72 | 0,651 | -0,349 | 0,122 | -0,042 |
| 37 | 1970 | 4,34 | 0,598 | -0,402 | 0,161 | -0,065 |
| 38 | 1971 | 10,9 | 1,503 | 0,503 | 0,253 | 0,0016 |
| 39 | 1972 | 6,61 | 0,911 | -0,089 | 0,007 | -0,001 |
| 40 | 1973 | 7,64 | 1,053 | 0,053 | 0,003 | 0,001 |
| 41 | 1974 | 6,62 | 0,913 | -0,087 | 0,007 | -0,001 |
| 42 | 1975 | 9,05 | 1,248 | 0,248 | 0,061 | 0,015 |
| 43 | 1976 | 9,90 | 1,365 | 0,365 | 0,133 | 0,048 |
| 44 | 1977 | 17,4 | 2,399 | 1,399 | 1,957 | 2,738 |
| 45 | 1978 | 7,35 | 1,013 | 0,013 | 0,001 | 0,001 |
| 46 | 1979 | 10,4 | 1,434 | 0,434 | 0,188 | 0,082 |
| 47 | 1980 | 7,12 | 0,981 | -0,019 | 0,001 | -0,001 |
| 48 | 1981 | 6,69 | 0,922 | -0,078 | 0,006 | -0,001 |
| 49 | 1982 | 7,67 | 1,057 | 0,057 | 0,003 | -0,001 |
| 50 | 1983 | 9,71 | 1,338 | 0,338 | 0,114 | 0,039 |
| 51 | 1984 | 7,31 | 1,008 | 0,008 | 0,001 | 0,001 |
| 52 | 1985 | 9,92 | 1,368 | 0,368 | 0,135 | 0,050 |
| 53 | 1986 | 13,4 | 1,848 | 0,848 | 0,719 | 0,609 |
| 54 | 1987 | 7,87 | 1,085 | 0,085 | 0,007 | 0,001 |
| 55 | 1988 | 15,1 | 2,082 | 1,082 | 1,170 | 1,266 |
| 56 | 1989 | 8,83 | 1,217 | 0,217 | 0,047 | 0,010 |
| 57 | 1990 | 16,1 | 2,200 | 1,200 | 1,440 | 1,728 |
| 58 | 1991 | 14,5 | 1,200 | 0,200 | 0,040 | 0,008 |
| 59 | 1992 | 3,23 | 0,445 | -0,555 | 0,308 | -0,170 |
| 60 | 1993 | 19,9 | 2,743 | 1,743 | 3,038 | 5,295 |
| 61 | 1994 | 4,58 | 0,631 | -0,369 | 0,136 | -0,050 |
| 62 | 1995 | 12,9 | 1,779 | 0,779 | 0,606 | 0,473 |
| 63 | 1996 | 4,28 | 0,590 | -0,410 | 0,168 | -0,068 |
| 64 | 1997 | 6,57 | 0,906 | -0,094 | 0,088 | -0,001 |