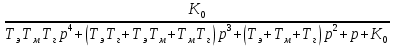.

Заданные параметры являются параметрами основных элементов, из которых состоит следящая система, используя эти параметры необходимо провести анализ динамики следящей системы и в случае невыполнения желаемых показателей качества провести синтез корректирующего звена, которое обеспечивает желаемые показатели качества следящей системы.

2. Математическая модель следящей системы

Математическая модель – математическое представление реальности, один из вариантов модели, как системы, исследование которой позволяет получать информацию о некоторой другой системе.

Процесс построения и изучения математических моделей называется математическим моделированием.

1. 
   Функциональная схема следящей системы
   

Функциональная схема – вид графической модели системы. Их использование и построение позволяет наглядно отразить функции выполняемые каждым устройством в системах автоматического управления. Для следящей системы функциональная схема приведена на рис 2:



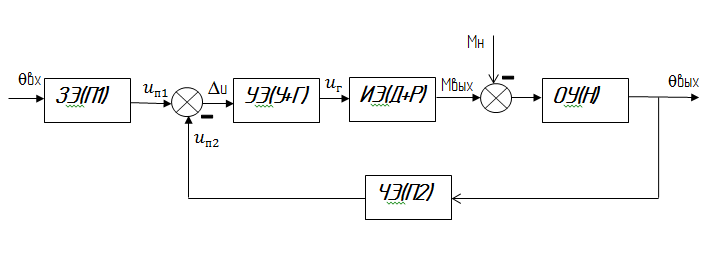
Рис.2 – Функциональная схема следящей системы

2. 
   Уравнения движения следящей системы
   

Составим математические модели каждого элемента согласно схеме, приведенной на рис. 2

а) Уравнения потенциометров:





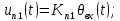
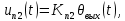
где = – напряжения на потенциометрах П1 и П2 соответственно; 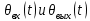– задающий и выходной углы поворота валов следящей системы; 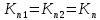– коэффициенты передачи потенциометров.

б) Уравнение элемента сравнения

---

.

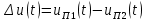При условии, что , имеем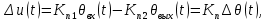



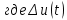– напряжение подаваемое на усилитель; 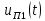и 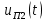- напряжения на П1 и П2 соответственно; 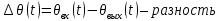входного и выходного углов поворота валов системы.

в) Уравнение усилителя имеет вид



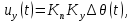
где 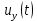– напряжение на усилителе;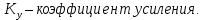

г) Уравнение генератора запишем в виде



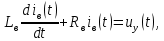
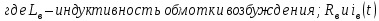– сопротивление и ток обмотки возбуждения;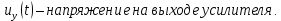

д) Уравнения электродвигателя:



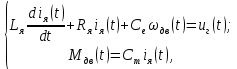
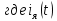– ток якоря электродвигателя, 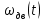– угловая скорость вращения вала двигателя, 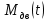– момент, развиваемый двигателем, 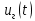– напряжение, вырабатываемое генератором, 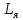и – индуктивность и сопротивление обмотки якоря.

е) Уравнение нагрузки имеет вид

= ,

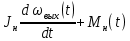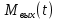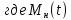– возмущающий момент на входном валу, – момент инерции нагрузки,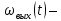

---

угловая скорость выходного вала,

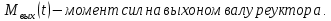
ж) Уравнения редуктора запишем в следующей упрощенной форме



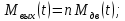
где n 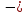передаточное число редуктора.

з) Уравнение связи между углом поворота и угловой скоростью имеет вид



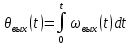
Таким образом, общаясистема уравнений следящей системы имеет следующий вид:

(1)

---

2.3 Передаточные функции элементов следящей системы

Система уравнений следящей системы в операторной форме выглядит следующим образом:

(2)

2.4 Структурная схема следящей системы

По функциональной схеме, приведенной на рис. 2, и передаточным функциям элементов составим исходную структурную схему следящей системы.



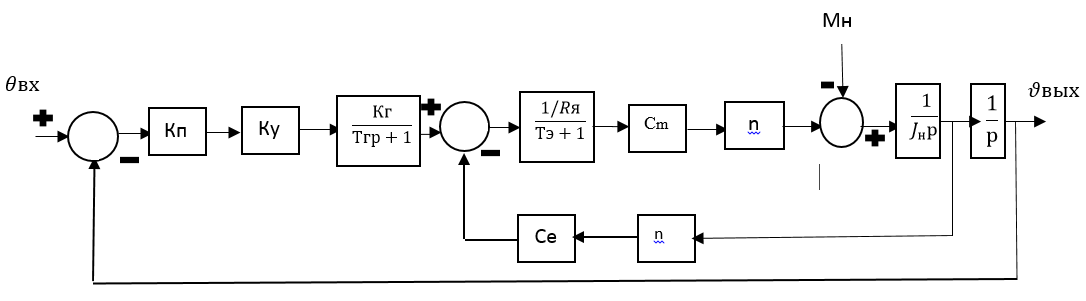
Рис. 2.1 – Структурная схема следящей системы



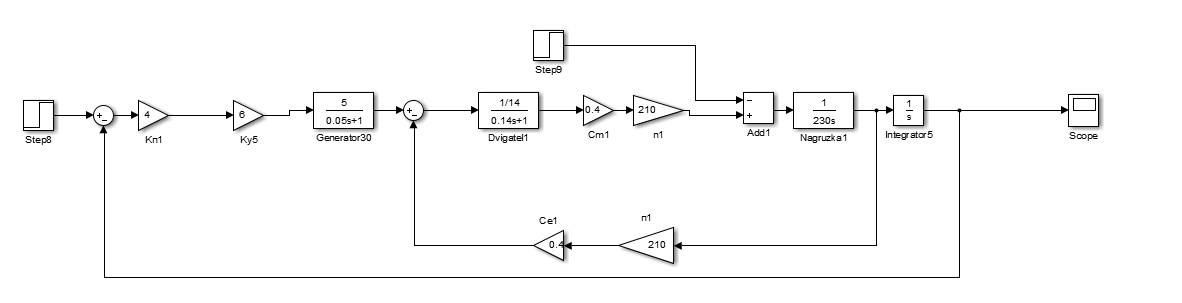
Рис. 2.2 – Структурная схема следящей системы Mathlab

Выполним преобразование структурной схемы. Перенесем возмущающий момент сил на сумматор местной обратной связи (рис. 2.3).



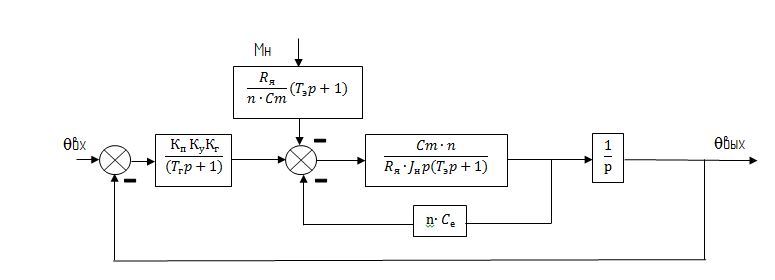
Рис. 2.3 – Преобразованная структурная схема

Упростим структурную схему рис.2.3, обозначим 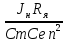= 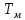и будем считать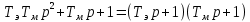



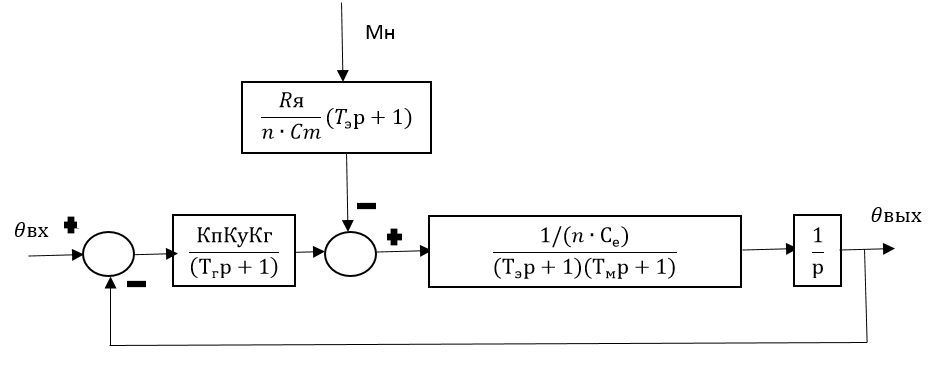
Рис. 2.4 – Упрощенная структурная схема

Перенесем возмущающий момент сил 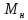на вход (рис.2.5):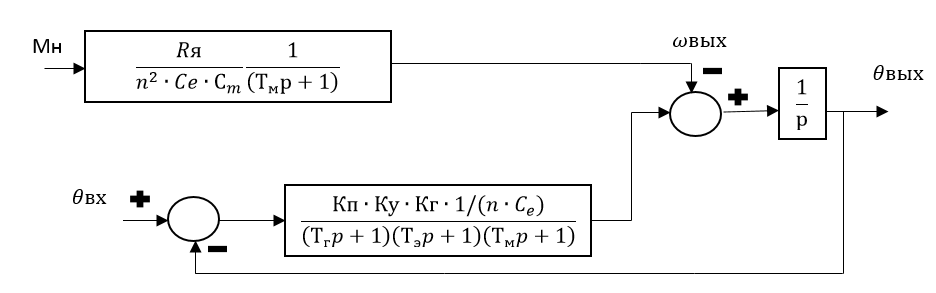



Рис.2.5



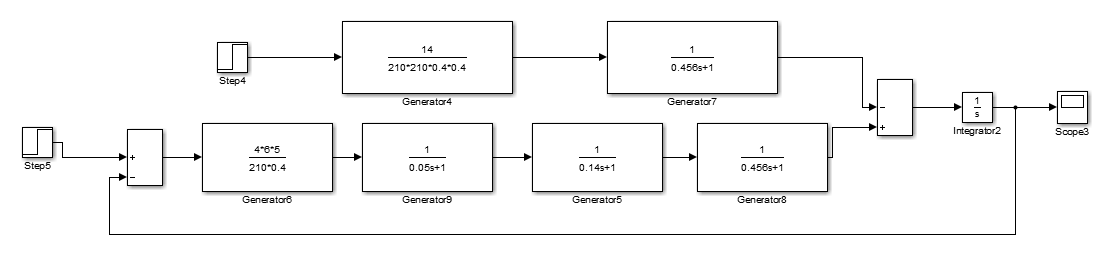
Рис.2.6

В задании варианта 4 необходимо исследовать влияние возмущающего момента сил 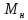=1∙(t) на угол поворота выходного вала . Для этого обнулим входной угол = 0 , тогда структурная схема примет вид (рис. 2.7):

---

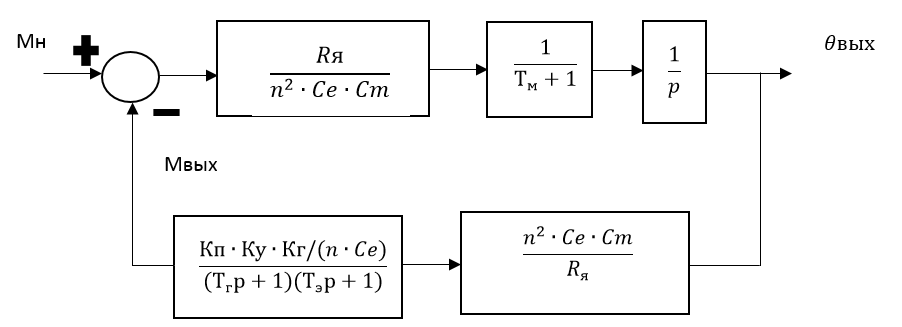
Рис. 2.7



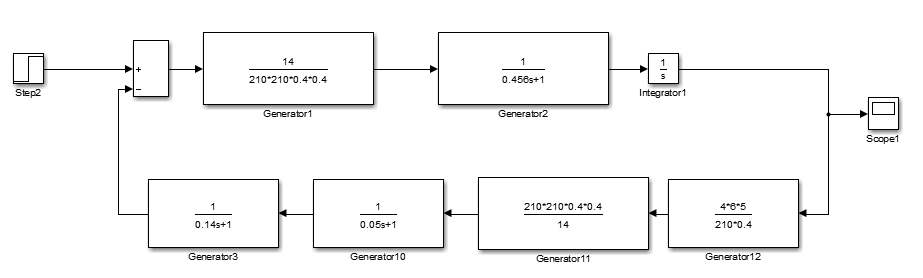
Рис.2.8

Упростим структурную схему (рис.2.9):



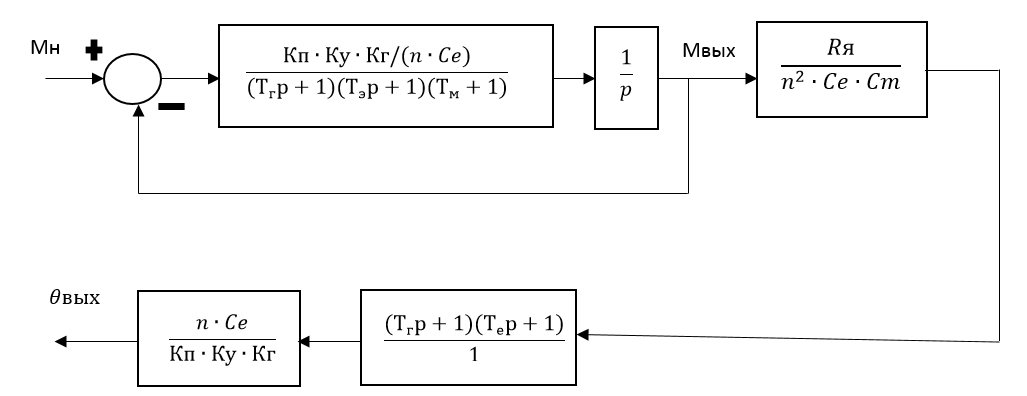
Рис. 2.9

Сократим всё необходимое, заменим 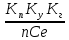= 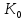, обозначим 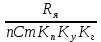= 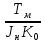и получим схему для исследования влияния возмущающего момента сил на угол поворота выходного вала (рис.2.8).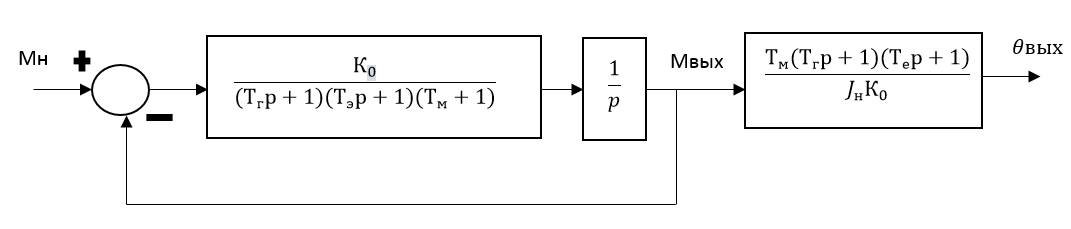



Рис. 2.10 – Структурная схема для исследования влияния возмущающего момента сил на угол поворота выходного вала (t)



Рис. 2.11 – Структурная схема для исследования влияния возмущающего момента сил на угол поворота выходного вала в программе Mathlab

Используя структурную схему, представленную на рис. 2.11, запишем три передаточные функции.

Передаточная функция разомкнутой следящей системы :

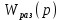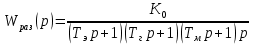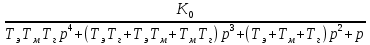= ; (3)

Передаточная функция замкнутой следящей системы по моменту :

= =

---

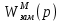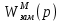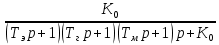Смотрите также файлы

• Методические рекомендации по суммативному оцениванию Информатика 7.pdf

• 1 Общая часть 1 Краткое описание технологического процесса.docx

• Лекция 1 по ms word 2007 Редактирование и форматирование документов Оглавление 1Свойства документа 2.docx

• Практическое задание 5 по учебному курсу Предпринимательская деятельность.docx

• Закон рк Об образовании.pptx