Файл: Курсовая работа по дисциплине Общая и прикладная теория автоматического управления на тему Анализ и синтез динамики следящей системы.docx
Добавлен: 06.12.2023
Просмотров: 113
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
; (4)
Передаточная функция замкнутой следящей системы по углу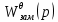 :
: 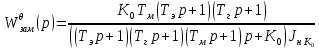 =
=
=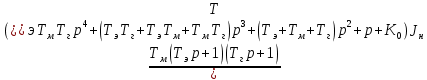 =
=
=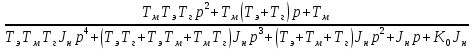 . (5)
. (5)
Данные передаточные функции позволяют провести анализ динамики следящей системы, а именно исследовать устойчивость, установившейся режим, построить ЛАЧХ и ЛФЧХ системы.
3. Анализ динамики системы
3.1. Исследование устойчивости движения следящей системы по критерию Гурвица
Алгебраический критерий Гурвица позволяет судить об устойчивости линейной системы по коэффициентам характеристического уравнения замкнутой САУ
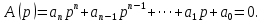
Формулировка критерия:
Для того, чтобы система была устойчивой, необходимо и достаточно, чтобы все коэффициенты характеристического уравнения системы, а также старший определитель Гурвица и все его диагональные миноры были бы положительные.
Правило записи старшего определителя:
В верхней строчке записываются по порядку коэффициенты с нечётными индексами, начиная с а1. Главная диагональ заполняется от аn-1 до а0. Столбцы заполняются сверху вниз от коэффициента с большим индексом к коэффициенту с меньшим индексом. На места недостающих коэффициентов ставятся нули.
Полином знаменателя замкнутой следящей системы имеет вид:
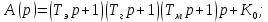 (6)
(6)
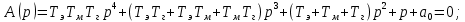
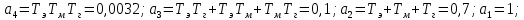
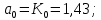
Тогда полином знаменателя передаточной функции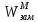 примет вид:
примет вид:
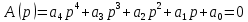 ; (7)
; (7)
Все коэффициенты характеристического уравнения замкнутой системы положительны.
Запишем старший определитель Гурвица:
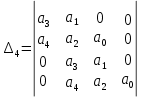 =
=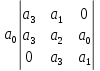 =
= 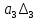
Определитель четвертого порядка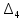 будет положительным, если положительны определитель третьего порядка и
будет положительным, если положительны определитель третьего порядка и 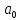 . Коэффициент
. Коэффициент 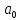 положителен исходя из формулы (6), следовательно проверим определитель третьего порядка
положителен исходя из формулы (6), следовательно проверим определитель третьего порядка 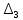 .
.
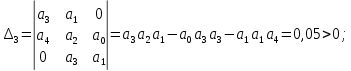
Так как определитель третьего порядка положителен, следовательно определитель четвертого порядка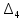 тоже положителен.
тоже положителен.
Посчитаем определители второго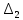 и первого
и первого 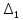 порядка:
порядка:
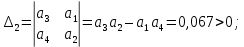
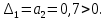
Так как все коэффициенты характеристического уравнения и определители Гурвица положительны, то делаем вывод, что следящая система устойчива.
3.2. Исследование устойчивости движения следящей системы по критерию Михайлова
Критерий Михайлова относится к графическим критериям. Он позволяет судить об устойчивости САУ любого порядка по годографу характеристического полинома
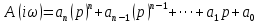 ,
,
который при замене p =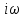 примет вид:
примет вид:
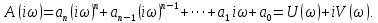
Годограф характеристического многочлена, который описывает вектор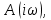 который строится в координатах
который строится в координатах 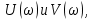 а
а 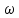 меняется от 0 до
меняется от 0 до 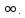
Формулировка критерия:
Для того, чтобы система была устойчивой, необходимо и достаточно, чтобы вектор характеристического полинома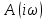 при изменении
при изменении  от 0 до
от 0 до 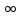 повернулся в положительном направлении на угол
повернулся в положительном направлении на угол 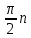 , где n – порядок характеристического уравнения.
, где n – порядок характеристического уравнения.
Характеристический полином следящей системы определяется по формуле (7):
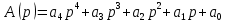 .
.
Произведём замену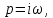 тогда полином примет вид
тогда полином примет вид
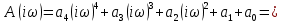
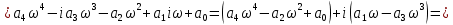
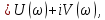
где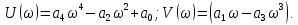
Определяем точки пересечения годографа Михайлова с осями координат.
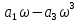 =0;
=0;
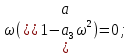
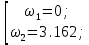
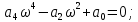
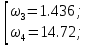
Таблица 2. Опорные точки для построения годографа Михайлова
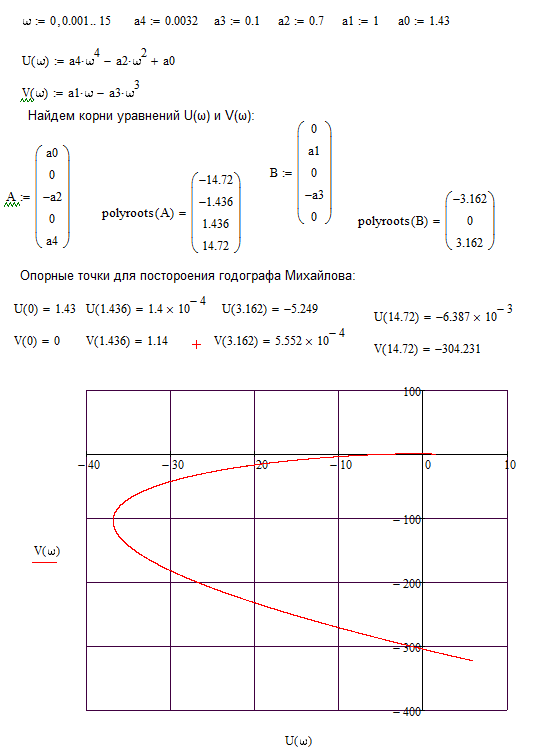
Рис. 3 – Годограф Михайлова для следящей системы
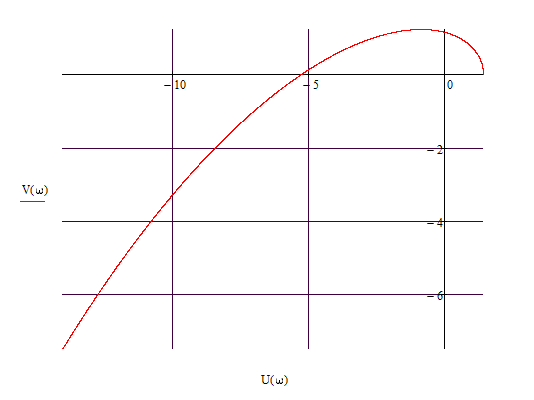
Рис. 3.1 – Годограф Михайлова для следящей системы при малых частотах
Годограф Михайлова начинает свое движения с точки (1.43;0), расположенной на действительной оси, двигаясь против часовой стрелки, последовательно проходит 4 квадранта координатной плоскости. При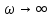 годограф мнимую и ось уходит в минус бесконечность в четвертом квадранте. Таким образом система 4 порядка устойчива.
годограф мнимую и ось уходит в минус бесконечность в четвертом квадранте. Таким образом система 4 порядка устойчива.
3.3. Исследование устойчивости движения следящей системы по критерию Найквиста
Частотный критерий Найквиста позволяет судить об устойчивости замкнутой системы по АФЧХ разомкнутой системы, которая строится в координатах действительной и мнимой части.
Формулировка критерия:
Для того, чтобы замкнутая САУ была устойчива, необходимо и достаточно, чтобы АФЧХ разомкнутой САУ не охватывала точку (-1;0i), т. е. пересекала действительную ось в диапазоне от -1 до 0.
Передаточная функция разомкнутой следящей системы:
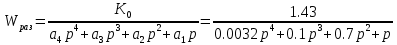
Проверяем устойчивость движения следящей системы с помощью программы Matlab.
Годограф разомкнутой следящей системы изображён на рис. 3.2.
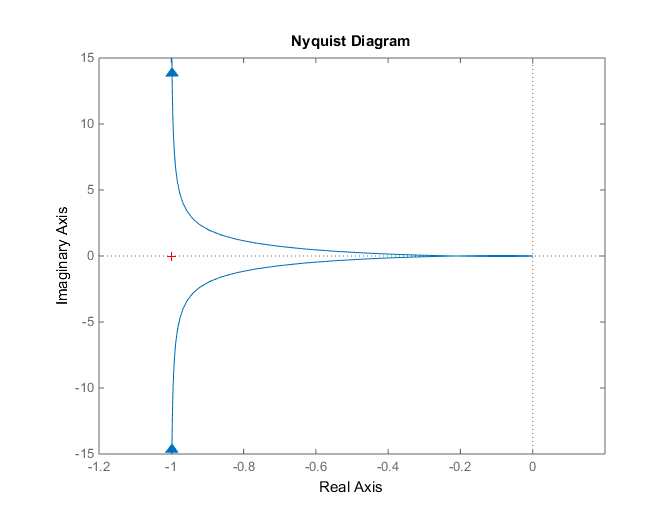
Рис. 3.2 – Годограф Найквиста для следящей системы
Анализируя полученный график, имеем следующее: годограф комплексной частотной характеристики (АФХ) разомкнутой следящей системы при изменении частоты от 0 до не охватывает на комплексной плоскости точку с координатами (-1; j0). Значит, следящая система устойчива.
не охватывает на комплексной плоскости точку с координатами (-1; j0). Значит, следящая система устойчива.
3.4. Исследование переходного режима следящей системы. Определение установившегося значения выходной величины
На практике переходный процесс можно считать завершённым, когда экспоненциальные составляющие станут настолько малыми, что полное решение уравнения лишь незначительно (обычно 5% от максимального значения соответствующей функции) будет отличаться от его частного решения, определяющего вынужденное движение САУ.
Точность САУ в установившемся режиме характеризуется ошибками системы при различных воздействиях – постоянном (единичном ступенчатом), а также изменяющихся по определённым законам. Для вычисления установившихся значений пользуются теоремой из операционного исчисления о предельном значении функции. Данная теорема утверждает, что если x(t) есть оригинал изображения X(p) и функция pX(p) – аналитична на мнимой оси и не имеет корней в правой полуплоскости, то
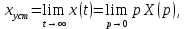
где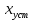 – установившееся значение функции
– установившееся значение функции 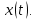
Если выходной сигнал θвых(p) представить в виде произведения передаточной функции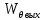 (p) и входного сигнала
(p) и входного сигнала  , то получим, что
, то получим, что
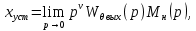
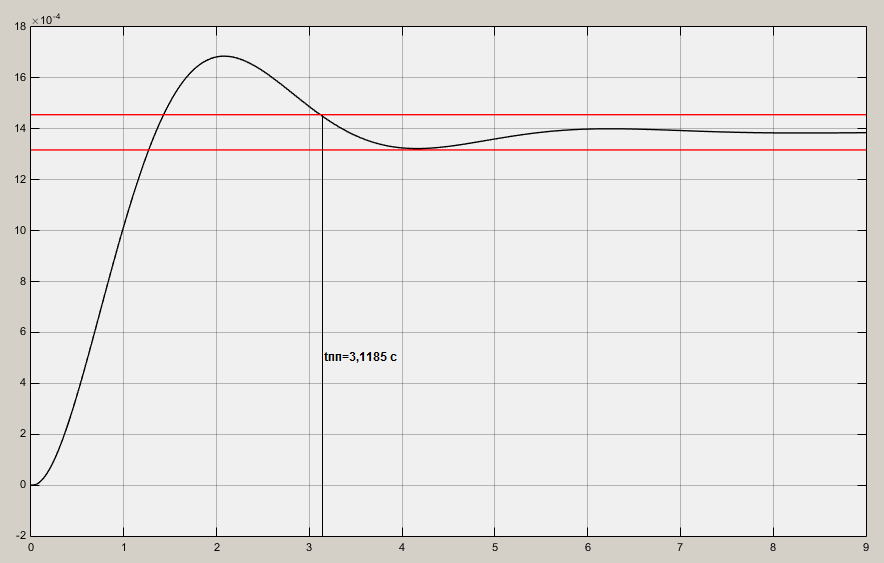
где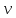 – порядок астатизма системы (в нашем случае
– порядок астатизма системы (в нашем случае 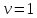 ).
).
При ступенчатом воздействии ( (t)=1(t)) изображение входного сигнала равно
(t)=1(t)) изображение входного сигнала равно
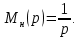
Установившееся значение выходной величины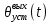 при ступенчатом воздействии
при ступенчатом воздействии 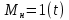 равняется:
равняется: 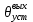 =
=
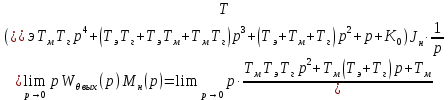 =
= 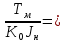 0,001386 рад (8)
0,001386 рад (8)
Передаточная функция замкнутой следящей системы по углу
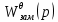 :
: 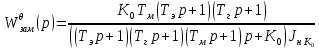 =
==
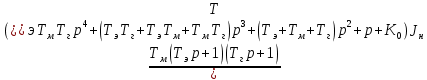 =
= =
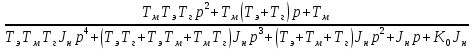 . (5)
. (5)Данные передаточные функции позволяют провести анализ динамики следящей системы, а именно исследовать устойчивость, установившейся режим, построить ЛАЧХ и ЛФЧХ системы.
3. Анализ динамики системы
3.1. Исследование устойчивости движения следящей системы по критерию Гурвица
Алгебраический критерий Гурвица позволяет судить об устойчивости линейной системы по коэффициентам характеристического уравнения замкнутой САУ
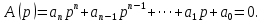
Формулировка критерия:
Для того, чтобы система была устойчивой, необходимо и достаточно, чтобы все коэффициенты характеристического уравнения системы, а также старший определитель Гурвица и все его диагональные миноры были бы положительные.
Правило записи старшего определителя:
В верхней строчке записываются по порядку коэффициенты с нечётными индексами, начиная с а1. Главная диагональ заполняется от аn-1 до а0. Столбцы заполняются сверху вниз от коэффициента с большим индексом к коэффициенту с меньшим индексом. На места недостающих коэффициентов ставятся нули.
Полином знаменателя замкнутой следящей системы имеет вид:
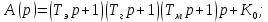 (6)
(6)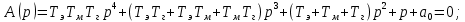
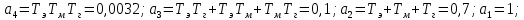
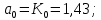
Тогда полином знаменателя передаточной функции
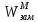 примет вид:
примет вид: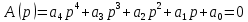 ; (7)
; (7)Все коэффициенты характеристического уравнения замкнутой системы положительны.
Запишем старший определитель Гурвица:
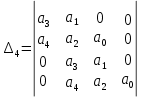 =
=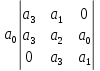 =
= 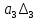
Определитель четвертого порядка
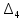 будет положительным, если положительны определитель третьего порядка и
будет положительным, если положительны определитель третьего порядка и 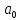 . Коэффициент
. Коэффициент 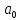 положителен исходя из формулы (6), следовательно проверим определитель третьего порядка
положителен исходя из формулы (6), следовательно проверим определитель третьего порядка 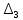 .
.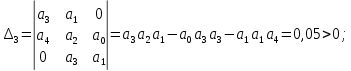
Так как определитель третьего порядка положителен, следовательно определитель четвертого порядка
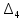 тоже положителен.
тоже положителен.Посчитаем определители второго
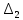 и первого
и первого 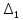 порядка:
порядка: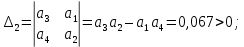
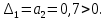
Так как все коэффициенты характеристического уравнения и определители Гурвица положительны, то делаем вывод, что следящая система устойчива.
3.2. Исследование устойчивости движения следящей системы по критерию Михайлова
Критерий Михайлова относится к графическим критериям. Он позволяет судить об устойчивости САУ любого порядка по годографу характеристического полинома
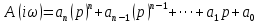 ,
, который при замене p =
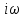 примет вид:
примет вид: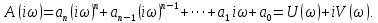
Годограф характеристического многочлена, который описывает вектор
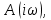 который строится в координатах
который строится в координатах 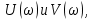 а
а 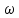 меняется от 0 до
меняется от 0 до 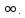
Формулировка критерия:
Для того, чтобы система была устойчивой, необходимо и достаточно, чтобы вектор характеристического полинома
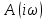 при изменении
при изменении  от 0 до
от 0 до 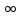 повернулся в положительном направлении на угол
повернулся в положительном направлении на угол 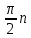 , где n – порядок характеристического уравнения.
, где n – порядок характеристического уравнения.Характеристический полином следящей системы определяется по формуле (7):
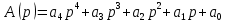 .
.Произведём замену
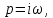 тогда полином примет вид
тогда полином примет вид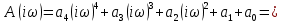
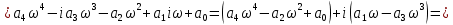
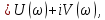
где
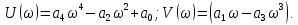
Определяем точки пересечения годографа Михайлова с осями координат.
-
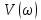 = 0;
= 0;
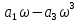 =0;
=0;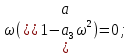
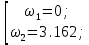
-
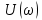 = 0;
= 0;
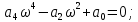
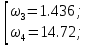
Таблица 2. Опорные точки для построения годографа Михайлова
| ω | 0 | 1,436 | 3.162 | 14.72 |
| U(ω) | 1,43 | 1.4∙ 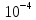 | –5.249 | -6.387∙ 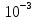 |
| V(ω) | 0 | 1.14 | 5.552∙ 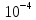 | -304.231 |

Рис. 3 – Годограф Михайлова для следящей системы

Рис. 3.1 – Годограф Михайлова для следящей системы при малых частотах
Годограф Михайлова начинает свое движения с точки (1.43;0), расположенной на действительной оси, двигаясь против часовой стрелки, последовательно проходит 4 квадранта координатной плоскости. При
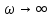 годограф мнимую и ось уходит в минус бесконечность в четвертом квадранте. Таким образом система 4 порядка устойчива.
годограф мнимую и ось уходит в минус бесконечность в четвертом квадранте. Таким образом система 4 порядка устойчива.3.3. Исследование устойчивости движения следящей системы по критерию Найквиста
Частотный критерий Найквиста позволяет судить об устойчивости замкнутой системы по АФЧХ разомкнутой системы, которая строится в координатах действительной и мнимой части.
Формулировка критерия:
Для того, чтобы замкнутая САУ была устойчива, необходимо и достаточно, чтобы АФЧХ разомкнутой САУ не охватывала точку (-1;0i), т. е. пересекала действительную ось в диапазоне от -1 до 0.
Передаточная функция разомкнутой следящей системы:
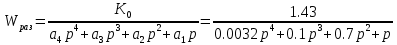
Проверяем устойчивость движения следящей системы с помощью программы Matlab.
Годограф разомкнутой следящей системы изображён на рис. 3.2.

Рис. 3.2 – Годограф Найквиста для следящей системы
Анализируя полученный график, имеем следующее: годограф комплексной частотной характеристики (АФХ) разомкнутой следящей системы при изменении частоты от 0 до
 не охватывает на комплексной плоскости точку с координатами (-1; j0). Значит, следящая система устойчива.
не охватывает на комплексной плоскости точку с координатами (-1; j0). Значит, следящая система устойчива.3.4. Исследование переходного режима следящей системы. Определение установившегося значения выходной величины
На практике переходный процесс можно считать завершённым, когда экспоненциальные составляющие станут настолько малыми, что полное решение уравнения лишь незначительно (обычно 5% от максимального значения соответствующей функции) будет отличаться от его частного решения, определяющего вынужденное движение САУ.
Точность САУ в установившемся режиме характеризуется ошибками системы при различных воздействиях – постоянном (единичном ступенчатом), а также изменяющихся по определённым законам. Для вычисления установившихся значений пользуются теоремой из операционного исчисления о предельном значении функции. Данная теорема утверждает, что если x(t) есть оригинал изображения X(p) и функция pX(p) – аналитична на мнимой оси и не имеет корней в правой полуплоскости, то
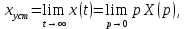
где
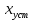 – установившееся значение функции
– установившееся значение функции 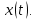
Если выходной сигнал θвых(p) представить в виде произведения передаточной функции
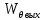 (p) и входного сигнала
(p) и входного сигнала  , то получим, что
, то получим, что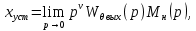
где
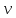 – порядок астатизма системы (в нашем случае
– порядок астатизма системы (в нашем случае 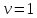 ).
).При ступенчатом воздействии (
 (t)=1(t)) изображение входного сигнала равно
(t)=1(t)) изображение входного сигнала равно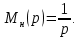
Установившееся значение выходной величины
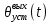 при ступенчатом воздействии
при ступенчатом воздействии 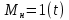 равняется:
равняется: 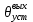 =
=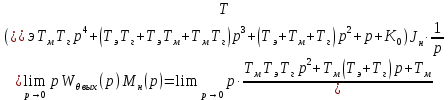 =
= 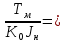 0,001386 рад (8)
0,001386 рад (8)