Файл: Курсовая работа по дисциплине Общая и прикладная теория автоматического управления на тему Анализ и синтез динамики следящей системы.docx
Добавлен: 06.12.2023
Просмотров: 115
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
: 
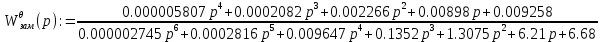
5. Анализ динамики скорректированной системы
5.1. Исследование устойчивости движения скорректированной следящей системы по критерию Найквиста
Передаточная функция разомкнутой следящей системы после коррекции:
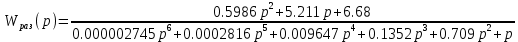
Проверяем устойчивость движения следящей системы с помощью программы Matlab.
Годограф разомкнутой следящей системы изображён на рис. 5
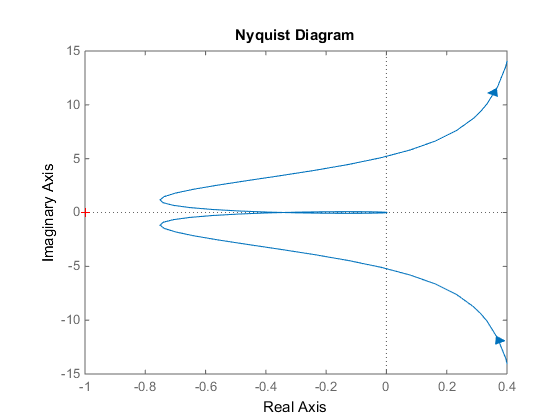
Рис. 5 – Годограф Найквиста для скорректированной следящей системы
Анализируя полученный график, имеем следующее: годограф комплексной частотной характеристики (АФХ) разомкнутой следящей системы при изменении частоты от 0 до
не охватывает на комплексной плоскости точку с координатами (-1; j0). Значит, следящая система устойчива.
5.2. Исследование переходного режима скорректированной следящей системы.
Установившееся значение выходной величины
при ступенчатом воздействии 
равняется: 
=
= 
0,001386 рад
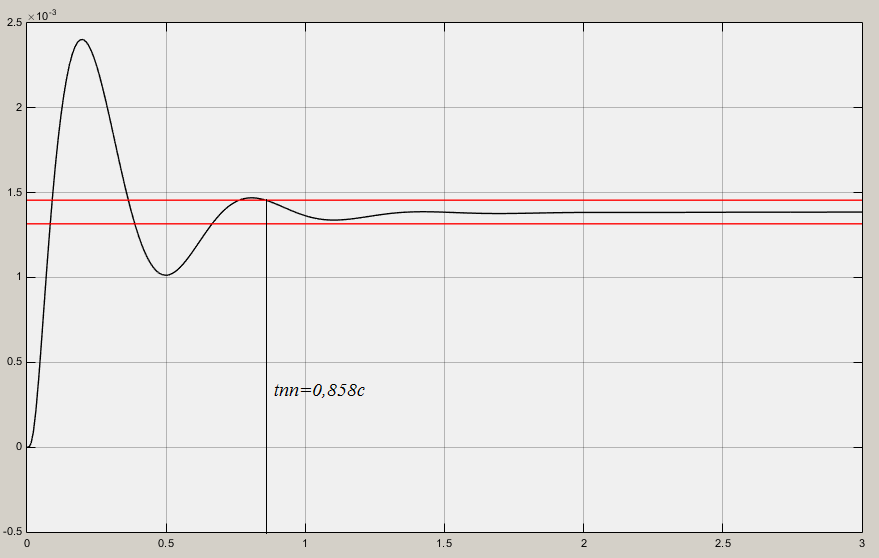
Рис. 5.1 – Выходной сигнал
при ступенчатом воздействии
Определим время переходного процесса и величину перерегулирования.
Время переходного процесса по
(t) составляет 0.858 с.
Величина перерегулирования по
(t) составляет
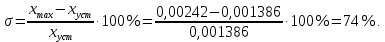
Установившееся значение выходной величины
при ступенчатом воздействии равняется:
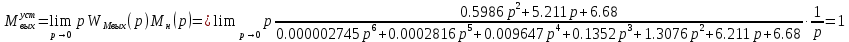Н*м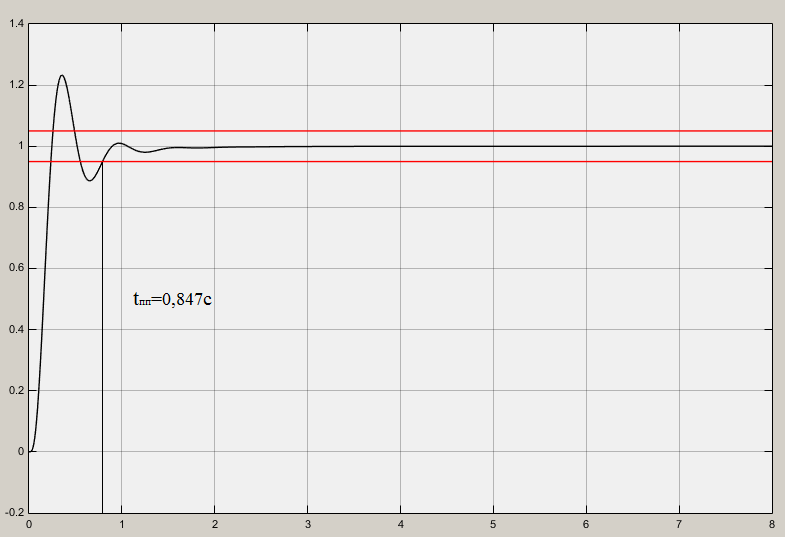
Рис. 5.2 – Выходной сигнал при ступенчатом воздействии
Из графика, приведенного на рис.5.2, находим установившееся значение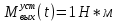
. Это значение соответствует расчетам из формулы, приведенной выше.
Определим время переходного процесса и величину перерегулирования.
Время переходного процесса по составляет 0,847 с.
Величина перерегулирования по составляет
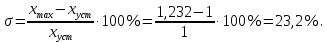
5.3 Частотный анализ скорректированной следящей системы
Для проведения частотного анализа построим ЛАФЧХ разомкнутой скорректированной следящей системы
(рис. 5.3).
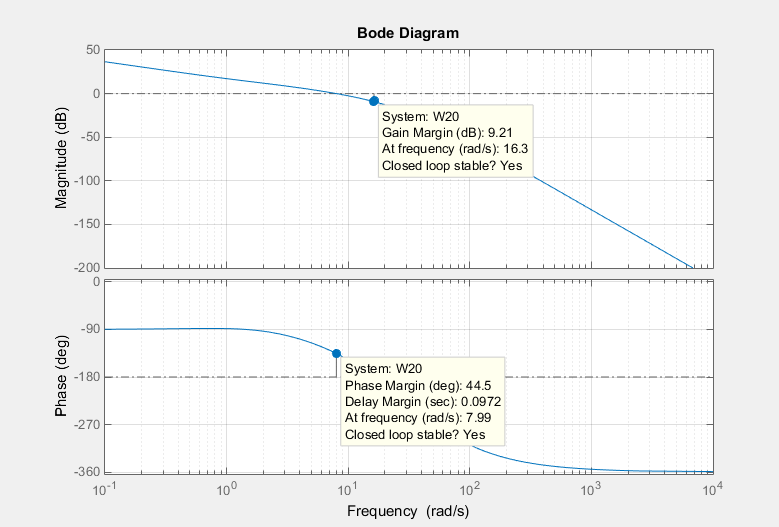
Рис.5.3 ЛАФЧХ разомкнутой скорректированной следящей системы
Из рис. 3.5 видно, что ЛАЧХ разомкнутой системы пересекает 0 дБ до частоты, при которой ЛФЧХ пересекает – 180○. Следовательно, разомкнутая система устойчива. Запасы устойчивости по амплитуде и фазе равны соответственно:
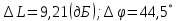
Используя передаточную функцию замкнутой системы
построим ЛАФЧХ замкнутой скорректированной системы (рис. 5.4), которая показывает, как следящая система реагирует на гармонический возмущающий момент.
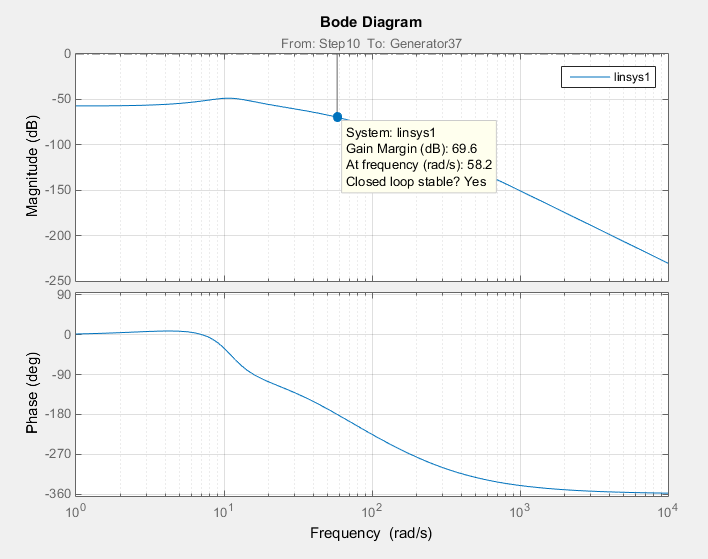
Рис. 5.4 – ЛАФЧХ замкнутой скорректированной следящей системы
Заключение
В данной курсовой работе, целью которой являлось проведение анализа и синтеза следящей системы, были выполнены все поставленные задачи.
Объяснён принцип работы следящей системы и её составных частей.
Построена математическая модель следящей системы, в ходе построения которой:
– была составлена функциональная схема;
– были записаны уравнения движения;
–были найдены передаточные функции элементов системы, а также передаточные функции разомкнутой и замкнутой следящей системы;
– была составлена и построена структурная схема следящей системы.
Проведён полный динамический анализ следящей системы, в котором проводилась проверка тремя критериями устойчивости, в ходе которой было определено, что данная САУ является устойчивой; исследован переходный процесс разомкнутой и замкнутой следящей системы; проведён частотный анализ ЛАФЧХ разомкнутой системы.
Проведён синтез корректирующего звена, в ходе которого были оптимизированы время переходного процесса, величина перерегулирования, запасы по фазе и амплитуде.
Проведён анализ скорректированной следящей системы, в котором проводилась проверка устойчивости скорректированной системой методом Найквиста; был исследован переходный процесс разомкнутой скорректированной следящей системы.
В ходе данной работы были освоены навыки проведения динамического синтеза САУ, основанного на построении желаемой ЛАЧХ. Объектом исследования в данной курсовой работе являлась следящая система которая управляет углом поворота нагрузки с помощью двигателя постоянного тока и редуктора, путем подачи на его вход момента. Так как желаемая ЛАЧХ строится по разомкнутой системе САУ, а ЛАЧХ корректирующего звена строится вычитанием располагаемой ЛАЧХ из желаемой ЛАЧХ САУ, мы удовлетворяем все требования к качеству переходного процесса следящей системы по моменту. Исходя из этого мы получаем такие показатели САУ: время переходного процесса по
составляет 0,847 с; величина перерегулирования по составляет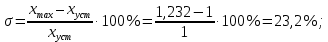 
запасы устойчивости по амплитуде и фазе равны соответственно: 
. Эти показатели качества полностью удовлетворяют данные технического задания.
Так как метод, по которому был проведен синтез САУ, основан на построении желаемой ЛАЧХ, которая строится по разомкнутой системе по возмущающему моменту, мы не можем полностью удовлетворить требования показателей САУ замкнутой системы по углу поворота выходной оси. Поэтому мы получаем следующие показатели следящей системы: время переходного процесса по (t) составляет 0.858 с; величина перерегулирования по составляет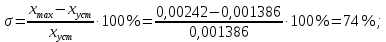 
а запасы устойчивости по амплитуде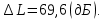 
Список используемой литературы
1. Родионов В. И., Телухин С. В. Теория автоматического управления. Анализ и синтез линейных систем: учеб. пособие. – Тула: Изд – во ТулГУ, 2014. – 124 с.
2. Теория систем автоматического управления / В. А. Бесекерский, Е. П. Попов. – Изд. 4 – е, перераб. и доп. – СПб, Изд – во «Профессия», 2003. – 752 с. – (Серия: Специалист)
3. Лазарев Ю. Ф. Моделирование процессов и систем в MATLAB: учебный курс / Ю. Лазарев. – СПб.: Питер, 2005. – 512 с.
4. Фалдин Н. В., Морозова Е. В. Специальные разделы математики (для специалистов по автоматическому управлению): учебное пособие / Н. В. Фалдин, Е. В. Морозова; ТулГУ. – Тула: Изд – во ТулГУ, 2013. – 142 с.
5. Никулин Е. А. Основы теории автоматического управления. Частотные методы анализа и синтеза систем: учеб. пособие для вузов / Е. А. Никулин. – СПб.: БХВ – Петербург, 2004. – 640 с.
6. Макаров И. М., Менский Б. М. Линейные автоматические системы (элементы теории, методы расчёта и справочный материал). – 2 –е изд., перераб. и доп. – М.: Машиностроение, 1982. – 504 с.
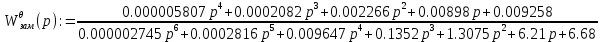
5. Анализ динамики скорректированной системы
5.1. Исследование устойчивости движения скорректированной следящей системы по критерию Найквиста
Передаточная функция разомкнутой следящей системы после коррекции:
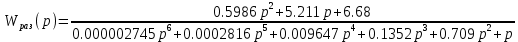
Проверяем устойчивость движения следящей системы с помощью программы Matlab.
Годограф разомкнутой следящей системы изображён на рис. 5
Рис. 5 – Годограф Найквиста для скорректированной следящей системы
Анализируя полученный график, имеем следующее: годограф комплексной частотной характеристики (АФХ) разомкнутой следящей системы при изменении частоты от 0 до
не охватывает на комплексной плоскости точку с координатами (-1; j0). Значит, следящая система устойчива.5.2. Исследование переходного режима скорректированной следящей системы.
Установившееся значение выходной величины
при ступенчатом воздействии равняется: = = 0,001386 рад Рис. 5.1 – Выходной сигнал
при ступенчатом воздействии Определим время переходного процесса и величину перерегулирования.
Время переходного процесса по
(t) составляет 0.858 с.Величина перерегулирования по
(t) составляет
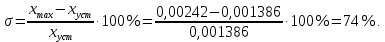
Установившееся значение выходной величины
при ступенчатом воздействии равняется: 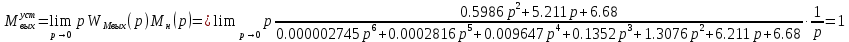Н*м Рис. 5.2 – Выходной сигнал
при ступенчатом воздействии Из графика, приведенного на рис.5.2, находим установившееся значение
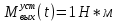. Это значение соответствует расчетам из формулы, приведенной выше.Определим время переходного процесса и величину перерегулирования.
Время переходного процесса по
составляет 0,847 с.Величина перерегулирования по
составляет 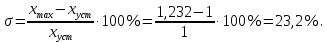5.3 Частотный анализ скорректированной следящей системы
Для проведения частотного анализа построим ЛАФЧХ разомкнутой скорректированной следящей системы
(рис. 5.3). Рис.5.3 ЛАФЧХ разомкнутой скорректированной следящей системы
Из рис. 3.5 видно, что ЛАЧХ разомкнутой системы пересекает 0 дБ до частоты, при которой ЛФЧХ пересекает – 180○. Следовательно, разомкнутая система устойчива. Запасы устойчивости по амплитуде и фазе равны соответственно:
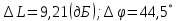
Используя передаточную функцию замкнутой системы
построим ЛАФЧХ замкнутой скорректированной системы (рис. 5.4), которая показывает, как следящая система реагирует на гармонический возмущающий момент.
Рис. 5.4 – ЛАФЧХ замкнутой скорректированной следящей системы
Заключение
В данной курсовой работе, целью которой являлось проведение анализа и синтеза следящей системы, были выполнены все поставленные задачи.
Объяснён принцип работы следящей системы и её составных частей.
Построена математическая модель следящей системы, в ходе построения которой:
– была составлена функциональная схема;
– были записаны уравнения движения;
–были найдены передаточные функции элементов системы, а также передаточные функции разомкнутой и замкнутой следящей системы;
– была составлена и построена структурная схема следящей системы.
Проведён полный динамический анализ следящей системы, в котором проводилась проверка тремя критериями устойчивости, в ходе которой было определено, что данная САУ является устойчивой; исследован переходный процесс разомкнутой и замкнутой следящей системы; проведён частотный анализ ЛАФЧХ разомкнутой системы.
Проведён синтез корректирующего звена, в ходе которого были оптимизированы время переходного процесса, величина перерегулирования, запасы по фазе и амплитуде.
Проведён анализ скорректированной следящей системы, в котором проводилась проверка устойчивости скорректированной системой методом Найквиста; был исследован переходный процесс разомкнутой скорректированной следящей системы.
В ходе данной работы были освоены навыки проведения динамического синтеза САУ, основанного на построении желаемой ЛАЧХ. Объектом исследования в данной курсовой работе являлась следящая система которая управляет углом поворота нагрузки с помощью двигателя постоянного тока и редуктора, путем подачи на его вход момента. Так как желаемая ЛАЧХ строится по разомкнутой системе САУ, а ЛАЧХ корректирующего звена строится вычитанием располагаемой ЛАЧХ из желаемой ЛАЧХ САУ, мы удовлетворяем все требования к качеству переходного процесса следящей системы по моменту. Исходя из этого мы получаем такие показатели САУ: время переходного процесса по
составляет 0,847 с; величина перерегулирования по составляет 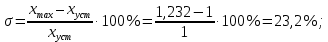запасы устойчивости по амплитуде и фазе равны соответственно: . Эти показатели качества полностью удовлетворяют данные технического задания.Так как метод, по которому был проведен синтез САУ, основан на построении желаемой ЛАЧХ, которая строится по разомкнутой системе по возмущающему моменту, мы не можем полностью удовлетворить требования показателей САУ замкнутой системы по углу поворота выходной оси. Поэтому мы получаем следующие показатели следящей системы: время переходного процесса по
(t) составляет 0.858 с; величина перерегулирования по составляет 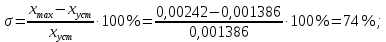а запасы устойчивости по амплитуде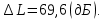 Список используемой литературы
1. Родионов В. И., Телухин С. В. Теория автоматического управления. Анализ и синтез линейных систем: учеб. пособие. – Тула: Изд – во ТулГУ, 2014. – 124 с.
2. Теория систем автоматического управления / В. А. Бесекерский, Е. П. Попов. – Изд. 4 – е, перераб. и доп. – СПб, Изд – во «Профессия», 2003. – 752 с. – (Серия: Специалист)
3. Лазарев Ю. Ф. Моделирование процессов и систем в MATLAB: учебный курс / Ю. Лазарев. – СПб.: Питер, 2005. – 512 с.
4. Фалдин Н. В., Морозова Е. В. Специальные разделы математики (для специалистов по автоматическому управлению): учебное пособие / Н. В. Фалдин, Е. В. Морозова; ТулГУ. – Тула: Изд – во ТулГУ, 2013. – 142 с.
5. Никулин Е. А. Основы теории автоматического управления. Частотные методы анализа и синтеза систем: учеб. пособие для вузов / Е. А. Никулин. – СПб.: БХВ – Петербург, 2004. – 640 с.
6. Макаров И. М., Менский Б. М. Линейные автоматические системы (элементы теории, методы расчёта и справочный материал). – 2 –е изд., перераб. и доп. – М.: Машиностроение, 1982. – 504 с.