Рис. 3.3 – Выходной сигнал 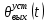при ступенчатом воздействии

Определим время переходного процесса и величину перерегулирования.

Время переходного процесса по 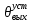(t) составляет 3,1185 с.

Величина перерегулирования по 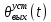составляет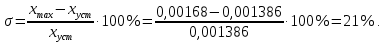



Установившееся значение выходной величины (t) при ступенчатом воздействии равняется: =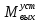

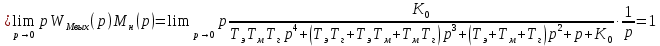Н*м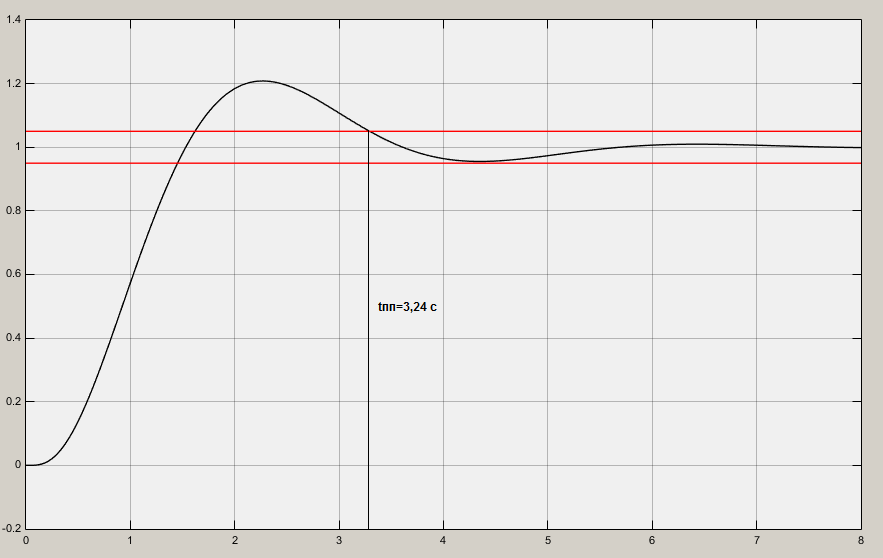



Рис. 3.4 – Выходной сигнал 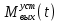при ступенчатом воздействии

Из графиков, приведенных на рис.3.3 и рис.3.4, находим установившееся значения угла поворота выходного вала =0,001386 рад и 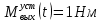. Эти значения соответствуют расчетам из формул (8) и (9) соответственно.

Определим время переходного процесса и величину перерегулирования.

Время переходного процесса по 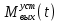составляет 3,24 с.

Величина перерегулирования по 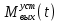составляет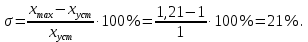

---

3.5. Частотный анализ следящей системы

Для проведения частотного анализа построим ЛАФЧХ разомкнутой следящей системы (рис. 3.5).



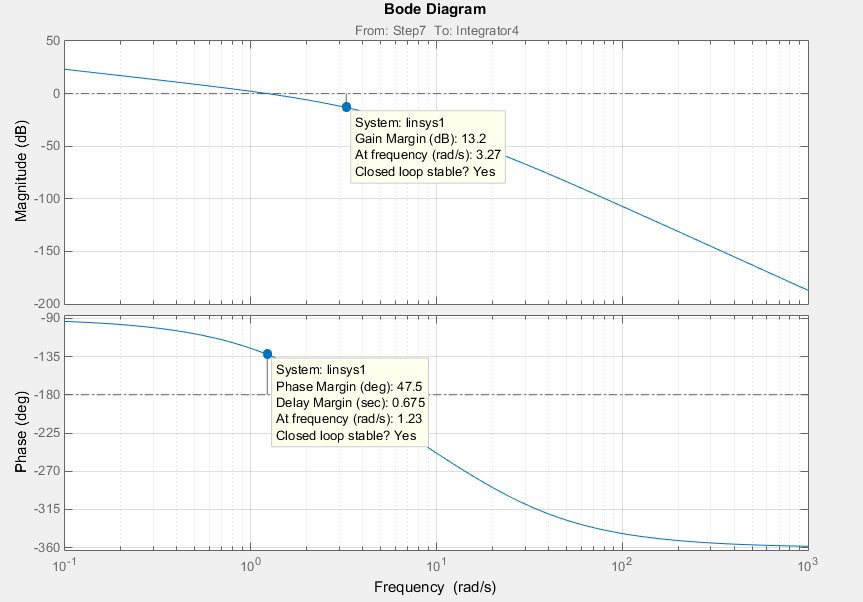
Рис. 3.5 – ЛАФЧХ разомкнутой следящей системы

Из рис. 3.5 видно, что ЛАЧХ разомкнутой системы пересекает 0 дБ до частоты, при которой ЛФЧХ пересекает – 180^○. Следовательно, разомкнутая система устойчива. Запасы устойчивости по амплитуде и фазе равны соответственно:



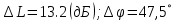
Используя передаточную функцию замкнутой системы построим ЛАФЧХ замкнутой системы (рис. 3.6), которая показывает, как следящая система реагирует на гармонический возмущающий момент.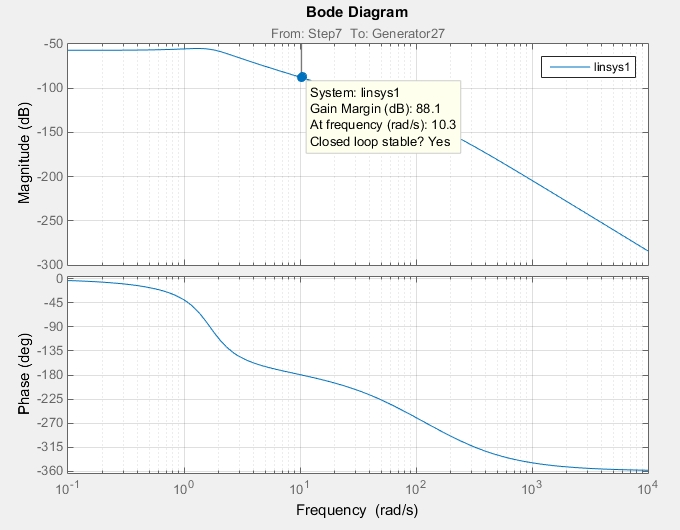



Рис. 3.6 – ЛАФЧХ замкнутой следящей системы

Из рис. 3.6 видно, что рабочей частотой следящей системы является -50 Дб.

Проведенные исследования показывают, что следящая система не удовлетворяет требованиям технического задания, поэтому необходимо уменьшать ее динамические характеристики с помощью структурного синтеза и введением дополнительных корректирующих звеньев.

4. Синтез динамики следящей системы

4.1. Построение желаемой ЛАФЧХ

Широкое применение при синтезе САУ нашёл метод логарифмических частотных характеристик. Этот метод обладает достаточной простотой и наглядностью. Идея метода основана на известной связи между переходным процессом и ЛАЧХ. Зная желаемый вид переходного процесса, можно легко построить соответствующую такому процессу желаемую ЛАЧХ. Далее у виду желаемой ЛАЧХ приближают ЛАЧХ располагаемой системы.

Желаемая ЛАЧХ разомкнутой САУ строится исходя из требования, предъявляемых к САУ. Основными из них считаются: коэффициент усиления, порядок астатизма, время переходного процесса, запасы устойчивости по амплитуде и фазе.

Желаемую ЛАЧХ можно разделить на три части: низкочастотную, среднечастотную и высокочастотную. Низкочастотная часть определяет точность работы системы, которая зависит от общего коэффициента усиления и порядка её астатизма. Наклон низкочастотного отрезка определяется величиной –20

---

ν дБ/дек, где ν – порядок астатизма системы. Указанный начальный отрезок характеристики должен проходить через точку с ординатой 20lgk, на частоте равной 1, где k – требуемый коэффициент разомкнутой САУ.

Среднечастотная часть желаемой ЛАЧХ определяет качество регулирования системы. Установлено, что оптимальный наклон в области частоты среза (ω_с) равен –20 дБ/дек. Выбираем частоту среза желаемой ЛАЧХ.

Высокочастотная асимптота ЛАЧХ мало влияет на вид переходного процесса, то для этого, чтобы не усложнять корректирующее устройство, она выбирается аналогичной ЛАЧХ исходной некорректированной системы.
Для определения _c воспользуемся монограммой Солодовникова, приведенной на рис. 4.



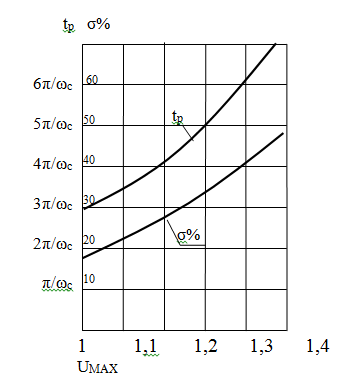
Рис. 4– Монограмма Солодовникова
Значению %= 21% соответствует 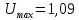. Из графика 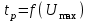по известному значению 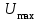найдем значение времени регулирования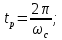



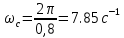
Таким образом, _с должна находиться не раньше чем 7.85 .

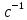Примем .

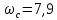
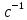Для определения ширины центрального отрезка воспользуемся формулой

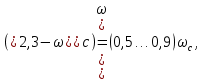
где 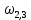– частоты, определящие ширину средней частоты желаемой ЛАЧХ.

Тогда получим:

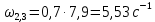. Приблизим полученное значение до 5,5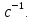

Построим желаемую ЛАФЧХ с помощью ручного корректирования ЛАФЧХ располагаемой системы в программе Matlab. В результате коррекции была получена ЛАФЧХ, представленная на рис. 4.1.



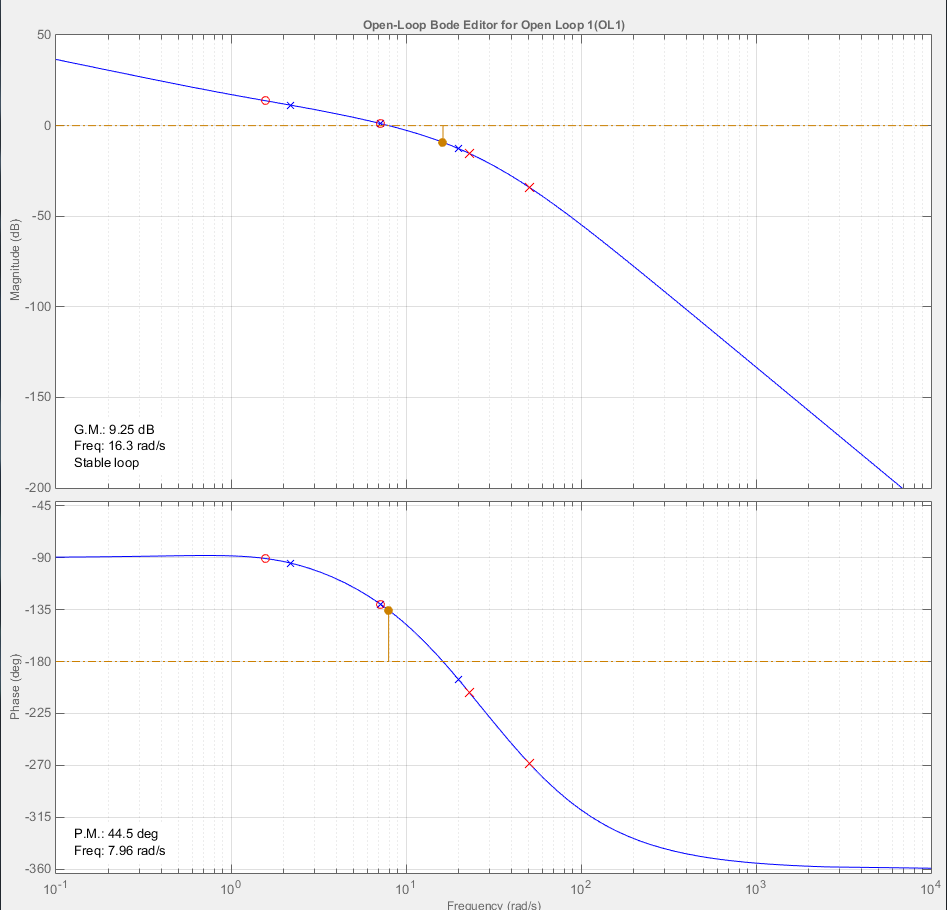
Рис. 4.1– Построение желаемой ЛАФЧХ в Matlab.

После построения желаемой ЛАФЧХ запасы по амплитуде и фазе составляют:

---

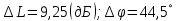
4.2. Получение передаточной функции корректирующего звена

С помощь пакета SISO Design программы Matlab получим передаточную функцию корректирующего звена (рис. 4.2).



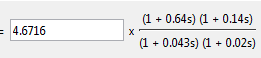
Рис.4.2 Передаточная функция корректирующего звена

4.3. Построение ЛАЧХ корректирующего звена

Коррекция была проведена методом синтеза последовательно корректирующего устройства. Включение корректирующего звена в основную цепь САУ последовательно с основными элементами показано на рис. 4.3.



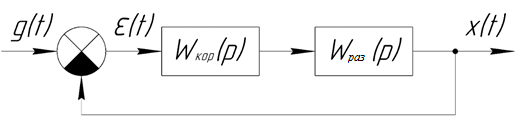
Рис. 4.3 – Структурная схема последовательной коррекции

По рисунку 4.3 можно записать передаточную функцию скорректированной САУ:



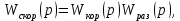
или



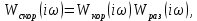
где 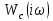– АФЧХ разомкнутой скорректированной системы. Запишем выражение для ЛАЧХ разомкнутой скорректированной САУ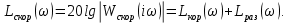



Таким образом ЛАЧХ корректирующего звена равняется



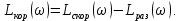
С помощью программы Matlab была получена ЛАЧХ корректирующего звена, представленная на рис. 4.4.



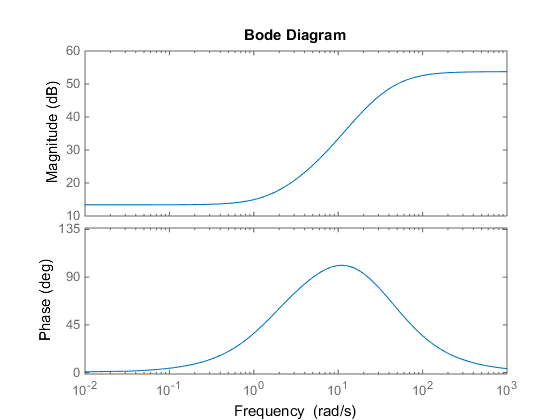
Рис. 4.4 – ЛАЧХ корректирующего звена

4.4. Переходный режим скорректированной следящей системы

График скорректированного переходного процесса следящей системы, который показывает момент по моменту приведён на рис. 4.5.



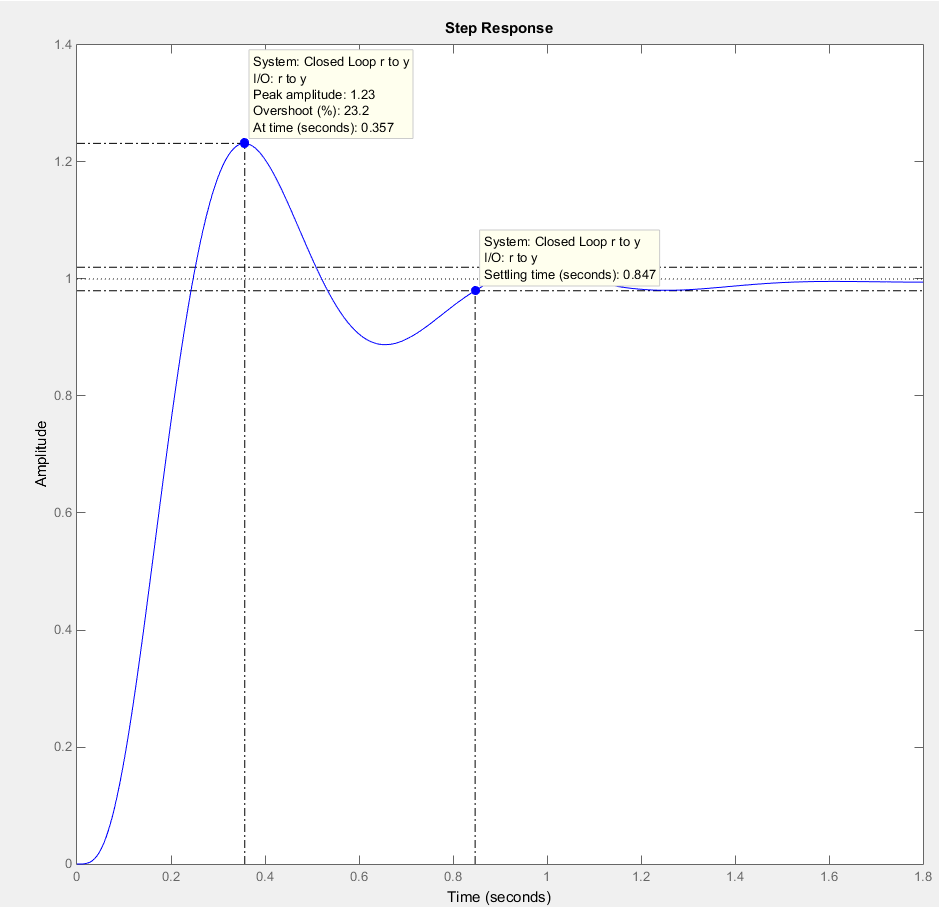
Рис. 4.5 – Переходный процесс после коррекции момент по моменту

Как видно из рис. 4.5, после синтеза корректирующего звена, время переходного процесса и величина составляют:

---

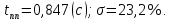
4.5. Структурная схема скорректированной следящей системы

Зная передаточную функцию корректирующего звена и передаточные функции элементов составим структурную схему скорректированной следящей системы рис.4.6.



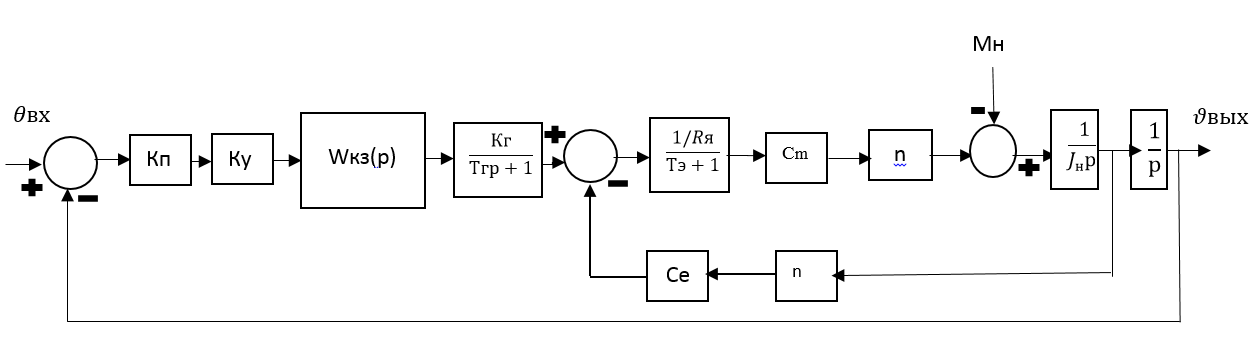
Рис.4.6 Структурная схема скорректированной следящей системы



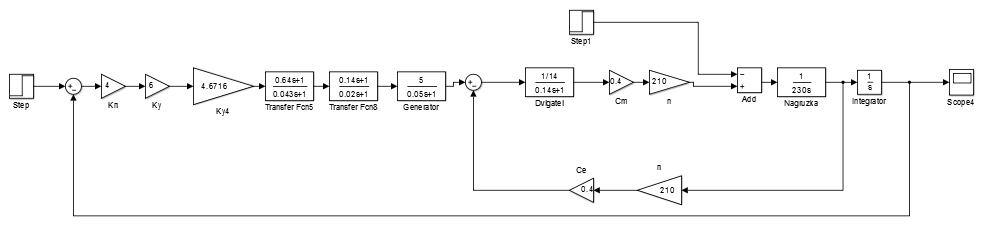
Рис.4.7 Структурная схема скорректированной следящей системы в Mathlab

Беря во внимание преобразования (рис.2.1-2.11), преобразуем структурную схему скорректированной следящей системы (рис.4.6) в структурная схема для исследования влияния возмущающего момента сил на угол поворота выходного вала рис.4.8.



Рис.4.8 Структурная схема для исследования влияния возмущающего момента сил на угол поворота выходного вала



Рис.4.8 Структурная схема для исследования влияния возмущающего момента сил на угол поворота выходного вала в системе Mathlab

Используя структурную схему, представленную на рис. 4.8, запишем передаточные функции скорректированной системы.

Передаточная функция разомкнутой следящей системы после коррекции:



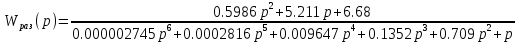
Передаточная функция замкнутой скорректированной следящей системы по моменту :



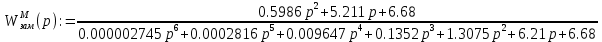
Передаточная функция замкнутой скорректированной следящей системы по углу

---

Смотрите также файлы

• Методические рекомендации по суммативному оцениванию Информатика 7.pdf

• 1 Общая часть 1 Краткое описание технологического процесса.docx

• Лекция 1 по ms word 2007 Редактирование и форматирование документов Оглавление 1Свойства документа 2.docx

• Практическое задание 5 по учебному курсу Предпринимательская деятельность.docx

• Закон рк Об образовании.pptx