Файл: Контрольная работа Вариант 22 Задачи С1, С2, К1, К2, Д1, Д2 Задача равновесие произвольной плоской системы сил.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 46
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Теоретическая механика
Контрольная работа
Вариант 22
Задачи С1, С2, К1, К2, Д1, Д2
Задача С1. Равновесие произвольной плоской системы сил
(Определение реакций опор твёрдого тела)
Найти реакции опор конструкции, схема которой изображена на рис. С1.0–С1.9. Необходимые исходные данные представлены в таблице С1.
Исходные данные:
Таблица С1
| Номер условия | 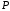 , ,кН | 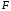 , ,кН | 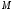 , ,кН·м | 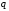 , ,кН/м | 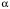 , ,град | 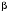 , ,град | 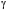 , ,град |
| 2 | 30 | 10 | 25 | 15 | 60 | 45 | 30 |
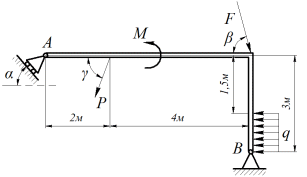
Рис.С1.2
Решение
1. Рассмотрим равновесие рамы.
Проведем координатные оси
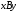 и изобразим действующие на конструкцию силы (рис.1): заданные силы
и изобразим действующие на конструкцию силы (рис.1): заданные силы 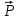 и
и 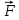 , пару сил с моментом
, пару сил с моментом 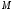 , равномерно распределенную нагрузку
, равномерно распределенную нагрузку 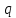 и реакции связей
и реакции связей 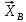 ,
, 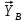 ,
, 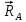 (реакцию шарнирно неподвижной опоры B изображаем двумя составляющими, направленными вдоль выбранных осей координат, реакцию шарнирно-подвижной опоры на катках В направляем перпендикулярно плоскости качения катков).
(реакцию шарнирно неподвижной опоры B изображаем двумя составляющими, направленными вдоль выбранных осей координат, реакцию шарнирно-подвижной опоры на катках В направляем перпендикулярно плоскости качения катков).
2. Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил на оси координат равнялись нулю и чтобы сумма моментов всех сил относительно точки В тоже равнялась нулю.
Составляем указанные уравнения равновесия:
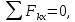
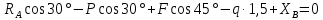 ; (1)
; (1)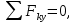
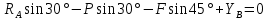 ; (2)
; (2)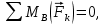
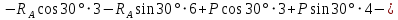
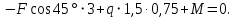 (3)
(3)Решаем систему уравнений (1)–(3) и находим реакции.
Из уравнения (3) находим
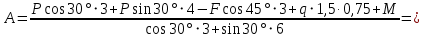
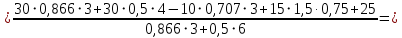
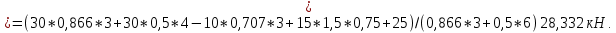
Из уравнения (1) получаем
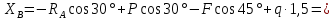
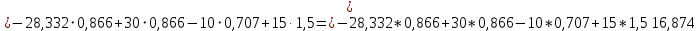 кН.
кН.Из уравнения (2) будем иметь
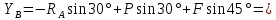
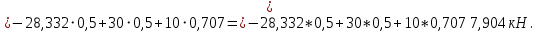
Рис.1. Расчетная схема к задаче С1
Ответ:
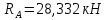 ;
; 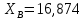 кН;
кН; 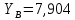 кН.
кН.Задача С2. Определение реакций опор твёрдого тела
(пространственная система сил)
Определить значение силы P и реакции опор твёрдого тела, изображённого на рис. С2.0–С2.9. Исходные данные для расчёта представлены в таблице С2.
Исходные данные:
Таблица С2
| Номер условия | 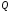 , ,кН |  , ,кН | 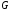 , ,кН |  , ,м | 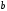 , ,м |  , ,м | 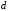 , ,м |  , ,м |  , ,м |  , ,град |
| 2 | 10 | 5 | 4 | 1 | 1,5 | 1,5 | 0,5 | 2 | 1 | 60 |
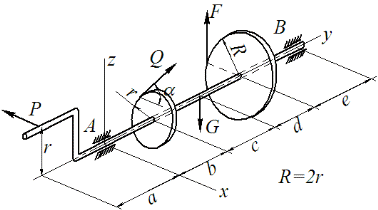
Рис. С2.2
Решение
Выполняем расчетную схему вала согласно исходным данным (рис.2).
Рассмотрим равновесие вала. На вал действуют заданные силы
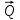 ,
, 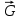 ,
,  , искомая сила
, искомая сила  , а также реакции связей (рис.2). Реакцию радиального подшипника А разложим на две составляющие
, а также реакции связей (рис.2). Реакцию радиального подшипника А разложим на две составляющие 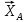 ,
, 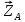 , а радиального подшипника В – на две составляющие
, а радиального подшипника В – на две составляющие  ,
, 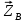 .
.Из указанных сил – пять неизвестных. Для их определения составим пять уравнений равновесия.
Уравнения моментов относительно координатных осей:
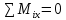 ;
; 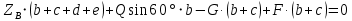 ; (1)
; (1)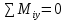 ;
; 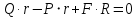 ; (2)
; (2)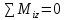 ;
; 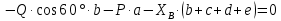 . (3)
. (3)Из уравнения (2) определяем усилие
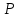 , а затем из уравнений (1) и (3) находим
, а затем из уравнений (1) и (3) находим 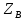 и
и 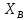 . В результате получим
. В результате получим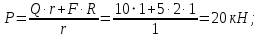
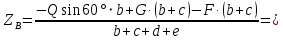
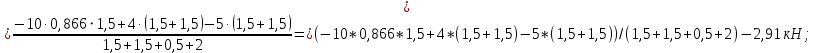
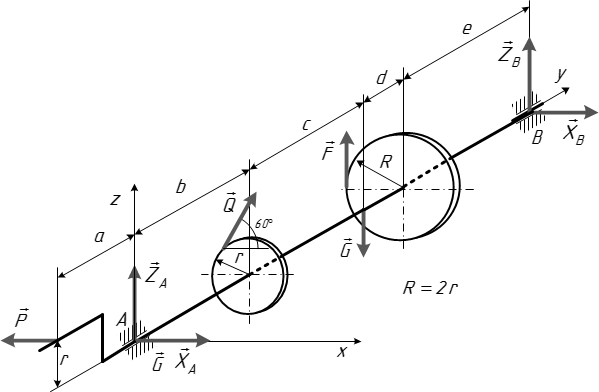
Рис. 2. Расчетная схема вала
Далее составим уравнения проекций сил на оси координат:
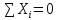 ;
; 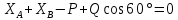 ; (4)
; (4)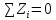 ;
; 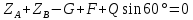 . (5)
. (5)Из этих уравнений находим
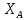 и
и 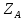 :
: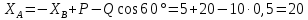 кН;
кН;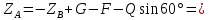
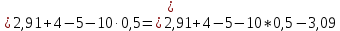 кН.
кН.Знак минус указывает на то, что действительные направления реакций
 ,
,  и
и  противоположны направлениям, принятым на рис.2.
противоположны направлениям, принятым на рис.2.Ответ:
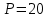 кН;
кН; 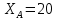 кН;
кН; 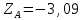 кН;
кН;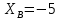 кН;
кН; 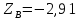 кН
кНЗадача К1. Кинематика плоских механизмов
Плоский кривошипно-шатунный механизм связан с системой зубчатых колес, насаженных на неподвижные оси, которые приводятся в движение ведущим звеном (зубчатая рейка – схема К1.0; рукоятка – схема К1.1; груз на нити – схема К1.2 и т. д.). Рукоятка О1А и кривошип О2С жестко связаны с соответствующими колесами. Длина кривошипа О2С = L1, шатуна CD = L2.
Схемы механизмов приведены на рис. К1.0–К1.9, а размеры и уравнения движения точки А ведущего звена S = f(t) – в таблице К2. В начальный момент направление кривошипа совпадает с осью x.
Требуется определить в заданном положении механизма угловые скорости колес ω1 и ω2, уравнение вращения кривошипа
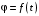 и время t1, соответствующее заданному положению кривошипа, скорость
и время t1, соответствующее заданному положению кривошипа, скорость 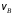 и ускорение
и ускорение
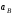 точки В колеса, скорость
точки В колеса, скорость 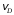 ,
, 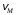 и ускорение
и ускорение 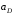 ,
, 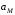 точек D и М шатуна соответственно, угловую скорость
точек D и М шатуна соответственно, угловую скорость 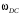 и угловое ускорение
и угловое ускорение 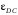 шатуна.
шатуна.Исходные данные:
Таблица К1
| Вариант | Размеры звеньев и углы в заданном положении механизма | Закон движения точки А ведущего звена 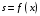 | ||||||
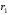 , м , м | 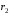 , м , м | 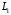 , м , м | 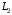 , м , м | 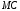 , м , м | 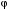 , ,град |  , ,град | ||
| 2 | 0,2 | 0,15 | 0,35 | 0,3 | 0,2 | 90 | 60 | 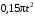 |
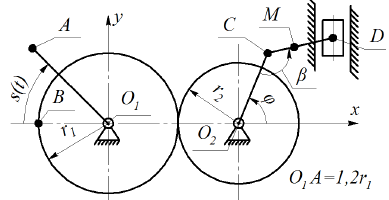
Рис. К1.2
Решение
1. Угловая скорость колеса 1 равна
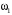 , а линейная скорость точки В, как точки, принадлежащей колесу 1, равна
, а линейная скорость точки В, как точки, принадлежащей колесу 1, равна 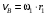 . С другой стороны, считая рукоятку жестко соединенной с колесом 1, имеем
. С другой стороны, считая рукоятку жестко соединенной с колесом 1, имеем 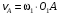 , (1)
, (1)где
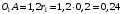 м – заданная длина рукоятки.
м – заданная длина рукоятки.В свою очередь, уравнение движения точки А задано естественным способом: