Файл: Контрольная работа Вариант 22 Задачи С1, С2, К1, К2, Д1, Д2 Задача равновесие произвольной плоской системы сил.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 49
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
и абсолютного ускорения точки 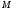
В соответствии с правилом векторного умножения вектор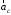 направлен так, как показано на рис.4.
направлен так, как показано на рис.4.
3. Перепишем уравнение (1) в развернутом виде
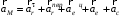 (2)
(2)
и определим модуль абсолютного ускорения точки М, используя способ проекций.
Проецируя уравнение (2) на оси координат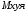 , находим
, находим
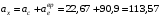 см/с2;
см/с2;
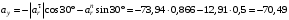 см/с2;
см/с2;
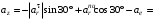
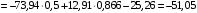 см/с2.
см/с2.
Далее вычисляем абсолютное ускорение точки М:
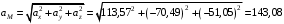 см/с2.
см/с2.
Ответ: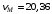 см/с;
см/с; 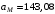 см/с2.
см/с2.
Задача Д1. Применение теоремы об изменении кинетической энергии
к исследованию движения механической системы
Механическая система состоит из трёх движущихся тел (рис. Д1.0–Д1.9), соединенных нерастяжимыми нитями, параллельными соответствующим плоскостям. Неподвижные и подвижные блоки одного радиуса считать однородными сплошными цилиндрами радиуса R; ступенчатые блоки (подвижные и неподвижные) с радиусами ступеней R и r имеют радиус инерции ρ. К одному из тел прикреплена пружина жёсткости c. Под действием силы F = F(s), зависящей от перемещения s точки её приложения, система приходит в движение из состояния покоя; деформация пружины в начальный момент времени равна нулю. При движении на шкив 2 действует момент сил сопротивления MC= MC(φ), зависящий от угла φ поворота шкива 2.
Определить значение искомой величины в момент времени, когда центр масс тела 1 переместиться на заданную величину s1. Искомая величина указана в столбце «Найти» таблицы, где обозначено:
υ1, υC3 – скорости груза 1 и скорость центра масс катка 3 соответственно; ω2, ω3 и – угловые скорости тел 2 и 3.
Все катки, включая катки, обмотанные нитями, движутся по плоскостям без скольжения. Данные для численных расчётов приведены в таблице Д1.
Исходные данные:
Таблица Д1
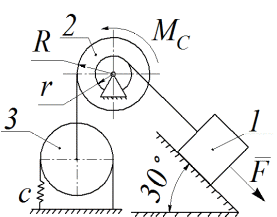
Рис. Д1.2
Решение
Применим теорему об изменении кинетической энергии системы в интегральной форме:
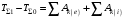 , (1)
, (1)
где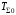 и
и 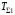 –кинетическая энергия системы в начальном и конечном положениях;
–кинетическая энергия системы в начальном и конечном положениях; 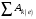 – сумма работ внешних сил, приложенных к системе, на перемещении системы из начального положения в конечное;
– сумма работ внешних сил, приложенных к системе, на перемещении системы из начального положения в конечное; 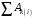
– сумма работ внутренних сил системы на том же перемещении.
Для рассматриваемой системы, состоящих из абсолютно твердых тел, соединенных нерастяжимыми нитями и стержнями,
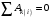 .
.
Так как в начальном положении система находится в покое, то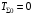 .
.
Следовательно, уравнение (1) принимает вид
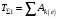 . (2)
. (2)
Начинаем решение задачи с определения кинетической энергии системы
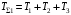 , (3)
, (3)
где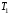 – кинетическая энергия поступательно движущегося груза 1;
– кинетическая энергия поступательно движущегося груза 1;
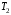 – кинетическая энергия блока 2, вращающегося вокруг неподвижной оси;
– кинетическая энергия блока 2, вращающегося вокруг неподвижной оси;
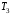 – кинетическая энергия блока 3, совершающего плоское движение.
– кинетическая энергия блока 3, совершающего плоское движение.
Учитывая вид движения каждого из 3-х тел системы, определим их кинетическую энергию:
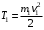 , (4)
, (4)
где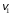 – скорость тела 1;
– скорость тела 1;
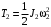 , (5)
, (5)
где – угловая скорость вращения блока 2;
– угловая скорость вращения блока 2; 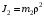 – момент инерции ступенчатого блока 2 относительно оси вращения;
– момент инерции ступенчатого блока 2 относительно оси вращения;
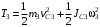 , (6)
, (6)
где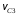 – скорость центра масс
– скорость центра масс 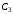 блока 3;
блока 3;
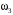 – угловая скорость вращения блока 3;
– угловая скорость вращения блока 3;
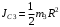 – момент инерции однородного блока 3 относительно оси, проходящей через его центр масс.
– момент инерции однородного блока 3 относительно оси, проходящей через его центр масс.
Все скорости, входящие в формулы (4)–(6), необходимо выразить через искомую
 . Для этого учтём, что точка Р – мгновенный центр скоростей блока 3.
. Для этого учтём, что точка Р – мгновенный центр скоростей блока 3.
Скорость груза 1 равна скорости точки А блока 2, т.е.
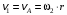 .
.
Скорость точки блока 3 равна скорости точки В блока 2, т.е.
блока 3 равна скорости точки В блока 2, т.е.
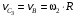 .
.
Угловая скорость блока 3 равна
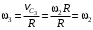 .
.
Подставляя выражения для ,
, 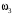 и
и  в (4)–(6), а затем в (3), получаем
в (4)–(6), а затем в (3), получаем
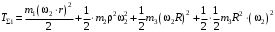
или
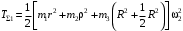 .
.
Выполняя вычисления, получим
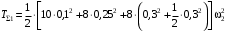
или окончательно
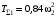 . (7)
. (7)
Далее определяем работу всех внешних сил, приложенных к системе на перемещениях точек их приложения, выраженных через s1. К системе приложены следующие внешние силы: силы тяжести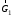 ,
, 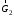 ,
, 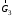 , реакции опор
, реакции опор 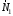 ,
, 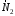 , сила натяжения нити
, сила натяжения нити 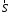 , пара сил, образующая момент сопротивления
, пара сил, образующая момент сопротивления 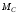 , сила
, сила 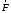 , приложенная к грузу 1 и сила упругости пружины
, приложенная к грузу 1 и сила упругости пружины 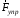 . Работа сил
. Работа сил 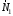 ,
, 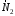 ,
, 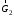 и
и 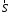 равна нулю, так как сила
равна нулю, так как сила 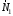 перпендикулярна перемещению точки её приложения, силы
перпендикулярна перемещению точки её приложения, силы 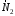
и приложены в неподвижной точке, а точкой приложения силы
приложены в неподвижной точке, а точкой приложения силы  является мгновенный центр скоростей (точка Р, неподвижная в данный момент времени). Работы остальных сил определяются следующим образом:
является мгновенный центр скоростей (точка Р, неподвижная в данный момент времени). Работы остальных сил определяются следующим образом:
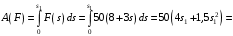
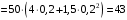 Дж. (8)
Дж. (8)
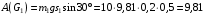 Дж. (9)
Дж. (9)
Для определения перемещения центра масс катка 3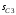 выразим скорость
выразим скорость  через
через  :
:
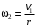 ;
; 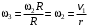 ;
;
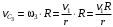 .
.
Тогда
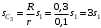 .
.
Тогда работа силы тяжести тела 3 будет равна
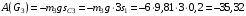 Дж. (10)
Дж. (10)
Работа момента сопротивления определяется по формуле
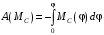 ,
,
где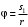 – угол поворота блока 2, соответствующий перемещению груза 1 на величину
– угол поворота блока 2, соответствующий перемещению груза 1 на величину  . Тогда
. Тогда
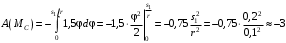 Дж. (11)
Дж. (11)
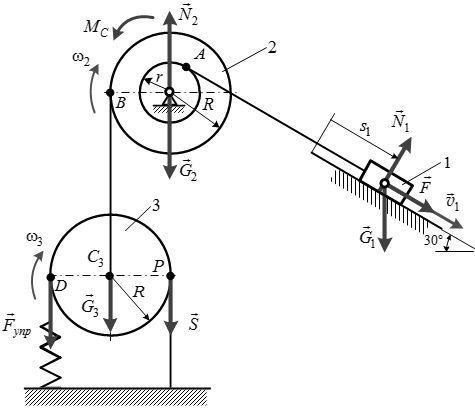
Рис.5. Расчетная схема к задаче Д1
Работа силы упругости пружины определяется как
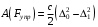 ,
,
где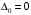 – начальная деформация пружины по условию задачи;
– начальная деформация пружины по условию задачи;
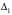 – конечная деформация пружины, равная перемещению точки
– конечная деформация пружины, равная перемещению точки  , т.е.
, т.е. 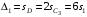 .
.
Тогда получим
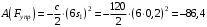 Дж. (12)
Дж. (12)
Суммируя (8)–(12), получаем
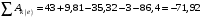 Дж. (13)
Дж. (13)
Поскольку получили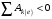
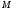
В соответствии с правилом векторного умножения вектор
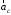 направлен так, как показано на рис.4.
направлен так, как показано на рис.4.3. Перепишем уравнение (1) в развернутом виде
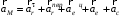 (2)
(2)и определим модуль абсолютного ускорения точки М, используя способ проекций.
Проецируя уравнение (2) на оси координат
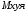 , находим
, находим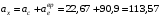 см/с2;
см/с2;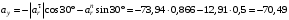 см/с2;
см/с2;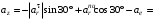
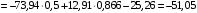 см/с2.
см/с2.Далее вычисляем абсолютное ускорение точки М:
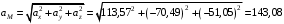 см/с2.
см/с2.Ответ:
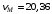 см/с;
см/с; 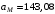 см/с2.
см/с2. Задача Д1. Применение теоремы об изменении кинетической энергии
к исследованию движения механической системы
Механическая система состоит из трёх движущихся тел (рис. Д1.0–Д1.9), соединенных нерастяжимыми нитями, параллельными соответствующим плоскостям. Неподвижные и подвижные блоки одного радиуса считать однородными сплошными цилиндрами радиуса R; ступенчатые блоки (подвижные и неподвижные) с радиусами ступеней R и r имеют радиус инерции ρ. К одному из тел прикреплена пружина жёсткости c. Под действием силы F = F(s), зависящей от перемещения s точки её приложения, система приходит в движение из состояния покоя; деформация пружины в начальный момент времени равна нулю. При движении на шкив 2 действует момент сил сопротивления MC= MC(φ), зависящий от угла φ поворота шкива 2.
Определить значение искомой величины в момент времени, когда центр масс тела 1 переместиться на заданную величину s1. Искомая величина указана в столбце «Найти» таблицы, где обозначено:
υ1, υC3 – скорости груза 1 и скорость центра масс катка 3 соответственно; ω2, ω3 и – угловые скорости тел 2 и 3.
Все катки, включая катки, обмотанные нитями, движутся по плоскостям без скольжения. Данные для численных расчётов приведены в таблице Д1.
Исходные данные:
Таблица Д1
| Номер условия | 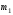 , ,кг | 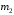 , ,кг | 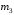 , ,кг |  , ,Н/м | 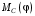 Н·м Н·м | 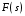 , ,Н | 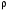 , ,м | 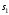 , ,м |  , ,м |  , ,м | Найти |
| 2 | 10 | 8 | 6 | 120 | 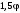 | 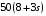 | 0,25 | 0,2 | 0,3 | 0,1 | 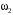 |
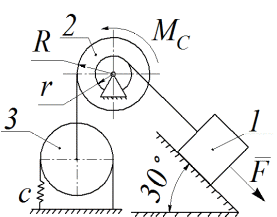
Рис. Д1.2
Решение
Применим теорему об изменении кинетической энергии системы в интегральной форме:
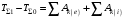 , (1)
, (1)где
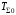 и
и 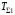 –кинетическая энергия системы в начальном и конечном положениях;
–кинетическая энергия системы в начальном и конечном положениях; 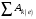 – сумма работ внешних сил, приложенных к системе, на перемещении системы из начального положения в конечное;
– сумма работ внешних сил, приложенных к системе, на перемещении системы из начального положения в конечное; 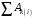
– сумма работ внутренних сил системы на том же перемещении.
Для рассматриваемой системы, состоящих из абсолютно твердых тел, соединенных нерастяжимыми нитями и стержнями,
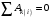 .
.Так как в начальном положении система находится в покое, то
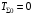 .
.Следовательно, уравнение (1) принимает вид
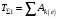 . (2)
. (2)Начинаем решение задачи с определения кинетической энергии системы
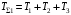 , (3)
, (3)где
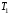 – кинетическая энергия поступательно движущегося груза 1;
– кинетическая энергия поступательно движущегося груза 1;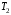 – кинетическая энергия блока 2, вращающегося вокруг неподвижной оси;
– кинетическая энергия блока 2, вращающегося вокруг неподвижной оси;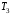 – кинетическая энергия блока 3, совершающего плоское движение.
– кинетическая энергия блока 3, совершающего плоское движение.Учитывая вид движения каждого из 3-х тел системы, определим их кинетическую энергию:
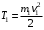 , (4)
, (4)где
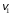 – скорость тела 1;
– скорость тела 1;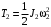 , (5)
, (5)где
 – угловая скорость вращения блока 2;
– угловая скорость вращения блока 2; 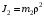 – момент инерции ступенчатого блока 2 относительно оси вращения;
– момент инерции ступенчатого блока 2 относительно оси вращения;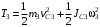 , (6)
, (6)где
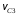 – скорость центра масс
– скорость центра масс 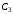 блока 3;
блока 3;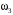 – угловая скорость вращения блока 3;
– угловая скорость вращения блока 3;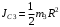 – момент инерции однородного блока 3 относительно оси, проходящей через его центр масс.
– момент инерции однородного блока 3 относительно оси, проходящей через его центр масс.Все скорости, входящие в формулы (4)–(6), необходимо выразить через искомую
 . Для этого учтём, что точка Р – мгновенный центр скоростей блока 3.
. Для этого учтём, что точка Р – мгновенный центр скоростей блока 3. Скорость груза 1 равна скорости точки А блока 2, т.е.
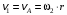 .
.Скорость точки
 блока 3 равна скорости точки В блока 2, т.е.
блока 3 равна скорости точки В блока 2, т.е.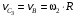 .
.Угловая скорость блока 3 равна
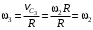 .
.Подставляя выражения для
 ,
, 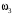 и
и  в (4)–(6), а затем в (3), получаем
в (4)–(6), а затем в (3), получаем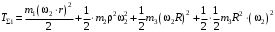
или
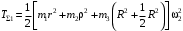 .
.Выполняя вычисления, получим
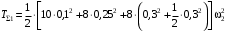
или окончательно
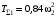 . (7)
. (7)Далее определяем работу всех внешних сил, приложенных к системе на перемещениях точек их приложения, выраженных через s1. К системе приложены следующие внешние силы: силы тяжести
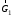 ,
, 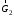 ,
, 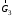 , реакции опор
, реакции опор 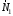 ,
, 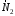 , сила натяжения нити
, сила натяжения нити 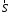 , пара сил, образующая момент сопротивления
, пара сил, образующая момент сопротивления 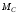 , сила
, сила 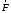 , приложенная к грузу 1 и сила упругости пружины
, приложенная к грузу 1 и сила упругости пружины 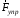 . Работа сил
. Работа сил 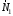 ,
, 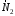 ,
, 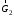 и
и 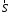 равна нулю, так как сила
равна нулю, так как сила 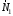 перпендикулярна перемещению точки её приложения, силы
перпендикулярна перемещению точки её приложения, силы 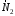
и
 приложены в неподвижной точке, а точкой приложения силы
приложены в неподвижной точке, а точкой приложения силы  является мгновенный центр скоростей (точка Р, неподвижная в данный момент времени). Работы остальных сил определяются следующим образом:
является мгновенный центр скоростей (точка Р, неподвижная в данный момент времени). Работы остальных сил определяются следующим образом: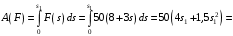
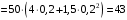 Дж. (8)
Дж. (8)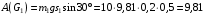 Дж. (9)
Дж. (9)Для определения перемещения центра масс катка 3
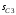 выразим скорость
выразим скорость  через
через  :
: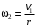 ;
; 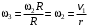 ;
;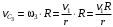 .
.Тогда
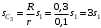 .
.Тогда работа силы тяжести тела 3 будет равна
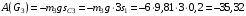 Дж. (10)
Дж. (10)Работа момента сопротивления определяется по формуле
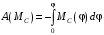 ,
,где
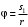 – угол поворота блока 2, соответствующий перемещению груза 1 на величину
– угол поворота блока 2, соответствующий перемещению груза 1 на величину  . Тогда
. Тогда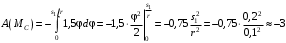 Дж. (11)
Дж. (11)
Рис.5. Расчетная схема к задаче Д1
Работа силы упругости пружины определяется как
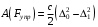 ,
,где
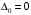 – начальная деформация пружины по условию задачи;
– начальная деформация пружины по условию задачи;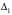 – конечная деформация пружины, равная перемещению точки
– конечная деформация пружины, равная перемещению точки  , т.е.
, т.е. 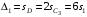 .
.Тогда получим
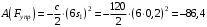 Дж. (12)
Дж. (12)Суммируя (8)–(12), получаем
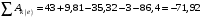 Дж. (13)
Дж. (13)Поскольку получили