Файл: Контрольная работа Вариант 22 Задачи С1, С2, К1, К2, Д1, Д2 Задача равновесие произвольной плоской системы сил.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 47
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, то это означает, что приложенных сил недостаточно для преодоления сил сопротивления и механическая система находится в покое, т.е. 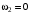 .
.
Изменим исходные данные и примем значение силы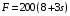 .
.
Тогда
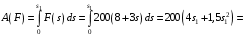
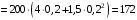 Дж.
Дж.
Тогда
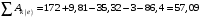 Дж. (14)
Дж. (14)
Приравнивая выражения (7) и (14) на основании (2), получим
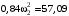 ,
,
откуда находим искомую скорость
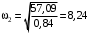 рад/с.
рад/с.
Ответ: 1)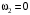 при заданных исходных данных;
при заданных исходных данных;
2)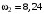 рад/с при измененных исходных данных..
рад/с при измененных исходных данных..
Задача Д2. Применение принципа Даламбера к определению
реакций связей
Вертикальный вал АК (рис. Д2.0–Д2.9), вращающийся с постоянной угловой скоростью ω = 10 c-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в таблице Д2, в столбце 2. При этом АВ = ВD = DЕ = ЕК = а. К валу жестко прикреплены однородный стержень 1 длиной l1= 0,6 м, имеющий массу m1 =3 кг, и невесомый стержень 2 длиной l2 = 0,4 м и с точечной массой m2 = 5 кг на конце. Оба стержня лежат в одной плоскости. Точки крепления стержней к валу указаны в таблице в столбцах 3 и 4, а углы α и β – в столбцах 5 и 6.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять a = 0,4 м.
Исходные данные:
Таблица Д2
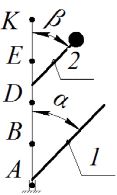
Рис. Д2.2
Решение
1. Изображаем (с учетом заданных углов) вал и прикрепленные к нему в точках D и Kстержни (рис.6). Силы тяжести стержня 1 и груза 2 соответственно равны
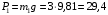 Н;
Н;
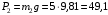 Н. (1)
Н. (1)
2. Для определения искомых реакций рассмотрим движение заданной механической системы и применим принцип Даламбера. Проведем вращающиеся вместе с валом координатные оси
так, чтобы стержень лежал в плоскости , и изобразим действующие на систему силы: активные силы – силы тяжести
, и изобразим действующие на систему силы: активные силы – силы тяжести  ,
,  и реакции связей – составляющие реакции подпятника
и реакции связей – составляющие реакции подпятника  ,
,  и реакцию цилиндрического подшипника
и реакцию цилиндрического подшипника 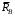 .
.
Согласно принципу Даламбера, присоединим к эти силам силы инерции груза 2 и элементов однородного стержня 1.
Так как вал вращается равномерно, то элементы стержня 1 имеют только нормальные ускорения , направленные к оси вращения, а численно
, направленные к оси вращения, а численно  , где
, где  – расстояния элементов от оси вращения. тогда силы инерции
– расстояния элементов от оси вращения. тогда силы инерции  будут направлены от оси вращения, а численно
будут направлены от оси вращения, а численно
 ,
,
где – масса элемента.
– масса элемента.
Так как все пропорциональны
пропорциональны  , то эпюры этих параллельных сил инерции стержня образуют для стержня 1 треугольник (рис.6).
, то эпюры этих параллельных сил инерции стержня образуют для стержня 1 треугольник (рис.6).
Полученную систему параллельных сил инерции заменим ее равнодействующей, равной главному вектору этих сил. Так как момент главного вектора сил инерции любого тела имеет значение
, где – масса тела,
– масса тела,  – ускорение его центра масс, то для стержня 1 и груза 2 получим
– ускорение его центра масс, то для стержня 1 и груза 2 получим
 ,
,  . (2)
. (2)
Ускорение центров масс стержня 1 и груза 2 равны:
 ,
,  , (3)
, (3)
где – расстояния центров масс от оси вращения:
– расстояния центров масс от оси вращения:
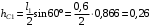 м;
м;
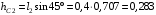 м. (4)
м. (4)
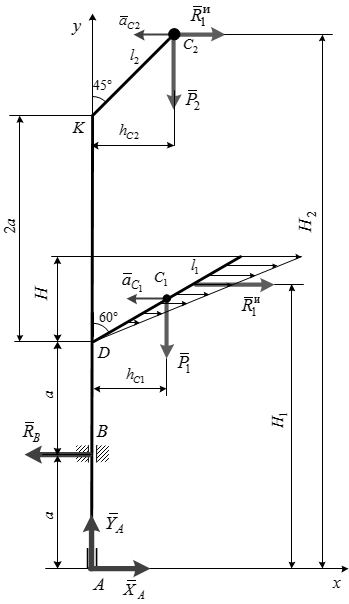
Рис.6. Расчетная схема к задаче Д2
Подставив в (2) значения (3) и учтя (4), получим числовые значения и
и  :
:
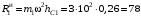 Н;
Н;
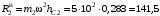 Н. (5)
Н. (5)
При этом линия действия равнодействующей пройдет через центр тяжести соответствующей эпюры силы инерции – на расстоянии
пройдет через центр тяжести соответствующей эпюры силы инерции – на расстоянии  от вершины треугольника D, где
от вершины треугольника D, где 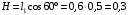 м.
м.
3. Согласно принципу Даламбера, приложенные внешние силы (активные и реакции связей) и силы инерции образуют уравновешенную систему сил. Составим для этой плоской системы сил три уравнения равновесия. Получим
 ;
; 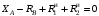
; (6)
 ;
;  ; (7)
; (7)
 ;
; 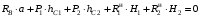 , (8)
, (8)
где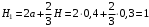 м;
м;
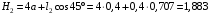 м.
м.
Из уравнения (8) находим
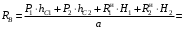
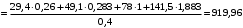 Н.
Н.
Из уравнения (6) имеем
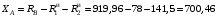 Н.
Н.
Из уравнения (7) получаем
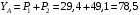 Н.
Н.
Результирующая реакция подпятника
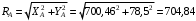 Н.
Н.
Ответ: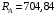 Н;
Н; 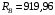 Н.
Н.
Список использованной литературы
1. Мустафаев Ю.К., Червинский В.П. Теоретическая механика. Методические указания к выполнению контрольных работ. Самара, СамГУПС, 2020.
2. Яблонский А.А., Никифорова В.М. Курс теоретической механики. М.: Интеграл–Пресс, 2006.
3. Тарг С.М. Краткий курс теоретической механики. М.: Высшая школа, 2008.
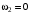 .
.Изменим исходные данные и примем значение силы
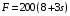 .
.Тогда
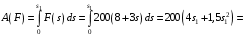
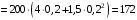 Дж.
Дж.Тогда
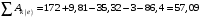 Дж. (14)
Дж. (14)Приравнивая выражения (7) и (14) на основании (2), получим
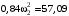 ,
,откуда находим искомую скорость

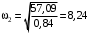 рад/с.
рад/с.Ответ: 1)
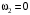 при заданных исходных данных;
при заданных исходных данных;2)
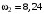 рад/с при измененных исходных данных..
рад/с при измененных исходных данных..Задача Д2. Применение принципа Даламбера к определению
реакций связей
Вертикальный вал АК (рис. Д2.0–Д2.9), вращающийся с постоянной угловой скоростью ω = 10 c-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в таблице Д2, в столбце 2. При этом АВ = ВD = DЕ = ЕК = а. К валу жестко прикреплены однородный стержень 1 длиной l1= 0,6 м, имеющий массу m1 =3 кг, и невесомый стержень 2 длиной l2 = 0,4 м и с точечной массой m2 = 5 кг на конце. Оба стержня лежат в одной плоскости. Точки крепления стержней к валу указаны в таблице в столбцах 3 и 4, а углы α и β – в столбцах 5 и 6.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять a = 0,4 м.
Исходные данные:
Таблица Д2
| Номер условия | Подшипник в точке | Крепление | α, град | , град | |
| стержня 1 в точке | стержня 2 в точке | ||||
| 2 | B | D | K | 60 | 45 |
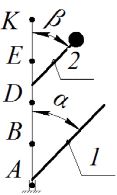
Рис. Д2.2
Решение
1. Изображаем (с учетом заданных углов) вал и прикрепленные к нему в точках D и Kстержни (рис.6). Силы тяжести стержня 1 и груза 2 соответственно равны
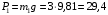 Н;
Н;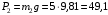 Н. (1)
Н. (1)2. Для определения искомых реакций рассмотрим движение заданной механической системы и применим принцип Даламбера. Проведем вращающиеся вместе с валом координатные оси
так, чтобы стержень лежал в плоскости
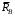 .
.Согласно принципу Даламбера, присоединим к эти силам силы инерции груза 2 и элементов однородного стержня 1.
Так как вал вращается равномерно, то элементы стержня 1 имеют только нормальные ускорения
где
Так как все
Полученную систему параллельных сил инерции заменим ее равнодействующей, равной главному вектору этих сил. Так как момент главного вектора сил инерции любого тела имеет значение
, где
Ускорение центров масс стержня 1 и груза 2 равны:
где
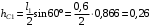 м;
м;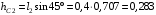 м. (4)
м. (4)
Рис.6. Расчетная схема к задаче Д2
Подставив в (2) значения (3) и учтя (4), получим числовые значения
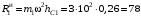 Н;
Н;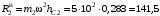 Н. (5)
Н. (5)При этом линия действия равнодействующей
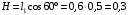 м.
м.3. Согласно принципу Даламбера, приложенные внешние силы (активные и реакции связей) и силы инерции образуют уравновешенную систему сил. Составим для этой плоской системы сил три уравнения равновесия. Получим
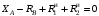
; (6)
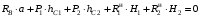 , (8)
, (8)где
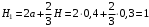 м;
м;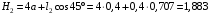 м.
м.Из уравнения (8) находим
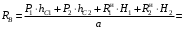
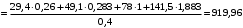 Н.
Н.Из уравнения (6) имеем
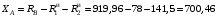 Н.
Н.Из уравнения (7) получаем
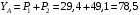 Н.
Н.Результирующая реакция подпятника
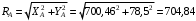 Н.
Н.Ответ:
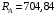 Н;
Н; 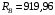 Н.
Н.Список использованной литературы
1. Мустафаев Ю.К., Червинский В.П. Теоретическая механика. Методические указания к выполнению контрольных работ. Самара, СамГУПС, 2020.
2. Яблонский А.А., Никифорова В.М. Курс теоретической механики. М.: Интеграл–Пресс, 2006.
3. Тарг С.М. Краткий курс теоретической механики. М.: Высшая школа, 2008.