Файл: Контрольная работа Вариант 22 Задачи С1, С2, К1, К2, Д1, Д2 Задача равновесие произвольной плоской системы сил.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 48
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
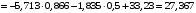 м/с2.
м/с2.Находим модуль ускорения точки М
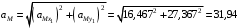 м/с2.
м/с2.Ответ:
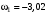 рад/с;
рад/с; 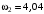 рад/с;
рад/с; 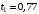 с;
с; 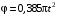 (рад);
(рад);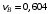 м/с;
м/с; 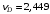 м/с;
м/с; 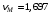 м/с;
м/с; 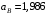 м/с2;
м/с2; 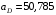 м/с2;
м/с2; 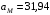 м/с2;
м/с2; 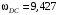 рад/с;
рад/с; 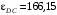 рад/с2.
рад/с2.Задача К2. Сложное движение точки
По заданному уравнению вращения
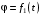 тела А и уравнению движения
тела А и уравнению движения 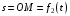 точки М относительно тела А определить абсолютную скорость и абсолютное ускорение точки М в момент времени
точки М относительно тела А определить абсолютную скорость и абсолютное ускорение точки М в момент времени  . Схема к задаче и исходные данные к ней определяются в соответствии с шифром по рис. К2.0–К2.9 и таблице К2. Точка М показана в направлении положительного отсчета координаты s. Положительное направление отсчета угла
. Схема к задаче и исходные данные к ней определяются в соответствии с шифром по рис. К2.0–К2.9 и таблице К2. Точка М показана в направлении положительного отсчета координаты s. Положительное направление отсчета угла  указано стрелкой.
указано стрелкой.Исходные данные:
Таблица К2
| Номер условия | Уравнение вращения тела А 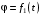 , рад , рад | Уравнение относительного движения точки 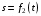 , см , см |  , с , с | 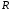 , см , см |
| 2 | 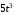 | 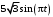 | 1/3 | 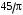 |
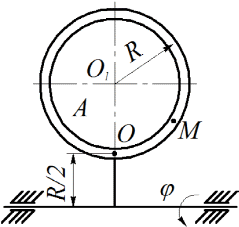
Рис. К2.3
Решение
Точка М совершает сложное движение. Относительным движением точки М является движение относительно тела А, переносным – вращение тела А вокруг горизонтальной оси BC. Свяжем с телом А подвижную систему координат, направив ось xперпендикулярно плоскости рисунка на нас (рис. 4).
Положение точки М в момент времени
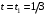 c определим углом α, на который повернется радиус, проведенный из центра О1 в точку М, за время движения.
c определим углом α, на который повернется радиус, проведенный из центра О1 в точку М, за время движения.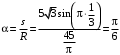 рад
рад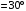 .
.1. Абсолютная скорость точки М равна геометрической сумме относительной и переносной скоростей:
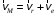 .
.Движение точки М относительно тела А задано естественным способом, поэтому относительную скорость определяем из формулы
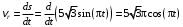
и при
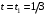 с получим
с получим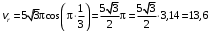 см/с.
см/с.Так как знак скорости положителен, то вектор
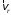 направлен в сторону возрастания координаты s (положительное направлению отсчета) по касательной к траектории, т. е. перпендикулярно радиусу R в точке М.
направлен в сторону возрастания координаты s (положительное направлению отсчета) по касательной к траектории, т. е. перпендикулярно радиусу R в точке М. Переносная скорость
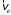 точки М равна скорости той точки тела А, с которой она совпадает в данный момент. Тело А совершает вращательное движение вокруг оси BC, поэтому по модулю
точки М равна скорости той точки тела А, с которой она совпадает в данный момент. Тело А совершает вращательное движение вокруг оси BC, поэтому по модулю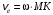 ,
,где
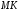 – расстояние от точки М до оси
– расстояние от точки М до оси 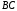 ;
; 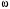 – угловая скорость переносного вращательного движения.
– угловая скорость переносного вращательного движения.Так как уравнение вращательного движения φ = f1(t) задано, то находим
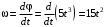
и при
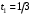 с получаем
с получаем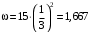
рад/с.
Знак плюс указывает на то, что в момент времени
 c тело А вращается в направлении, совпадающим с положительным отсчетом угла φ (рис. 4).
c тело А вращается в направлении, совпадающим с положительным отсчетом угла φ (рис. 4).При
 с расстояние
с расстояние  равно
равно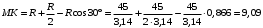 см.
см.Тогда величина переносной скорости будет равна
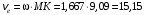 см/с.
см/с.Вектор
 направлен перпендикулярно
направлен перпендикулярно  в сторону вращения тела. Так как в данном случае векторы
в сторону вращения тела. Так как в данном случае векторы  и
и  оказались взаимно перпендикулярными, то модуль абсолютной скорости точки М
оказались взаимно перпендикулярными, то модуль абсолютной скорости точки М 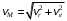
и при
 с получим
с получим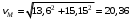 см/с.
см/с.2. Определение абсолютного ускорения точки М.
Согласно теореме сложения ускорений (теорема Кориолиса) абсолютное ускорение точки в случае переносного вращательного движения равно геометрической сумме относительного, переносного и кориолисова ускорений:
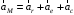 . (1)
. (1)При естественном способе задания относительного движения относительное ускорение точки определяется выражением:
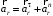 .
.Величины касательной
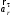 и нормальной
и нормальной 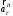 составляющих равны:
составляющих равны: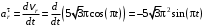 ;
;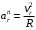 .
.При
 с будем иметь
с будем иметь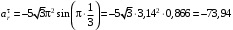 см/с2;
см/с2;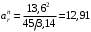 см/с2.
см/с2.Переносное ускорение
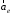
точки М также складывается из двух составляющих:
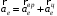 ,
,так как переносное движение является вращательным.
По модулю вращательная составляющая
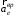 и центростремительная составляющая
и центростремительная составляющая 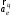 переносного ускорения определяются выражениями:
переносного ускорения определяются выражениями: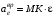 ,
, 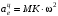 , (2)
, (2)где
 – угловое ускорение тела А.
– угловое ускорение тела А.По определению
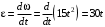 .
.При
 с
с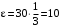 рад/с2.
рад/с2.Знаки
 и
и  положительны, поэтому одинаковы направления векторов
положительны, поэтому одинаковы направления векторов 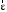 и
и  , а также
, а также 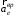 и
и  . Вектор
. Вектор 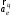 направлен к оси вращения, т. е. по линии МKк точке K.
направлен к оси вращения, т. е. по линии МKк точке K.Находим значения ускорений при
 с:
с: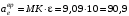 см/с2;
см/с2;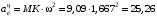 см/с2.
см/с2.Вектор кориолисова ускорения определяется по формуле:
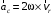 .
.Его модуль
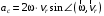 .
.Из рис.4 видно, что угол между векторами
 (направлен вдоль BC) и
(направлен вдоль BC) и  равен 30°, поэтому при
равен 30°, поэтому при  с
с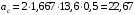 см/с2.
см/с2.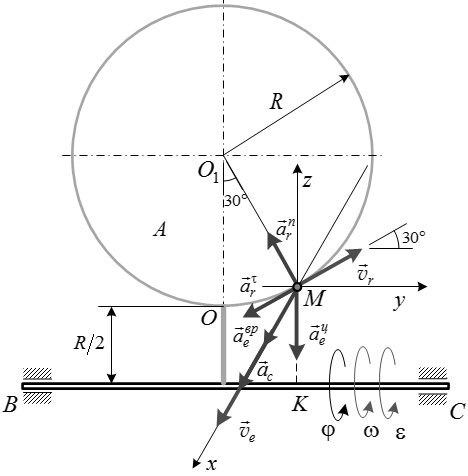
Рис.4. Расчетная схема для определения абсолютной скорости