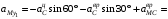Файл: Контрольная работа Вариант 22 Задачи С1, С2, К1, К2, Д1, Д2 Задача равновесие произвольной плоской системы сил.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 50
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
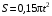 ,
,поэтому скорость точки А
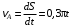 . (2)
. (2)Из (1) и (2) находим
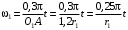 . (3)
. (3)Для определения угловой скорости
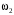 запишем выражение скорости точки касания колес K, рассматривая ее принадлежащей каждому из колес:
запишем выражение скорости точки касания колес K, рассматривая ее принадлежащей каждому из колес: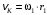 ,
, 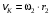 .
.Приравнивая скорости, находим
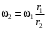
или с учетом (3)
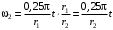 .
.Таким образом, значения угловых скоростей в общем виде будут следующими:
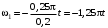 ;
;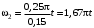 . (4)
. (4)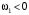 , поскольку колесо 1 вращается по часовой стрелке.
, поскольку колесо 1 вращается по часовой стрелке.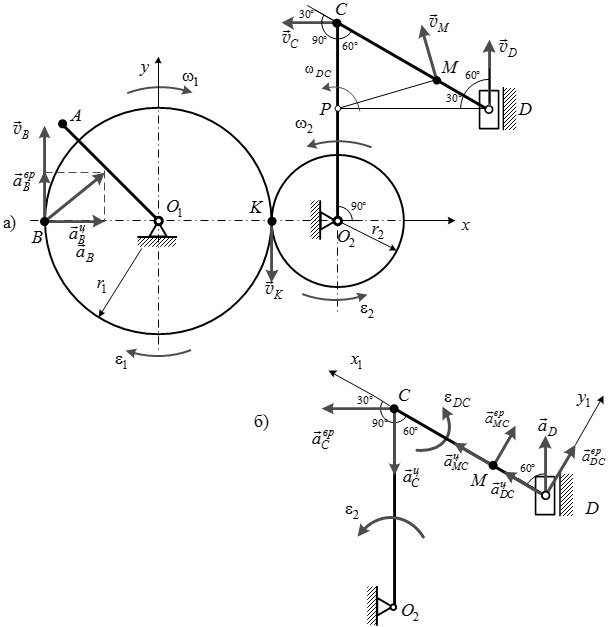
Рис.3. Расчетная схема механизма с параметрами движения точек и тел
Найдем уравнение движения кривошипа. Учитывая, что он жестко связан с колесом 2, запишем:
 ,
,откуда находим:
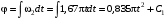 . (5)
. (5)Постоянную
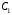 определяем по начальным условиям: при
определяем по начальным условиям: при 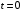 кривошип совпадал с направлением оси x, поэтому
кривошип совпадал с направлением оси x, поэтому 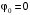 . Подставляя в (5), получим
. Подставляя в (5), получим 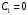 , и уравнение вращения кривошипа имеет вид
, и уравнение вращения кривошипа имеет вид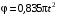 . (6)
. (6)Определим
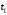 – время движения механизма в заданное положение, положив значение угла φ равным заданному, т.е.
– время движения механизма в заданное положение, положив значение угла φ равным заданному, т.е. 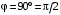 . Из уравнения (6) находим
. Из уравнения (6) находим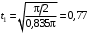 с,
с,т.к. время считается положительным.
Подставляя
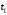
в (4), получим значения угловых скоростей в заданном положении:
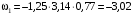 рад/с;
рад/с;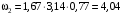 рад/с.
рад/с.Направление вращения колес показано стрелками на рис. 3, а.
3. Определим скорость и ускорение точки В колеса 1. По модулю скорость точки В колеса определяется выражением
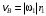
и для момента времени
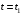 получим
получим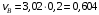 м/с.
м/с.Вектор скорости
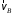 направлен в сторону вращения колеса перпендикулярно радиусу (рис. 3, а).
направлен в сторону вращения колеса перпендикулярно радиусу (рис. 3, а).Ускорение точки В равно векторной сумме вращательного и центростремительного ускорений:
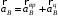 .
.Величины вращательной и центростремительной составляющих вектора
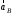 вычисляем по формулам:
вычисляем по формулам: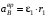 ;
;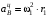 .
.Угловое ускорение
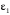 определим, дифференцируя по времени выражение для
определим, дифференцируя по времени выражение для  :
: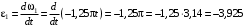 рад/с2.
рад/с2.Т.к. знаки
 и
и 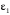 совпадают, то вращение колеса будет ускоренным, и направление вращательной составляющей ускорения совпадает с направлением скорости
совпадают, то вращение колеса будет ускоренным, и направление вращательной составляющей ускорения совпадает с направлением скорости  . Центростремительная составляющая ускорения всегда направлена к оси вращения (рис. 3, б).
. Центростремительная составляющая ускорения всегда направлена к оси вращения (рис. 3, б).Находим ускорения
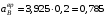 м/с2;
м/с2;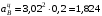 м/с2.
м/с2.Модуль полного ускорения точки В
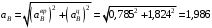 м/с2.
м/с2.4. Определение скорости точек
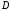 и
и  .
.Для определения скорости точки D воспользуемся теоремой о равенстве проекций скоростей двух точек плоской фигуры на прямую, соединяющую точки. Действительно, направление скоростей точек
D и С шатуна известны, кроме того, может быть найден и модуль скорости
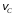 точки С. Если рассматривать точку С как точку, принадлежащую кривошипу О2С, жестко связанному с колесом 2, то по модулю величина
точки С. Если рассматривать точку С как точку, принадлежащую кривошипу О2С, жестко связанному с колесом 2, то по модулю величина 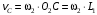 и для
и для 
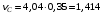 м/с.
м/с.Так как вектор скорости
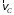 направлен перпендикулярно кривошипу О2С в сторону его поворота, то вектор
направлен перпендикулярно кривошипу О2С в сторону его поворота, то вектор 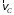 направлен под углом 30° к шатуну СD. Вектор скорости
направлен под углом 30° к шатуну СD. Вектор скорости 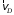 точки D направлен вдоль направляющих ползуна (рис. 3, а). Проецируя векторы скоростей на прямую CD, получим
точки D направлен вдоль направляющих ползуна (рис. 3, а). Проецируя векторы скоростей на прямую CD, получим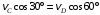 ,
,откуда
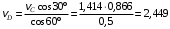 м/с.
м/с.Скорость точки М определим с помощью мгновенного центра скоростей.
Положение мгновенного центра скоростей определим как точку Р пересечения перпендикуляров, проведенных в точках С и D к направлению скоростей этих точек. Запишем выражения, определяющие модули скоростей точек D и M
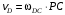 ,
, 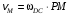 , (8)
, (8)где расстояние
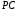 определим из прямоугольного треугольника
определим из прямоугольного треугольника 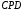 :
: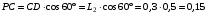 м,
м,а расстояние
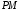 найдем по теореме косинусов из треугольника
найдем по теореме косинусов из треугольника 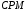 :
: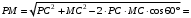
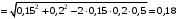 м.
м.Таким образом, будем иметь
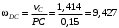 рад/с;
рад/с;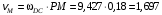 м/с.
м/с.Скорость
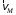 направлена по нормали к прямой МР в сторону поворота шатуна CD (рис. 3, а).
направлена по нормали к прямой МР в сторону поворота шатуна CD (рис. 3, а).5. Определение ускорений точек
 и
и  .
.Выберем за полюс точку С, ускорение которой можно определить. Тогда ускорение точки
 в соответствии с теоремой сложения ускорений будет равно
в соответствии с теоремой сложения ускорений будет равно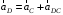 , (8)
, (8)где
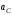 – ускорение полюса;
– ускорение полюса; 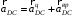 – ускорение точки D во вращении шатуна вокруг полюса.
– ускорение точки D во вращении шатуна вокруг полюса.Поскольку полюс С принадлежит кривошипу, совершающему вращательное движение, то его ускорение равно через составляющие
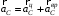 .
.Таким образом,
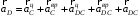 , (9)
, (9)где модули составляющих ускорений будут равны:
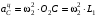 ;
;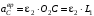 ;
;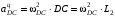 ;
;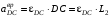 .
.Величину
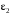 найдем, дифференцируя по времени выражение угловой скорости
найдем, дифференцируя по времени выражение угловой скорости  :
: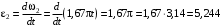 рад/с2.
рад/с2.Так как знаки
 и
и 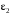 совпадают, то вращение второго колеса, а, следовательно, и кривошипа, ускоренное, т.е. направление вектора
совпадают, то вращение второго колеса, а, следовательно, и кривошипа, ускоренное, т.е. направление вектора 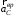 будет совпадать с направлением вектора
будет совпадать с направлением вектора  . Вектор
. Вектор 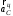 направлен к оси вращения кривошипа 2.
направлен к оси вращения кривошипа 2.Вычисляем модули ускорений, входящих в векторное равенство (9), для
 :
: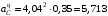
м/с2;
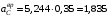 м/с2;
м/с2;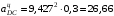 м/с2.
м/с2.Таким образом, в уравнение (9) входят две неизвестные по модулю величины
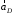 и
и 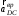 ; линии, по которым эти векторы направлены, известны. Зададим направление этих векторов как указано на рис. 3, б. Теперь спроецируем уравнение (9) на выбранные направления координатных осей
; линии, по которым эти векторы направлены, известны. Зададим направление этих векторов как указано на рис. 3, б. Теперь спроецируем уравнение (9) на выбранные направления координатных осей 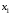 и
и 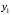 , получим два уравнения, в которые войдут два неизвестных. Проецируя на ось
, получим два уравнения, в которые войдут два неизвестных. Проецируя на ось 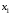 , получим
, получим 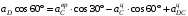 ,
,откуда
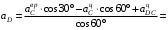
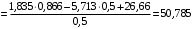 м/с2.
м/с2.Проецируем уравнение (9) на ось
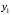 :
: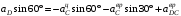 ,
,откуда находим
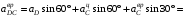
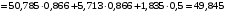 м/с2.
м/с2.Так как знаки положительны, то направления векторов
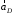 и
и 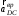 выбраны правильно.
выбраны правильно.Находим угловое ускорение шатуна
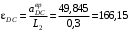 рад/с2.
рад/с2.6. Ускорение точки М находим по векторному уравнению
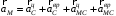 , (10)
, (10)где
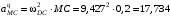 м/с2;
м/с2;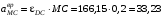 м/с2.
м/с2.Проецируем (1) н оси
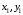 :
: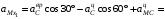
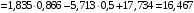 м/с2;
м/с2;