ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 119
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
VII. Работа над развитием логического мышления учащихся.
В заключение урока учитель может предложить детям задание на развитие логического мышления. Например, можно использовать задание на полях учебника (с. 41, часть 1).
VIII. Итог урока.
– Что нового узнали на уроке?
– Какое задание особенно понравилось?
У р о к 26. «РАВЕНСТВО», «НЕРАВЕНСТВО»
Цели урока: познакомить учащихся с терминами «равенство», «неравенство»; формировать умение детей сравнивать числа и правильно использовать знаки сравнения «больше», «меньше», «равно»; продолжать пропедевтику темы «Задача».
Ход урока
I. Организационный момент.
1. Игра «Назови соседа»:
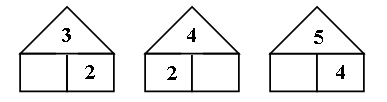
2. Игра «Поход в магазин».
На магнитной доске – увеличенные образцы монет: 1 рубль, 2 рубля, 5 рублей; на наборном полотне – фигурки различных игрушек, посуды, школьных принадлежностей и «ценники» на них.
Один из учеников (дети меняются) исполняет роль продавца, остальные – это «покупатели». «Продавец» должен давать сдачу, если в этом есть необходимость, а также проверять «покупателя», хватит ли у него денег на определённый товар.
Учитель помогает «продавцу».
Если, допустим, ученик выбрал «товар», который стоит 5 рублей, и платит за него монетой в 5 рублей, учитель обязательно должен спросить учеников о том, как по-другому можно заплатить за этот же предмет.
II. Знакомство с терминами «равенство», «неравенство».
Учитель предлагает учащимся внимательно посмотреть на доску, на которой следующая з а п и с ь:
3 – 1 = 2 5 – 1 < 5
4 – 1 > 1 4 + 1 = 5
3 + 1 > 2 1 + 1 = 2
– Что заметили?
– Какие две группы можно выделить?
– Запишите первую группу выражений в столбик в ваших тетрадях. (Учитель делает запись на доске, один из учеников комментирует.)
В результате на доске и у детей в тетрадях появляется з а п и с ь:
3 – 1 = 2
4 + 1 = 5
1 + 1 = 2
– Запишите вторую, выделенную вами, группу во второй столбик.
Учащиеся записывают в тетрадях, учитель – на доске. Один из учеников комментирует.
В результате появляется следующая з а п и с ь:
4 – 1 > 1
5 – 1 < 5
3 + 1 > 2
Учитель спрашивает детей о том, как бы они назвали выражения, записанные в первом столбике.
(Равенства.)
– А как тогда можно назвать записи второго столбика? (Возможно, ученики сами дадут название группе – неравенства.)
– Какой вывод можно сделать? (Если между числами или числовыми выражениями стоит знак «равно», то это равенство, если между числами или числовыми выражениями стоит знак « > » или « < », то это – неравенство.)

III. Сравнение выражений и чисел. Формирование навыка в правильном написании знаков сравнения.
Учитель может использовать задания 3, 5 учебника (с. 44, часть 1).
Задание 3 дети могут выполнить на доске, объяснив выбор знаков.
Задание 5 можно дать как с а м о с т о я т е л ь н у ю работу или работу в парах.
С а м о п р о в е р к а с доски.

IV. Пропедевтика темы «Задача».
Учитель просит детей рассмотреть задание 2 (с. 45 учебника, часть 1).
– Что заметили? (До этого задания учащиеся сами составляли рассказы (задачи) по рисункам, теперь же задача написана, только данные числа по-прежнему нарисованы. Несмотря на то что текст задачи написан, сам термин «задача» ученикам ещё не даётся.)
– Ответьте на поставленный вопрос.
– Какое равенство вы бы записали к этому рассказу?
Далее дети рассматривают рисунки и выражения задания 3 (с. 45 учебника, часть 1), соотносят выражения с рисунками, называют «лишние» выражения.
V. Итог урока.
– Чему научились на уроке?
– Что нового узнали?
– Как вы работали сегодня на уроке?
У р о к 27. МНОГОУГОЛЬНИКИ
Цели урока: познакомить учащихся с различными многоугольниками, повторить состав чисел 2–5; формировать умение детей сравнивать числа и числовые выражения; работать над развитием мышления учащихся.
Ход урока
I. Организационный момент.
II. Изучение нового материала.
1. Знакомство с многоугольниками.
На магнитной д о с к е расположены вырезанные из бумаги геометрические фигуры:
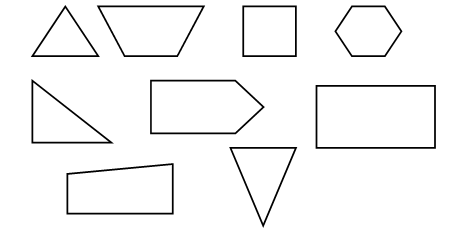
Учитель просит детей внимательно рассмотреть фигуры и разделить их на группы по характерным особенностям.
В результате на доске появляются 2 большие г р у п п ы:
треугольники четырёхугольники
– По какому признаку вы объединили фигуры в группы?
(По количеству углов.)
– Как бы вы назвали фигуры первой группы? (Треугольники.)
– Как бы вы назвали фигуры другой группы? (Четырёхугольники.)
Учитель должен обратить внимание детей на такие разновидности четырёхугольников, как квадрат и прямоугольник.
– Как бы вы назвали оставшиеся фигуры? (Пятиугольник, так как фигура имеет 5 углов, шестиугольник – имеет 6 углов.)
Далее учитель сообщает детям, что и треугольники, и четырёхугольники, и пятиугольники, и шестиугольники – это многоугольники, или геометрические фигуры.
2. Формирование умения различать многоугольники.
Р а б о т а с у ч е б н и к о м.
Учитель предлагает ученикам рассмотреть многоугольники, изображённые на полях учебника (с. 46, часть 1).
– Назовите каждый многоугольник.
– Покажите в нём углы, стороны, вершины. (Прежде чем учащиеся покажут углы, стороны и вершины многоугольников, учитель должен предварительно проделать аналогичную работу с одной из фигур на доске.)

III. Повторение состава изученных чисел.
Работа ведётся по заданию 3 (с. 47 учебника, часть 1) и заданию 1 (с. 12 в тетради № 1).
Выполняя задание учебника, дети рассматривают рисунки и читают равенства, соответствующие рисункам, затем находят значения выражений и проверяют правильность ответа по рисункам.
Например: четыре – это 3 и 1, значит, из четырёх вычесть три – получится один. Пять – это 2 и 3, значит, из пяти вычесть два – получится три. По последнему рисунку учащиеся с а м о с т о я т е л ь н о составляют два равенства и находят их значения.
Работая по тетради, учащиеся рассматривают рисунки и числовые выражения.
– Как вы думаете, какие числовые выражения подходят к рисункам? (4 + 1; 3 + 2.)
– Почему так считаете? ( На первом рисунке нарисовано 3 дубовых листика и 2 кленовых, этому рисунку подходит выражение 3 + 2, на втором рисунке нарисовано 4 дубовых листика и 1 кленовый, ему соответствует выражение 4 + 1, рисунков, которые бы соответствовали выражениям 4 – 2 и 5 – 1, нет.)
– Соедините рисунок с соответствующим выражением.
– Запишите выражения (дети обводят выражения по точкам), найдите значения выражений, проверьте себя, посчитав количество листиков на рисунках.
– Как при помощи данных рисунков можно найти значения оставшихся выражений?
(Значение выражения 5 – 1 можно найти следующим образом: на одном из рисунков зачеркнуть 1 листочек, получится 4. Теперь можно найти значение выражения 4 – 2, зачеркнув ещё 2 листочка на этом же рисунке.)
Учащиеся выполняют работу: зачёркивают необходимое количество листиков, обводят полученные выражения и записывают их значения.

IV. Формирование умения сравнивать числа и числовые выражения.
Учитель предлагает учащимся рассмотреть рисунки в задании 2 (с. 47 учебника, часть 1).
– Сравните пары рисунков.
– Что хотите сказать?
– Какие знаки сравнения следует поставить?
Учащиеся анализируют каждый рисунок и запись под ним и делают в ы в о д о том, какой знак следует поставить.
Например:
На верхней строке нарисовано 4 красных треугольника, а на нижней 2 жёлтых и 2 синих. К двум прибавить два – получится четыре, следовательно, нужно поставить знак «равно». Четыре равно четырём.
С а м о с т о я т е л ь н а я работа учащихся.
Ученики выполняют задание 2 (с. 12 в тетради № 1).
Учитель может также пригласить двух учащихся к доске, и они будут выполнять задание на «закрытой» доске.
Ф р о н т а л ь н а я проверка.
V. Работа над развитием логического мышления учащихся.
В заключение урока детям предлагается задание 3 (с. 46 учебника, часть 1), способствующее развитию мышления детей.
VI. Итог урока.
– Что нового открыли для себя на уроке?
– Понравилась ли вам ваша работа на уроке?
У р о к 28. ЗАКРЕПЛЕНИЕ И ОБОБЩЕНИЕ ЗНАНИЙ
УЧАЩИХСЯ ПО ТЕМЕ «ЧИСЛА 1–5. СОСТАВ ЧИСЕЛ 2–5».
ЧЕРЧЕНИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР
Цели урока: проверить, как учащиеся усвоили состав изученных чисел, как у детей сформирован навык прямого и обратного счёта (от 1 до 5, от 5 до 1); закреплять знания учащихся о многоугольниках, учить детей чертить многоугольники по линейке, учить правильно пользоваться линейкой; прививать аккуратность.
Ход урока
I. Организационный момент.
II. Закрепление и обобщение знаний учащихся о числах 1–5 и составе чисел 2–5.
1. Игра «Путаница».
На д о с к е (или магнитной доске, наборном полотне) записаны числа:
4 1 3 2 5
– Что заметили?
– Расположите числа по порядку.
Учащиеся могут расположить числа двумя способами.
(1 2 3 4 5 5 4 3 2 1.)
Учитель спрашивает учащихся о том, как называется порядок, когда числа расположены от меньшего к большему, и сообщает детям о том, что порядок увеличения можно назвать и по-другому: порядок возрастания. После этого учащиеся вспоминают, что порядок, в котором числа расположены от большего к меньшему, называется порядком уменьшения, а учитель сообщает ученикам о том, что данный порядок можно назвать и по-другому: порядок убывания.
2. Игра «Назови соседа».
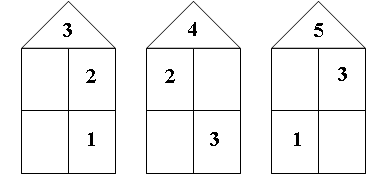
Данная игра позволяет учителю проверить, как учащиеся усвоили состав изученных чисел, а ученикам – закрепить знание состава этих чисел.
3. Упражнение в умении соотносить число и цифру.
Р а б о т а в т е т р а д и.
Далее учитель предлагает учащимся рассмотреть задания 3, 4 (с. 12 в тетради № 1).
– Как вы думаете, какую работу необходимо выполнить в этих заданиях? (В задании 3 записать соответствующей цифрой количество изображённых предметов, в задании 4 нарисовать такое количество фигур, которое соответствует написанной цифре).
С а м о с т о я т е л ь н а я р а б о т а у ч а щ и х с я.
В з а и м о п р о в е р к а.

III. Повторение изученного о многоугольниках.
На д о с к е расположено несколько различных многоугольников (но меньше, чем на предыдущем уроке).
– Как назвать все фигуры общим словом? (Многоугольники, геометрические фигуры.)
Далее учитель указывает на одну из фигур:
– Как ещё можно назвать эту фигуру?
– Как вы это узнали? (По количеству углов.)
Затем учитель поочерёдно показывает на квадрат и прямоугольник.
– Как по-разному можно назвать эту фигуру? (Многоугольник, четырёхугольник, прямоугольник, квадрат.)
Р а б о т а в т е т р а д и.
Учащиеся, выполняя задание 5 (с. 12 в тетради № 1), закрашивают только пятиугольники.
После в з а и м о п р о в е р к и учитель спрашивает учащихся о том, какие фигуры остались незакрашенными.
IV. Изучение нового материала.