ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 123
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(Дети могут сказать, что число 5 следует за числом 4; что 5 – нечётное число; что 5 больше чисел 1, 2, 3, 4 и т. д.)
– Число 5 записывается с помощью цифры 5.(Увеличенный образец цифры 5 учитель вывешивает на доску.)
III. Анализ образца, письмо цифры 5.
– На что, по вашему мнению, похожа цифра 5?
– А вот поэту она напомнила фокусника:
Это – фокусник – пятёрка.
Вы за ней следите зорко.
Кувыркнётся – раз и два! –
Обернётся цифрой «два».
Г. Виеру
Далее следует анализ образца цифры и письмо цифры по этапам:
в воздухе;
по точкам;
самостоятельное письмо в тетради (с. 9 в тетради № 1, задание 2).

IV. Упражнение в прямом и обратном счёте предметов.
Учитель. А теперь мы – строители. Мы будем строить башню из кубиков. (Для этого задания можно использовать детские кубики.)
– Итак, берём 1 кубик – один.
– Ставим на него следующий – два.
– На него ещё один – три.
– Добавляем ещё – четыре.
– И последний – пять.
– Посчитаем хором этажи башни. (Один – два – три – четыре – пять.)
Счёт сопровождается показом соответствующего кубика.
– А теперь сложим кубики обратно в коробку.
– Сколько этажей у башни? (Пять.)
– Уберём один кубик. Сколько осталось? (Четыре.)
– Уберём ещё один. Сколько осталось? (Три.)
– Уберём ещё один. Сколько кубиков осталось? (Два.)
– Уберём ещё один кубик. Сколько осталось? (Один.)
– Посчитаем хором. (Пять – четыре – три – два – один.)
Р а б о т а с у ч е б н и к о м.
– Посмотрите на рисунок 2 (с. 32, часть 1).
– Что на нём изображено? (Геометрические фигуры: круги и треугольники.)
– Сколько кругов? (Пять.)
– Сколько треугольников? (Пять.)
– Как получили 5 кругов? (К четырём прибавили один.)
– Как получили 5 треугольников? (К трём прибавили два.)
Далее учитель может познакомить учащихся с монетой – 5 рублей, а затем поупражнять детей в наборе различных сумм разными монетами.
– Матрёшка стоит 5 рублей. Какими монетами можно заплатить за матрёшку? Как это сделать разными способами? (Учитель записывает на доске все варианты: 1 + 1 + 1 + 1 + 1; 2 + 1 + 1 + 1; 2 + 2 + 1; 5.)
– Перчатки стоят три рубля. Какими монетами можно заплатить за них?
– Можно ли заплатить монетой в 5 рублей?
– Сколько сдачи должен будет дать продавец? (Для того чтобы посчитать сдачу, дети могут использовать счётный материал наборного полотна или рисунок в учебнике.)

V. Пропедевтика темы «Задача».
По рисункам в задании 2 (с. 33 учебника, часть 1) и задании 1 (с. 9 в тетради № 1) учащиеся составляют короткие (математические) рассказы и ставят вопросы к ним.
И в тетради, и в учебнике есть «лишние» выражения, дети должны не только догадаться, какое из выражений является «лишним», но и обосновать своё мнение. К оставшимся выражениям ученики могут придумать свои рассказы.
VI. Работа над развитием внимания, наблюдательности учащихся.
В заключение урока ученики выполняют задание, требующее наблюдательности: «Сравни картинки и найди 5 отличий» (с. 33 учебника, часть 1). Учитель может провести выполнение этого задания в форме игры «Кто самый внимательный?».
VII. Итог урока.
– Чему учились?
– Что нового узнали на уроке?
– Было ли вам интересно на уроке?
– Что особенно понравилось?
У р о к 21. СОСТАВ ЧИСЛА 5
Цели урока: показать учащимся, как можно получить число 5; учить детей различать понятия «число» и «цифра» и правильно пользоваться данными терминами; продолжать работу по соотнесению числа с соответствующей цифрой.
Ход урока
I. Организационный момент.
II. Повторение пройденного о числах 1–5. Соотнесение чисел с цифрами, их обозначающими.
Начать работу можно с выполнения заданий в тетради (задания 2, 3, с. 10 в тетради № 1).
Учитель предлагает ученикам рассмотреть внимательно задание 3.
– Как вы думаете, какую работу предстоит выполнить в данном задании? (Соединить рисунок с цифрой, показывающей число предметов.)
– Выполните задание.
С а м о с т о я т е л ь н а я работа учащихся.
В з а и м о п р о в е р к а.
Далее дети выполняют первую часть задания 2.
– Какая цифра написана? (5.)
– Обведите по контурам и закрасьте такое число треугольников, которое соответствует записанной цифре.
– Проверьте работу друг друга.
После этого задания учащиеся под диктовку учителя записывают в столбик следующие цифры: 4, 2, 3, 1.
Один из учеников после выполнения работы в тетради записывает цифры на доске.
С а м о п р о в е р к а с доски.
– Около цифры 4 нарисуйте такое количество яблок, которое соответствует записанной цифре.
– Около цифры 2 нарисуйте соответствующее число грибов.
– Около цифры 3 – соответствующее число слив.
– Около цифры 1 – соответствующее число морковок.
– Проверьте работу друг друга.

III. Изучение нового материала.
1. Формирование восприятия состава числа 5.
Работу можно провести по рисунку 1 (с. 34 учебника, часть 1) или с использованием наборного полотна.
– Рассмотрите внимательно рисунок.
– Что заметили? (На двух лавочках сидят пять девочек.)
– Как девочки расположились на лавочках? (Сначала на одной лавочке сидели четыре девочки, а на другой – одна девочка.)
Параллельно на наборном полотне или магнитной д о с к е «записывается»: 4 1.
Потом на одной лавочке осталось три девочки, а на другой стало – две.
З а п и с ь на наборном полотне (магнитной доске): 3 2.
Потом на первой лавочке осталось сидеть две девочки, а на второй стало три девочки.
З а п и с ь на наборном полотне (магнитной доске): 2 3 .
Затем ещё одна девочка пересела на вторую лавочку, и на первой лавочке осталась одна девочка, а на второй их стало четыре.
З а п и с ь на наборном полотне (магнитной доске): 1 4.
– Посмотрите на записи, сделанные на доске.
– Пользуясь записями, расскажите, как можно получить число 5.
Учащиеся проговаривают хором:
Пять – это четыре и один.
Пять – это три и два.
Пять – это два и три.
Пять – это один и четыре.
2. Упражнение в получении числа 5 разными способами.
Далее учитель может провести с детьми игру «Заселяем домик».
Можно использовать «домик», помещённый на полях учебника (с. 34, часть 1), но лучше, чтобы «домик» был на доске и дети «заселяли» его магнитными цифрами.

IV. Закрепление знаний учащихся о составе числа 5.
Подготовка к восприятию темы «Связь сложения и вычитания».
Учитель предлагает ученикам рассмотреть рисунок в задании 2 (с. 34 учебника, часть 1).
– Что хотите сказать? (С помощью бусинок показан состав числа 5.)
Далее дети записывают на доске или на наборном полотне: 4 + 1 = 5.
– Если от 5 бусинок убрать одну, сколько бусинок останется? (Четыре).
З а п и с ь: 5 – 1 = 4.
В итоге на д о с к е (наборном полотне) появляется следующая запись:
4 + 1 = 5 5 – 1 = 4
3 + 2 = 5 5 – 2 = 3
2 + 3 = 5 5 – 3 = 2
1 + 4 = 5 5 – 4 = 1
– Какой вывод можно сделать?
В заключение урока учащиеся выполняют задание 1 (с. 35 учебника, часть 1): сравнивают числа (устно). Задание выполняется фронтально.
V. Итог урока.
– Что нового узнали?
– Чему научились?
– Оцените свою работу.
У р о к 22. ТОЧКА. КРИВАЯ ЛИНИЯ.
ПРЯМАЯ ЛИНИЯ. ОТРЕЗОК
Цели урока: дать учащимся первичные представления о кривой линии, прямой линии, отрезке; продолжать работу по усвоению учащимися состава чисел 2–5; продолжать пропедевтику темы «Задача».
Ход урока
I. Организационный момент.
II. Изучение нового материала.
1. Знакомство с новыми понятиями.
На доске изображено несколько разных линий.
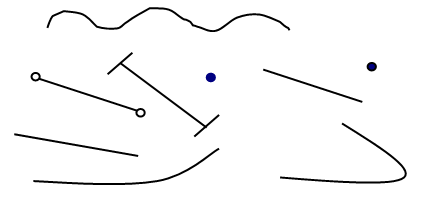
Учитель просит детей внимательно посмотреть на доску и сказать, что они заметили.
В результате беседы учащиеся под руководством учителя делят все изображённые на доске объекты на 4 г р у п п ы:
точки, кривые линии, прямые линии, отрезки.
2. Графическое изображение изученных линий. Выводы.
– Чем прямая линия отличается от кривой?
– Каким чертёжным инструментом нужно воспользоваться, чтобы начертить прямую линию? (Линейкой.)
– Как вы думаете, почему линейку так назвали?
– Про линейку даже есть стихотворение:
Я – линейка. Прямота –
Моя главная черта.
– Начертите в ваших тетрадях одну прямую линию и одну кривую.
– Нужна ли линейка, для того чтобы начертить кривую линию?
– Поставьте в ваших тетрадях точку.
– Как вы думаете, сколько прямых линий можно провести через одну точку? (Высказывания детей.)
– Проведите одну прямую линию.
– Можно ли провести ещё?
– Проведите.
– А ещё можно провести прямую линию через эту же точку?
– Проведите.
– А ещё можно?
– Проведите.
– Какой в ы в о д можно сделать? (Через одну точку можно провести бесконечно много прямых линий.)
– Как вы думаете, можно ли через одну точку провести бесконечно много кривых линий?
– Попробуйте это сделать.
– Какой вывод из этого следует?
– А теперь поставьте в ваших тетрадях две точки.
– Сколько через них можно провести прямых линий? (Высказывания детей.)
– Проведите прямую линию.
– Проведите ещё одну прямую через эти же точки. (Дети пытаются выполнить задание учителя и приходят к выводу, что это сделать невозможно.)
– Получилось ли у вас это сделать?
– Какой в ы в о д из этого следует? (Через две точки можно провести только одну прямую линию.)
– Поставьте ещё две точки в ваших тетрадях.
– Сколько кривых можно провести через них?
– Проведите одну кривую линию.
– Можно ли провести ещё одну кривую линию через эти же две точки?
– Попробуйте это сделать.
– А ещё одну?
– Проведите.
– Какой в ы в о д из этого следует? (Через две точки можно провести много кривых линий.)
– Проведите прямую линию.
– Поставьте на ней две точки.
– Часть прямой от одной точки до другой выделите цветным карандашом.
– Посмотрите внимательно на доску и найдите линии, похожие на полученную вами.
– Как называются эти линии? (Отрезки.)
– Чем отрезок отличается от прямой линии?
Учитель помогает детям сделать в ы в о д. (Отрезок – это часть прямой линии. Отрезок имеет начало и конец, то есть ограничен с двух сторон точками, в отличие от прямой линии, которая не имеет ни начала, ни конца, то есть бесконечна.)
– Начертите в ваших тетрадях два отрезка.
В з а и м о п р о в е р к а.

III. Пропедевтика темы «Задача».
Учитель предлагает учащимся рассмотреть задание 2 (с. 37 учебника, часть 1).
– Как вы думаете, какое задание предстоит выполнить?
– Составьте рассказы и поставьте к ним вопросы.
– Какое числовое выражение соответствует первому рисунку?
– Какое числовое выражение соответствует второму рисунку?
– Какие числовые выражения оказались «лишними»?
– Составьте по ним рассказы.

– Число 5 записывается с помощью цифры 5.(Увеличенный образец цифры 5 учитель вывешивает на доску.)
III. Анализ образца, письмо цифры 5.
– На что, по вашему мнению, похожа цифра 5?
– А вот поэту она напомнила фокусника:
Это – фокусник – пятёрка.
Вы за ней следите зорко.
Кувыркнётся – раз и два! –
Обернётся цифрой «два».
Г. Виеру
Далее следует анализ образца цифры и письмо цифры по этапам:
в воздухе;
по точкам;
самостоятельное письмо в тетради (с. 9 в тетради № 1, задание 2).

IV. Упражнение в прямом и обратном счёте предметов.
Учитель. А теперь мы – строители. Мы будем строить башню из кубиков. (Для этого задания можно использовать детские кубики.)
– Итак, берём 1 кубик – один.
– Ставим на него следующий – два.
– На него ещё один – три.
– Добавляем ещё – четыре.
– И последний – пять.
– Посчитаем хором этажи башни. (Один – два – три – четыре – пять.)
Счёт сопровождается показом соответствующего кубика.
– А теперь сложим кубики обратно в коробку.
– Сколько этажей у башни? (Пять.)
– Уберём один кубик. Сколько осталось? (Четыре.)
– Уберём ещё один. Сколько осталось? (Три.)
– Уберём ещё один. Сколько кубиков осталось? (Два.)
– Уберём ещё один кубик. Сколько осталось? (Один.)
– Посчитаем хором. (Пять – четыре – три – два – один.)
Р а б о т а с у ч е б н и к о м.
– Посмотрите на рисунок 2 (с. 32, часть 1).
– Что на нём изображено? (Геометрические фигуры: круги и треугольники.)
– Сколько кругов? (Пять.)
– Сколько треугольников? (Пять.)
– Как получили 5 кругов? (К четырём прибавили один.)
– Как получили 5 треугольников? (К трём прибавили два.)
Далее учитель может познакомить учащихся с монетой – 5 рублей, а затем поупражнять детей в наборе различных сумм разными монетами.
– Матрёшка стоит 5 рублей. Какими монетами можно заплатить за матрёшку? Как это сделать разными способами? (Учитель записывает на доске все варианты: 1 + 1 + 1 + 1 + 1; 2 + 1 + 1 + 1; 2 + 2 + 1; 5.)
– Перчатки стоят три рубля. Какими монетами можно заплатить за них?
– Можно ли заплатить монетой в 5 рублей?
– Сколько сдачи должен будет дать продавец? (Для того чтобы посчитать сдачу, дети могут использовать счётный материал наборного полотна или рисунок в учебнике.)

V. Пропедевтика темы «Задача».
По рисункам в задании 2 (с. 33 учебника, часть 1) и задании 1 (с. 9 в тетради № 1) учащиеся составляют короткие (математические) рассказы и ставят вопросы к ним.
И в тетради, и в учебнике есть «лишние» выражения, дети должны не только догадаться, какое из выражений является «лишним», но и обосновать своё мнение. К оставшимся выражениям ученики могут придумать свои рассказы.
VI. Работа над развитием внимания, наблюдательности учащихся.
В заключение урока ученики выполняют задание, требующее наблюдательности: «Сравни картинки и найди 5 отличий» (с. 33 учебника, часть 1). Учитель может провести выполнение этого задания в форме игры «Кто самый внимательный?».
VII. Итог урока.
– Чему учились?
– Что нового узнали на уроке?
– Было ли вам интересно на уроке?
– Что особенно понравилось?
У р о к 21. СОСТАВ ЧИСЛА 5
Цели урока: показать учащимся, как можно получить число 5; учить детей различать понятия «число» и «цифра» и правильно пользоваться данными терминами; продолжать работу по соотнесению числа с соответствующей цифрой.
Ход урока
I. Организационный момент.
II. Повторение пройденного о числах 1–5. Соотнесение чисел с цифрами, их обозначающими.
Начать работу можно с выполнения заданий в тетради (задания 2, 3, с. 10 в тетради № 1).
Учитель предлагает ученикам рассмотреть внимательно задание 3.
– Как вы думаете, какую работу предстоит выполнить в данном задании? (Соединить рисунок с цифрой, показывающей число предметов.)
– Выполните задание.
С а м о с т о я т е л ь н а я работа учащихся.
В з а и м о п р о в е р к а.
Далее дети выполняют первую часть задания 2.
– Какая цифра написана? (5.)
– Обведите по контурам и закрасьте такое число треугольников, которое соответствует записанной цифре.
– Проверьте работу друг друга.
После этого задания учащиеся под диктовку учителя записывают в столбик следующие цифры: 4, 2, 3, 1.
Один из учеников после выполнения работы в тетради записывает цифры на доске.
С а м о п р о в е р к а с доски.
– Около цифры 4 нарисуйте такое количество яблок, которое соответствует записанной цифре.
– Около цифры 2 нарисуйте соответствующее число грибов.
– Около цифры 3 – соответствующее число слив.
– Около цифры 1 – соответствующее число морковок.
– Проверьте работу друг друга.

III. Изучение нового материала.
1. Формирование восприятия состава числа 5.
Работу можно провести по рисунку 1 (с. 34 учебника, часть 1) или с использованием наборного полотна.
– Рассмотрите внимательно рисунок.
– Что заметили? (На двух лавочках сидят пять девочек.)
– Как девочки расположились на лавочках? (Сначала на одной лавочке сидели четыре девочки, а на другой – одна девочка.)
Параллельно на наборном полотне или магнитной д о с к е «записывается»: 4 1.
Потом на одной лавочке осталось три девочки, а на другой стало – две.
З а п и с ь на наборном полотне (магнитной доске): 3 2.
Потом на первой лавочке осталось сидеть две девочки, а на второй стало три девочки.
З а п и с ь на наборном полотне (магнитной доске): 2 3 .
Затем ещё одна девочка пересела на вторую лавочку, и на первой лавочке осталась одна девочка, а на второй их стало четыре.
З а п и с ь на наборном полотне (магнитной доске): 1 4.
– Посмотрите на записи, сделанные на доске.
– Пользуясь записями, расскажите, как можно получить число 5.
Учащиеся проговаривают хором:
Пять – это четыре и один.
Пять – это три и два.
Пять – это два и три.
Пять – это один и четыре.
2. Упражнение в получении числа 5 разными способами.
Далее учитель может провести с детьми игру «Заселяем домик».
Можно использовать «домик», помещённый на полях учебника (с. 34, часть 1), но лучше, чтобы «домик» был на доске и дети «заселяли» его магнитными цифрами.

IV. Закрепление знаний учащихся о составе числа 5.
Подготовка к восприятию темы «Связь сложения и вычитания».
Учитель предлагает ученикам рассмотреть рисунок в задании 2 (с. 34 учебника, часть 1).
– Что хотите сказать? (С помощью бусинок показан состав числа 5.)
Далее дети записывают на доске или на наборном полотне: 4 + 1 = 5.
– Если от 5 бусинок убрать одну, сколько бусинок останется? (Четыре).
З а п и с ь: 5 – 1 = 4.
В итоге на д о с к е (наборном полотне) появляется следующая запись:
4 + 1 = 5 5 – 1 = 4
3 + 2 = 5 5 – 2 = 3
2 + 3 = 5 5 – 3 = 2
1 + 4 = 5 5 – 4 = 1
– Какой вывод можно сделать?
В заключение урока учащиеся выполняют задание 1 (с. 35 учебника, часть 1): сравнивают числа (устно). Задание выполняется фронтально.
V. Итог урока.
– Что нового узнали?
– Чему научились?
– Оцените свою работу.
У р о к 22. ТОЧКА. КРИВАЯ ЛИНИЯ.
ПРЯМАЯ ЛИНИЯ. ОТРЕЗОК
Цели урока: дать учащимся первичные представления о кривой линии, прямой линии, отрезке; продолжать работу по усвоению учащимися состава чисел 2–5; продолжать пропедевтику темы «Задача».
Ход урока
I. Организационный момент.
II. Изучение нового материала.
1. Знакомство с новыми понятиями.
На доске изображено несколько разных линий.

Учитель просит детей внимательно посмотреть на доску и сказать, что они заметили.
В результате беседы учащиеся под руководством учителя делят все изображённые на доске объекты на 4 г р у п п ы:
точки, кривые линии, прямые линии, отрезки.
2. Графическое изображение изученных линий. Выводы.
– Чем прямая линия отличается от кривой?
– Каким чертёжным инструментом нужно воспользоваться, чтобы начертить прямую линию? (Линейкой.)
– Как вы думаете, почему линейку так назвали?
– Про линейку даже есть стихотворение:
Я – линейка. Прямота –
Моя главная черта.
– Начертите в ваших тетрадях одну прямую линию и одну кривую.
– Нужна ли линейка, для того чтобы начертить кривую линию?
– Поставьте в ваших тетрадях точку.
– Как вы думаете, сколько прямых линий можно провести через одну точку? (Высказывания детей.)
– Проведите одну прямую линию.
– Можно ли провести ещё?
– Проведите.
– А ещё можно провести прямую линию через эту же точку?
– Проведите.
– А ещё можно?
– Проведите.
– Какой в ы в о д можно сделать? (Через одну точку можно провести бесконечно много прямых линий.)
– Как вы думаете, можно ли через одну точку провести бесконечно много кривых линий?
– Попробуйте это сделать.
– Какой вывод из этого следует?
– А теперь поставьте в ваших тетрадях две точки.
– Сколько через них можно провести прямых линий? (Высказывания детей.)
– Проведите прямую линию.
– Проведите ещё одну прямую через эти же точки. (Дети пытаются выполнить задание учителя и приходят к выводу, что это сделать невозможно.)
– Получилось ли у вас это сделать?
– Какой в ы в о д из этого следует? (Через две точки можно провести только одну прямую линию.)
– Поставьте ещё две точки в ваших тетрадях.
– Сколько кривых можно провести через них?
– Проведите одну кривую линию.
– Можно ли провести ещё одну кривую линию через эти же две точки?
– Попробуйте это сделать.
– А ещё одну?
– Проведите.
– Какой в ы в о д из этого следует? (Через две точки можно провести много кривых линий.)
– Проведите прямую линию.
– Поставьте на ней две точки.
– Часть прямой от одной точки до другой выделите цветным карандашом.
– Посмотрите внимательно на доску и найдите линии, похожие на полученную вами.
– Как называются эти линии? (Отрезки.)
– Чем отрезок отличается от прямой линии?
Учитель помогает детям сделать в ы в о д. (Отрезок – это часть прямой линии. Отрезок имеет начало и конец, то есть ограничен с двух сторон точками, в отличие от прямой линии, которая не имеет ни начала, ни конца, то есть бесконечна.)
– Начертите в ваших тетрадях два отрезка.
В з а и м о п р о в е р к а.

III. Пропедевтика темы «Задача».
Учитель предлагает учащимся рассмотреть задание 2 (с. 37 учебника, часть 1).
– Как вы думаете, какое задание предстоит выполнить?
– Составьте рассказы и поставьте к ним вопросы.
– Какое числовое выражение соответствует первому рисунку?
– Какое числовое выражение соответствует второму рисунку?
– Какие числовые выражения оказались «лишними»?
– Составьте по ним рассказы.
