Добавлен: 06.02.2019
Просмотров: 15909
Скачиваний: 9
51
превышает 0.01–1 аФ [120, 128], что значительно меньше величины «геометрической»
емкости в этой конфигурации. Столь же низкие значения емкости были определены пу-
тем анализа импульсного отклика зазора на малых временах с использованием субпи-
косекундного лазера [251]. Экспериментальные оценки, полученные из анализа изме-
нения эффективной высоты туннельного барьера при адсорбции [208], и квантово-
химические расчеты [252–254] емкости для отдельных молекул также приводят к столь
же низким значениям. Характер зависимости емкости от расстояния, по данным раз-
личных исследователей, колеблется от классической обратной пропорциональности до
экспоненциальной зависимости. Все это слабо согласуется как с представленными вы-
ше данными, так и с результатами измерения в конфигурации сканирующего емкостно-
го микроскопа (scanning capacitance microscopy, SCM) и микроскопии электростатиче-
ских сил (electrostatic force microscopy, EFM). Некоторые исследователи [255, 256] вы-
сказывали предположение о том, что в условиях туннельного переноса электрона мож-
но выделить, наряду с классической «геометрической» емкостью C=dQ/dU, также ем-
кость (названную авторами «электрохимической»), связанную с изменением химиче-
ского потенциала электрона C=e dQ/d
μ. На наноуровне эти два типа величин емкости
могут не совпадать, и «электрохимическая» емкость, определяющая, в частности, пове-
дение частиц в условиях кулоновской блокады, может быть значительно меньше «гео-
метрической». Прямые измерения емкости туннельного зазора не позволили обнару-
жить неклассическое поведение измеряемой емкости. Так, исследования [257], выпол-
ненные в ex situ конфигурации для поверхности золота, покрытого слоем октандитиола,
показали симбатное увеличение емкости и проводимости зазора. Лишь в [245] были
обнаружены признаки снижения емкости с ростом проводимости туннельного зазора
(уменьшения расстояния зонд/образец), однако этот эффект мог быть связан и с аппа-
ратурными погрешностями.
Попытки картирования изменения емкости зазора вдоль поверхности одновре-
менно с топографическими измерениями с использованием синхронного усилителя
[247] показали для металлических и углеродных материалов перепад емкости в различ-
ных точках кадра, не превышающий 60 аФ. Это согласуется с локальной топографиче-
ской картиной. Теоретические оценки, выполненные в [247], показали, что при диамет-
ре зонда 150 нм разрешение метода при картировании вдоль поверхности составляет
около 50 нм. Попытки изучения данным методом гетерогенного материала (золото-
полимерной композиции) были сделаны в [258]. При картировании (одновременно с
топографическими измерениями) синфазной и сдвинутой на 90
о
переменных состав-
ляющих туннельного тока на картах наблюдалась инверсия контраста: области с более

52
высокой проводимостью имели меньшую локальную емкость (рис. 26). Авторы [258]
отмечали, что емкостная карта характеризуется, как правило, более высоким контра-
стом (большим перепадом значений), чем карта локальной проводимости. Нужно отме-
тить, что это единственная работа, в которой проведено картирование с использовани-
ем цифровой обработки сигнала (без использования внешнего синхронного детектора),
с малой амплитудой переменного сигнала. В ней впервые показана информативность
этого подхода для характеристики гетерогенного композиционного материала. В [258]
при картировании не проводилось вычитания аппаратного сдвига фаз, возникающего в
электронных схемах микроскопа (не была проведена точная калибровка), поэтому, как
отмечали сами авторы, возможно частичное перераспределение интенсивности сигнала
между картами. Тем не менее, такое перераспределение не может объяснить столь су-
щественных различий в контрастности карт емкости и проводимости.
Рис. 26. Топографическое изображение (а) и карта амплитуды синфазной (б) и сдвину-
той на 90
о
(в) составляющих туннельного тока, полученные на образце золото-
полимерного композиционного материала. Размер кадра 187 нм. Амплитуда возбуж-
дения 20 мВ [258].
1.1.3.5. Поверхностный потенциал
Метод измерения изменений поверхностного потенциала, ставший стандартным
для атомно-силовой микроскопии (electrostatic force microscopy, Kelvin probe micros-
copy) может быть реализован и в конфигурации СТМ. Нужно отметить, что СТМ кон-
фигурация обеспечивает измерение поверхностного потенциала в условиях протекания
тока, что не может быть реализовано в условиях АСМ. Очевидно, что при синусои-
дальных вертикальных колебаниях зонда наблюдается и синусоидальное колебание
туннельного тока [259–263]. Кроме того, в системе появляется составляющая тока (та-
кая же, как и при колебании кантеливера в конфигурации АСМ), отвечающая переза-
рядке емкости в туннельном зазоре. Эти две составляющие тока могут быть разделены
с помощью синхронного усилителя, так как туннельный ток изменяется синфазно с ко-
лебанием зонда, а ток перезарядки — сдвинут по фазе на 90
о
. Ток перезарядки может
быть записан как [263]
а
б
в
53
1
d
(
)
d
D
tun
surf
C
I
H U
U
H
= ω
−
⋅
, (39)
где H
1
— амплитуда колебаний зонда,
2
ω= πν — циклическая частота колебаний,
U
surf
— поверхностный потенциал. Для модели плоского конденсатора
2
0
d / d
1/
C
H
H
∝
,
а для модели сферы и плоскости (r > H
0
)
0
0
d / d
2
/
C
H
r H
≈− πεε
, где H
0
— среднее рас-
стояние между зондом и образцом [263]. Близкое выражение было получено и в [259].
Даже при нулевом внешнем напряжении между электродами из разных материалов су-
ществует поверхностная разность потенциалов, которая может быть получена из анали-
за зависимости I
D
от туннельного напряжения. Анализ зависимости I
D
от расстояния
позволяет также оценить величину радиуса кончика зонда и абсолютного расстояния
между электродами. В случае полупроводниковых материалов значительный вклад в
емкость туннельного зазора вносит формирующаяся в приповерхностном слое область
обеднения вблизи зонда (рис. 27), что позволяет, в частности, определять тип носителей
заряда и их концентрацию в полупроводнике с высоким разрешением [261]. Следует
отметить, что корректное определение фазовых характеристик сигнала (из-за низких
резонансных частот пьезодвигателя) представляет собой достаточно серьезную про-
блему. В [262] был предложен алгоритм численного разделения вкладов туннельного и
емкостного токов в общий измеряемый ток, и было показано хорошее согласие между
экспериментальными данными и модельными оценками. В [263] был предложен более
простой способ «калибровки» аппаратного сдвига фаз по максимальной интенсивности
емкостного тока на большом удалении от поверхности и туннельного тока вблизи по-
верхности. Тем не менее, широкого распространения данный метод не получил.
а
б
Рис. 27. Модельные зависимости туннельного тока и тока смещения I
D
(а) [262]. Рас-
считанные зависимости тока смещения I
D
от туннельного напряжения для полупро-
водникового материала с различной концентрацией носителей (б) [261]. Пунктирная
линия отвечает теоретической зависимости для металлического электрода.
Положительный знак напряжения отвечает положительному потенциалу зонда.
54
1.1.3.6. Субатомарное разрешение (tapping mode)
В [205] было показано, что увеличение амплитуды колебания зонда при картиро-
вании величины dI/dH приводит к значительному улучшению разрешения и чувстви-
тельности метода за счет кратковременного сильного электронного перекрывания в
момент наибольшего сближения электродов. Логическим продолжением работ в этом
направлении стала реализация топографического метода, аналогичного, по сути, полу-
контактному режиму АСМ (tapping mode). С целью значительного улучшения локаль-
ности в [30, 264–266] было предложено использовать вертикальные колебания зонда с
амплитудой 0,5-1,0 нм и средний ток в качестве разностного сигнала для петли обрат-
ной связи. Как и в случае полуконтактного режима АСМ, основной вклад в разностный
сигнал вносит ток, протекающий в момент максимального сближения, а малая продол-
жительность токового импульса позволяет избежать повреждения электродов. При ис-
пользовании зондов, изготовленных из переходных металлов с разным электронным
строением, было продемонстрировано субатомарное разрешение метода (рис. 28). Близ-
кие результаты были получены ранее и в конфигурации атомно-силового микроскопа
[267, 268]. Этим же методом может с высокой точностью картироваться кажущаяся вы-
сота туннельного барьера (локальная работа выхода) с атомарным разрешением [265].
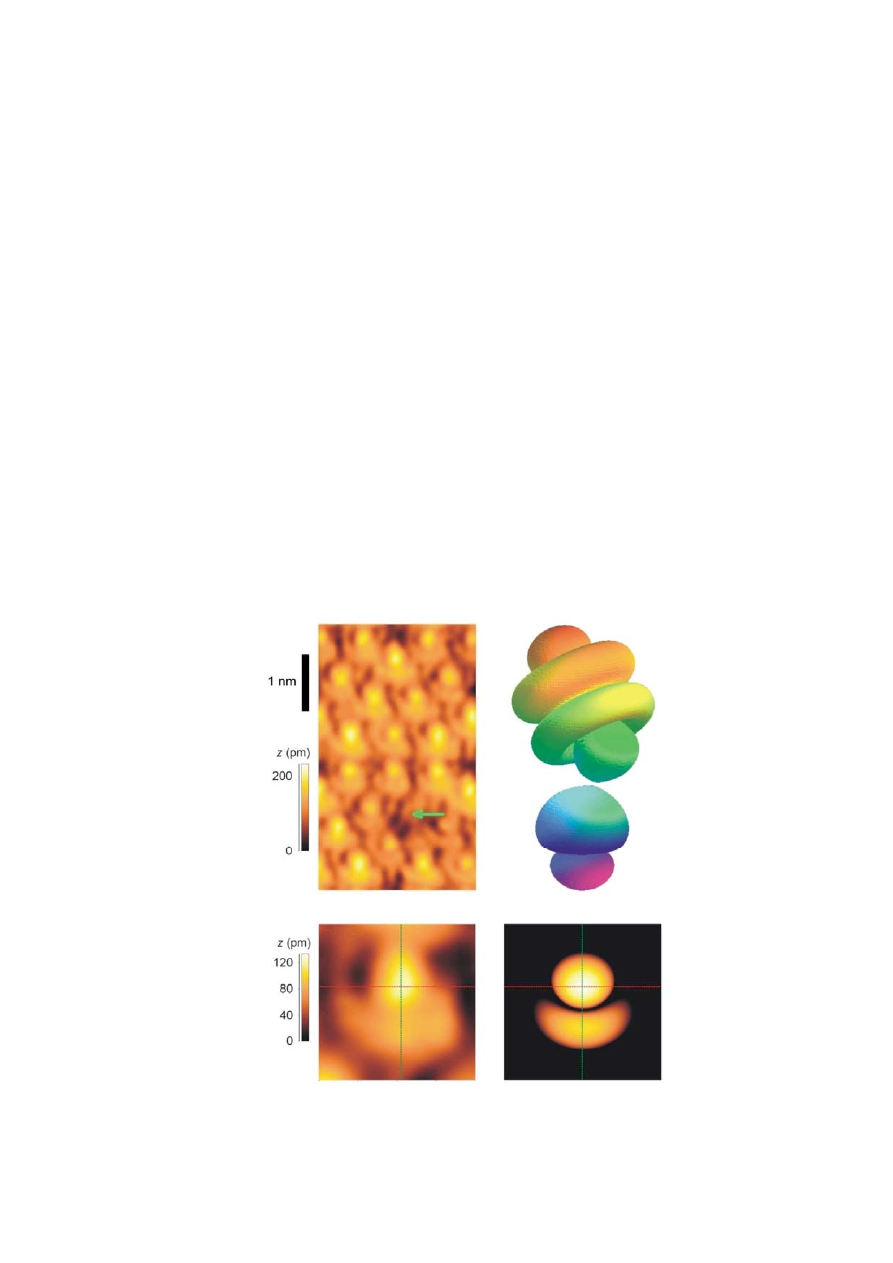
Рис. 28. СТМ изображение сверхвысокого разрешения поверхности Si(111)-(7x7),
полученное в динамическом режиме с использованием зонда, изготовленного из
Co
6
Fe
3
Sm (а). Схематическое изображение орбиталей Si sp
3
и Sm 4f
z3
(наклонена на
угол ~37
о
), отвечающих за протекание тока (б). Экспериментальное (в) и расчетное (г)
изображения отдельного атома [30].
б
а
в
г
55
Нужно отметить, что близкая идеология используется также для изучения чел-
ночного переноса электрона [269], например, в условиях кулоновской блокады, когда
на вольтамперных зависимостях наблюдаются области NDR [270, 271].
1.2. Особенности туннельной спектроскопии
в электрохимической in situ конфигурации
Переход от СТМ-измерений в условиях высокого вакуума к измерениям на возду-
хе и в растворах был закономерен как с точки зрения упрощения и удешевления обору-
дования, так и с точки зрения расширения круга исследуемых объектов. Первые изме-
рения в водных растворах были проведены в 1986 г. [272, 273], и уже тогда было про-
демонстрирована возможность получения атомарного разрешения на HOPG в растворе.
Метод нашел широкое применение для исследования разнообразных явлений на меж-
фазной границе твердое тело/жидкоть, таких как адсорбция, поверхностная диффузия,
процессы образования новой фазы, коррозия, окислительно-восстановительные про-
цессы отдельных молекул и др. [274–280]. Тем не менее, до сих пор востребованной в
таких исследованиях является исключительно топографическая информация, тогда как
спектроскопические подходы практически не применяются. О закономерностях тун-
нельного переноса, в том числе о наличии резонансного туннелирования (OMT), как
правило судят по зависимости контраста на СТМ-изображениях от потенциала элек-
трода (рис. 29) [281]. Измерения туннельных спектров в растворе требуют использова-
ния специализированных быстродействующих бипотенциостатов, которые способны
обеспечить необходимый профиль модулирующего напряжения с учетом значительных
токов, связанных с перезаряжением поверхности [282, 283]. Необходимые для интер-
претации экспериментальных спектроскопических данных физические модели, учиты-
вающие наличие молекул воды в туннельном зазоре, существенно более сложны по
сравнению с моделями туннелирования в вакууме [284–289]. И они еще более услож-
няются при появлении в зазоре слоя адсорбированных молекул [289–297]. Среди мо-
дельных гипотез, использующихся для описания процессов туннелирования через ад-
сорбированную молекулу, можно выделить две большие группы: 1) одностадийное ре-
зонансное туннелирование через дискретный уровень молекулы [294, 298] и 2) двух-
стадийное туннелирование в ходе которого происходит полная или частичная колеба-
тельная релаксация молекулы после переноса электрона [290]. В большинстве случаев
однозначный выбор между этими подходами невозможен. Как правило, в in situ конфи-
гурации измеряются только локальные вольтамперные и токвысотные спектры, а более
сложные спектроскопические подходы пока не нашли своего применения.