Добавлен: 06.02.2019
Просмотров: 15913
Скачиваний: 9
56
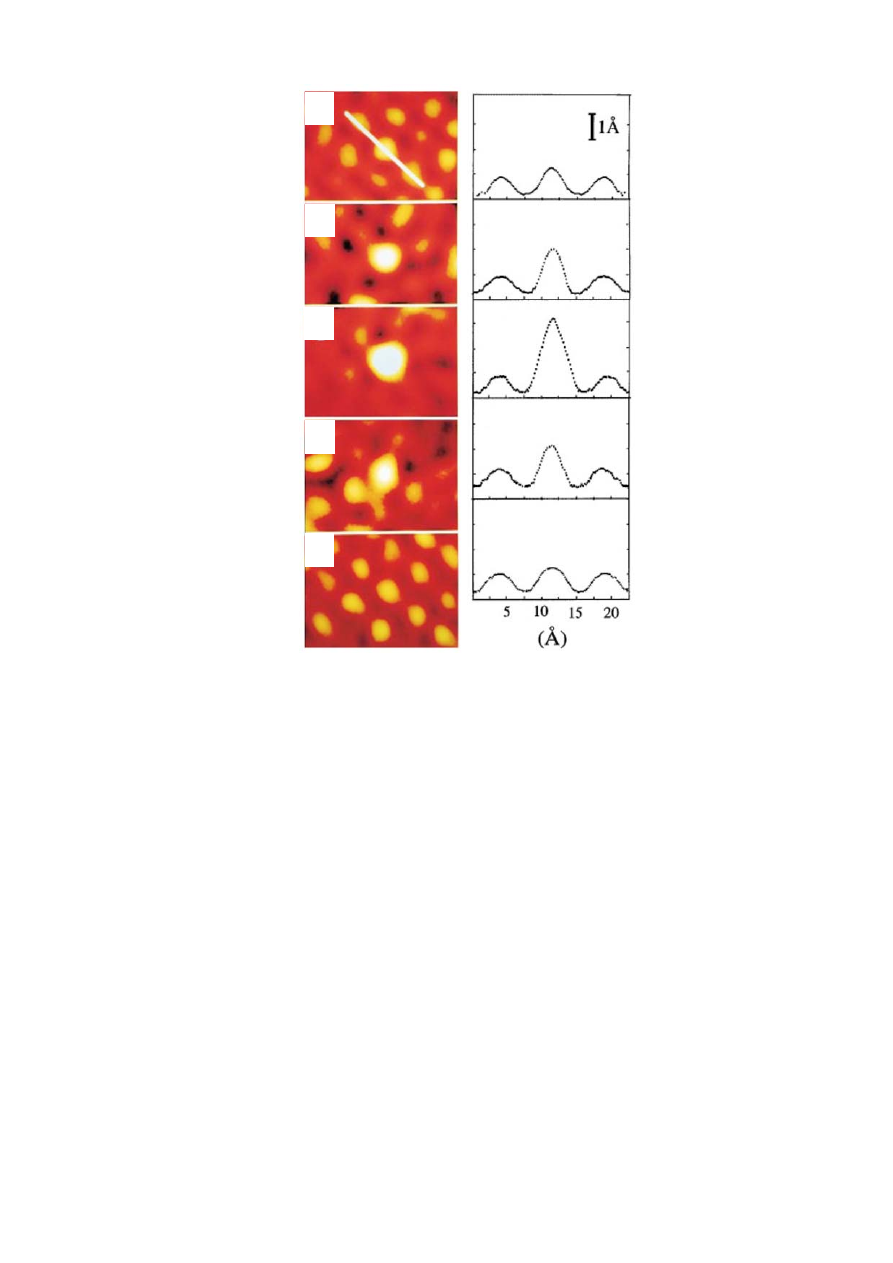
Рис. 29. In situ СТМ-изображения молекулы Fe-протопорфирина в адсорбционном слое
молекул протопорфирина, зарегистрированные при потенциалах –0.15 (а), –0.30 (б),
–0.42 (в), –0.55(г) и –0.65 В(д) относительно насыщенного каломельного электрода
сравнения и отвечающие им сечения [281].
1.2.1. Вольтвысотные зависимости I(U)
Переход от высоковакуумной СТМ-конфигурации к in situ варианту дает возмож-
ность четко контролировать потенциалы электродов и состояние их поверхности. С
другой стороны, в in situ конфигурации туннельное напряжение уже не является неза-
висимо варьируемым параметром. Потенциал образца, потенциал зонда и туннельное
напряжение однозначно связаны соотношением:
tun
sample
tip
U
E
E
=
−
(40)
При этом потенциал образца, как правило, фиксирован, так как он определяет со-
стояние поверхности и, тем самым, строение исследуемых локальных фрагментов на-
ноструктуры. Диапазон изменения потенциала зонда жестко ограничен протеканием на
его поверхности электрохимических процессов с участием материала зонда или компо-
нентов раствора (например, разложение воды), и, как правило, не превышает 1В [282,
283, 299]. Снижение фоновых фарадеевских токов на зонде возможно путем улучшения
а
б
в
г
д
57
качества изоляции его поверхности (уменьшения площади металлической основы, кон-
тактирующей с раствором) и путем тщательной очистки раствора от редокс-активных
примесей, кислорода и т.д. Эти приемы позволяют немного расширить область потен-
циалов, доступную для спектроскопических исследований. Даже в отсутствие фараде-
евских токов эквивалентная схема ячейки микроскопа (рис. 30) включает, помимо ап-
паратной емкости головки, емкость двойного слоя образца и зонда (согласно оценкам
[283], для тщательно изолированного зонда с площадью рабочей поверхности 2•10
-7
см
2
, она составляет около 6 пФ). Перезарядке этих емкостей при высоких скоростях
изменения потенциала могут отвечать токи, значительно превышающие туннельные.
Зависимость туннельного тока от расстояния в растворах существенно более пологая,
чем в высоковакуумной конфигурации (высоты эффективного туннельного барьера не
превышают 1 эВ). Поэтому незначительные различия в структуре адсорбата и природе
материала под зондом (приводящие к локальному изменению
φ) могут приводить к су-
щественному изменению расстояния зонд/образец, отвечающего в разных точках по-
верхности одному и тому же туннельному току. Это также существенно затрудняет
корректное сопоставление локальных вольтамперных зависимостей. Следует отметить,
что, как правило, коммерческие in situ электрохимические ячейки мало пригодны даже
для стандартных топографических исследований, а тем более для туннельно-
спектроскопических (малый объем раствора 100–200 мкл, невозможность измерения
потенциала относительно устойчивого электрода сравнения, заведомо неполное де-
аэрирование раствора и т.д.). В [300] для выделения зависимости туннельного тока от
потенциала на фоне емкостных и фарадеевских токов было предложено вычитать из
кривых, полученных вблизи поверхности образца, кривые, зарегистрированные после
отвода от поверхности на 2–5 нм. Это действительно позволяет несколько уменьшить
вклад осложняющих факторов, однако, как эффективная емкость двойного слоя зонда,
так и величина фарадеевских токов существенно зависят от расстояния зонд-образец
[283], что существенно снижает точность поправки вычитанием. Неоднозначность об-
суждаемой поправки была продемонстрирована и в [300] при анализе зависимости
формы вольтамперной кривой от расстояния, на которое производится отвод зонда от
поверхности. Для снижения емкостного вклада был предложен также импульсный ме-
тод измерения вольтамперных кривых по точкам: после каждого импульса потенциала
(0.3 с), в течение которого измерялась одна пара значений ток/потенциал, петля обрат-
ной связи включалась на 0,3 с для стабилизации зазора [301]. Данный метод неплохо
себя зарекомендовал при исследовании полупроводниковых свойств WSe
2
[301]. В не-
которых случаях, в связи с невозможностью проведения спектроскопических измере-
58
ний в in situ конфигурации, исследователям приходилось, после топографических из-
мерений, извлекать электрод из раствора, высушивать и проводить туннельно-
спектроскопические измерения в ex situ конфигурации [302].
Все вышеперечисленное накладывает жесткие требования как на аппаратное обес-
печение для туннельно-спектроскопических исследований, так и на выбор объекта. По-
этому в литературе присутствует очень ограниченный набор работ [299–313], в кото-
рых производилось измерение вольтамперных зависимостей в in situ условиях, и во
многих случаях их интерпретация оказывалась неоднозначной.
а
б
Рис. 30. Эквивалентная схема измерительной части in situ СТМ (а) и вольтамперо-
граммы Au зонда (б), измеренные в отсутствие туннельного тока в тщательно очи-
щенном от следов кислорода растворе (А и С) при различных скоростях развертки и в
кислород-содержащем растворе (В) [283].
С точки зрения фундаментальных представлений о процессах переноса электрона
в электрохимических системах представляет изучение в in situ конфигурации туннель-
ного переноса с участием дискретных уровней молекулы, локализованной в зазоре.
Теоретические подходы к описанию такого переноса были разработаны Кузнецовым и
Ульструпом [296, 314–325]. Они широко использовались для качественного объяснения
зависимости проводимости туннельного зазора, содержащего адсорбированные моле-
кулы различной природы, от потенциала [281, 297, 326–333] (или напряжения, в случае
измерений в ex situ конфигурации, [334]). При этом далеко не во всех случаях, величи-
ны туннельной проводимости оценивались непосредственно из вольтамперных зависи-
мостей. Так, в [281, 297, 332, 333] для этого использовался анализ зависимости топо-
графического контраста в адсорбированном слое от потенциала (см. рис. 29). Возмож-
59
ность количественной интерпретации экспериментальных данных (и оценки модельных
параметров) была впервые продемонстрирована в [327, 328, 330], а исчерпывающее со-
поставление модельных и экспериментальных результатов было впервые выполнено
на примере N-гексил-N’-(6-тиогексил)-4,4’-бипиридин бромида, адсорбированного на
золоте, в [312].
Схематическая энергетическая диаграмма туннельного зазора в in situ конфигура-
ции представлена на рис. 31. Электронные уровни подложки и зонда непрерывны и по-
ложение их уровня Ферми может независимо варьироваться с помощью бипотенцио-
стата. Туннельное напряжение определяется разностью потенциалов между этими
уровнями (40). Дискретные уровни молекулы в реальной системе значительно размы-
ваются за счет взаимодействия с растворителем и подложкой. Кроме того, положение
уровней флуктуирует около некоторого среднего значения за счет изменения энергии
сольватации (максимальная амплитуда флуктуаций определяется энергией реорганиза-
ции растворителя λ). Вне зависимости от положения электронных уровней молекулы, в
системе протекает некоторый ток, связанный с прямым туннелированием между зон-
дом и подложкой. При изменении потенциала образца, его уровень Ферми приближает-
ся к величинам, отвечающим низшей незаполненной орбитали (LUMO) адсорбата. Ко-
гда за счет флуктуаций положения орбитали уровни выравниваются, становится воз-
можным перенос электрона с подложки на молекулу. В дальнейшем процесс может
развиваться по трем сценариям. 1) Резонансное туннелирование: дальнейший перенос
электрона с молекулы на второй электрод происходит непосредственно после переноса
его на молекулу [294, 297, 298, 335]. 2) В случае слабого электронного перекрывания
между молекулой и электродами, может происходить полная колебательная релаксация
ее состояния, и последующий перенос электрона на второй электрод происходит пол-
ностью независимо [316, 317]. Его возможность определяется взаиморасположением
уровней восстановленной молекулы и зонда. Подобный «поштучный» перенос элек-
трона сквозь молекулу (на единичную флуктуацию положения уровней молекулы пе-
реносится только один электрон) приводит к появлению лишь небольшого дополни-
тельного тока в системе. 3) В случае сильного электронного перекрывания (высокая
скорость электронного переноса), второй перенос электрона с молекулы может проис-
ходить до завершения процесса колебательной релаксации (до того момента, как энер-
гия уже заполненной орбитали понизится ниже уровня Ферми второго электрода). В
ходе обратной релаксации молекулы, уровень LUMO вновь оказывается в ситуации,
когда на него может быть перенесен еще один электрон, и процесс повторяется много-
кратно [314, 318–320]. За счет того, что на каждую первичную флуктуацию положения
60
орбитали происходит перенос большого количества электронов, в системе может на-
блюдаться существенный рост тока. Дальнейшее изменение потенциала образца будет
приводить к стабилизации молекулы в восстановленном состоянии, и исчезновению
дополнительного канала переноса электрона, а, следовательно, снижению тока.
а
б
Рис. 31. Схематическое представление двухступенчатого процесса туннельного переноса с
участием редокс-активной молекулы [312] (а) и схематическая зависимость туннельного
тока от потенциала образца при постоянном туннельном напряжении (б) [327].
На основании модельных представлений [314, 318, 325] для двухступенчатого пе-
реноса электрона с частичной колебательной релаксацией в [312] для фиксированной
геометрии зазора было записано следующее выражение для туннельного тока, текуще-
го через молекулу:
2
1
2
(
)
exp
(
)
2
4
exp
(
)
4
n
M
tun
tun
tun
tun
e
I
e
eU
U
kT
e
U
U
kT
−
⎧
⎡
⎤
ω
⎨
=
ρ
λ+ξη+ γ
+
⎢
⎥
⎣
⎦
π
λ
⎩
⎫
⎡
⎤
⎬
+
λ+
−ξη− γ
⎢
⎥
⎣
⎦
λ
⎭
ы
(41)
где ы — трансмиссионный коэффициент, ρ — плотность электронных состояний ме-
талла вблизи уровня Ферми, ω
n
— характеристическая частота ядерных колебаний,
0
sample
E
E
η=
−
— перенапряжение, ξ и γ — модельные параметры, определяющие за-
висимость эффективного потенциала в точке, отвечающей положению молекулы от пе-
ренапряжения и туннельного напряжения, соответственно (
0
1
≤ ξ ≤ и 0
1
≤ γ ≤ ). Для
ы
= 1 и типичных значений ω
n
для водных растворов и ρ для Au(111), выражение (41)
можно упростить:
2
1
2
9.73
1820
exp
(
)
9.73
exp
(
)
M
tun
tun
tun
tun
I
U
U
U
U
−
⎧
⎡
⎤
⎨
=
λ+ξη+ γ
+
⎢
⎥
⎣
⎦
λ
⎩
⎫
⎡
⎤
⎬
+
λ+
−ξη− γ
⎢
⎥
⎣
⎦
λ
⎭
(42)