Добавлен: 06.02.2019
Просмотров: 15912
Скачиваний: 9
61
где [I
M
] = нА, [λ] = [U
tun
] = [ η ] = В. С учетом (40) в in situ конфигурации независимыми
варьируемыми параметрами, представляющими интерес для исследователя, могут яв-
ляться как туннельное напряжение U
tun
, так и потенциал образца E
sample
. Таким образом,
для сопоставления расчетных и экспериментальных зависимостей могут быть исполь-
зованы два типа вольтамперных спектров: зависимость туннельного тока от U
tun
при
E
sample
=const и зависимость тока от E
sample
при U
tun
=const. При малых перенапряжении и
туннельном напряжении (
tun
U
λ
, η
λ
), выражение (42) упрощается:
910
exp( 9.73(
))
cosh[19.4(
(
0.5)
]
cosh[19.4 (
)]
peak
tun
tun
M
tun
sample
peak
I
U
U
I
U
E
E
−
λ+
=
=
ξη+ γ−
ξ
−
(43)
где cosh( ) [exp( ) exp(
)] / 2
x
x
x
=
+
−
— гиперболический косинус. Величины
910
exp( 9.73(
))
peak
tun
tun
I
U
U
=
−
λ+
(44)
0
(0.5
)
tun
peak
U
E
E
− γ
=
+
ξ
(45)
определяют положение пика туннельной проводимости, а величина
19.4ξ — его шири-
ну (большие значения ξ отвечают более узкому пику). Модель предсказывает (45) ли-
нейную зависимость потенциала пика проводимости от туннельного напряжения с на-
клоном (0.5
) /
− γ ξ и
0
(
0)
peak
tun
E
U
E
= =
. Кроме того, зависимость (44) может быть за-
писана в форме
ln(
/
) (6.81 9.73 ) 9.73
peak
tun
tun
I
U
U
=
−
λ −
(46)
что позволяет определить из экспериментальных данных величину энергии реоргани-
зации λ.
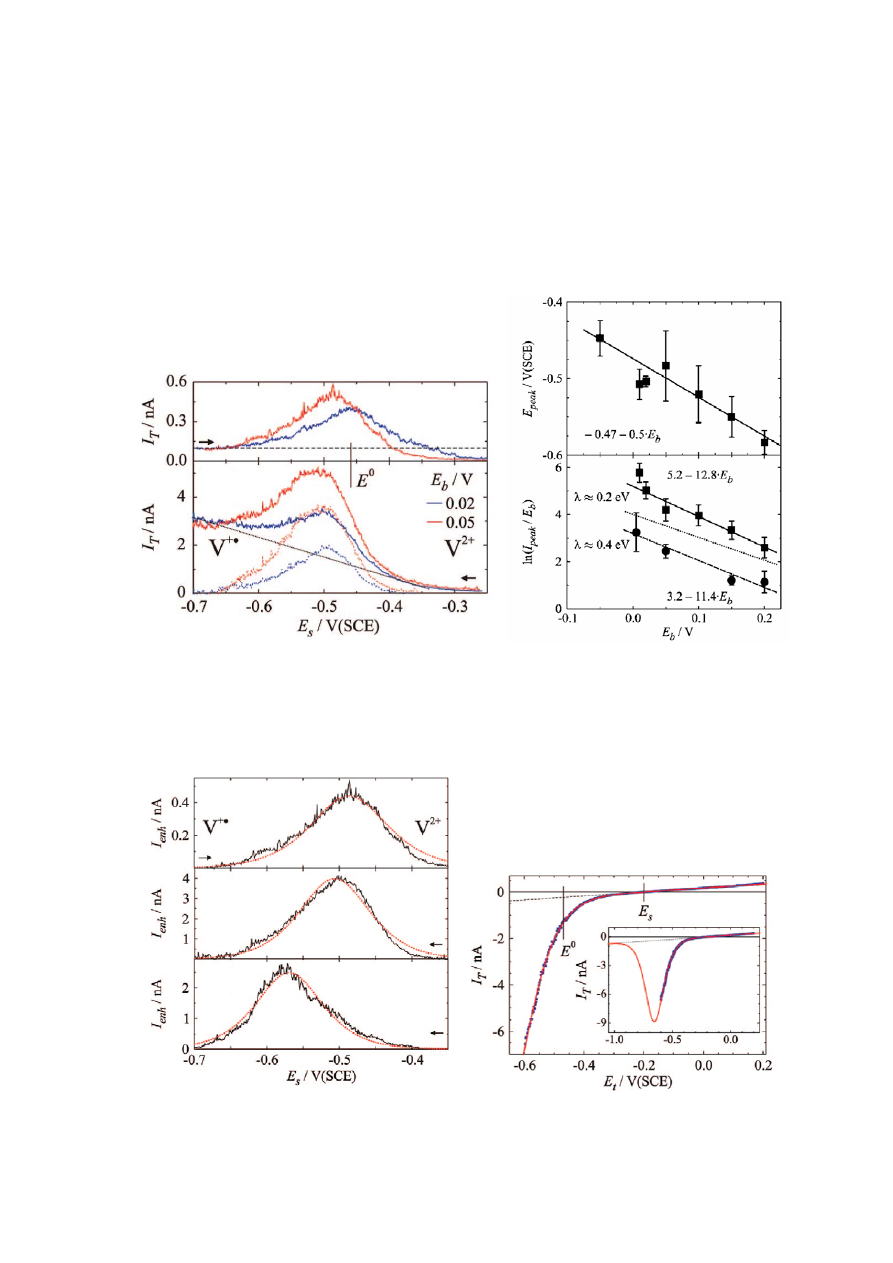
Экспериментальные данные, полученные в [312] для N-гексил-N’-(6-тиогексил)-
4,4’-бипиридин бромида, адсорбированного на золоте, продемонстрировали не только
качественное, но и количественное согласие с представленной моделью (рис. 32). На-
клон полученной зависимости ln(I
peak
/U
tun
) – U
tun
равный 11.4–12.8 неплохо согласуется
с предсказанием модели (9.73). Величина E
0
, определенная из зависимости E
peak
– U
tun
,
равная –0.47В близка к истинному значению (–0.46 В), определенному по электрохи-
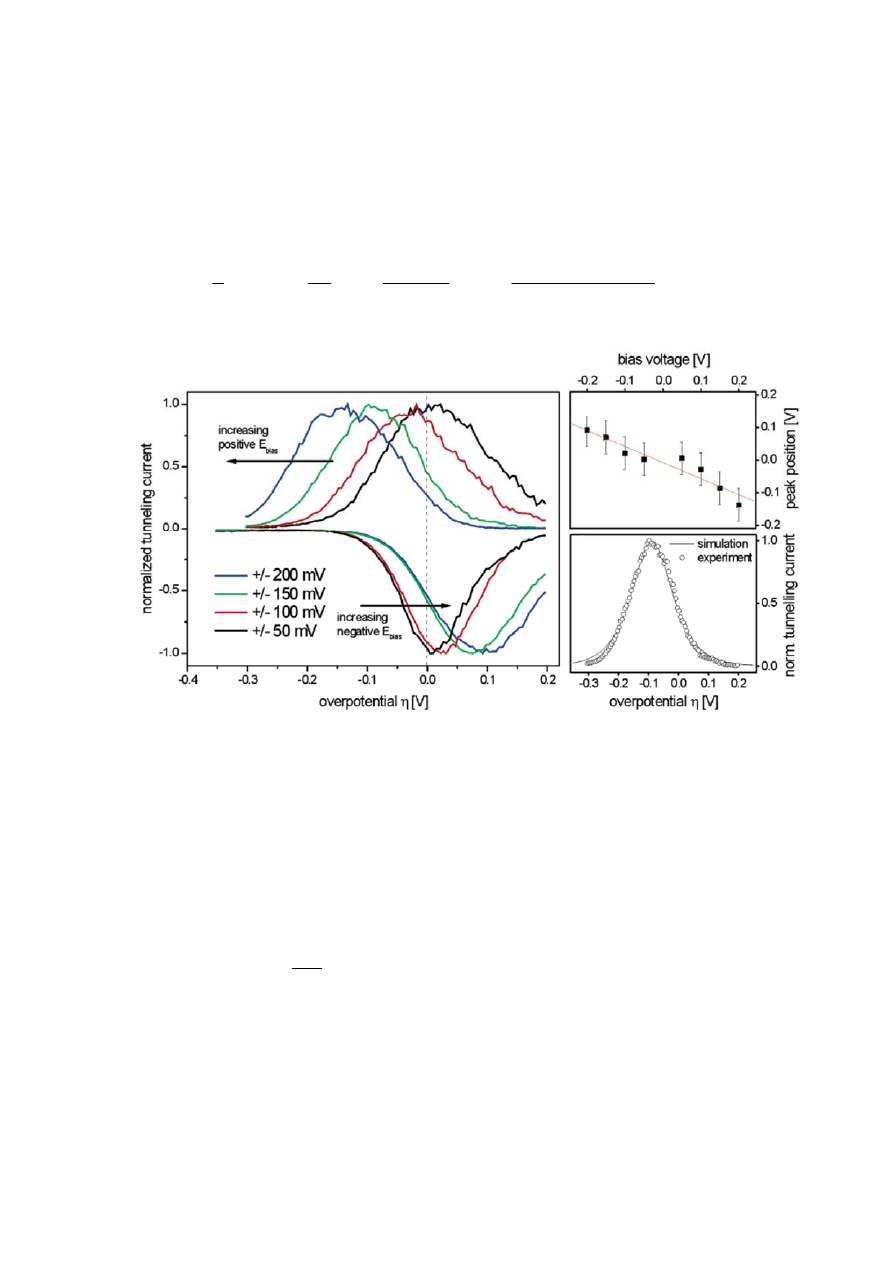
мическим откликам адсорбата. Форма резонансного максимума, также как и «классиче-
ские» вольтамперные кривые, корректно описывается представленной моделью (рис.
33). Величина энергии реорганизации λ, определенная как из линейных зависимостей
рис. 32, так и путем аппроксимации формы пика рис. 33, составила около 0.2 и 0.4 эВ, в
62
зависимости от направления развертки потенциала при измерении вольтамперных кри-
вых (катодном и анодном, соответственно). Так как при различных направлениях раз-
вертки исходная форма адсорбата на поверхности электрода различна (молекула нахо-
дится в окисленной или восстановленной форме), то несовпадение величин λ вполне
закономерно. Значения ξ и γ, определенные из экспериментальных данных были близ-
ки к единице.
а
б
Рис. 32. Экспериментальные зависимости туннельного тока от потенциала образца
(U
tun
=const) измеренные при двух различных направлениях развертки потенциала (а).
Пунктирные кривые получены путем вычитания фоновой составляющей туннельного
тока. Зависимости положения и высоты пика тока от величины туннельного напря-
жения (б) [312].
а
б
Рис. 33. Результаты численной аппроксимации резонансных пиков туннельного тока,
полученных при различных условиях (а) и «классических» вольтамперных зависимо-
стей I
tun
(U
tun
) при E
sample
=const, по уравнению (42) (б)[312].
63
Близкие значения энергии реорганизации (0.3 эВ) и величин ξ и γ (около 1) были
получены для редокс-активного комплекса осмия в [327, 330] на основании анализа
формы резонансного пика тока и зависимости потенциала пика от туннельного напря-
жения (рис. 34). Выражение для тока, протекающего за счет туннелирования с участием
молекулярных орбиталей, записывалось в [327, 330] практически идентично с (41):
1
(0.5
)
1
(
)
exp
cosh
2
2
4
2
n
tun
tun
M
tun
eU
eU
e
I
e
eU
kT
kT
−
⎧
⎫
⎛
⎞
⎡
⎤
ω
λ−
− γ
− ξη
⎨
⎬
=
ρ
−
⎜
⎟
⎢
⎥
⎣
⎦
⎝
⎠
π
⎩
⎭
ы
(47)
Рис. 34. Вольтамперные зависимости I(E
sample
) измеренные при различных туннельных
напряжениях (а). Зависимость положения пика от туннельного напряжения (б) и
модельная аппроксимация формы резонансного пика по уравнению (47) (в). Парамет-
ры модели:
0.3
λ=
эВ,
0.9
ξ =
,
1
γ =
[327].
В случае прямого резонансного туннелирования (в отсутствие колебательной ре-
лаксации молекулы) также должен наблюдаться максимум на зависимости туннельного
тока от потенциала образца [294, 297, 298, 335]. Однако, для этого механизма, положе-
ние максимума резонансного тока [335]:
0
2
tun
peak
U
E
E
=
± λ−
(48)
Таким образом, он должен быть сдвинут относительно потенциала редокс-превращения
молекулы на величину энергии реорганизации λ (рис. 35). Положение пика может слу-
жить качественным критерием, позволяющим сделать выбор между рассмотренными
механизмами. Зависимость плотности состояний молекулы, участвующей в туннельном
переносе, описывается в классическом приближении выражением [335]:
а
б
в
64
2
(
)
( ) exp
4 kT
⎛
⎞
λ−η
ρ η =
−
⎜
⎟
λ
⎝
⎠
(49)
что позволяет оценивать энергию реорганизации среды из экспериментальных данных.
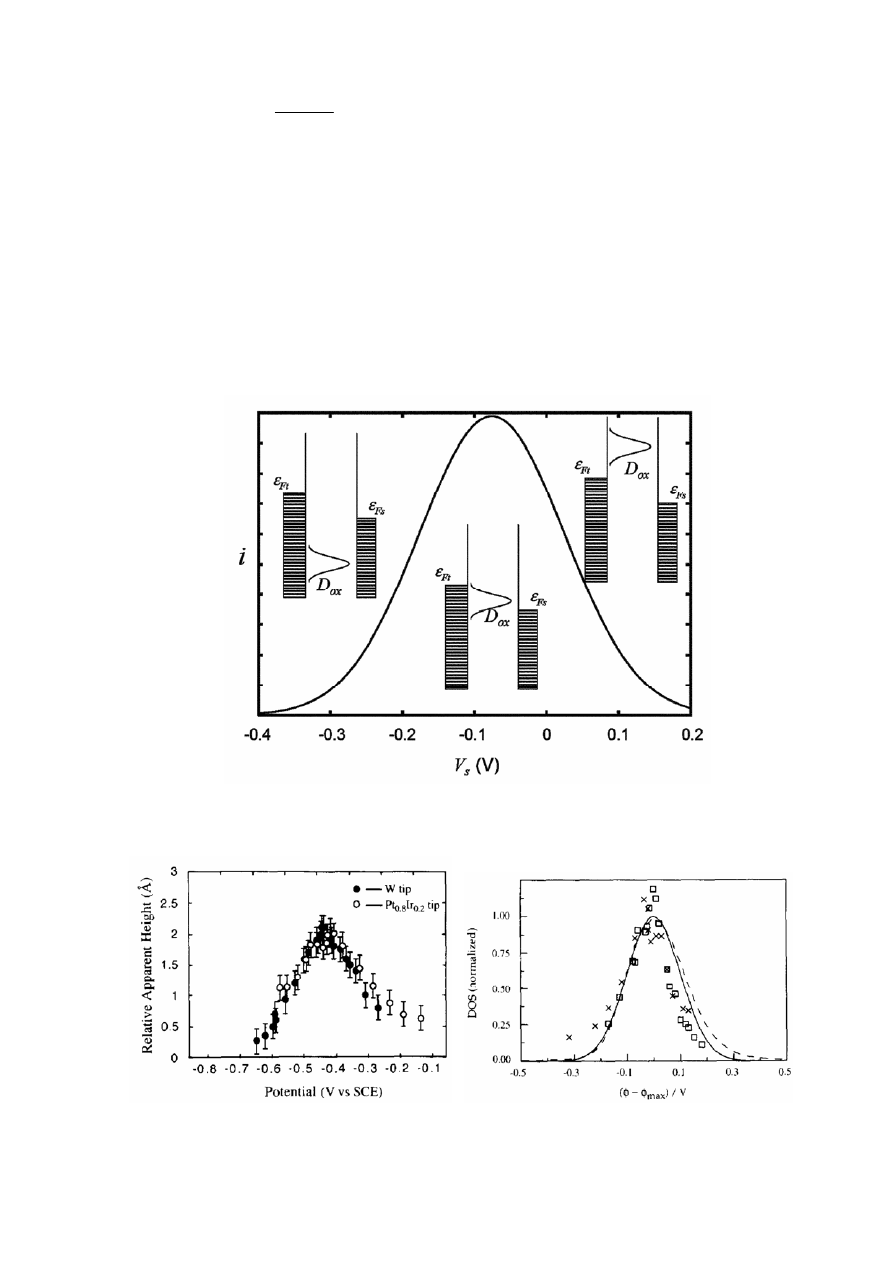
Модель прямого резонансного туннелирования привлекалась, например, для анализа
экспериментальных данных по зависимости топографического контраста молекул Fe-
протопорфирина от потенциала (рис. 36) [281, 335]. В рамках различных модельных
приближений, энергия реорганизации для данной системы была оценена в диапазоне
0.1–0.2 эВ. В то же время, положение максимума проводимости (–0.42 В) существенно
отличалось от предсказаний теории (–0,65 ÷ –0,73В).
Рис. 35. Модельная зависимость туннельного тока от потенциала образца в случае ре-
зонансного туннельного переноса (λ=0.2 эВ, U
tun
=–50 мВ, E
0
=100 мВ). Также показаны
энергетические диаграммы зазора при различных потенциалах [297].
а
б
Рис. 36. Зависимость кажущейся высоты молекулы Fe-протопорфирина в адсорбцион-
ном слое молекул протопорфирина (см. рис. 29) (а) и эффективная плотность состояний
молекулы Fe-протопорфирина, рассчитанная из экспериментальных данных для раз-
ных зондов (б). Сплошная и пунктирная линия — модельные зависимости [335].
65
К механизму резонансного переноса достаточно близок механизм двухстадийного
когереннтного туннелирования, рассматриваемый в [292, 297, 324]. Для данного меха-
низма также можно ожидать смещения положения пика тока относительно потенциала
редокс-превращения молекулы на величину энергии реорганизации [297]:
0
peak
E
E
=
± λ
(50)
Модель [336], предусматривающая резонансный перенос через адсорбированную
молекулу на фоне стохастических флуктуаций энергии системы, предсказывает поло-
жение пика тока при потенциалах близких к E
0
(так же, как и модель двухстадийного
переноса с частичной релаксацией). Однако, математический аппарат, развитый в [336]
не позволяет проводить сопоставления с экспериментальными результатами.
В [297] на основе анализа большого количества литературных данных было пока-
зано, что, по крайней мере, для металлопротеинов, перенос электрона по одностадий-
ному резонансному механизму не наблюдается. Однако, в большинстве случаев, одно-
значный выбор между различными механизмами переноса невозможен. Еще больше
ситуация усложняется в отсутствие потенциостатического контроля. Например, резуль-
таты вольтамперных измерений в мезителене (рис. 37) [303] для различных замещен-
ных порфиринов могут быть объяснены в рамках как одно- так и двухстадийных моде-
лей переноса электрона. Однако и в этом случае, различия в поведении электроактив-
ных и инертных молекул в зазоре очень велики.
а
б
Рис. 37. Вольтамперные (а) и дифференциальные (б) зависимости, зарегистрирован-
ные для различных замещенных порфиринов на золоте в мезителене [303].
В отсутствие редокс-активных ионов в зазоре, картина туннельного переноса
также значительно сложнее, по сравнению с высоковакуумной конфигурацией. Уже в
ходе первых спектроскопических экспериментов (в первую очередь, вольтвысотных,
см. ниже) было показано, что эффективная высота туннельного барьера в растворе зна-
чительно меньше, чем в вакууме, а расстояние между зондом и образцом, значительно
выше. Теоретический анализ в [284] показал, что наличие в зазоре диэлектрической
среды и точечных ионов должно, действительно, приводить к снижению эффективного