Файл: Сканирующая зондовая микроскопия диссертация.pdf

66 

туннельного  барьера,  однако,  это  снижение  не  столь  значительно,  как  наблюдаемое  в 

эксперименте (рис. 38). Аналогичное снижение (примерно до 2 эВ) было предсказано с 

использованием  модели [288], учитывающей  дискретность  распределения  молекул  в 

зазоре,  и  было  показано,  что  профиль  потенциальной  энергии  имеет  минимумы  в  об-

ласти  локализации  атомов  водорода  молекулы  воды.  В  некотором  приближении,  эти 

минимумы могут рассматриваться как локализованные электронные состояния с уров-

нем  энергии  ниже  уровня  Ферми,  а  процесс  туннелирования — как  процесс  переноса 

электрона  через  эти  состояния.  Ранее,  гипотеза  о  преимущественной  ориентации  рас-

творителя в зазоре и появлении областей с локальным положительным зарядом, приво-

дящим к снижению туннельного барьера высказывалась и в [287]. На основании анали-

за экспериментальных вольтамперных и вольтвысотных зависимостей, гипотеза об эс-

тафетном туннелировании электрона в in situ туннельном зазоре была также выдвинута 

в [286, 337]. Согласно этой модели, формирующийся вблизи поверхности зонда и образ-

ца упорядоченный слой диполей воды и ионов формирует промежуточные электронный 

состояния,  через  которые  происходит  эстафетный  туннельный  перенос.  В  этом  случае 

эффективное  расстояние  туннелирования  / (

1)

eff

H

H

n

=

+ ,  а  эффективная  высота  тун-

нельного  барьера 

2

0

/ (

1)

eff

n

φ = φ

+

.  Варьирование  условий  (туннельного  напряжения, 

потенциала  электродов,  расстояния  между  ними)  может  приводить  к  изменению  числа 

промежуточных электронных состояний, что сопровождается появлением скачков и из-

ломов  на  экспериментальных  зависимостях.  Большое  количество  экспериментальных 

данных,  полученных  авторами  (преимущественно  на  электродах  из  платины) (рис. 39) 

хорошо согласовывалось с модельной гипотезой при небольших значениях n. Подробное 

рассмотрение  эффектов,  которые  могут  приводить  как  к  снижению,  так  и  увеличению 

туннельного  барьера  в  растворе  по  сравнению  с  вакуумом  (с  точки  зрения  квантово-

химического моделирования процесса переноса электрона) представлено в [289]. 

а

 б

Рис. 38. Зависимость туннельной проводимости (а) и эффективной высоты туннельно-

го барьера (б) от расстояния для туннелирования в вакууме (квадраты) и в растворе 

(кружки) в рамках модели [284]. 

67 

а

 б

Рис. 39. Зависимость эффективной высоты туннельного барьера от потенциала образ-

ца (а) и статистика высот барьера, при которых происходит его скачкообразное изме-

нение на 

eff

sample

E

φ −

 зависимости (б) [337]. 

Наиболее  типичная  постановка  работ  в  области  in situ  туннельной  спектроскопии 

посвящены  проблеме  молекулярной  электроники  (исследованиям  отрицательного  диф-

ференциального сопротивления, проводимости индивидуальной молекулы [307, 308, 310, 

311, 313, 327, 331, 334, 338–340]), и, как правило, также тесно связана с проблемой тун-

нелирования с участием молекулярных орбиталей. В [304] было выявлено значительное 

увеличение  амплитуды  осцилляций  тока  на  вольтамперограммах  измереных  над  элек-

троосажденным нанокластером меди. Небольшое количество вольтамперных измерений 

проводилось также в ионных жидкостях [309, 329]. В том числе, в [329] были продемон-

стрированы  эффекты  резонансного  туннелирования  через  молекулярную  орбиталь  для 

редокс-активного комплекса осмия в 1-бутил-3-метилимидазолий гексафторфосфате. 

В растворе, как и в вакууме, для полупроводниковых материалов удается наблю-

дать закономерности, характерные для туннелирования в MIS конфигурации [300, 301, 

306]. При этом анализ зависимости формы вольтамперной зависимости от расстояния 

зонд/образец может в некоторых случаях позволить разделить вклад туннельного барь-

ера и барьера, формирующегося вследствие формирования обедненной зоны в поверх-

ностных слоях полупроводника.  

Зонд туннельного микроскопа также может быть использован для создания непо-

средственного контакта атомарных размеров с наноструктурой, сформированной путем 

электроосаждения в растворе [282, 299, 305]. При этом становятся возможны измерения 

свойств  гетероконтакта  наноструктура/подложка,  что  и  было  продемонстрировано  на 

примере гетероструктуры n-Si(111)/нанокластер Au [305]. Для нее было зафиксировано 

существенное снижение высоты барьера Шоттки и, следовательно, увеличение рабочей 

плотности тока, по сравнению найденными ранее для объемных осадков золота.  

68 

1.2.2. Токвысотные зависимости I(H) 

Измерения  токвысотных  зависимостей  в  in situ  конфигурации  сопряжены  менее 

серьезными  методическими  трудностями,  чем  измерения  вольтамперных  кривых.  По-

этому  на  этапе  становления  in situ  туннельной  микроскопии  этот  метод  активно  ис-

пользовался для анализа природы процессов, обеспечивающих протекание тока между 

зондом и образцом [286, 337, 341–349]. Оценки эффективной высоты туннельного барь-

ера,  приводившие  к  существенно  более  низким  величинам,  чем  в  высоковакуумной 

конфигурации, редко превышают 1 эВ (лишь в [342, 343, 345] были получены значения 

1–2  эВ).  Отклонения  от  экспоненциальной  зависимости  тока  от  расстояния,  выражен-

ная  зависимость  высоты  барьера  от  потенциала  стимулировали  развитие  модельных 

представлений  о  процессах  туннелирования  с  участием  молекул  растворителя,  кратко 

рассмотренных  выше [284–287]. Снижение  эффективной  высоты  барьера  приводит  к 

увеличению  равновесного  расстояния  между  зондом  и  образцом.  Согласно  оценкам 

[346],  оно  составляет  не  менее 2 нм  при  сопротивлении  зазора  1ГОм,  а  иногда  непо-

средственного  механического  контакта  между  зондом  и  образцом  не  удается  достичь 

даже при приближении к поверхности на 4 нм.  

В  дальнейшем,  традиционное  использование  данного  метода  для  определения 

эффективной высоты туннельного барьера и, тем самым, механизма туннельного пере-

носа, не нашло в in situ конфигурации широкого применения. Этот метод оказался го-

раздо  более  востребован  для  изучения  молекулярной  проводимости  индивидуальных 

молекул [340, 350–353], структуры растворителя и адсорбционных слоев на поверхно-

сти электродов [354–357], фазовых пассивирующих слоев [358]. 

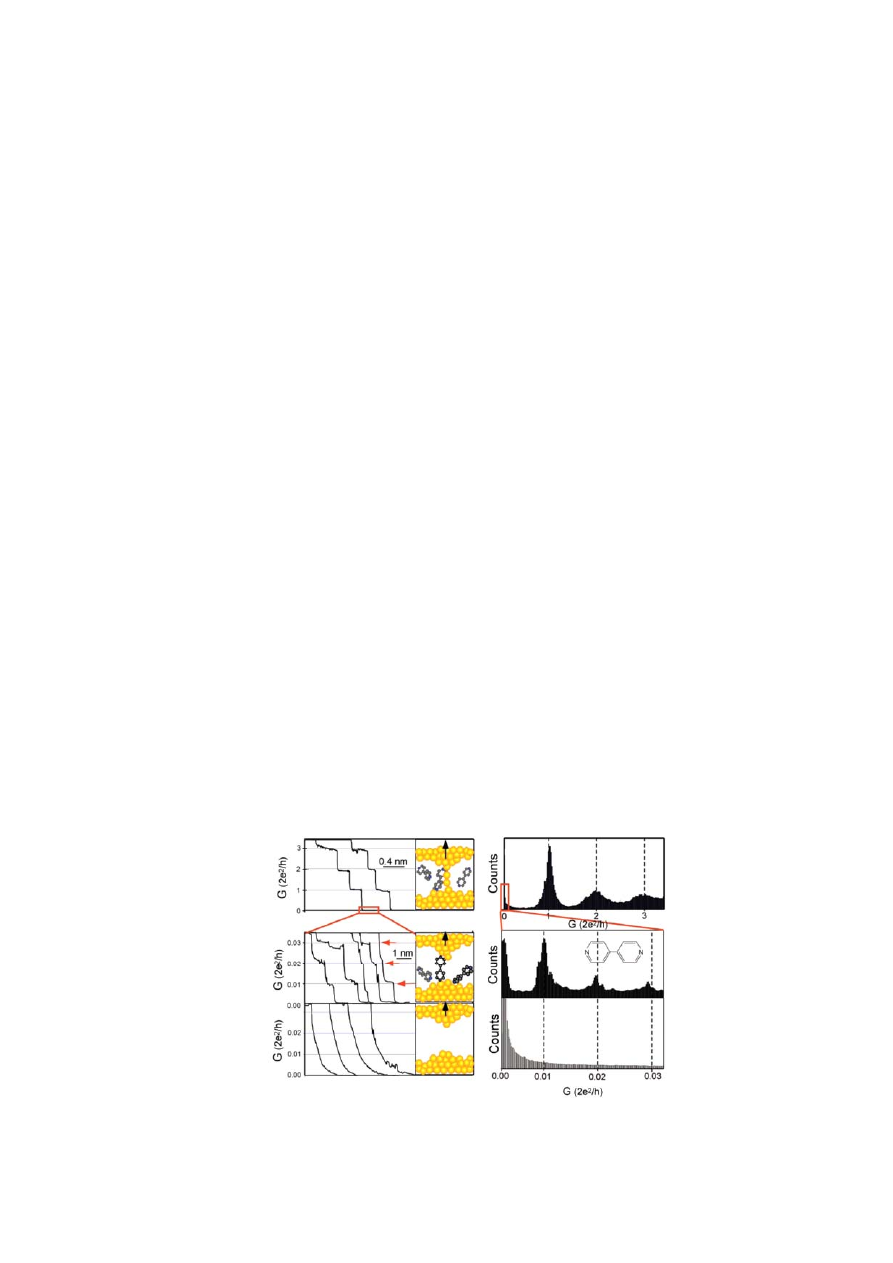
В  основе  метода  изучения  сопротивления  индивидуальных  молекул  лежит  кван-

тование проводимости туннельного зазора при образовании молекулярных «мостиков» 

между  зондом  и  образцом [350] (рис. 40). После  введения  зонда  в  непосредственный 

механический  контакт  с  подложкой  и  его  оттягивании  от  поверхности,  проводимость 

формирующегося  мостика  из  атомов  металла  (нанонити)  квантуется  с  фундаменталь-

ной  дискретностью  G

0

=2e

2

/h  (рис. 40а).  При  наличии  в  растворе  или  на  поверхности 

молекул, способных образовывать прочные связи с материалом зонда и образца (обыч-

но используются молекулы, содержащие тиольные группы и золотые электроды), воз-

можно образование мостиковых связей (рис. 40в). При поочередном разрушении мос-

тиков, по мере увеличения расстояния зонд/образец, вновь происходит дискретное из-

менение  проводимости.  Статистический  анализ  большого  числа  токвысотных  кривых 

позволяет  точно  установить  величину  ступени,  отвечающей  проводимости  индивиду-

альной молекулы. Оценки молекулярной проводимости могут быть также получены из 

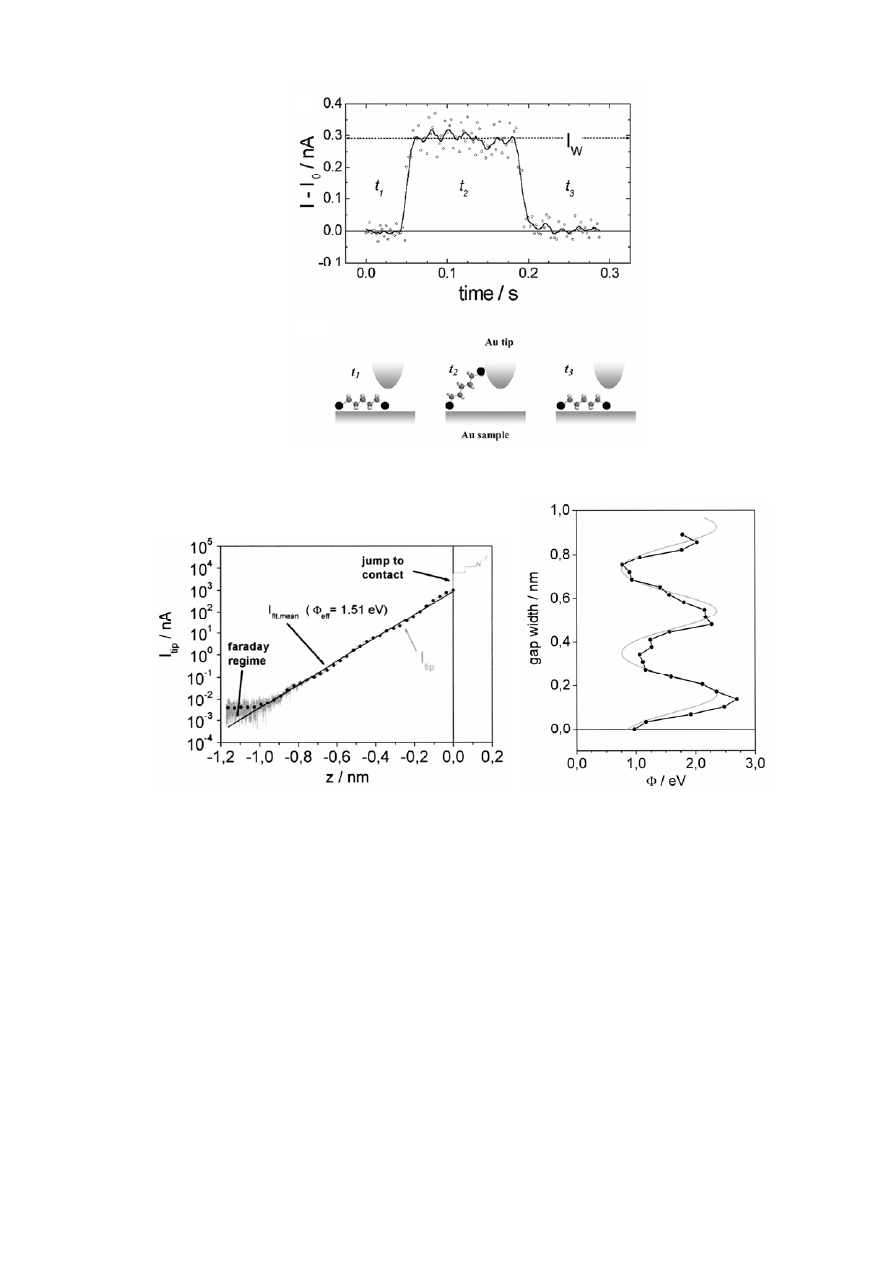
69 

анализа  флуктуаций  тока  на  I(t)  зависимостях  при  фиксированном  положении  зонда 

(рис. 41) [351]. В ряде случаев этот подход обеспечивает лучшую точность, чем анализ 

токвысотных  зависимостей.  В  тех  случаях,  когда  в  молекуле  отсутствуют  функцио-

нальные  группы,  обеспечивающие  образование  «мостиков»,  величина  молекулярной 

проводимости может быть получена путем анализ изменения наклона токвысотной за-

висимости при переходе (по мере приближения зонда к поверхности) от режима тунне-

лирования  сквозь  молекулярный  слой  (подложка/адсорбат/диэлектрик/зонд)  к  непо-

средственному  контакту  зонда  с  адсорбатом  (подложка/адсорбат/зонд)  и,  в  последую-

щем, к механическому контакту с подложкой [353]. Аналогичный подход реализуется и 

при анализе структуры ионных адсорбатов и структуры растворителя [354–357] (осно-

вы этого подхода были заложены в [347, 348]). При анализе зависимости эффективной 

высоты туннельного барьера от расстояния до поверхности в [354, 355] было выявлено 

его осциллирующее поведение (рис. 42) с периодом, близким к размеру молекулы во-

ды. Ранее признаки подобного осциллирующего поведения на I(H)-зависимостях были 

обнаружены в [348]. Формирование упорядоченной структуры воды вблизи поверхности 

электрода было доказано методом рентгеновского рассеяния [359], а дискретное измене-

ние проводимости в туннельном зазоре, сформированном из двух ртутных капель, было 

впервые обнаружено в [360]. Аналогичные подходы были использованы в [356, 357] для 

анализа  электронной  структуры  двойного  электрического  слоя  на Au(111) электроде  и 

адсорбатов, содержащих сульфат, хлорид-ионы и ионы меди. В этих работах для извле-

чения  информации  о  высоте  туннельного  барьера  использован  не  анализ  зависимости 

d ln / d

I

H

, а аппроксимацию экспериментальной кривой в предположении о туннелиро-

вании  через  последовательный  набор  туннельных  барьеров,  с  дискретностью,  равной 

дискретности изменения положения зонда в ходе измерений, в рамках модели [361].  

Рис. 40. Токвысотная зависимость (а) и соответствующая гистограмма проводимости 

(б) для проводящего мостика из атомов металла, сформированного при контакте меж-

ду зондом и образцом. Токвысотные зависимости в присутствии (в) и в отсутствие (д) 

молекул в зазоре и отвечающие им гистограммы проводимости (г, е) [350]. 

а 

б 

в 

г 

д 

е 

70 

Рис. 41. Флуктуация туннельного тока (а) и схематическое изображение туннельного 

зазора (б) для образца Au(111), покрытого 1,8-октандитиола [351].  

а

 б

Рис. 42. In situ токвысотная зависимость, зарегистрированная для Au(111) в 0.02M 

HClO

4

 (a), и зависимость высоты эффективного туннельного барьера от расстояния до 

поверхности (б) [355].  

1.3. Особенности строения «туннельного» зазора  

при измерениях в ex situ конфигурации 

Метод сканирующей туннельной микроскопии в ex situ конфигурации использу-

ется значительно более широко, по сравнению с in situ конфигурацией. Адаптация ме-

тода для измерений на воздухе позволила значительно упростить и удешевить прибор, 

что  способствовало  массовому  распространению  СТМ.  Первое  СТМ-изображение  с 

атомарным разрешением на воздухе было получено уже в 1986 г. [362]. Тем не менее, 

практически сразу стало очевидно, что условия переноса электрона в этой конфигура-

ции  существенно  иные,  чем  в  вакууме,  из-за  присутствия  в  зазоре  СТМ  примесей 

а 

б