ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 28
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
У. Джонсон [98], исследуя коррозию алюминия в водопроводной воде, установил, что развитие питтинга (точечной коррозии) после инкубационного периода происходит по закону
который в точности совпадает с уравнением (7.5). Процесс окисления никельхромовых сплавов протекает по более сложному закону, зависящему от температуры и типа сплава. На первой стадии кинетика окисления подчиняется логарифмическому закону:
а затем закону
В этих выражениях ^ ,к2 ,к, п - постоянные величины, определяемые на основании опытных данных.
Анализируя приведенные выше математические модели коррозионного процесса можно отметить, что при их построении авторы идут двумя путями. Первый состоит в учете многочисленных внешних воздействий, вызывающих коррозию металла, и выявлении степени влияния каждого фактора на процесс коррозии экспериментальным путем. Второй путь заключается в разработке математической модели коррозионного процесса в виде функционального или дифференциального уравнения, по возможности более или менее точно аппроксимирующего реальную кинетику коррозионного разрушения.
Координата фронта диффузии продукта метаболизма в композит может быть оценена по формуле
где К(<^) - коэффициент, зависящий от изменения концентрации среды по толщине изделия, ? = 1 - c(x,t) С0
Если некоторые компоненты материала являются источниками питания микроорганизмов, то

п - концентрация веществ, усваиваемых микроорганизмами, Кх - константа скорости взаимодействия веществ.
Диффузионная модель деградации характерна для полимерных композитов. В экспериментах использованы карбамидные, эпоксидные, полиэфирные композиты. Агрессивная среда - это 10% серная кислота и вода. Выдержка - 90 суток.
Изменение модуля упругости может быть описано степенной зависимостью.

при полном разрушении материала на поверхности
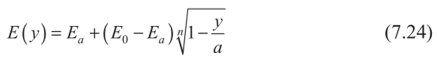
здесь awn — определяются из эксперимента.
Таким образом, при математическом моделировании можно использовать модели поверхностного разрушения материала конструкции, причем из-за отсутствия экспериментальных данных, приходится считать, что скорость коррозионного разрушения не зависит от величины и вида напряженного состояния.
Сравнивая описанные выше модели коррозии можно заметить, что для описания процессов коррозионного повреждения в различных средах используются нередко похожие или даже совпадающие математические модели. Экспериментальные данные, полученные в натурных и лабораторных условиях, и расчеты, проведенные Л. Я. Цикерманом, подтверждают, что процесс коррозионного разрушения металлов в различных средах (грунте, атмосфере, морской и пресной воде, зонах периодического увлажнения, атмосфере промышленных предприятий), а также разрушение стальной арматуры в бетоне феноменологически сходны. Поэтому он предлагает описывать процесс коррозионного поражения различных металлов в разных агрессивных средах общей математической моделью либо в виде дробно-линейной функции

либо в виде экспоненциальной зависимости
Графики этих функций приведены на рис. 7.2 (кривая 2). Экспериментальную кривую 1, полученную Л. Я. Цикерманом, можно разбить на два участка: первый - до точки перегиба и второй - после точки перегиба. На первом участке наблюдается интенсивное увеличение скорости коррозии, сопровождающееся большими потерями металла, на втором коррозия затухает. Это объясняется тем, что продукты коррозии, закрывая поверхность металла, уменьшают контакт его с агрессивной средой и тем самым способствуют замедлению процесса коррозионного разрушения.
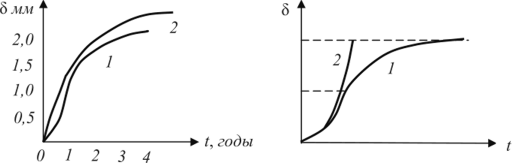
Рис. 7.2
Сопоставление теоретических кривых с экспериментальной кривой позволяет отметить, что функции (7.25) и (7.26) удовлетворительно описывают экспериментальную кривую за точкой перегиба, но качественно неверно описывают коррозионный процесс на первом участке, так как они в состоянии описывать только процесс с уменьшающейся с течением времени скоростью. На правом рисунке
(рис. 7.2) показана экспонента I и логистическая кривая 2, которая соответствует экспериментальной кривой.
Для преодоления указанных затруднений Л .Я. Цикерман предложил модель коррозионного процесса в виде дифференциального уравнения второго порядка:
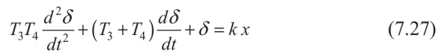
где Г, и Т4 — параметры коррозионного процесса; к - так называемый коэффициент передачи; х - характеристика агрессивных свойств внешней среды, с которой контактирует металл. Решение этого уравнения имеет вид
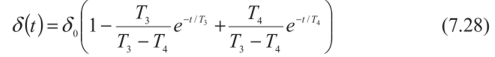
Характер этой кривой соответствует экспериментальной кривой (рис. 7.2), однако пользоваться этой зависимостью трудно ввиду ее сложности. Кроме того, функция (7.28) является решением линейного уравнения (7.27), которое нелинейный процесс коррозионного разрушения описывает приближенно.
Для описания процесса коррозионного разрушения во времени построим математическую модель в виде нелинейного дифференциального уравнения. Процесс коррозионного разрушения на начальном его этапе (до точки перегиба, рис. 7.2) опишем дифференциальным уравнением
где к - постоянная величина, характеризующая отклик на глубину коррозионного разрушения. Это уравнение показывает, что скорость роста слоя,
пораженного коррозией —, пропорциональна достигнутой глубине S,
dt
1 dS
или относительная скорость коррозии--остается постоянной величи-
5 dt
ной. Решая (7.29), получаем уравнение экспоненты
соответствующей начальному участку кривой.
Механизм коррозионного разрушения, заданный уравнением (7.29), сохраняется до точки перегиба, а затем должны проявить себя сдерживающие факторы из-за уменьшения контакта металла с агрессивной средой вследствие защитного действия продуктов коррозии. В этом случае проким образом, чем больше глубина коррозии, тем меньше скорость ее нарастания.
Решение дифференциального уравнения (7.32) имеет вид

цесс коррозионного разрушения можно представить дифференциальным уравнением
в котором рост коррозии ограничен; S0 - максимальная глубина коррозии. Относительная скорость коррозии
линейно убывает с ростом 8 - глубины коррозии (00,?>0). Таи называется логистической кривой Ферхюльста. Графическое изображение ее приведено на рис. 7.2. В начальные моменты времени, когда 8<8п, логистическая кривая совпадает с экспонентой. Прямые 8 = 80 и 8 = 0 являются асимптотами логистической кривой. При 8 = 80 /2 логистическая кривая имеет точку перегиба, в которой меняется знак ускорения.
Логистическая кривая дает хорошие результаты в математической статистике при описании роста какой-либо совокупности - клеток, людей, популяции животных, эпидемий. Можно предполагать, что она позволит достаточно точно описать такой распространенный процесс, как коррозионное разрушение.
Таким образом, применение рассмотренных выше моделей поверхностного разрушения материала конструкций приводит к следующему алгоритму.
-
1. Выполняем расчет конструкции и определяем ее размеры, обеспечивающие заданные критерии прочности и деформативности. -
2. В соответствии с применяемым материалом и видом агрессивной среды берем одну из рассмотренных выше моделей или выбираем подходящую модель в справочной литературе и задаем время надежной эксплуатации конструкции (долговечность). -
3. По заданной долговечности вычисляем толщину пораженного коррозией слоя и добавляем ее к размерам конструкции, определенным в первом пункте. -
4. Для определения запаса прочности конструкции определяем толщину слоя поврежденного коррозией в соответствии с выбранной моделью и известному времени эксплуатации конструкции в агрессивной среде. Определяем текущие размеры конструкции. Далее производится поверочный расчет конструкции с текущими размерами и делается заключение о соответствии его НДС прочностным и деформационным критериям.
В описанных выше математических моделях влияние напряженно- деформированного состояния на процесс коррозионного разрушения не учитывалось. Однако это влияние во многих случаях может оказаться столь значительным, что им нельзя пренебрегать.
Впервые влияние напряжений на скорость коррозии в расчетах на прочность было учтено В.М. Долинским. Величина скорости коррозии в первых работах В.М. Долинского считалась линейной функцией абсолютной величины напряжений. В последующих его работах скорость коррозии принималась в виде линейной функции интенсивности напряжений <т.
где У0 - скорость коррозионного разрушения ненапряженного элемента; m - коэффициент, учитывающий влияние напряженного состояния на скорость коррозии.
Глубина разрушаемого слоя элемента конструкции с учетом уравнения (7.34) определится следующим образом:
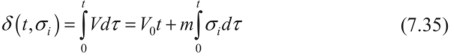
В.Г. Карпунин [99] предложил модель коррозионного разрушения в виде дифференциального уравнения первого порядка
с начальным условием J(x,^,0) = 0. Здесь х, у — координаты точек поверхности рассматриваемого элемента конструкции;/- функция, учитывающая влияние времени коррозионного процесса и уровня действующих напряжений; а <7 - некоторая функция, характеризующая напряженное состояние в точке разрушаемой поверхности элемента конструкции. Вид функции f(t,cr) принимается на основе экспериментальных данных. При построении этой функции предлагается представлять ее в виде произведения двух функций, одна из которых зависит только от времени t, а другая является линейной функцией интенсивности напряжений сг, например
Вид безразмерной функции (p{t), а также значения коэффициентов a,j3 находятся экспериментальным путем, причем функцию
можно приближенно задавать в виде
Очевидно, что модель (7.37) допускает обобщение. Например, можно принять:
где п - также определяется экспериментальным путем. Используя эту модель, В.Г. Карпунин выполнил исследование прочности и устойчивости пластинок и оболочек с учетом коррозионного износа.