Файл: Лекция Геометрические характеристики плоских сечений.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 66
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(12)
Оси называются центральными, если они проходят через центр тяжести фигуры, т. е. статические моменты относительно этих осей равны нулю. Главными осями инерции фигуры называются оси относительно которых центробежный момент инерции равен нулю. Если фигура имеет хотя бы одну ось симметрии, то эта ось является главной осью.
Определим осевые моменты инерции прямоугольника относительно осей x и y , проходящих через его центр тяжести (рис. 4.6). В качестве элементарной площадки dА возьмем полоску шириной b и высотой dy (рис. 4.4). Тогда будем иметь:
Аналогичным образом можно установить, что
.
Центробежный момент инерции сечения относительно осей, хотя бы одна из которых является осью симметрии, равен нулю.
Для систем, рассматриваемых в полярной системе координат (рис. 4.7, а), вводится также полярный момент инерции:
.
где
- радиус-вектор точки тела в заданной полярной системе координат.
Рис. 4.7
Вычислим полярный момент инерции круга радиуса R. На рис. 4.7, a показана элементарная площадка, очерченная двумя радиусами и двумя концентрическими поверхностями, площадью
.
Интегрирование по площади заменим двойным интегрированием:
.
Hайдем зависимость между полярным и осевыми моментами инерции для круга. Из геометрии видно (рис. 4.7, б), что
,
следовательно,
.
Так как оси x и y для круга равнозначны, то
.
Полярный момент инерции кольца может быть найден как разность моментов инерции двух кругов: наружного (радиусом R) и внутреннего (радиусом r):
.
Размерность моментов инерции L4. Осевые и полярные моменты инерции всегда положительны, центробежный момент инерции может быть положительным, отрицательным, равным нулю.
Для фигур, имеющих более двух осей симметрии, осевые моменты инерции относительно всех центральных осей равны между собой. К таким фигурам относятся равносторонний треугольник, квадрат, круг и т.д.
Моменты инерции простых сечений
Вычислим моменты инерции простейших фигур.
Прямоугольник
Определим моменты инерции относительно осей, совпадающих со сторонами, и относительно центральных осей.
По определению
.
Рис. 4.8
Элемент площади равен dA = bdy,
следовательно
.
По формуле
, откуда, учитывая что А = bh, yc = 0,5h, находим
.
Аналогично получим
и 
.
Треугольник
Момент инерции относительно оси х, cовпадающей с основанием,
.
Но dA = b(y)dy, b(y) = (b/h)(h-y).
Cледовательно,
.
Рис. 4.9
По формуле параллельного переноса
, откуда 
.
Круг
Для любых центральных осей
, поэтому 
.
Как известно, полярный момент инерции круга равен
.
Рис. 4.10
Следовательно,
.
Кольцо (
).
Момент инерции относительно оси
(рис.4.11) можно определить как разность моментов инерции наружного и внутреннего круга:
.
Для тонкого кольца существует приближенная формула
, где dср – средний диаметр, t - толщина кольца.
Рис. 4.11
Моменты инерции сечений сложной формы
Момент инерции сечения сложной формы относительно некоторой оси равен сумме моментов инерций его составных частей относительно той же оси:
, (13)
что непосредственно следует из свойств определенного интеграла. Таким образом, для вычисления момента инерции сложной фигуры надо разбить ее на ряд простых фигур, вычислить моменты инерции этих фигур, а затем просуммировать их.
Пример 3.
Определить момент инерции сечения, показанного на рис. 4.12, относительно оси симметрии, a=10 см.
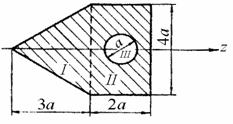
Рис.4.12
Решение.
Разбиваем заданное сечение на простейшие элементы: I - Равнобедренный треугольник, II - прямоугольник, III - круг.
Момент инерции сложной фигуры относительно оси z согласно формуле (13):
.
Определяем моменты инерции слагаемых простейших элементов:
Для равнобедренного треугольника:
;
для прямоугольника согласно формуле:
;
для круга согласно формуле:
.
Окончательно получим:
Iz=4,0a4+10,67a4-0,0491a4=14,6a4=14,6×104=1,46×105 см4.
Пример 4.
Определить момент инерции симметричного сечения, показанного на рис. 4.13, относительно вертикальной оси симметрии y. Двутавр №10 (ГОСТ 8239-56). Швеллер №5 (ГОСТ 8240-56).
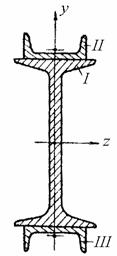
Рис.4.13
Решение.
Разбиваем исходное сечение на простейшие элементы, моменты инерций которых приводятся в справочниках: I - двутавр, II и III - швеллеры.
По сортаменту на стандартные прокатные профили имеем:
Для двутавра №10 (ГОСТ 8239-56): H=10 см, B=7 см, F=14,2 см2, Ix=244 см4, Iy=35,3 см4.
Для швеллера №5 (ГОСТ 8240-56): h=5 см, b=3,7 см, F=6,90 см2, Ix=26,1 см4, Iy=8,41 см4, x0=1,35 см.
Момент инерции сечения относительно оси y согласно (13)
т.к. оба швеллера расположены идентично относительно оси y.
Для двутавра
.
Для швеллера
сортам.=26,1 см4.
Окончательно имеем:
Оси называются центральными, если они проходят через центр тяжести фигуры, т. е. статические моменты относительно этих осей равны нулю. Главными осями инерции фигуры называются оси относительно которых центробежный момент инерции равен нулю. Если фигура имеет хотя бы одну ось симметрии, то эта ось является главной осью.
Определим осевые моменты инерции прямоугольника относительно осей x и y , проходящих через его центр тяжести (рис. 4.6). В качестве элементарной площадки dА возьмем полоску шириной b и высотой dy (рис. 4.4). Тогда будем иметь:
Аналогичным образом можно установить, что
.Центробежный момент инерции сечения относительно осей, хотя бы одна из которых является осью симметрии, равен нулю.
Для систем, рассматриваемых в полярной системе координат (рис. 4.7, а), вводится также полярный момент инерции:
.где
- радиус-вектор точки тела в заданной полярной системе координат. Рис. 4.7
Вычислим полярный момент инерции круга радиуса R. На рис. 4.7, a показана элементарная площадка, очерченная двумя радиусами и двумя концентрическими поверхностями, площадью
.Интегрирование по площади заменим двойным интегрированием:
.Hайдем зависимость между полярным и осевыми моментами инерции для круга. Из геометрии видно (рис. 4.7, б), что
,следовательно,
.Так как оси x и y для круга равнозначны, то
.
Полярный момент инерции кольца может быть найден как разность моментов инерции двух кругов: наружного (радиусом R) и внутреннего (радиусом r):
.Размерность моментов инерции L4. Осевые и полярные моменты инерции всегда положительны, центробежный момент инерции может быть положительным, отрицательным, равным нулю.
Для фигур, имеющих более двух осей симметрии, осевые моменты инерции относительно всех центральных осей равны между собой. К таким фигурам относятся равносторонний треугольник, квадрат, круг и т.д.
Моменты инерции простых сечений
Вычислим моменты инерции простейших фигур.
Прямоугольник
Определим моменты инерции относительно осей, совпадающих со сторонами, и относительно центральных осей.
По определению
. Рис. 4.8
Элемент площади равен dA = bdy,
следовательно
.По формуле
, откуда, учитывая что А = bh, yc = 0,5h, находим .Аналогично получим
и .Треугольник
Момент инерции относительно оси х, cовпадающей с основанием,
.Но dA = b(y)dy, b(y) = (b/h)(h-y).
Cледовательно,
.
Рис. 4.9
По формуле параллельного переноса
, откуда .Круг
Для любых центральных осей
, поэтому .Как известно, полярный момент инерции круга равен
. Рис. 4.10
Следовательно,
.Кольцо (
).Момент инерции относительно оси
(рис.4.11) можно определить как разность моментов инерции наружного и внутреннего круга: .Для тонкого кольца существует приближенная формула
, где dср – средний диаметр, t - толщина кольца. Рис. 4.11
Моменты инерции сечений сложной формы
Момент инерции сечения сложной формы относительно некоторой оси равен сумме моментов инерций его составных частей относительно той же оси:
, (13)
что непосредственно следует из свойств определенного интеграла. Таким образом, для вычисления момента инерции сложной фигуры надо разбить ее на ряд простых фигур, вычислить моменты инерции этих фигур, а затем просуммировать их.
Пример 3.
Определить момент инерции сечения, показанного на рис. 4.12, относительно оси симметрии, a=10 см.
Рис.4.12
Решение.
Разбиваем заданное сечение на простейшие элементы: I - Равнобедренный треугольник, II - прямоугольник, III - круг.
Момент инерции сложной фигуры относительно оси z согласно формуле (13):
.Определяем моменты инерции слагаемых простейших элементов:
Для равнобедренного треугольника:
; для прямоугольника согласно формуле:
; для круга согласно формуле:
.Окончательно получим:
Iz=4,0a4+10,67a4-0,0491a4=14,6a4=14,6×104=1,46×105 см4.
Пример 4.
Определить момент инерции симметричного сечения, показанного на рис. 4.13, относительно вертикальной оси симметрии y. Двутавр №10 (ГОСТ 8239-56). Швеллер №5 (ГОСТ 8240-56).
Рис.4.13
Решение.
Разбиваем исходное сечение на простейшие элементы, моменты инерций которых приводятся в справочниках: I - двутавр, II и III - швеллеры.
По сортаменту на стандартные прокатные профили имеем:
Для двутавра №10 (ГОСТ 8239-56): H=10 см, B=7 см, F=14,2 см2, Ix=244 см4, Iy=35,3 см4.
Для швеллера №5 (ГОСТ 8240-56): h=5 см, b=3,7 см, F=6,90 см2, Ix=26,1 см4, Iy=8,41 см4, x0=1,35 см.
Момент инерции сечения относительно оси y согласно (13)
т.к. оба швеллера расположены идентично относительно оси y.
Для двутавра
.Для швеллера
сортам.=26,1 см4.Окончательно имеем: