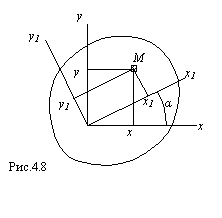
.Изменение моментов инерции сечения при повороте осей координатНайдем зависимость между моментами инерции относительно осей х, у и моментами инерции относительно осей х₁, у₁, повернутых на угол . Пусть J_x> J_y и положительный угол отсчитывается от оси х против часовой стрелки. Пусть координаты точки М до поворота – x,y, после поворота – x₁, y₁ (рис. 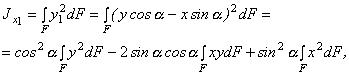4.14).Рис.4.14Из рисунка следует:Теперь определим моменты инерции относительно осей х₁ и у₁:или . (14)Аналогично: . (15) (16)Сложив почленно уравнения (14), (15), получим: ,т.е. 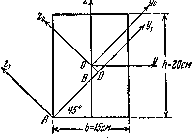сумма моментов инерции относительно любых взаимно перпендикулярных осей остается постоянной и не изменяется при повороте системы координат.Пример 5.Найти моменты инерции прямоугольника (рис.4.15) относительно осей и и центробежный момент его относительно тех же осей.Рис.4.15Решение.Центральные оси у и z как оси симметрии будут главными осями; моменты инерции сечения относительно этих осей равны:

---

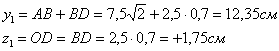
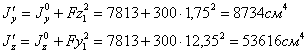
Центральные моменты относительно повернутых осей и равны:Центробежный момент инерции относительно осей и равен:Координаты центра тяжести прямоугольника относительно осей и равны:Моменты инерции относительно осей и равны:Центробежный момент инерции равен:Главные оси инерции и главные моменты инерцииС изменением угла поворота осей каждая из величин и меняется, а сумма их остается неизменной. Следовательно, существует такое значение , при котором моменты инерции достигают экстремальных значений, т.е. один из моментов инерции достигает своего максимального значения

---

, в то время другой момент инерции принимает минимальное значение. Для нахождения значения возьмем первую производную от (или ) и приравняем ее нулю:

,

или

,

откуда

. (17)

Покажем, что относительно полученных осей центробежный момент инерции равен нулю. Для этого приравняем правую часть уравнения (16) нулю:

,

откуда

,

т.е. получили ту же формулу для .

Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты инерции принимают экстремальные значения называются главными осями. Если эти оси являются также и центральными, то они называются главными центральными осями. Осевые моменты инерции относительно главных осей называются главными моментами инерции.

Обозначим главные оси через и . Тогда

,

,

.

Если сечение имеет ось симметрии, то эта ось всегда является одной из главных центральных осей инерции сечения.

В литературе главные оси иногда обозначаются через и .

Главные моменты инерции и могут быть также определены по формулам:

---

При повороте осей координат удовлетворяется следующее равенство:Моменты сопротивления относительно главных центральных осей uи vмогут быть подсчитаны по формулам:где , - координаты точек сечения, наиболее удаленных от главных центральных осей uи v. Эти координаты можно вычислить, используя связь между координатами в повернутых на угол осях по формулам:Понятие о радиусе и эллипсе инерции сеченияРадиусом инерции плоской фигуры относительно какой-либо оси, называется длина перпендикуляра, отсчитываемая от этой оси и вычисляемая по формуле: (18) После определения моментов инерции относительно главных осей можно построить эллипс инерции – это эллипс, полуоси которого равны радиусам инерции относительно главных осей. Радиус инерции

---

откладывается вдоль главной оси , а – вдоль оси (рис. 4.16). Построение эллипса инерции удобно использовать для анализа правильности определения моментов инерции. Эллипс инерции должен быть вытянут в том направлении, в котором вытянута фигура.Рис.4.16

---

Смотрите также файлы

• Сибирский.docx

• новосибирский государственный технический университет факультет бизнеса.docx

• Выберите из представленных федеральных занятий одно, фрагмент которого Вы планируете разработать.doc

• 1. Экономические потребности, блага и ресурсы. Проблема выбор а.docx

• Выполнил студент 1го курса.pptx