ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.12.2023
Просмотров: 110
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Суперпозиция волны.
План:
1. Принцип суперпозиции волн.
2. Когерентные волны. Интерференция и дифракция волн.
3. Групповая скорость. Стоячие волны.
4. Звук волны, их высота, давление и энергия.
Суперпозиция волны.
1. Принцип суперпозиции волн.
Принцип суперпозиции (наложения) волн установлен на опыте. Он состоит в том, что в линейной среде волны от разных источников распространяются независимо, и накладываясь, не изменяют друг друга. Результирующее смещение частицы среды в любой момент времени равно геометрической сумме смещений, которые частица получит, участвуя в каждом из слагаемых волновых процессов.
Согласно принципу суперпозиции накладываться друг на друга без взаимного искажения могут волны любой формы. В результате наложения волн результирующее колебание каждой частицы среды может происходить по любому сложному закону. Такое образование волн называется волновым пакетом. Скорость движения волнового пакета не совпадает со скоростью ни с одной из слагаемых волн. В этом случае говорят о скорости
волнового пакета. Скорость перемещения максимума группы волн (волнового пакета)называется групповой скоростью. Она равна скорости переноса энергии волнового пакета.На практике мы всегда имеем дело с группой волн, так как синусоидальных волн, бесконечных в пространстве и во времени, не существует. Любая ограниченная во времени и пространстве синусоидальная волна есть волновой пакет (его называют цуг волны). Групповая скорость такого пакета совпадает с фазовой скоростью бесконечных синусоидальных волн, результатом сложения которых он является.
В общем виде связь между групповой и фазовой скоростями имеет вид:
.Электромагнитные волны.
1. Электромагнитными волнами называются возмущения электромагнитного поля (т.е. переменное электромагнитное поле), распрострняющиеся в пространстве.
Утверждение о существовании электромагнитных волн является непосредственным следствием решения системы уравнений Максвелла. Согласно этой теории следует, что переменное электромагнитное поле распространяется в пространстве в виде волн, фазовая скорость которых равна:
где
- скорость света в вакууме,
,
- электрическая и магнитная постоянные,
,
- соответственно диэлектрическая и магнитная проницаемость среды.2. Электромагнитные волны - поперечные волны. Векторы Е и Н поля электромагнитной волны взаимно перпендикулярны друг другу. Вектор скорости волны
и векторы Е и Н образуют правую тройку векторов (Рисунок 2.1.4).Для сравнения ориентации тройки векторов
, Е и Н на рисунке приведено расположение осей декартовой системы координат. Такое сопоставление уместно и в дальнейшем будет использовано для определения проекций векторов Е и Н на координатные оси.Р
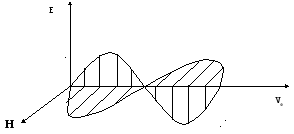исунок 2.1.4Взаимно перпендикулярные векторы Е и Н колеблются в одной фазе (их колебания синфазные). Модули этих векторов связаны соотношением:
которое справедливо для любой бегущей электромагнитной волны независимо от формы ее волновых поверхностей.
3.По форме волновых поверхностей волны могут быть плоские, эллиптические, сферические и т.д..
Монохроматической волной называется электромагнитная волна одной определенной частоты. Монохроматическая волна не ограничена в пространстве и во времени. В каждой точке электромагнитного поля монохроматической волны проекции векторов Е и Н на оси координат совершают гармонические колебания одинаковой частоты
. Например, дляплоской монохроматической волны, распространяющейся вдоль положительного направления оси ОУ, как показано на рисунке 2.1.3.,ее уравнение имеет вид:
Такие волны называются плоско (или линейно) поляризованными волнами.
Плоскость, в которой происходит колебание вектора Е называют плоскостью поляризации линейно поляризованной волны, а плоскость колебаний вектора Н – плоскостью колебаний. Ранее эти названия были обратными (см. [1]).
6. Все сказанное о стоячих волнах в упругих средах относится и к электромагнитным волнам. В этом случае, однако, волна характеризуется не одним вектором, а двумя взаимно перпендикулярными векторами Е и Н.
Стоячая электромагнитная волна состоит из двух стоячих волн - магнитной и электрической, колебания которых сдвинуты по фазе на
.7. Энергия электромагнитных волн.
Объемная плотность энергии электромагнитного поля в линейной изотропной среде задается соотношением:
с - скорость света в вакууме.
В случае плоской линейно поляризованной монохроматической волны, распространяющейся вдоль положительного направления ОY, напряженность электрического поля задается уравнением:
соответственно объемная плотность энергии этой волны
Значение объемной плотности энергии волны меняется за период от 0 до
.Среднее за период значение энергии равно:
.8. Вектор плотности потока энергии электромагнитной волны называется вектором Умова - Пойнтинга:
Для линейно поляризованной монохроматической волны вектор Пойнтинга направлен в сторону распространения волны и численно равен:
Интенсивность электромагнитной волны равна модулю среднего значения вектора Пойнтинга за период его полного колебания:
Интенсивностью электромагнитной волны называется физическая величина, численно равная энергии, переносимая волной за единицу времени через единицу площади поверхности, расположенной перпендикулярно к направлению распространения волны.
Интенсивность бегущей монохроматической волны:
- фазовая скорость волны, 
среднее значение объемной плотности энергии поля волны.Интенсивность света (электромагнитных волн, рассматриваемых в оптике) прямо пропорциональна квадрату амплитуды колебаний вектора напряженности Е поля световой волны.
2. Когерентные волны. Интерференция и дифракция волн.
Интерференция явление, характерное для всякого движения. Интерференция света наложение световых пучков, при котором они в одних местах гасят друг друга, а в других усиливают. При ИС интенсивность суммарного пучка не равна сумме интенсивностей составляющих.
Необходимым условием наблюдения ИС является когерентность пучков света. Когерентность колебаний (от лат. cohaerens находящийся в связи) наличие неизменных соотношений между фазами различных колебаний. Простейший случай когерентных колебаний два гармонических колебания с равными частотами и постоянной разностью фаз.
В случае световых волн когерентные пучки могут быть получены только от одного и того же источника света. Для получения двух когерентных пучков свет, испускаемый источником, разделяется на два пучка, которые проходят различные пути и затем сводятся вместе.
Результат ИС зависит от оптической разности хода интерферирующих пучков. Если один пучок проходит в среде с показателем преломления
геометрический путь 
, а другой - в среде с показателем преломления 
путь 
, то разность хода 
равна
,где
длина волны света, а 
порядок интерференции, величина, определяющая результат И. Если целое число, то световые волны усиливают друг друга и возникают максимумы интенсивности. При разности хода, составляющей нечетное число полуволн 
, наблюдается взаимное гашение волн и возникают минимумы интенсивности. Поскольку разность хода зависит от направления пучков, то в результате получаются светлые и темные полосы, каждая из которых соединяет точки с одинаковой разностью хода.Дифракцией называется любое отклонение распространения волн вблизи препятствий от законов геометрической оптики. Явления д. можно наблюдать, если на пути распространения электромагнитной волны находятся препятствия – непрозрачные тела произвольной формы или, если свет проходит через отверстия в непрозрачных экранах. Благодаря д. волны могут попадать в область геометрической тени. Если бы законы геометрической оптики выполнялись строго, то за экранами находились бы области тени, резко отграниченные от областей, куда свет попадает. Д. приводит к тому, что вместо резкой границы между светом и тенью получается сложная картина распределения интенсивности света. Д. явления тем сильнее выражены, чем меньше размеры экранов и отверстий в них или чем больше длина волны.