Файл: Федеральное агентство по образованию иркутский государственный технический университет.doc

Расчетная площадь стойки при двустороннем ребре

A_s= (2b_r+ t_w)t_r+ 2ct_w = (2 · 9 + 1,2) 0,7 + 2 ∙ 22,85 ∙ 1,2) = 68,28 см².

Момент инерции сечения стойки

I_z = t_r³/12 + 2ct_w³/12 = 0,7 (2 ∙ 9 +1,2)³ / 12 + 2 ∙ 22,85 ∙ 1,2³ / 12 = 412,88 см⁴.

Радиус инерции

i_z = = = 2,46 см.

Гибкость стойки

λ_z = l_ef /i_z = 150 / 2,46 = 60,98.

Условная гибкость



Производим проверку устойчивости стойки:



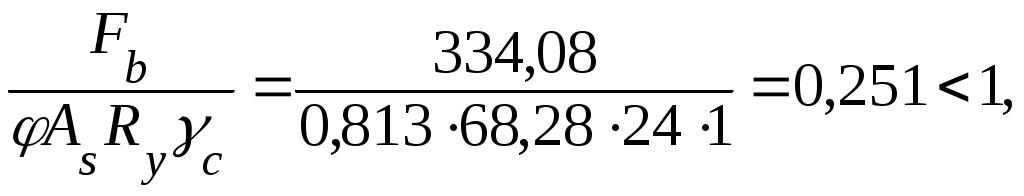
где φ = 0,813 – коэффициент устойчивости при центральном сжатии, принимаемый по табл. 3.11 в зависимости от условной гибкости λ_z для типа кривой устойчивости ^״b^״; тип кривой устойчивости зависит от формы сечений и толщины проката (табл. 3.12), при условной гибкости λ_z ≤ 0,4 коэффициент φ принимается равным единице.

Условие выполняется.

Таблица 3.11

Коэффициенты устойчивости при центральном сжатии

Условная гибкость	Коэффициент  для типов кривых устойчивости			Условная гибкость	Коэффициент  для типов кривых устойчивости
	a	b	c		a	b	c
0,4	999	998	992	3,2	660	602	526
0,6	994	986	950	3,4	615	562	492
0,8	981	967	929	3,6	572	524	460
1,0	968	948	901	3,8	530	487	430
1,2	954	927	878	4,0	475	453	401
1,4	938	905	842	4,2	431	421	375
1,6	920	881	811	4,4	393	392	351
1,8	900	855	778	4,6	359	359	328
2,0	877	826	744	4,8	330	330	308
2,2	851	794	709	5,0	304	304	289
2,4	820	760	672	5,2	281	281	271
2,6	785	722	635	5,4	261	261	255
2,8	747	683	598	5,6	242	242	240
3,0	704	643	562	5,8	226	226	226

---

П р и м е ч а н и е. Значения коэффициента  в таблице увеличены в 1000 раз.

Устойчивость стенок балок не требуется проверять, если условная гибкость стенки _w не превышает значений:

3,5 – для балок с двухсторонними поясными швами при отсутствии местной нагрузки на пояс балки;

3,2 – для таких же балок с односторонними поясными швами;

2,5 – для балок с двухсторонними поясными швами при наличии местной нагрузки на пояс.

Таблица 3.12

---

Характеристики кривых устойчивости

Тип сечения			Тип кривой устойчивости	Значение коэффициентов
				α	β	λmax
			a	0,03	0,06	3,8
			b	0,04	0,09	4,4
			c	0,04	0,14	5,8

В нашем примере следовательно, требуется проверка стенки на местную устойчивость.

Расчет на устойчивость стенки балки симметричного сечения, укрепленной только поперечными основными ребрами жесткости, при отсутствии местных напряжений смятия и условной гибкости стенки выполняется по формуле



при наличии местного напряжения (см. рис. 3.11) – по формуле



где σ,и σ_loc – действующие нормальные, касательные и локальные напряжения в месте соединения стенки с поясом от средних значений M,Q и F_b в пределах отсека; если длина отсека больше его расчетной высоты (a

---

> h_w), то M и Q определяются для наиболее напряженного участка отсека с длиной, равной высоте отсека h_w; если в пределах отсека MиQменяют знак, то их средние значения следует вычислять на участке отсека с одним знаком;

σ_сr , σ_loc,сr, τ_сr – критические напряжения, определяемые по СНиП [6].

Проверку местной устойчивости стенки производят в наиболее нагруженных отсеках: первом от опоры; среднем и, при наличии изменения сечения балки по длине, в отсеке с измененным сечением.

Проверка местной устойчивости стенки в среднем отсеке балки (рис. 3.16).



Рис. 3.16. Распределение изгибающих моментов и поперечных сил

в среднем отсеке
Так как а = 3 м > h_w = 1,5 м, определяем M_ср и Q_ср по середине условного отсека шириной, равной половине высоты стенки h_w, для чего вычисляем величины моментов и поперечных сил на границах расчетного участка (х₁ = 7,5 м; х₂ = 9 м):

M₁ = qx₁(l – x₁)/2 = 115,03 · 7,5 (18 – 7,5) / 2 = 4529,31 кН∙м;

M₂ = M_max = 4658,72 кН∙м;

Q₂ = 0;

M_ср = (M₁ + M₂)/2 = (4529,31 + 4658,72) / 2 = 4594,02 кН·м;

Q_ср = (Q₁ + Q₂)/2 = 172,55 / 2 = 86,28 кН.

Краевое напряжение сжатия в стенке

σ = M_ср(h_w/h)/W_x = 4594,02 (150 / 155) /21234 = 20,09 кН/см².

Среднее касательное напряжение в отсеке

τ = Q_ср/(h_wt_w) = 86,28 / (150 ∙ 1,2) = 0,48 кН/см².

Локальное напряжение σ_loc= 0.

Критическое нормальное напряжение



где c_сr = 33,4 – коэффициент, определяемый по табл. 3.13 в зависимости от значения коэффициента δ, учитывающего степень упругого защемления стенки в поясах,

---

здесь β = ∞ – при непрерывном опирании плит;

β = 0,8 – в прочих случаях.

Таблица 3.13

Значения коэффициента с_сr в зависимости от значения δ

	 0,8	1,0	2,0	4,0	6,0	10,0	30
ссr	30,0	31,5	33,3	34,6	34,8	35,1	35,5

Критическое касательное напряжение определяется по формуле



где – отношение большей стороны отсека a или h_w к меньшей d;



здесь d = h_w = 1,5 м < a = 3 м.

Проверяем местную устойчивость стенки:



Устойчивость стенки в середине балки обеспечена.

Проверка местной устойчивости стенки в месте изменения сечения балки на расстоянии х = 3 м от опоры.

Расчетные усилия равны:

М₁ = 2588,18 кН·м; Q₁ = 690,18 кН.

Краевое напряжение сжатия в стенке

σ = M₁(h_w/h)/W₁ = 258818 (150 / 155) /13357 = 18,75 кН/см².

Среднее касательное напряжение в отсеке

τ = Q₁/(h_wt_w) = 690,18 / (150 ∙ 1,2) = 3,83 кН/см².

Локальное напряжение σ_loc= 0.

Критическое нормальное напряжение



где c_сr = 31,8 – по табл. 3.13 в зависимости от



Критическое касательное напряжение

---