Файл: Федеральное агентство по образованию иркутский государственный технический университет.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.12.2023
Просмотров: 847
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
торцевой поверхности (при наличии пригонки)
Расчетные сопротивления срезу и растяжению болтов
Основные размеры элементов подкрановых балок
Расчетные сопротивления растяжению фундаментных болтовRba
Рис. 9.1 К определению расчетных усилий в разрезной подкрановой балке:
г – схема загружения балки одним краном для определения прогиба
(см. проверку местной устойчивости стенки в среднем отсеке).
Производим проверку:
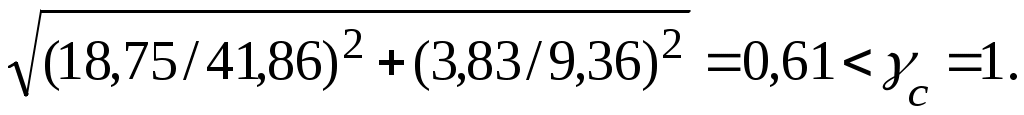
Стенка в отсеке балки с измененным сечением устойчива.
Проверка местной устойчивости стенки в первом отсеке в сечении на расстоянии от опоры x1 = a1/2 = 1,5 / 2 = 0,75 м (рис. 3.17),
где a1= hw= 1,5 м.

Рис. 3.17. К проверке местной устойчивости стенки балки у опоры
Определяем усилия:
M1 = qx1(l – x1)/2 = 115,03 · 0,75 (18 – 0,75) / 2 = 744,1 кН∙м;
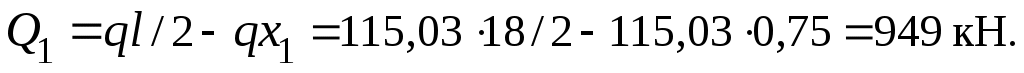
Краевое напряжение сжатия в стенке
σ = M1(hw/h)/W1 = 74410 (150 / 155) /13357 = 5,39 кН/см2.
Среднее касательное напряжение в отсеке
τ = Q1/(hwtw) = 949 / (150 ∙ 1,2) = 5,27 кН/см2.
Локальное напряжение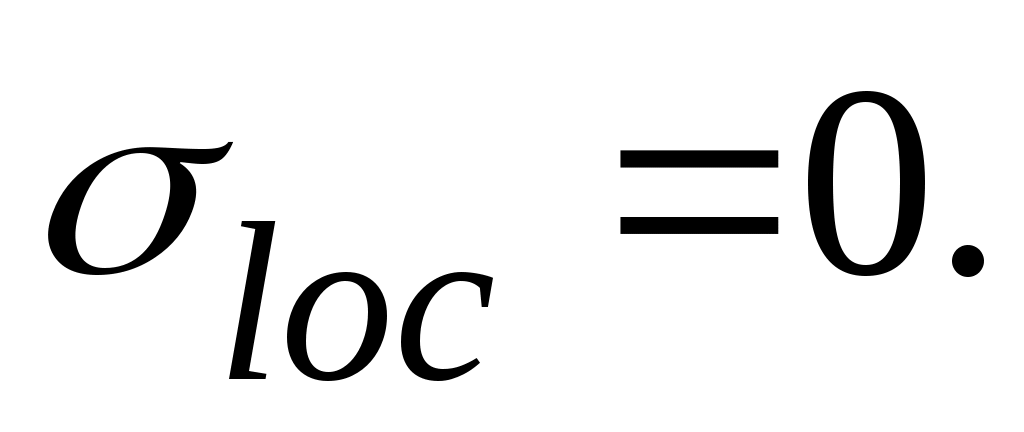
Критическое нормальное напряжение
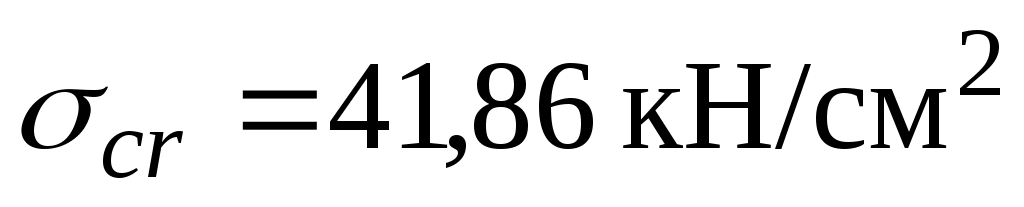 при = 1,16.
при = 1,16.
Критическое касательное напряжение определяется по формуле

где ;
;

здесь d = hw = a1 = 1,5 м – меньшая из сторон отсека.
Производим проверку:
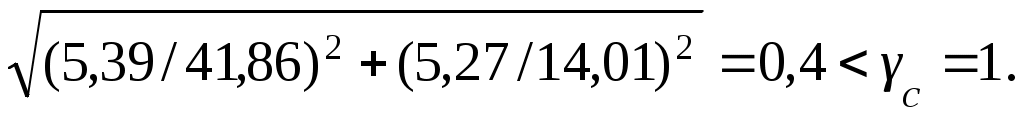
Стенка в первом от опоры отсеке устойчива.
В случае невыполнения условий устойчивости стенки необходимо увеличить толщину стенки tw или уменьшить расстояние между поперечными ребрами жесткости а, затем повторно произвести проверку ее устойчивости.
Проверка местной устойчивости стенки балки при наличии местных напряжений (σloc 0).
При наличии местных напряжений проверку стенки на местную устойчивость следует выполнять в зависимости от значения a/hw, при этом значения M иQ определяют в одном сечении балки.
Значения критических напряжений определяются в предположении выпучивания стенки между ребрами жесткости при ее потере устойчивости по одной полуволне при частом расположении ребер (a/hw 0,8) и при более редкой расстановке ребер жесткости (a/hw > 0,8) – по одной или двум полуволнам.
Значение критического нормального напряжения σcr при a/hw 0,8 определяется так же, как и при отсутствии местных напряжений по формуле
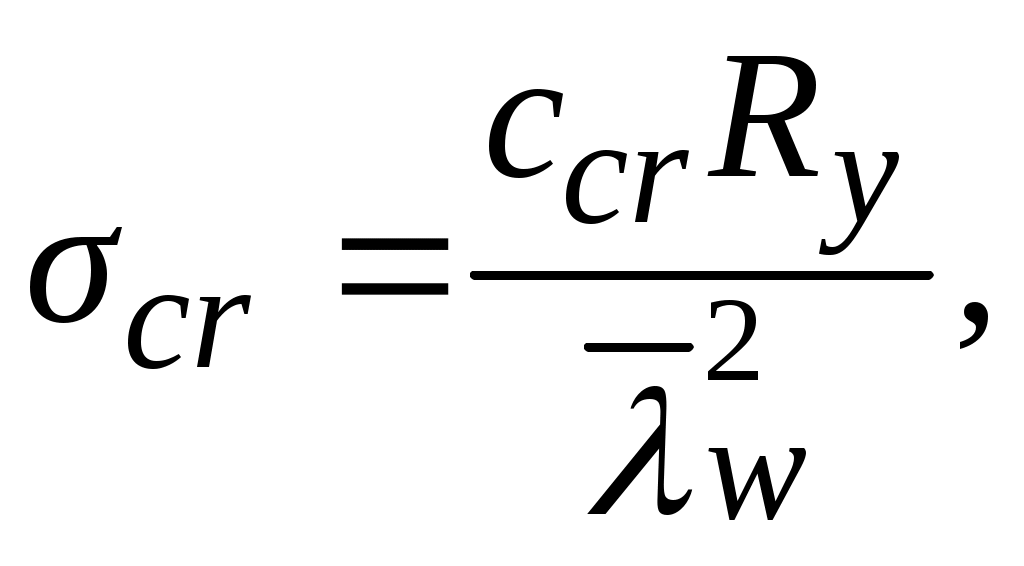
где ccr находится по табл. 3.13;
Критическое напряжение потери устойчивости от действия местных напряжений определяется по формуле
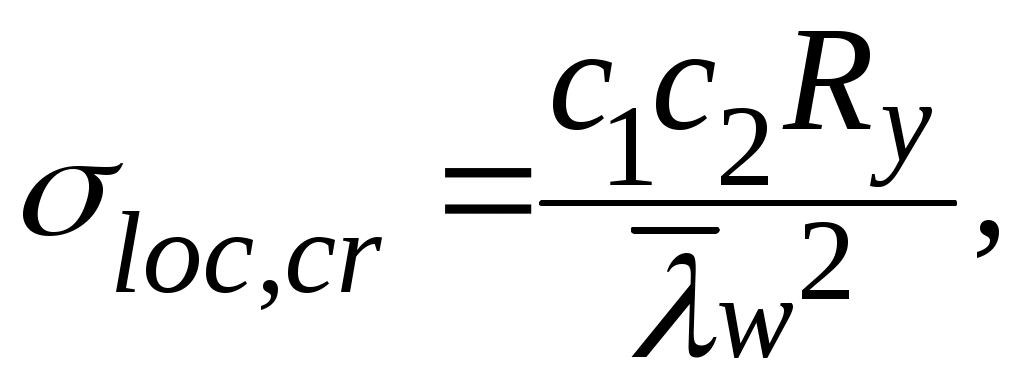
где с1 – коэффициент, принимаемый по табл. 3.14 в зависимости от a/hw – соотношения сторон проверяемой пластины и значения, ρ = 1,04lef /hw – относительной длины загружения пластины местной нагрузкой lef к высоте стенки hw (см. рис. 3.11), здесь lef = b + 2tf ;
с2 – коэффициент, принимаемый по табл. 3.15 в зависимости от отношенияa/hw и значения δ.
Таблица 3.14
Значения коэффициента c1
Таблица 3.15
Значения коэффициента c2
При отношении a/hw> 0,8 рассматривают два случая проверки устойчивости стенки:
В первом случае вычисляются критическое нормальное σcr и локальное σloc,cr напряжения по следующим формулам:
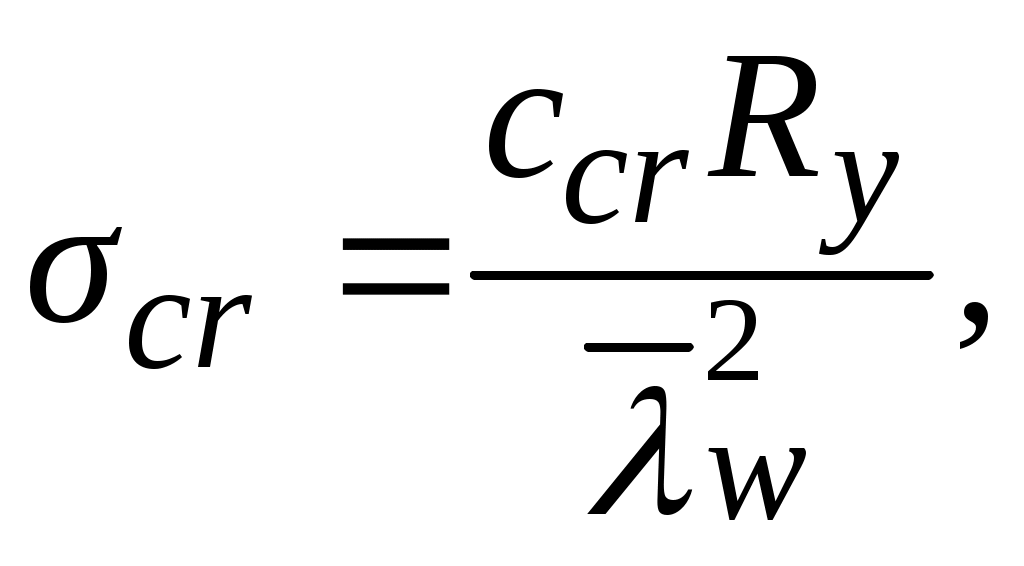
где ccr определяется по табл. 3.13;

где для его вычисления при определении коэффициентов c1 и c2 по табл. 3.14 и 3.15 вместо a необходимо принять a1 = 0,5aпри0,8 ≤ a/hw ≤ 1,33 и a1 = 0,67hwпри a/hw > 1,33.
Во втором случае их определяют так:
– критическое нормальное напряжение

где ccr определяется по табл. 3.16;
– критическое локальное напряжение потери устойчивости

где коэффициенты c1 и c2 определяют по фактическому отношению сторонa/hw(если a/hw> 2, в расчете принимаютa/hw= 2).
Таблица 3.16
Значения коэффициента ccr в зависимости
от отношения a/hw
Значение критического касательного напряжения τcr во всех случаях вычисляют по фактическим размерам отсека.
Проверка местной устойчивости стенки при наличии местных напряжений в среднем отсеке (в качестве примера).
При принятом шаге поперечных ребер жесткости а = 3 м отношение
Первая проверка. Локальное напряжение от сосредоточенной нагрузки loc= 13,58 кН/см2.
Нормальное напряжение в среднем отсеке = 20,9 кН/см2.
Среднее касательное напряжение τ = 0,48 кН/см2.
Значение критического нормального напряжения
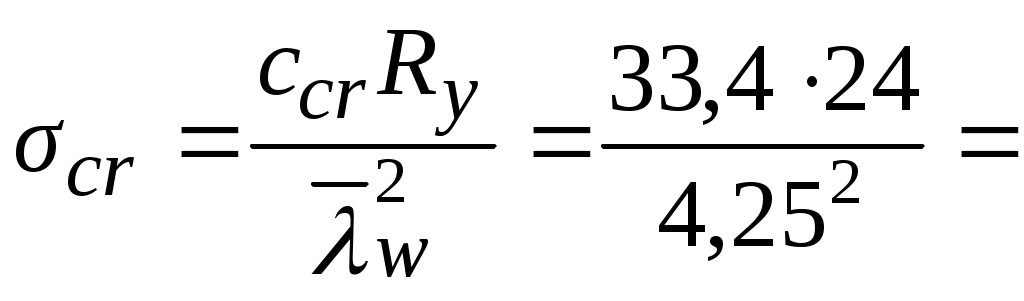 44,38 кН/см2,
44,38 кН/см2,
где ccr= 33,4, определенное по табл. 3.13 при δ = 2,16.
Значение критического локального напряжения

где при вычислении коэффициентов с1 и с2 при a/hw = 2 > 1,33 вместо а принимаем а1 = 0,67hw= 0,67 · 150 = 100,5 см, следовательно,
a1/hw = 100,5 / 150 = 0,67;
ρ = 1,04lef /hw = 1,04 ∙ 20,5 / 150 = 0,14 (здесь lef = b + 2tf = 15,5 + 2∙2,5 = = 20,5 см – условная длина распределения сосредоточенной нагрузки);
с1 = 30,68 – коэффициент, определяемый по табл. 3.14 в зависимости отa1/hw = 0,67 и ρ = 0,14;
с2 = 1,64 – коэффициент, определяемый по табл. 3.15 в зависимости отa1/hw = 0,67 и δ = 2,16.
Значение критического касательного напряжения
Производим проверку:
Стенка в отсеке балки с измененным сечением устойчива.
Проверка местной устойчивости стенки в первом отсеке в сечении на расстоянии от опоры x1 = a1/2 = 1,5 / 2 = 0,75 м (рис. 3.17),
где a1= hw= 1,5 м.

Рис. 3.17. К проверке местной устойчивости стенки балки у опоры
Определяем усилия:
M1 = qx1(l – x1)/2 = 115,03 · 0,75 (18 – 0,75) / 2 = 744,1 кН∙м;
Краевое напряжение сжатия в стенке
σ = M1(hw/h)/W1 = 74410 (150 / 155) /13357 = 5,39 кН/см2.
Среднее касательное напряжение в отсеке
τ = Q1/(hwtw) = 949 / (150 ∙ 1,2) = 5,27 кН/см2.
Локальное напряжение
Критическое нормальное напряжение
Критическое касательное напряжение определяется по формуле

где
здесь d = hw = a1 = 1,5 м – меньшая из сторон отсека.
Производим проверку:
Стенка в первом от опоры отсеке устойчива.
В случае невыполнения условий устойчивости стенки необходимо увеличить толщину стенки tw или уменьшить расстояние между поперечными ребрами жесткости а, затем повторно произвести проверку ее устойчивости.
Проверка местной устойчивости стенки балки при наличии местных напряжений (σloc 0).
При наличии местных напряжений проверку стенки на местную устойчивость следует выполнять в зависимости от значения a/hw, при этом значения M иQ определяют в одном сечении балки.
Значения критических напряжений определяются в предположении выпучивания стенки между ребрами жесткости при ее потере устойчивости по одной полуволне при частом расположении ребер (a/hw 0,8) и при более редкой расстановке ребер жесткости (a/hw > 0,8) – по одной или двум полуволнам.
Значение критического нормального напряжения σcr при a/hw 0,8 определяется так же, как и при отсутствии местных напряжений по формуле
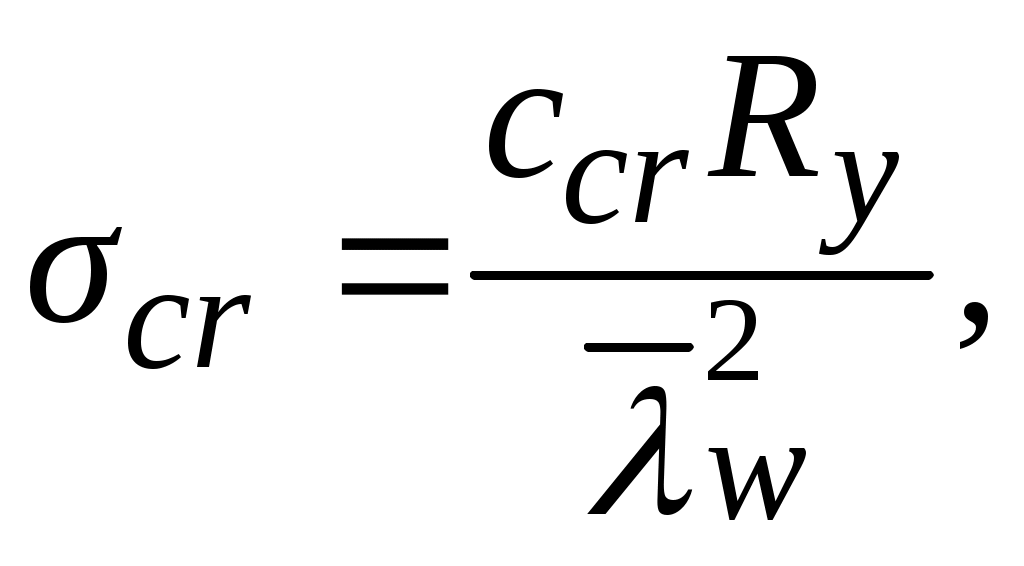
где ccr находится по табл. 3.13;
Критическое напряжение потери устойчивости от действия местных напряжений определяется по формуле
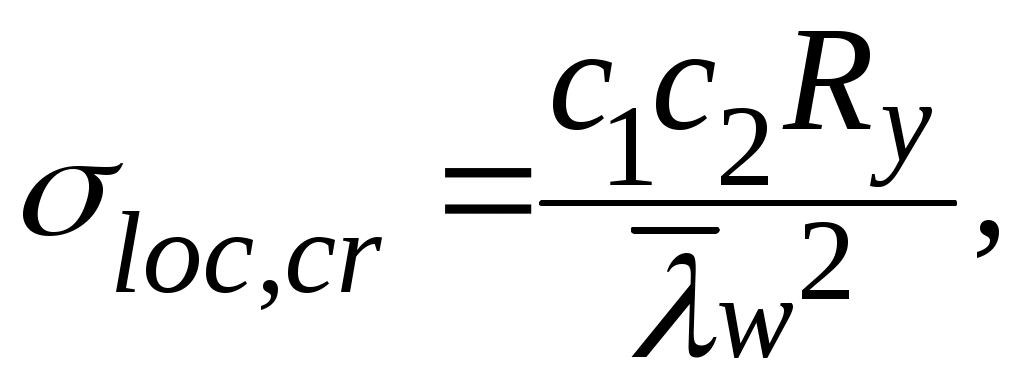
где с1 – коэффициент, принимаемый по табл. 3.14 в зависимости от a/hw – соотношения сторон проверяемой пластины и значения, ρ = 1,04lef /hw – относительной длины загружения пластины местной нагрузкой lef к высоте стенки hw (см. рис. 3.11), здесь lef = b + 2tf ;
с2 – коэффициент, принимаемый по табл. 3.15 в зависимости от отношенияa/hw и значения δ.
Таблица 3.14
Значения коэффициента c1
| ρ | При a/hef или a1/hef, равном | |||||||||
| ≤0,50 | 0,60 | 0,67 | 0,80 | 1,0 | 1,2 | 1,4 | 1,6 | 1,8 | ≥2,0 | |
| 0,10 | 56,7 | 46,6 | 41,8 | 34,9 | 28,5 | 24,5 | 21,7 | 19,5 | 17,7 | 16,2 |
| 0,15 | 38,9 | 31,3 | 27,9 | 23,0 | 18,6 | 16,2 | 14,6 | 13,6 | 12,7 | 12,0 |
| 0,20 | 33,9 | 26,7 | 23,5 | 19,2 | 15,4 | 13,3 | 12,1 | 11,3 | 10,7 | 10,2 |
| 0,25 | 30,6 | 24,9 | 20,3 | 16,2 | 12,9 | 11,1 | 10,0 | 9,4 | 9,0 | 8,7 |
| 0,30 | 28,9 | 21,6 | 18,5 | 14,5 | 11,3 | 9,6 | 8,7 | 8,1 | 7,8 | 7,6 |
| 0,35 | 28,0 | 20,6 | 18,1 | 13,4 | 10,2 | 8,6 | 7,7 | 7,2 | 6,9 | 6,7 |
| 0,40 | 27,4 | 20,0 | 16,8 | 12,7 | 9,5 | 7,9 | 7,0 | 6,6 | 6,3 | 6,1 |
Таблица 3.15
Значения коэффициента c2
| | При a/hef или a1/hef, равном | |||||||
| 0,50 | 0,60 | 0,67 | 0,80 | 1,00 | 1,20 | 1,40 | ≥1,60 | |
| ≤1 | 1,56 | 1,56 | 1,56 | 1,56 | 1,56 | 1,56 | 1,56 | 1,56 |
| 2 | 1,64 | 1,64 | 1,64 | 1,67 | 1,76 | 1,82 | 1,84 | 1,85 |
| 4 | 1,66 | 1,67 | 1,69 | 1,75 | 1,87 | 2,01 | 2,09 | 2,12 |
| 6 | 1,67 | 1,68 | 1,70 | 1,77 | 1,92 | 2,08 | 2,19 | 2,26 |
| 10 | 1,68 | 1,69 | 1,71 | 1,78 | 1,96 | 2,14 | 2,28 | 2,38 |
| ≥30 | 1,68 | 1,70 | 1,72 | 1,80 | 1,99 | 2,20 | 2,38 | 2,52 |
При отношении a/hw> 0,8 рассматривают два случая проверки устойчивости стенки:
В первом случае вычисляются критическое нормальное σcr и локальное σloc,cr напряжения по следующим формулам:
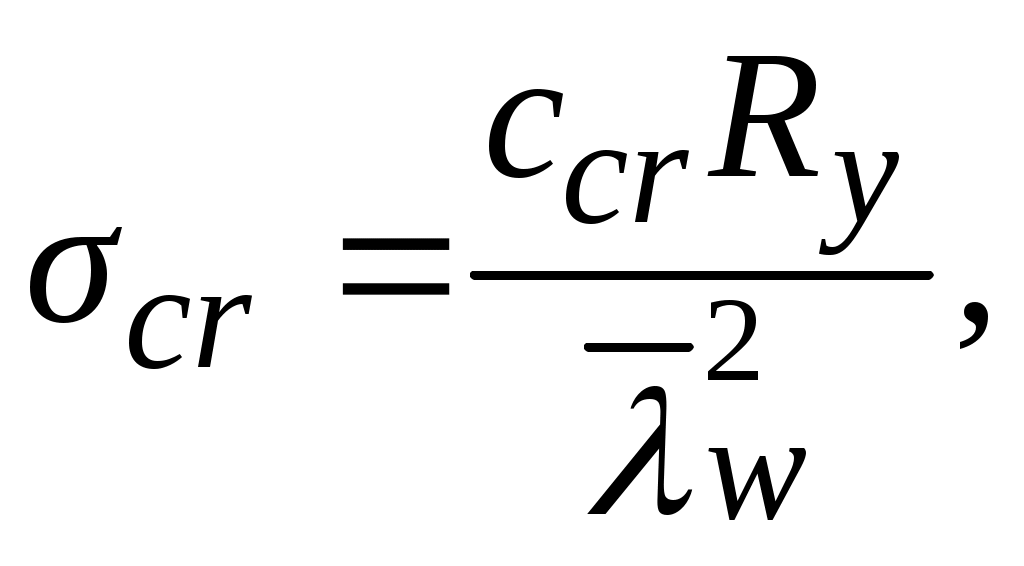
где ccr определяется по табл. 3.13;

где для его вычисления при определении коэффициентов c1 и c2 по табл. 3.14 и 3.15 вместо a необходимо принять a1 = 0,5aпри0,8 ≤ a/hw ≤ 1,33 и a1 = 0,67hwпри a/hw > 1,33.
Во втором случае их определяют так:
– критическое нормальное напряжение

где ccr определяется по табл. 3.16;
– критическое локальное напряжение потери устойчивости

где коэффициенты c1 и c2 определяют по фактическому отношению сторонa/hw(если a/hw> 2, в расчете принимаютa/hw= 2).
Таблица 3.16
Значения коэффициента ccr в зависимости
от отношения a/hw
| a/hw | ≤ 0,8 | 0,9 | 1,0 | 1,2 | 1,4 | 1,6 | 1,8 | ≥2,0 |
| cсr | По табл. 3.13 | 37,0 | 39,2 | 45,2 | 52,8 | 62,0 | 72,6 | 84,7 |
Значение критического касательного напряжения τcr во всех случаях вычисляют по фактическим размерам отсека.
Проверка местной устойчивости стенки при наличии местных напряжений в среднем отсеке (в качестве примера).
При принятом шаге поперечных ребер жесткости а = 3 м отношение
Первая проверка. Локальное напряжение от сосредоточенной нагрузки loc= 13,58 кН/см2.
Нормальное напряжение в среднем отсеке = 20,9 кН/см2.
Среднее касательное напряжение τ = 0,48 кН/см2.
Значение критического нормального напряжения
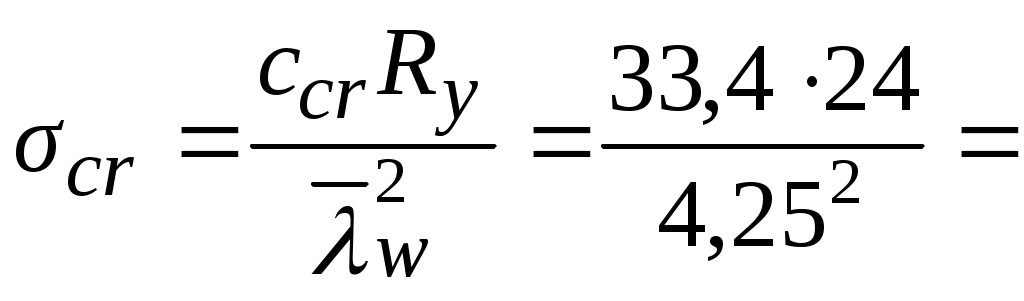 44,38 кН/см2,
44,38 кН/см2,где ccr= 33,4, определенное по табл. 3.13 при δ = 2,16.
Значение критического локального напряжения

где при вычислении коэффициентов с1 и с2 при a/hw = 2 > 1,33 вместо а принимаем а1 = 0,67hw= 0,67 · 150 = 100,5 см, следовательно,
a1/hw = 100,5 / 150 = 0,67;
ρ = 1,04lef /hw = 1,04 ∙ 20,5 / 150 = 0,14 (здесь lef = b + 2tf = 15,5 + 2∙2,5 = = 20,5 см – условная длина распределения сосредоточенной нагрузки);
с1 = 30,68 – коэффициент, определяемый по табл. 3.14 в зависимости отa1/hw = 0,67 и ρ = 0,14;
с2 = 1,64 – коэффициент, определяемый по табл. 3.15 в зависимости отa1/hw = 0,67 и δ = 2,16.
Значение критического касательного напряжения