Файл: Методические рекомендации по выполнению контрольной работы по дисциплине Высшая математика.doc
Добавлен: 09.12.2023
Просмотров: 160
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Тема 2.Операции над событиями.
Правила сложения и умножения вероятностей
События называются несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.
Два события называются совместными, если появление одного из них не исключает появление другого события в том же испытании.
Событие В называется независимым от события А, если появление события А не изменяет вероятности события В, т.е.
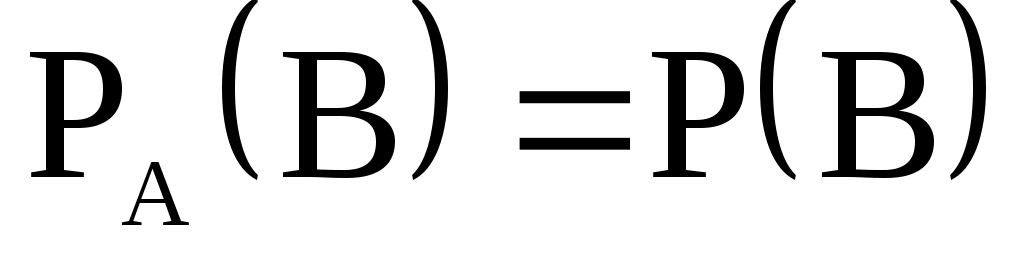 , где
, где
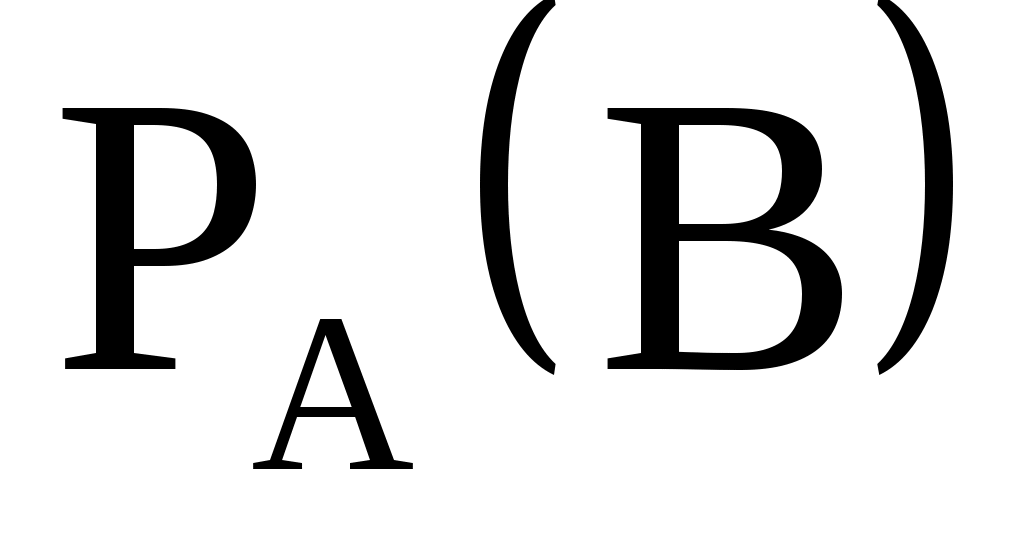 - условная вероятность наступления события В, если событие А уже наступило.
- условная вероятность наступления события В, если событие А уже наступило.
1. Сложение вероятностей.
Правило сложения вероятностей совместных событий
Для любых событий А и В
Р(А+В)=Р(А)+Р(В)-Р(АВ), где
Р(А+В) – вероятность появления хотя бы одного из двух событий,
Р(АВ) – вероятность совместного появления двух событий.
Правило сложения вероятностей несовместных событий
Р(А+В)=Р(А)+Р(В).
2. Умножение вероятностей
Правило умножения вероятностей зависимых событий
Для любых событий А и В
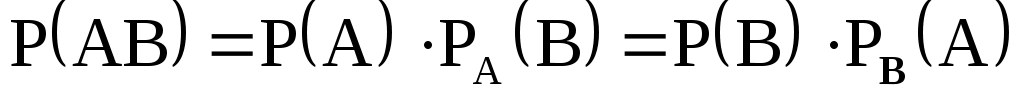 , где
, где
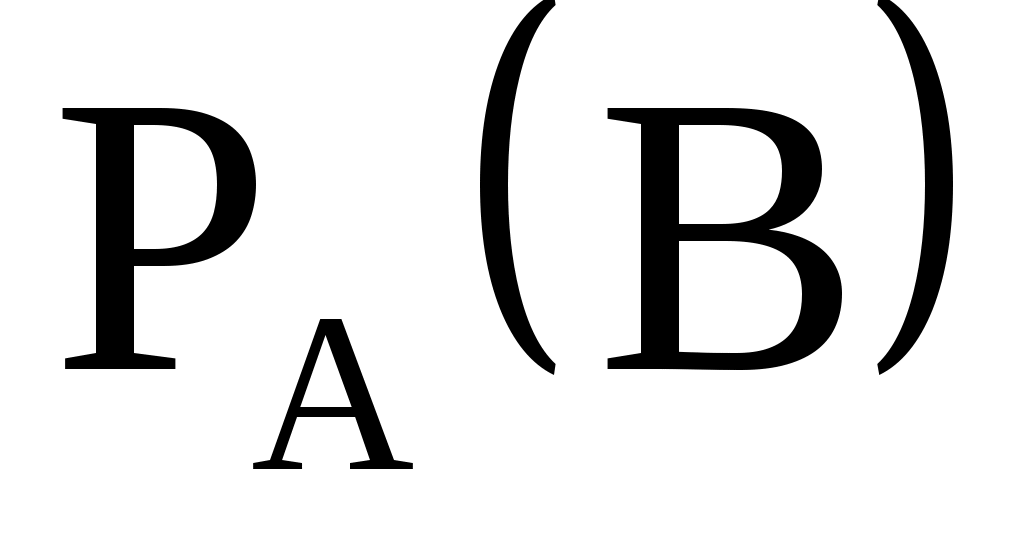 - условная вероятность наступления события В, если событие А уже наступило,
- условная вероятность наступления события В, если событие А уже наступило,
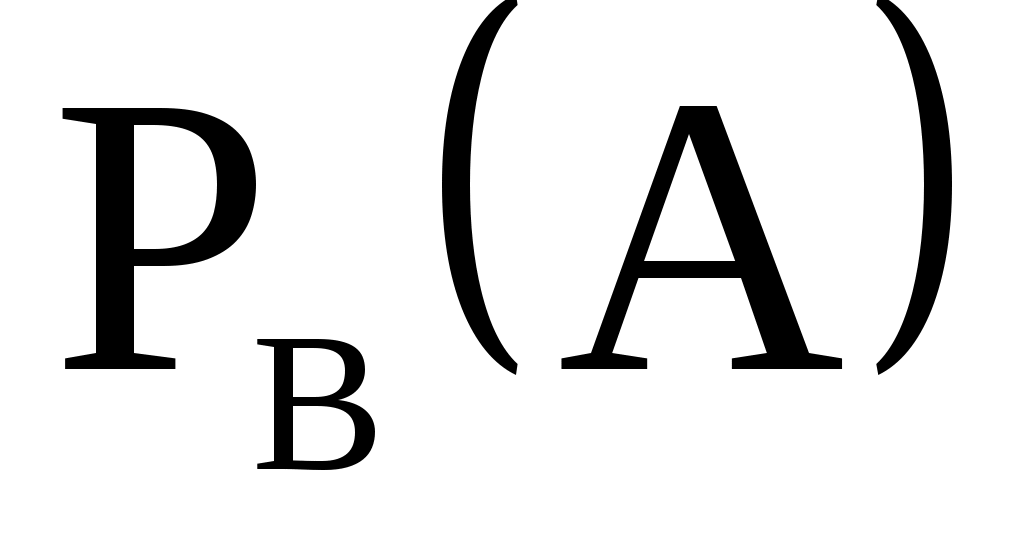 - условная вероятность наступления события А, если событие В уже наступило.
- условная вероятность наступления события А, если событие В уже наступило.
Правило умножения вероятностей независимых событий
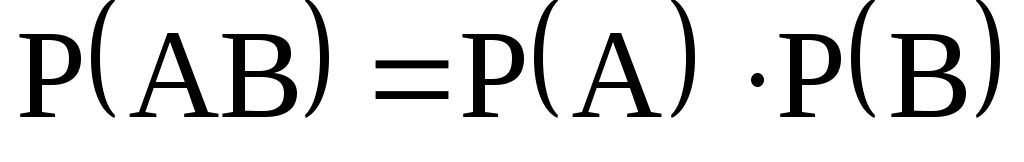 .
.
Пример 4. (Все варианты)
Экзаменационный билет содержит 3 вопроса. Вероятность того, что студент ответит на первый вопрос, рана 0,9; на второй – 0,7; на третий – 0,8. Найти вероятность того, что студент ответит:
а) только на один вопрос (варианты 1,2,3,7,10)
б) на все вопросы (варианты 7,8)
в) хотя бы на один вопрос (варианты 3,4,6)
г) по крайней мере на два вопроса (варианты 3,9)
д) на два вопроса (варианты 4,5)
Решение:
Пусть событие
= {студент ответил на первый вопрос},
 = {студент не ответил на первый вопрос},
= {студент не ответил на первый вопрос},
 ={ студент ответил на второй вопрос },
={ студент ответил на второй вопрос },
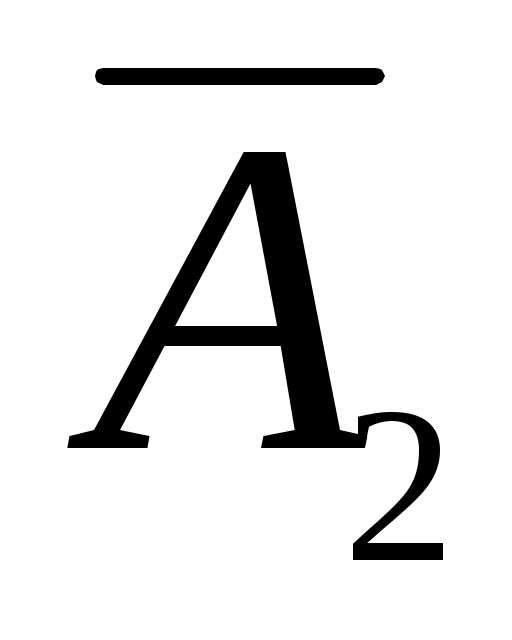 ={ студент не ответил на второй вопрос },
={ студент не ответил на второй вопрос },
 ={ студент ответил на третий вопрос },
={ студент ответил на третий вопрос },
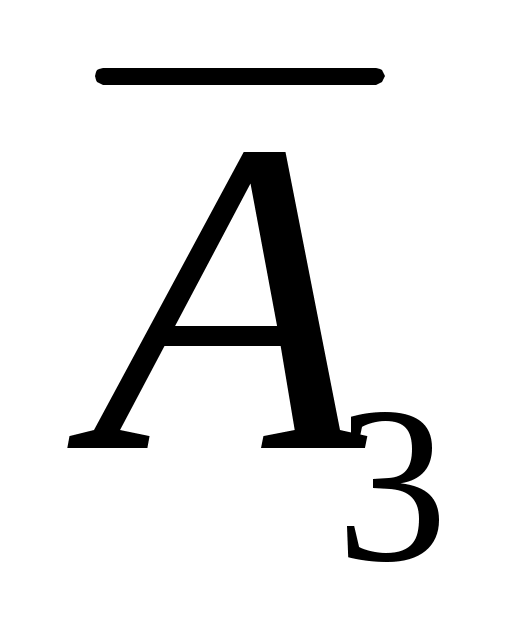 ={ студент не ответил на третий вопрос }.
={ студент не ответил на третий вопрос }.
События и
и  – противоположные, поэтому
– противоположные, поэтому 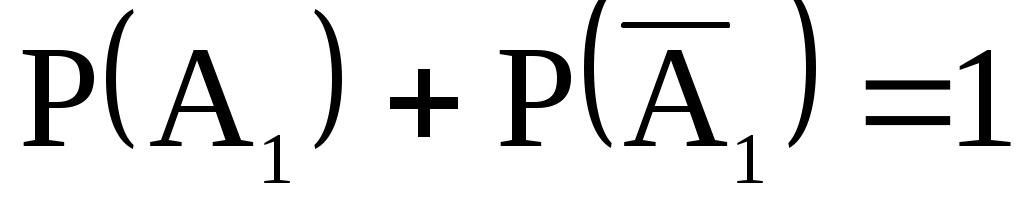 ,
, 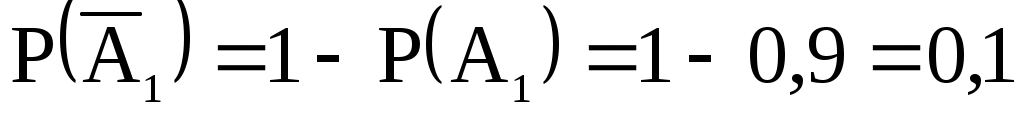 . Аналогично
. Аналогично 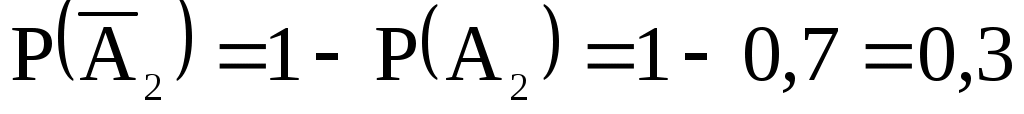 и
и
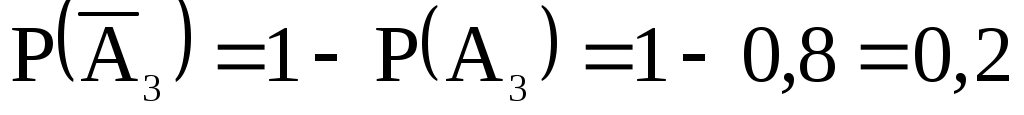 .
.
а) Событие ={студент ответил только на один вопрос}.
={студент ответил только на один вопрос}.
Появление события А означает, что наступило одно из трёх несовместных событий: либо
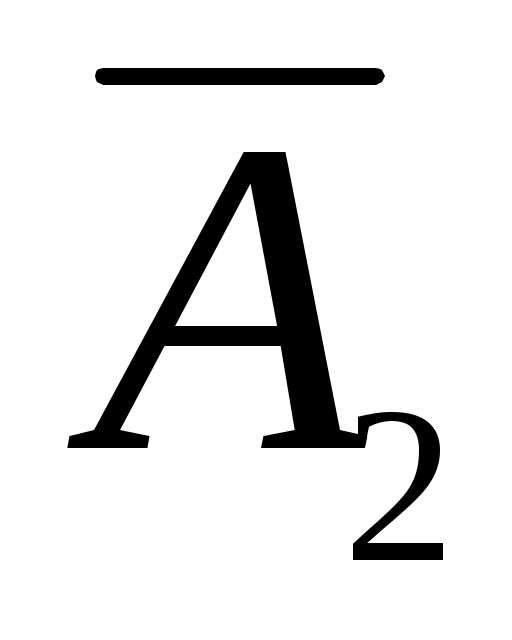
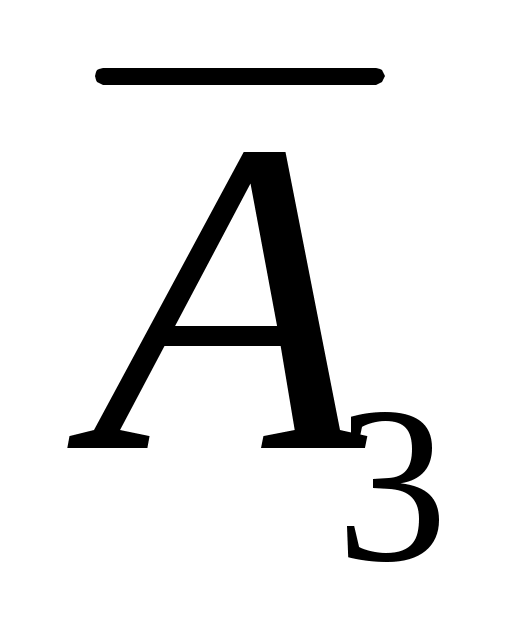 , либо
, либо 

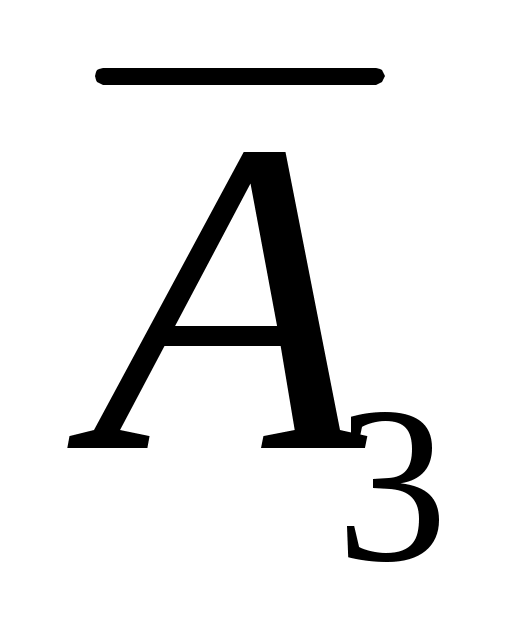 , либо
, либо 
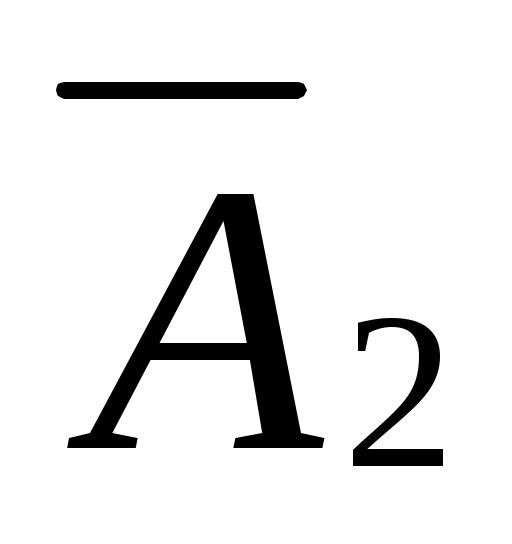
 . По правилу сложения вероятностей
. По правилу сложения вероятностей
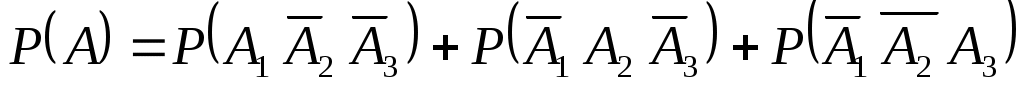
. События ,
,  ,
,  - независимые, следовательно, независимы и события
- независимые, следовательно, независимы и события  ,
,  ,
,  . По правилу умножения вероятностей для независимых событий
. По правилу умножения вероятностей для независимых событий
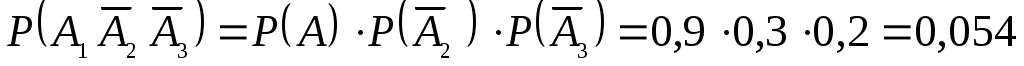 .
.
Аналогично
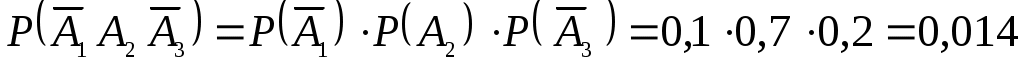 ,
,
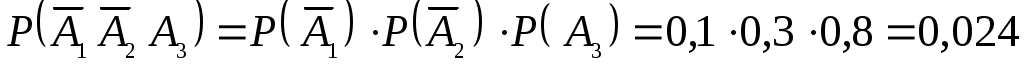 .
.
Тогда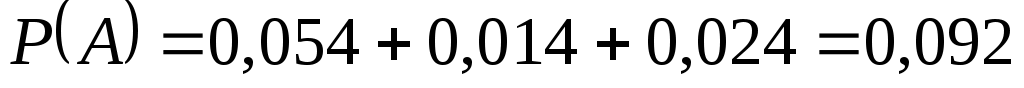 .
.
б) Событие Б={студент ответил на все вопросы}. Наступление события Б означает, что одновременно появились независимые события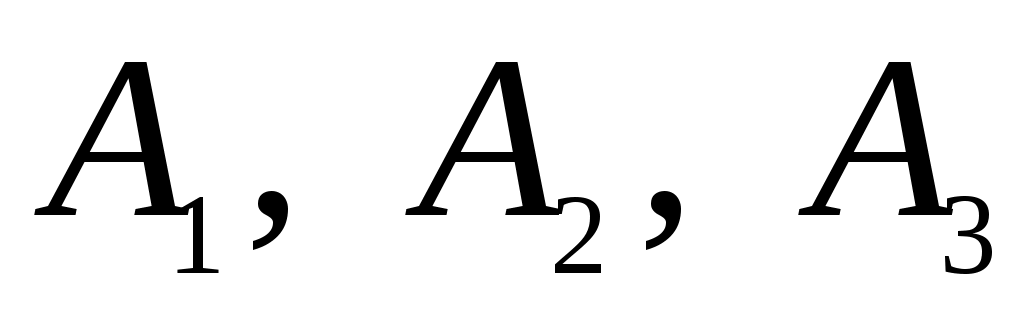 , т. е.
, т. е. 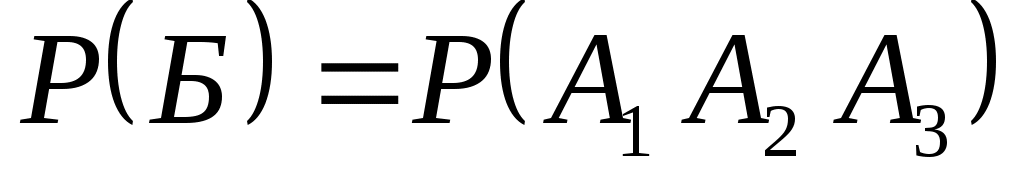 . По правилу умножения вероятностей для независимых событий
. По правилу умножения вероятностей для независимых событий
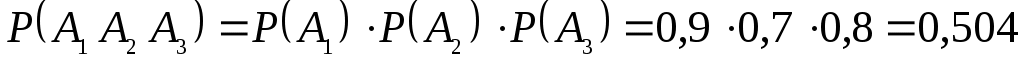 ;
; 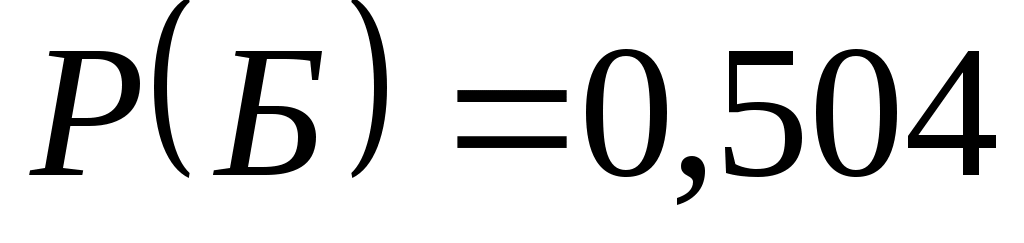 .
.
в) Событие В ={ студент ответил хотя бы на один вопрос }. Это означает, что был дан ответ на любой один вопрос, или на любые два вопроса, или на все три вопроса. Событие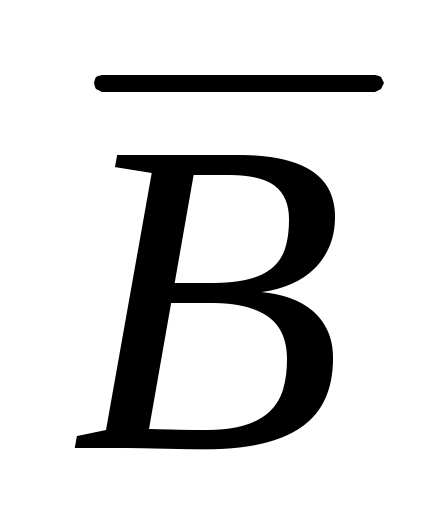 = {студент не ответил ни на один вопрос}. События B и
= {студент не ответил ни на один вопрос}. События B и 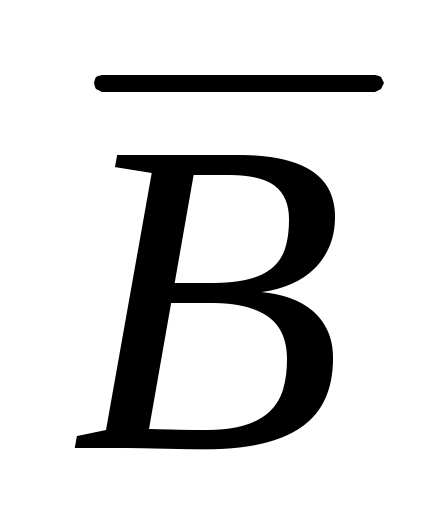 противоположны, поэтому
противоположны, поэтому 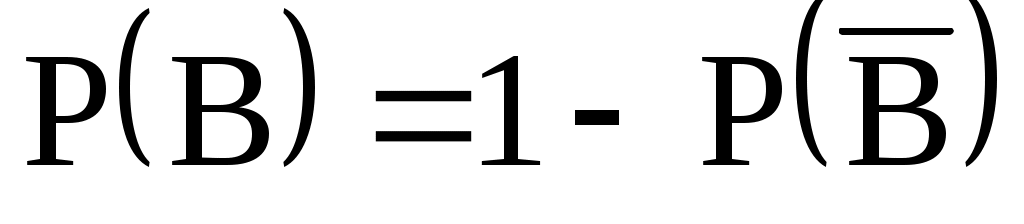 . Событие
. Событие 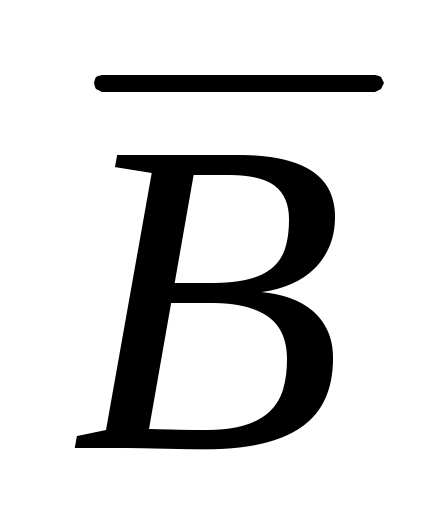 означает, что одновременно появились независимые события
означает, что одновременно появились независимые события  ,
, и
и 
, т. е.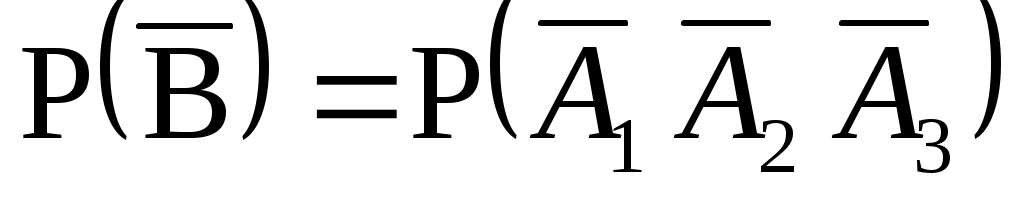 . По правилу умножения вероятностей для независимых событий
. По правилу умножения вероятностей для независимых событий 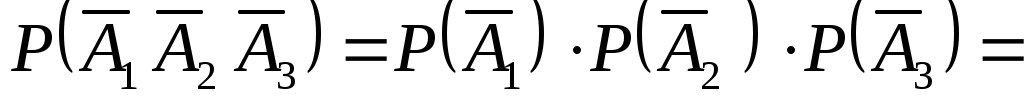
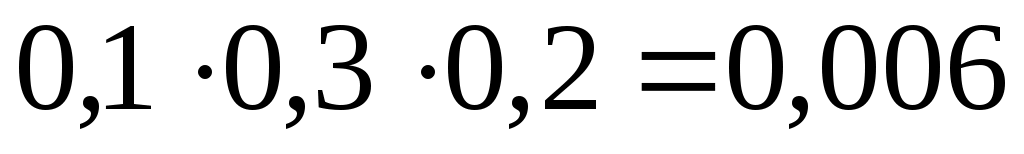 .
.
Итак,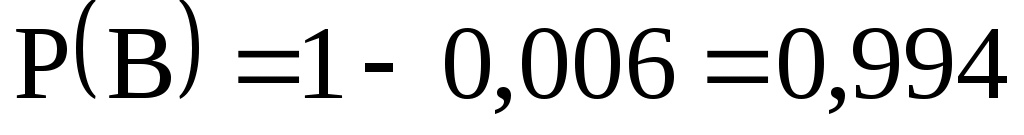 .
.
г) Событие Г={студент ответил по крайней мере на два вопроса}. Это означает, что дан ответ на любые два вопроса или на все три вопроса. Появление события Г означает, что наступило одно из четырёх несовместных событий: либо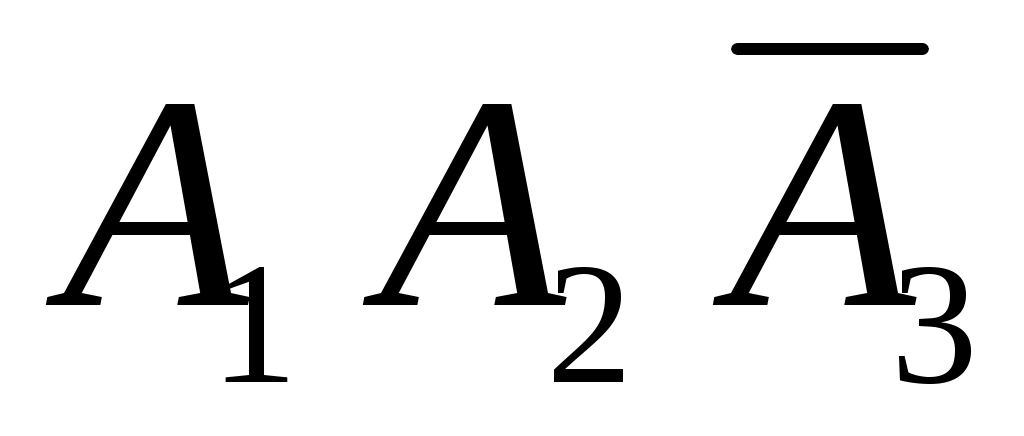 , либо
, либо 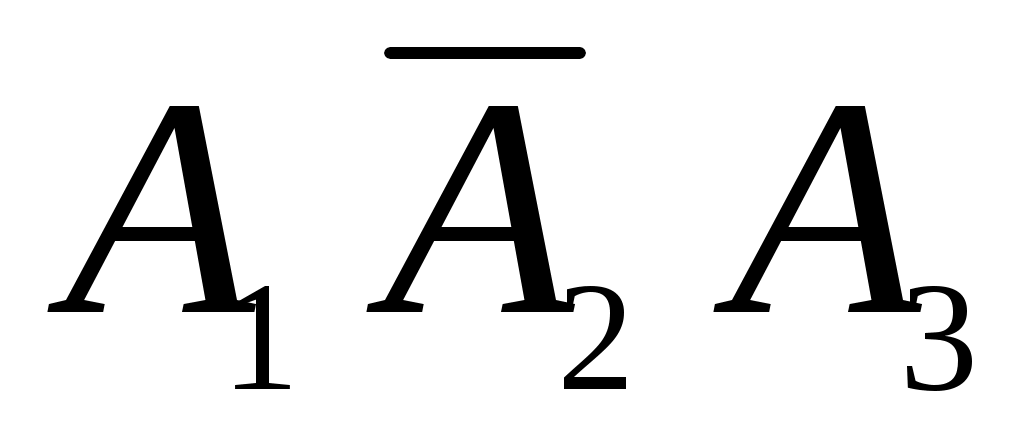 , либо
, либо 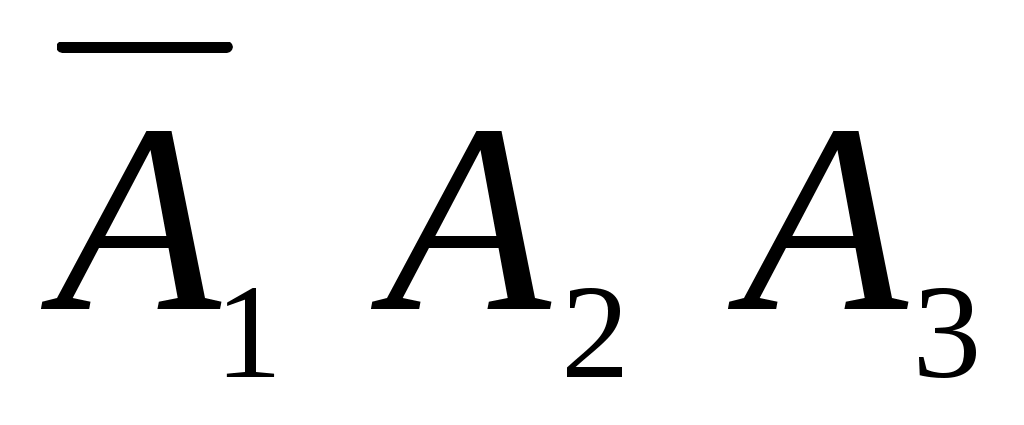 , либо
, либо 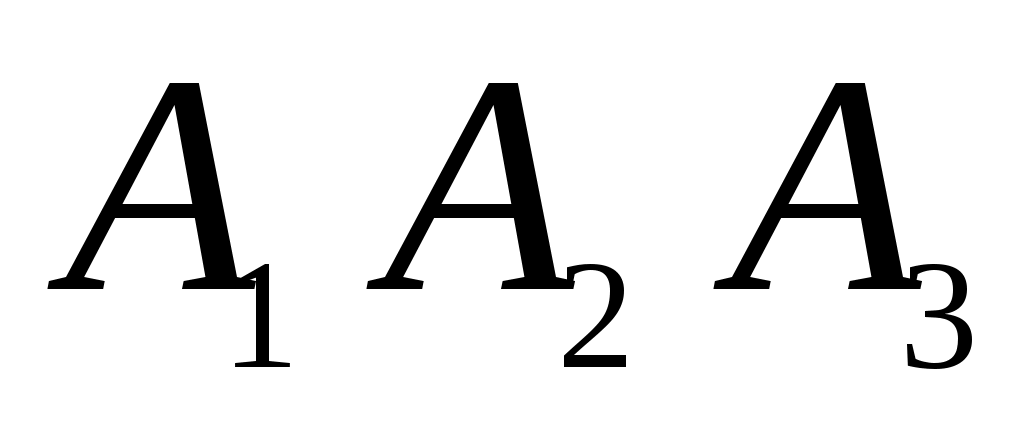 . По правилу сложения вероятностей несовместных событий
. По правилу сложения вероятностей несовместных событий
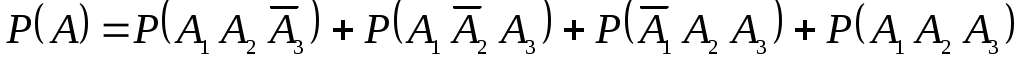 .
.
События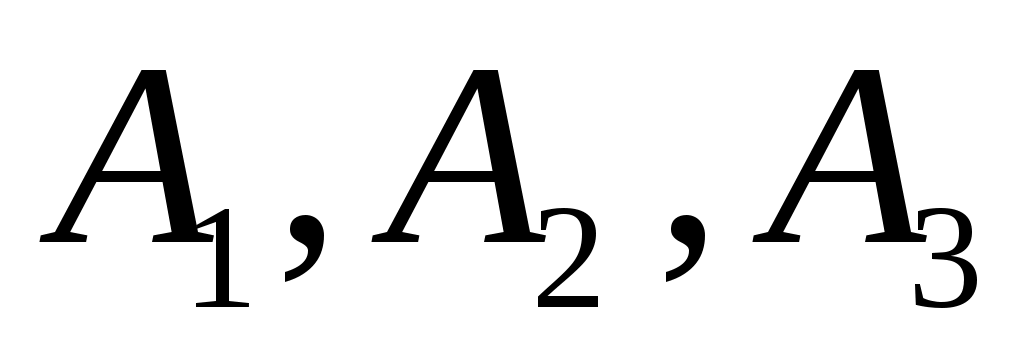 - независимые, следовательно, независимы события
- независимые, следовательно, независимы события 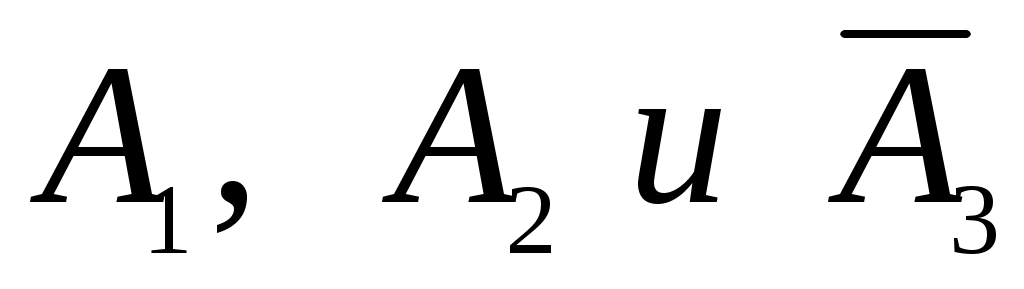 . По правилу умножения вероятностей независимых событий
. По правилу умножения вероятностей независимых событий
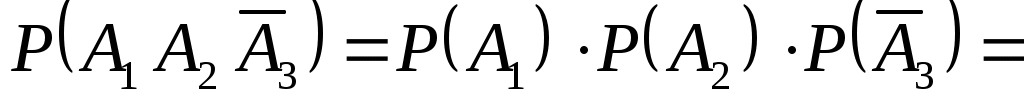
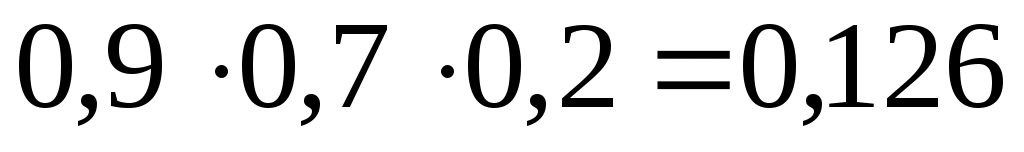 .
.
Аналогично получаем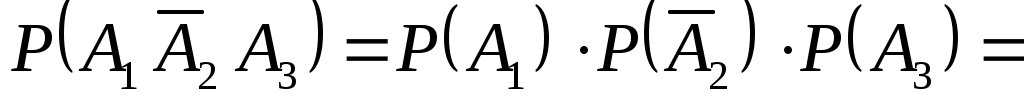
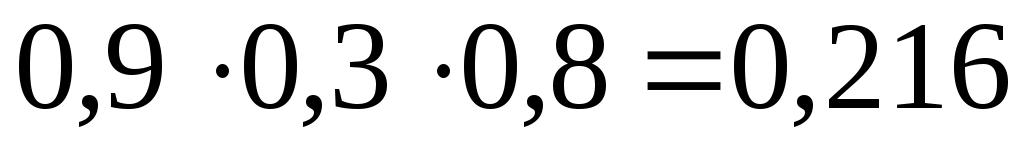 ,
,
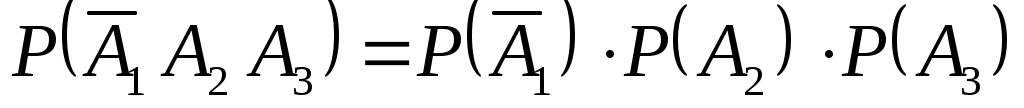
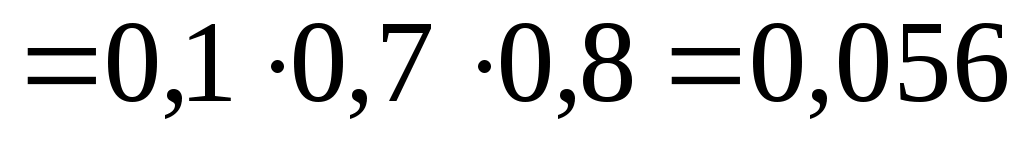 ,
,
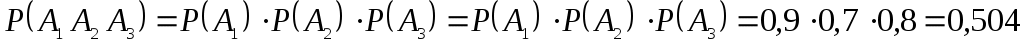 . Окончательно имеем
. Окончательно имеем 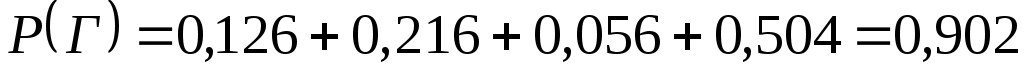 .
.
д) Событие Д={ студент ответил на два вопроса }. Появление события Д означает, что наступило одно из трёх несовместных событий: либо
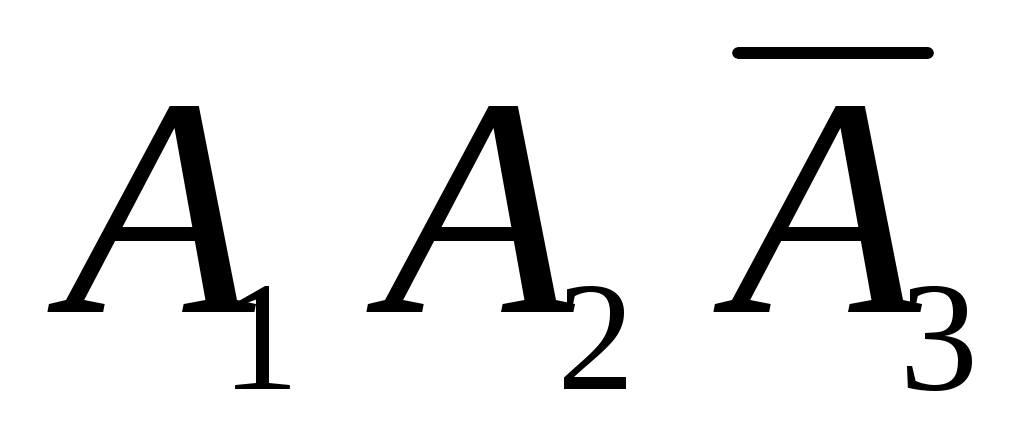 , либо
, либо  , либо
, либо 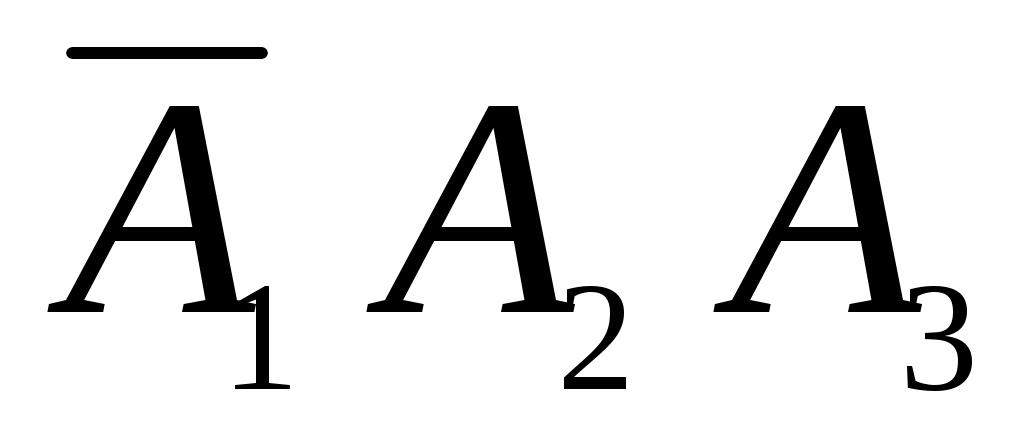 . Далее, используя решение задачи г), имеем
. Далее, используя решение задачи г), имеем 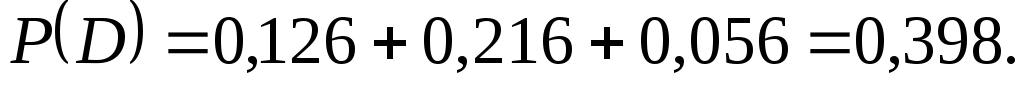
Тема 3. Формула полной вероятности. Формулы Бейеса
Пусть событие А может наступить лишь при появлении одного из множества попарно несовместных событий (гипотез) H1, H 2 , …, Hn . Тогда вероятность события А вычисляется по формуле полной вероятности .
.
События H1, H 2 , …, Hn называются гипотезами по отношению к событию А.
Если событие А уже произошло, то вероятности гипотез (априорные вероятности) могут быть переоценены (апостериорные вероятности) по формулам Бейеса
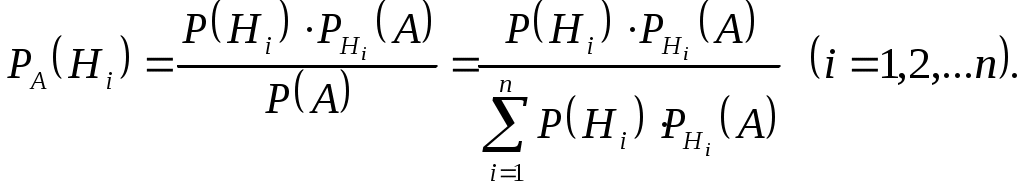
Пример 5. (Варианты 2, 4, 6, 8)
В ателье имеются 5 плейеров, выпущенных заводом B, 10 плейеров – заводом C, 15 плейеров – заводом D. Вероятность того, что плейеры, выпущенные заводами B, С, D, выдержат гарантийный срок службы, соответственно равны 0,8, 0,85 и 0,9. Найти вероятность того, что взятый наудачу плейер выдержит гарантийный срок службы.
Решение:
Событие А = {плейер выдержит гарантийный срок службы},
Гипотеза H1 = {плейер выпущен заводом В},
Гипотеза H2 = {плейер выпущен заводом С},
Гипотеза H3 = {плейер выпущен заводом D}.
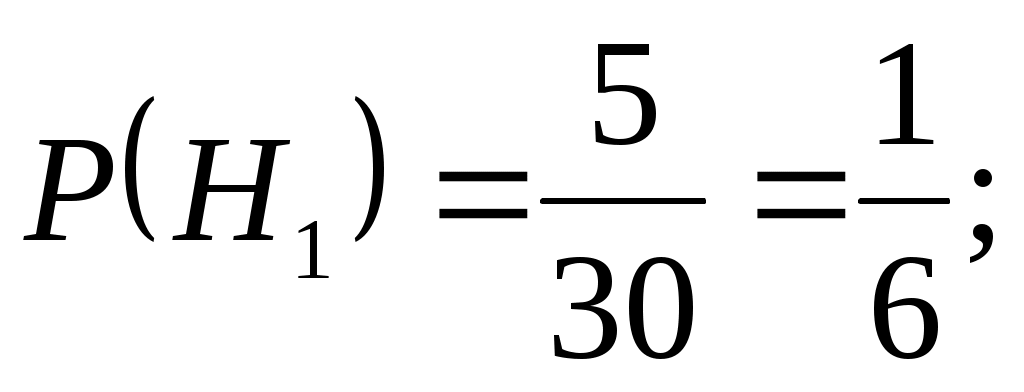
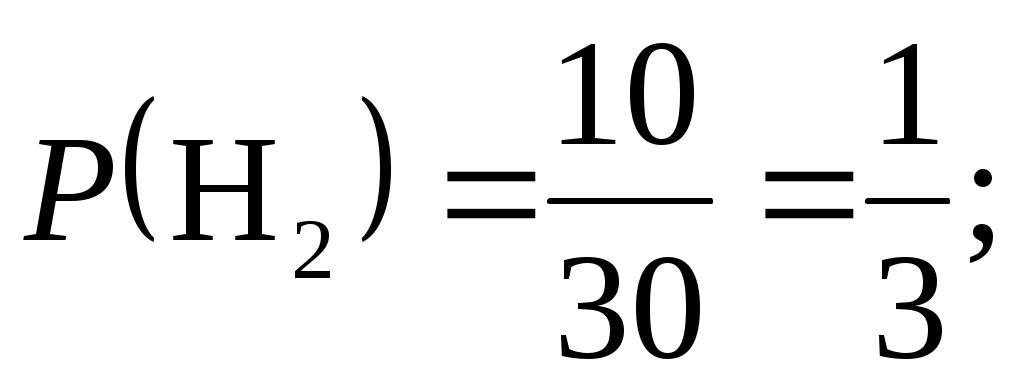
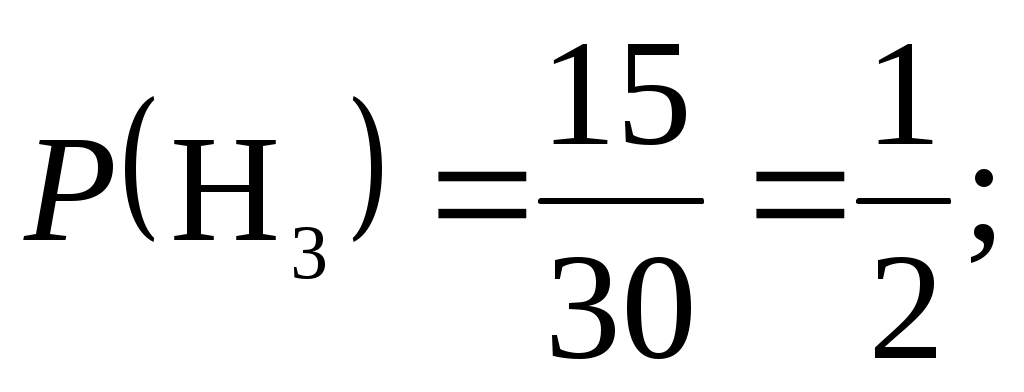
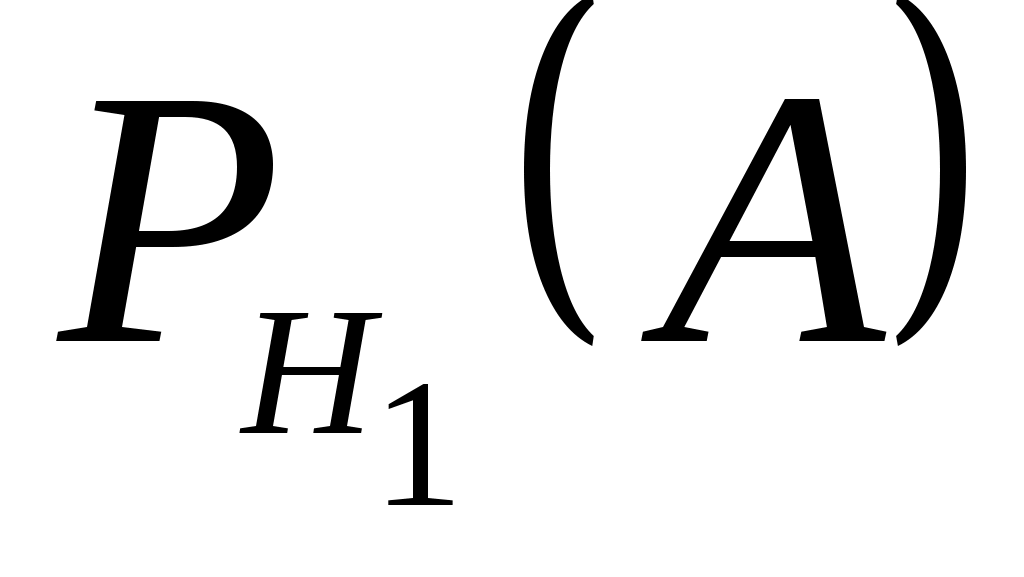 =0,8;
=0,8; 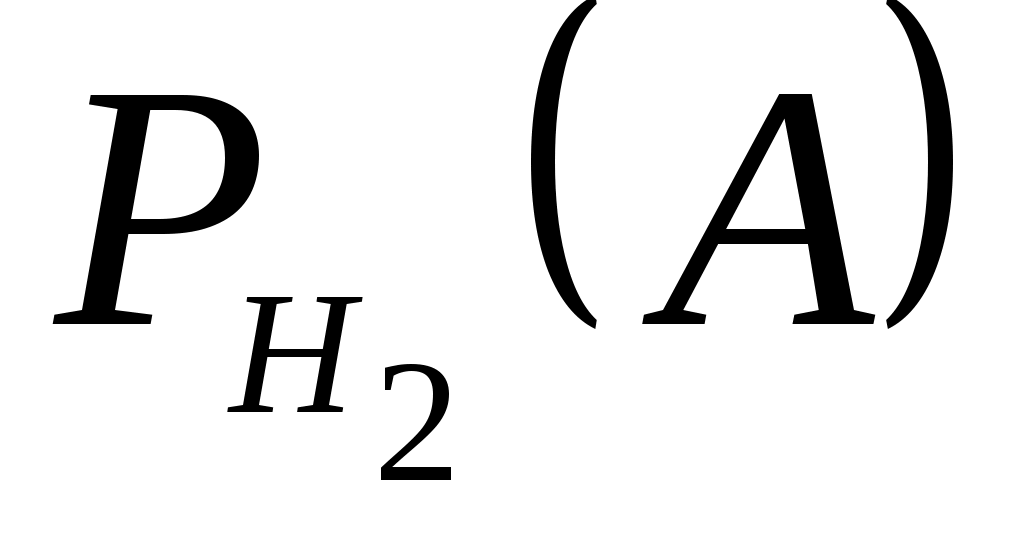 =0,85;
=0,85; 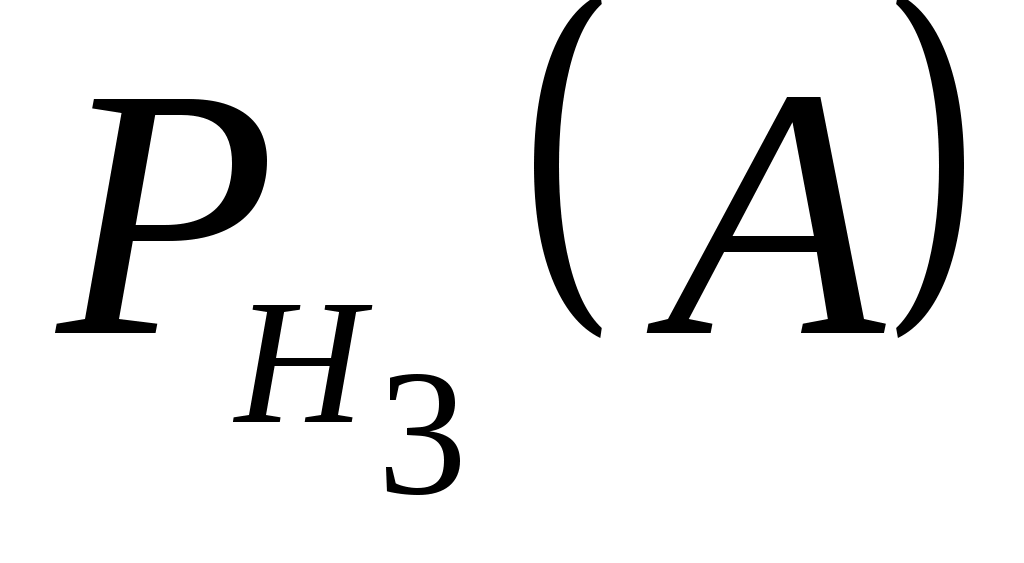
Правила сложения и умножения вероятностей
События называются несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.
Два события называются совместными, если появление одного из них не исключает появление другого события в том же испытании.
Событие В называется независимым от события А, если появление события А не изменяет вероятности события В, т.е.
1. Сложение вероятностей.
Правило сложения вероятностей совместных событий
Для любых событий А и В
Р(А+В)=Р(А)+Р(В)-Р(АВ), где
Р(А+В) – вероятность появления хотя бы одного из двух событий,
Р(АВ) – вероятность совместного появления двух событий.
Правило сложения вероятностей несовместных событий
Р(А+В)=Р(А)+Р(В).
2. Умножение вероятностей
Правило умножения вероятностей зависимых событий
Для любых событий А и В
Правило умножения вероятностей независимых событий
Пример 4. (Все варианты)
Экзаменационный билет содержит 3 вопроса. Вероятность того, что студент ответит на первый вопрос, рана 0,9; на второй – 0,7; на третий – 0,8. Найти вероятность того, что студент ответит:
а) только на один вопрос (варианты 1,2,3,7,10)
б) на все вопросы (варианты 7,8)
в) хотя бы на один вопрос (варианты 3,4,6)
г) по крайней мере на два вопроса (варианты 3,9)
д) на два вопроса (варианты 4,5)
Решение:
Пусть событие
= {студент ответил на первый вопрос},
События
а) Событие
Появление события А означает, что наступило одно из трёх несовместных событий: либо
. События
Аналогично
Тогда
б) Событие Б={студент ответил на все вопросы}. Наступление события Б означает, что одновременно появились независимые события
в) Событие В ={ студент ответил хотя бы на один вопрос }. Это означает, что был дан ответ на любой один вопрос, или на любые два вопроса, или на все три вопроса. Событие
, т. е.
Итак,
г) Событие Г={студент ответил по крайней мере на два вопроса}. Это означает, что дан ответ на любые два вопроса или на все три вопроса. Появление события Г означает, что наступило одно из четырёх несовместных событий: либо
События
Аналогично получаем
д) Событие Д={ студент ответил на два вопроса }. Появление события Д означает, что наступило одно из трёх несовместных событий: либо
Тема 3. Формула полной вероятности. Формулы Бейеса
-
Формула полной вероятности
Пусть событие А может наступить лишь при появлении одного из множества попарно несовместных событий (гипотез) H1, H 2 , …, Hn . Тогда вероятность события А вычисляется по формуле полной вероятности
 .
.События H1, H 2 , …, Hn называются гипотезами по отношению к событию А.
-
Формулы Бейеса
Если событие А уже произошло, то вероятности гипотез (априорные вероятности) могут быть переоценены (апостериорные вероятности) по формулам Бейеса
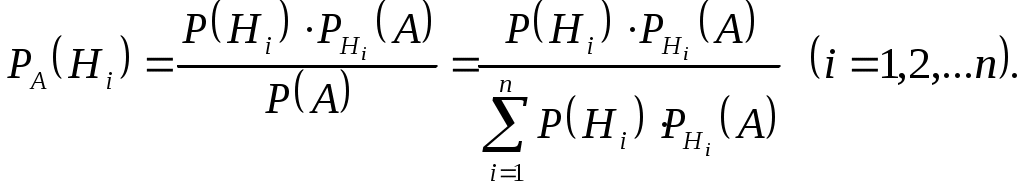
Пример 5. (Варианты 2, 4, 6, 8)
В ателье имеются 5 плейеров, выпущенных заводом B, 10 плейеров – заводом C, 15 плейеров – заводом D. Вероятность того, что плейеры, выпущенные заводами B, С, D, выдержат гарантийный срок службы, соответственно равны 0,8, 0,85 и 0,9. Найти вероятность того, что взятый наудачу плейер выдержит гарантийный срок службы.
Решение:
Событие А = {плейер выдержит гарантийный срок службы},
Гипотеза H1 = {плейер выпущен заводом В},
Гипотеза H2 = {плейер выпущен заводом С},
Гипотеза H3 = {плейер выпущен заводом D}.