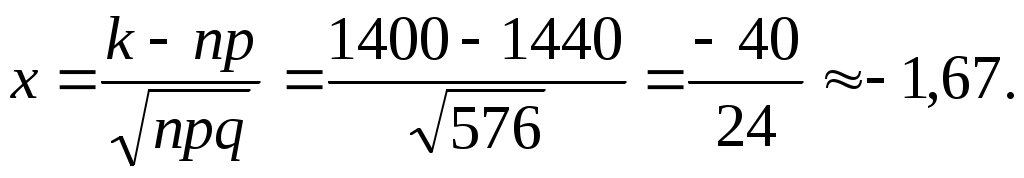Файл: Методические рекомендации по выполнению контрольной работы по дисциплине Высшая математика.doc
Добавлен: 09.12.2023
Просмотров: 161
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
=0,9.
По формуле полной вероятности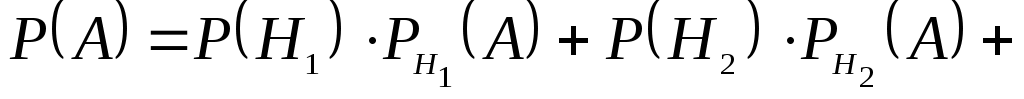
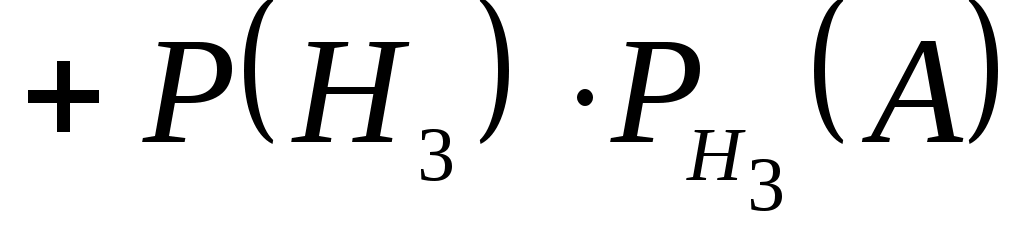
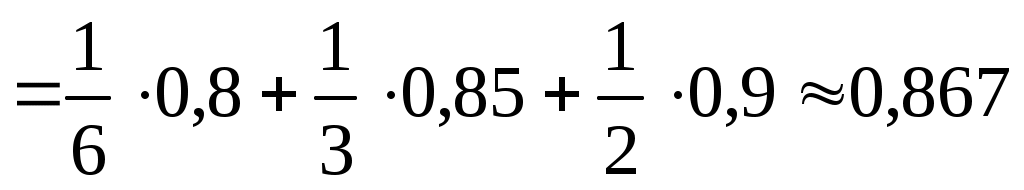 .
.
Пример 6. (Варианты 1, 3, 5, 7, 9, 10)
Литьё в болванках поступает из двух заготовительных цехов: 70% из первого цеха, 30% из второго цеха. Литьё первого цеха имеет 10% брака, второго – 20% брака. Взятая наудачу болванка оказалась без дефекта. Какова вероятность её изготовления первым цехом?
Решение:
Событие А ={болванка без дефекта}.
Гипотеза H1 – болванка изготовлена первым цехом,
Гипотеза H2 – болванка изготовлена вторым цехом,
Литьё первого цеха имеет 10% брака, следовательно, 90% болванок, изготовленных первым цехом, не имеют дефекта и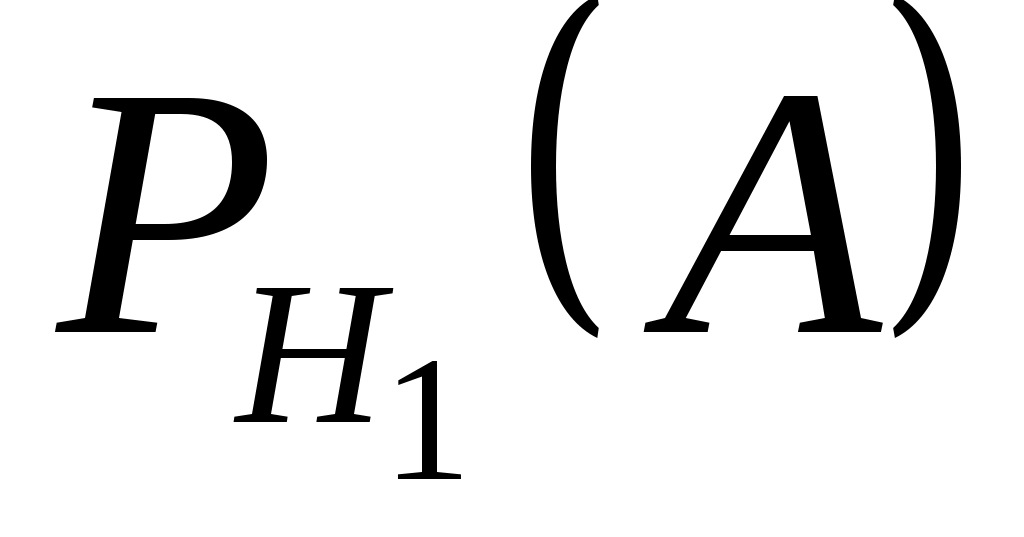 =0,9. Литьё второго цеха имеет 20% брака, следовательно, 80% болванок, изготовленных вторым цехом, не имеют дефекта и
=0,9. Литьё второго цеха имеет 20% брака, следовательно, 80% болванок, изготовленных вторым цехом, не имеют дефекта и 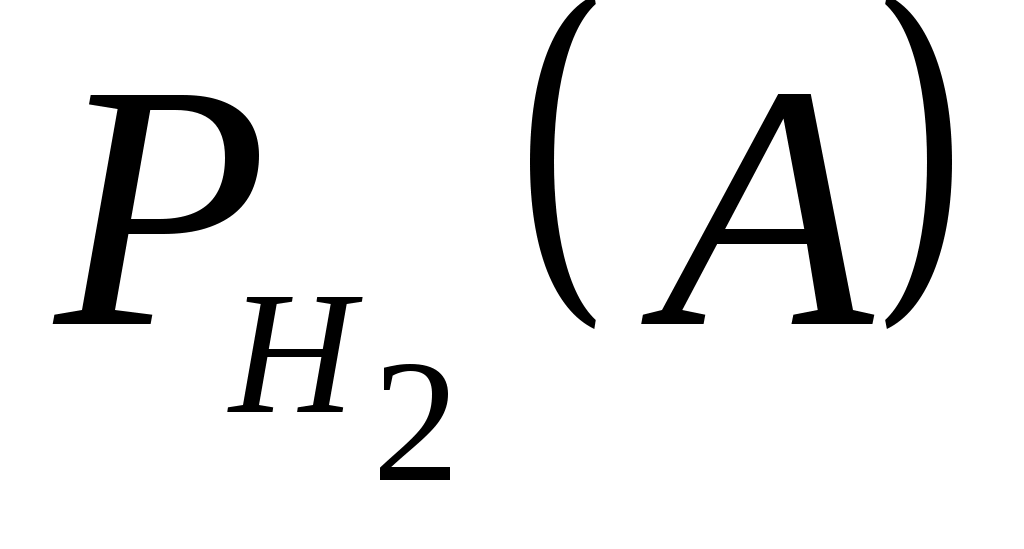 =0,8. Необходимо найти
=0,8. Необходимо найти 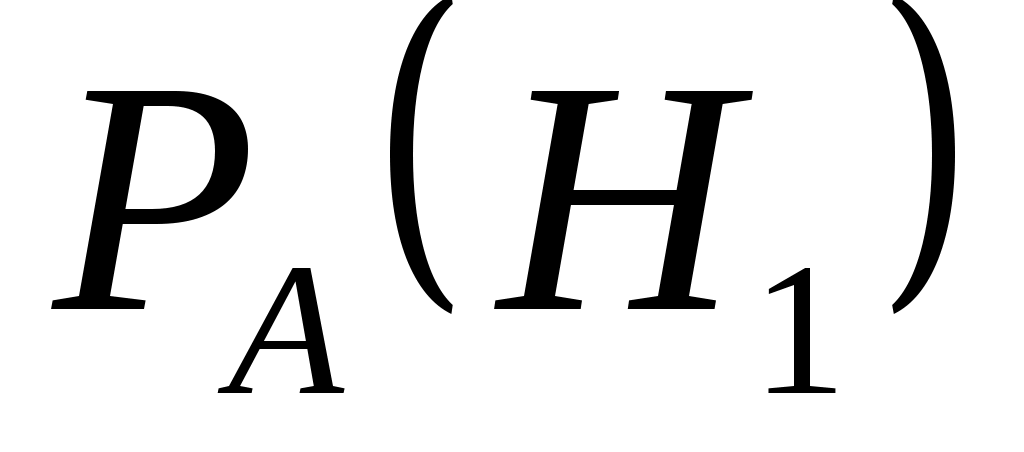 .
.
По формуле Бейеса
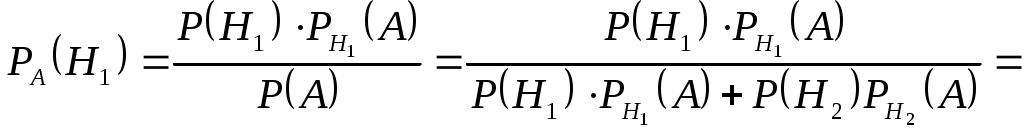
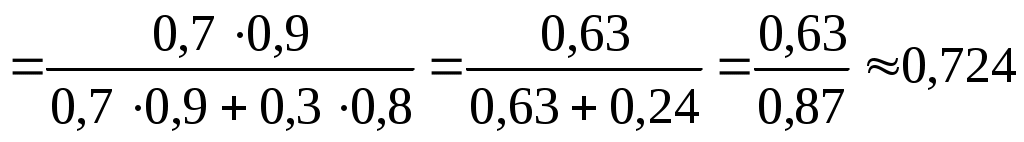 .
.
Тема 4. Повторение независимых испытаний.
Вероятность того, что в серии из п независимых испытаниях, в каждом из которых вероятность появления события A равна p (0р1), это событие наступит ровно k раз (безразлично в какой последовательности), равна
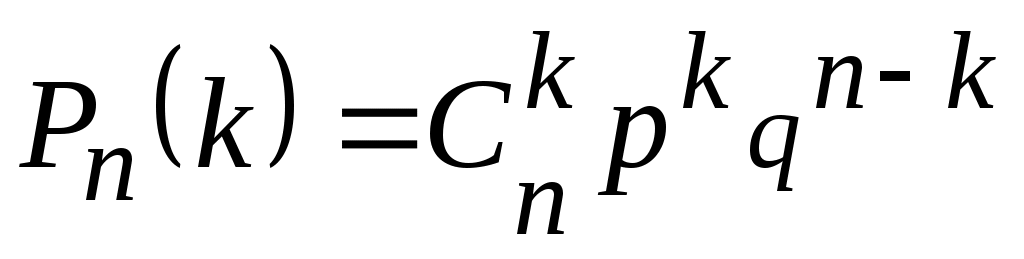 ,
,
где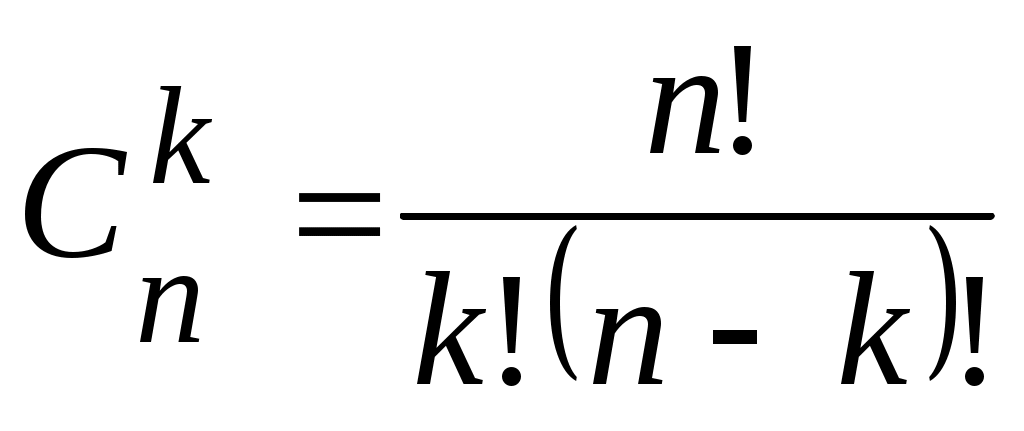 – число сочетаний из n по k (см. выше), q=1-p– вероятность противоположного события
– число сочетаний из n по k (см. выше), q=1-p– вероятность противоположного события  .
.
В различных задачах нас могут интересовать следующие вероятности:
– вероятность того, что в п испытаниях событие A наступит менее m раз
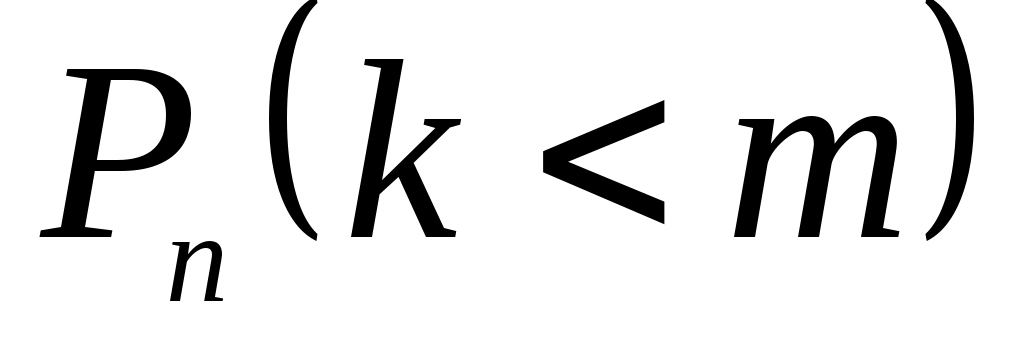
=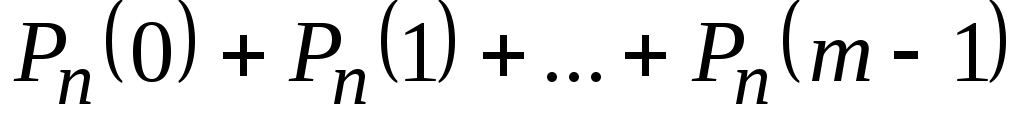 ;
;
– вероятность того, что в п испытаниях событие A наступит более m раз
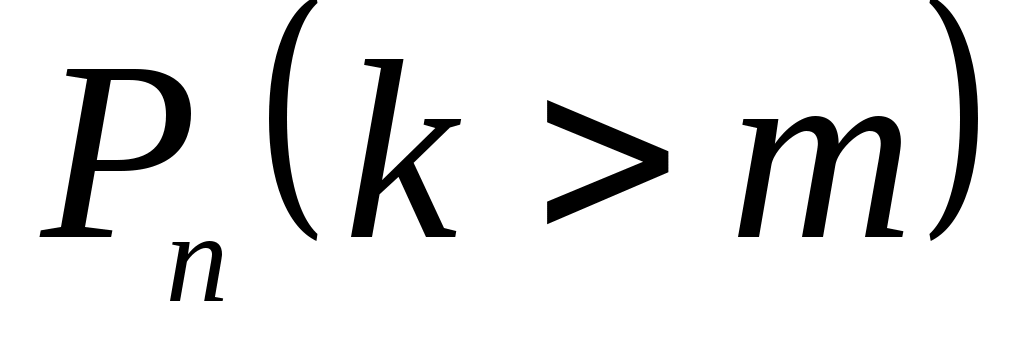 =
=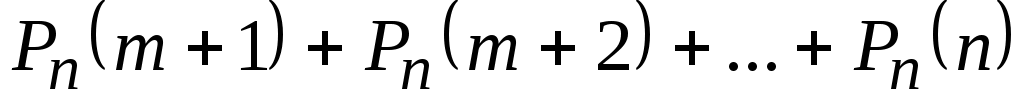 ;
;
– вероятность того, что в п испытаниях событие A наступит не менее m раз
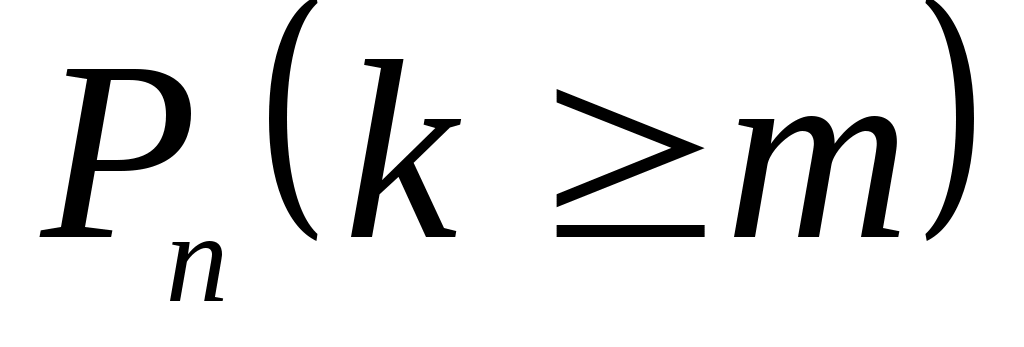 =
=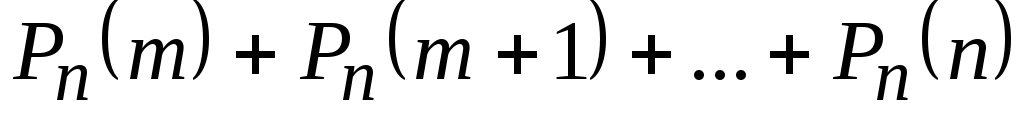 ;
;
– вероятность того, что в п испытаниях событие A наступит не более m раз
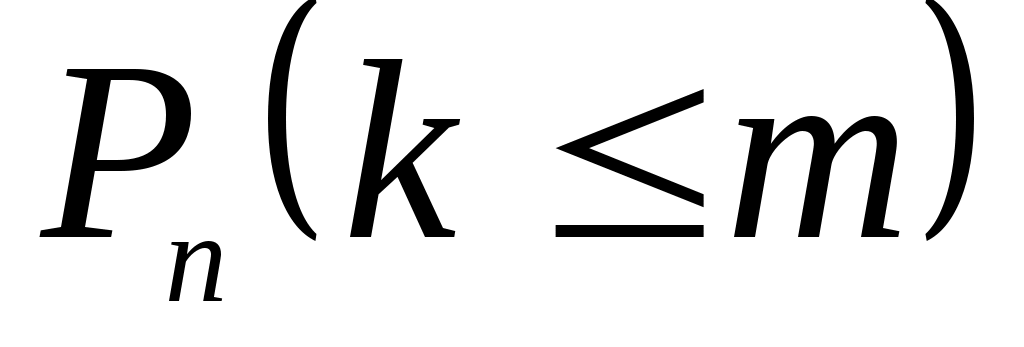 =
=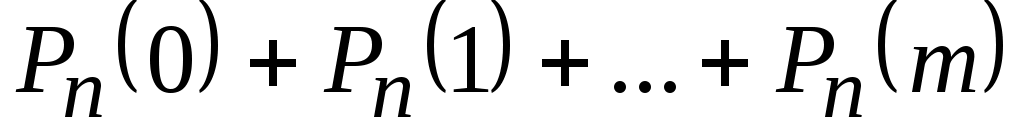 .
.
– вероятность того, что в п испытаниях событие A наступит не менее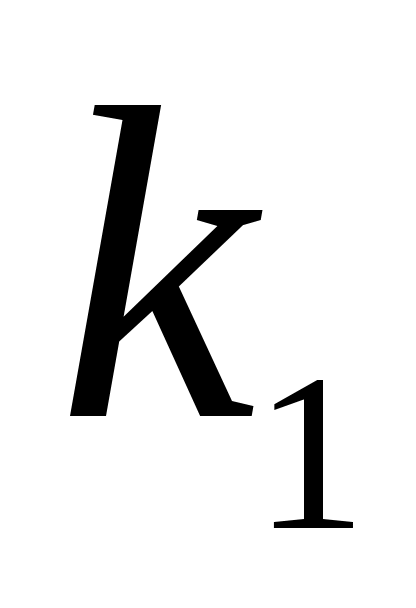 и не более
и не более 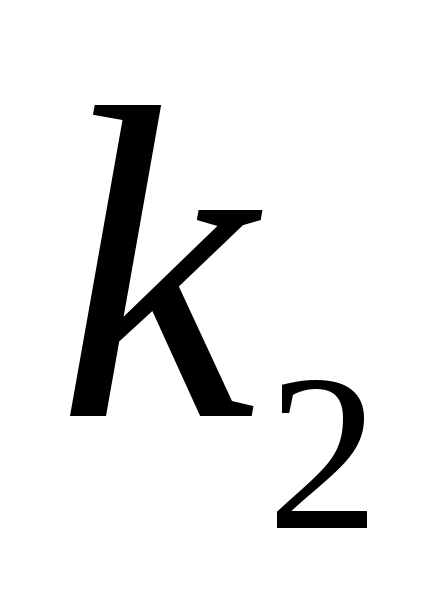 раз
раз
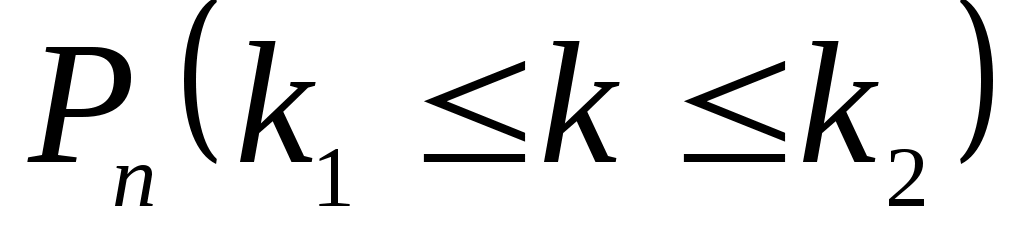 =
=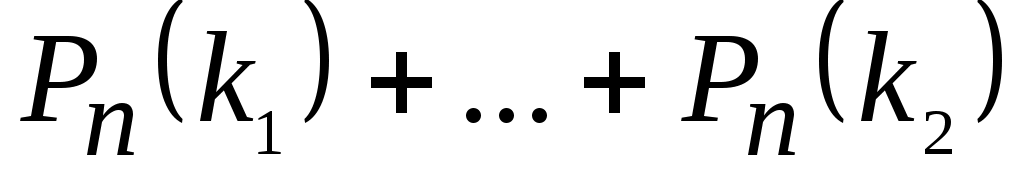 .
.
Все эти вероятности могут быть вычислены по формуле Бернулли, однако, на практике ввиду вычислительных сложностей это возможно лишь при небольших n и поэтому используются приближенные формулы.
2.1. Локальная теорема Лапласа
Если число испытаний n велико, а вероятность p не очень мала, то
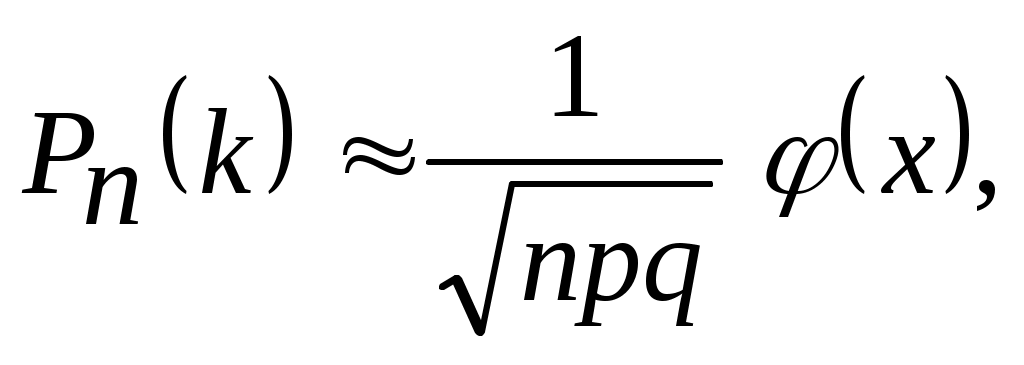
где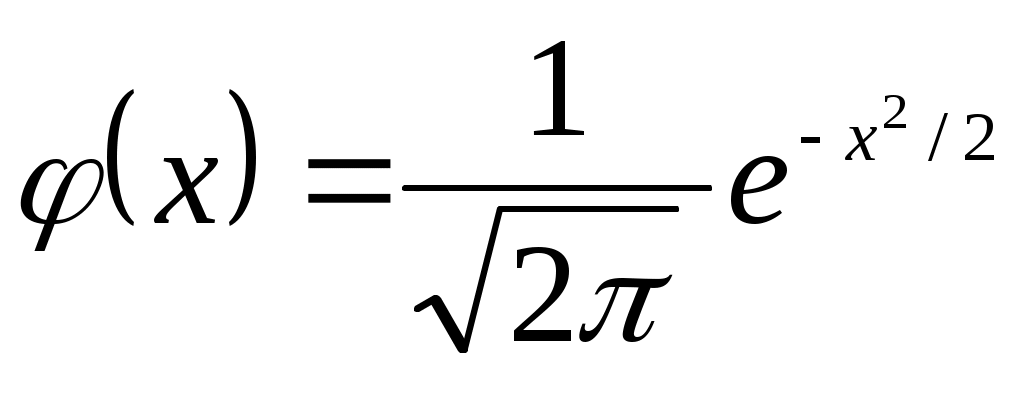 ,
, 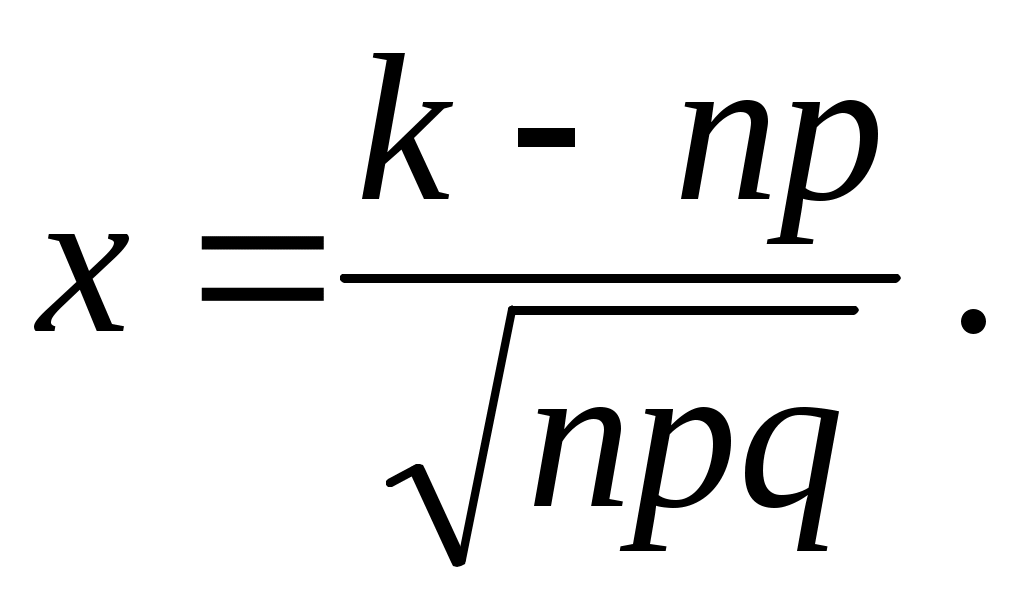
Значения функции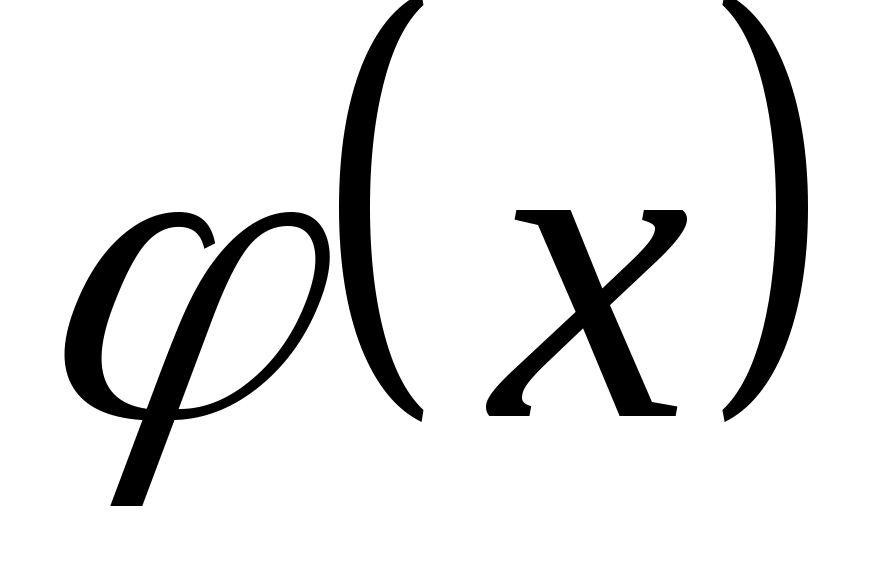 приведены в приложении (таблица 1), при
приведены в приложении (таблица 1), при  полагают
полагают 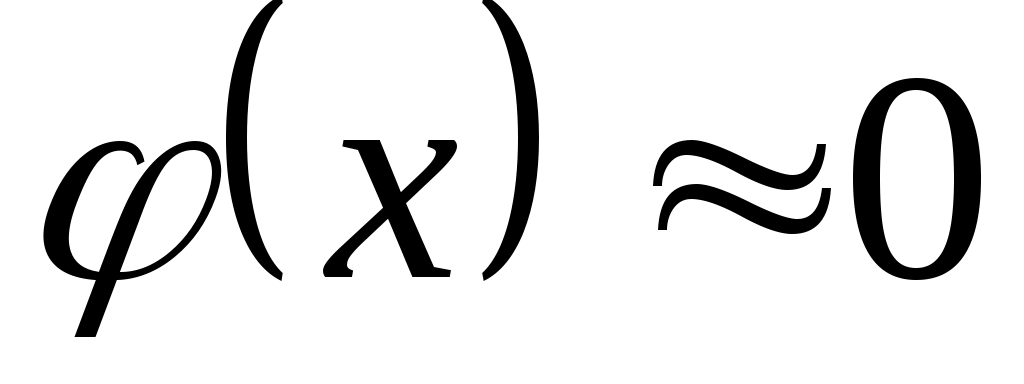 , для отрицательных значений x пользуются тем, что функция
, для отрицательных значений x пользуются тем, что функция 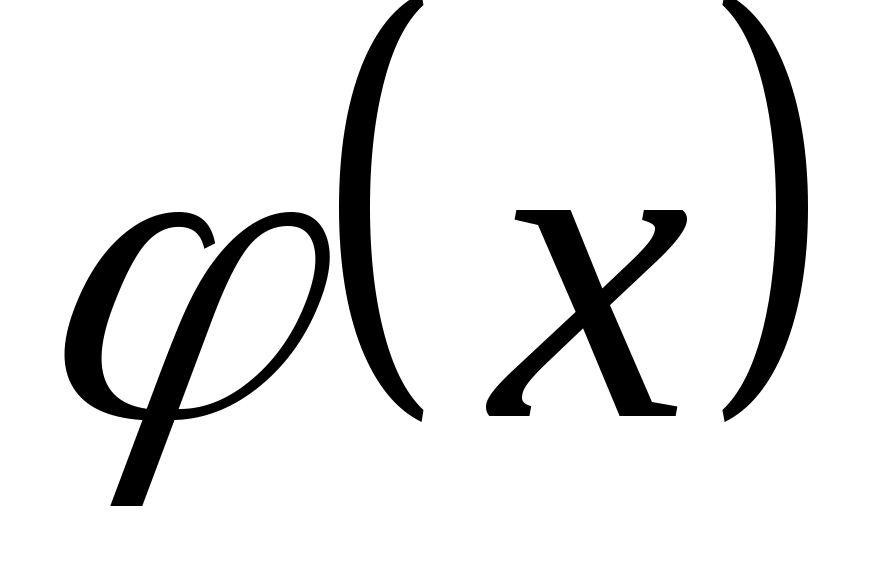
четная, и, следовательно,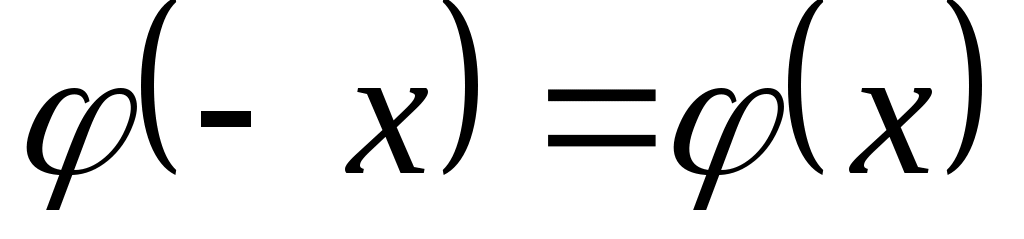 .
.
2.2. Интегральная теорема Лапласа
Вероятность того, что событие А появится в n испытаниях не менее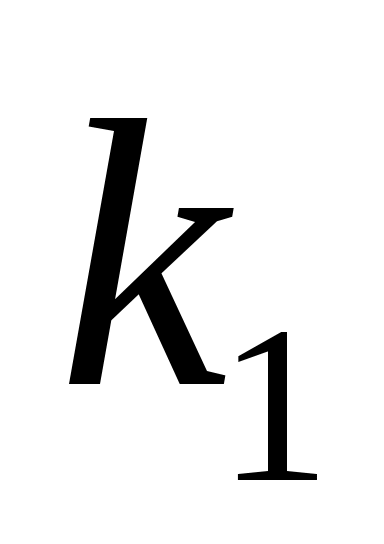 и не более
и не более 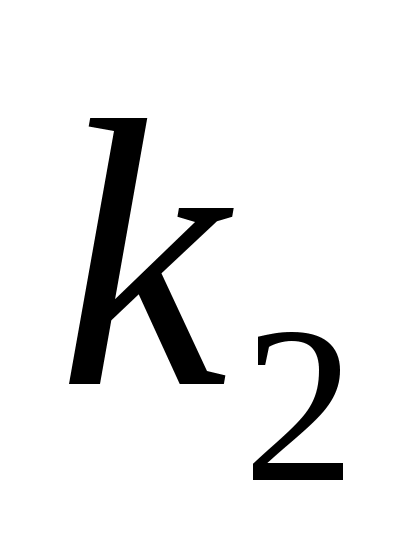 раз находится по формуле
раз находится по формуле
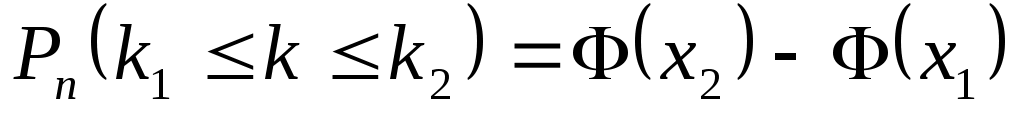 ,
,
где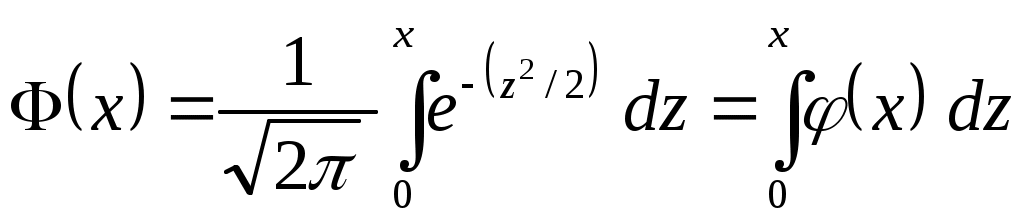 ,
, 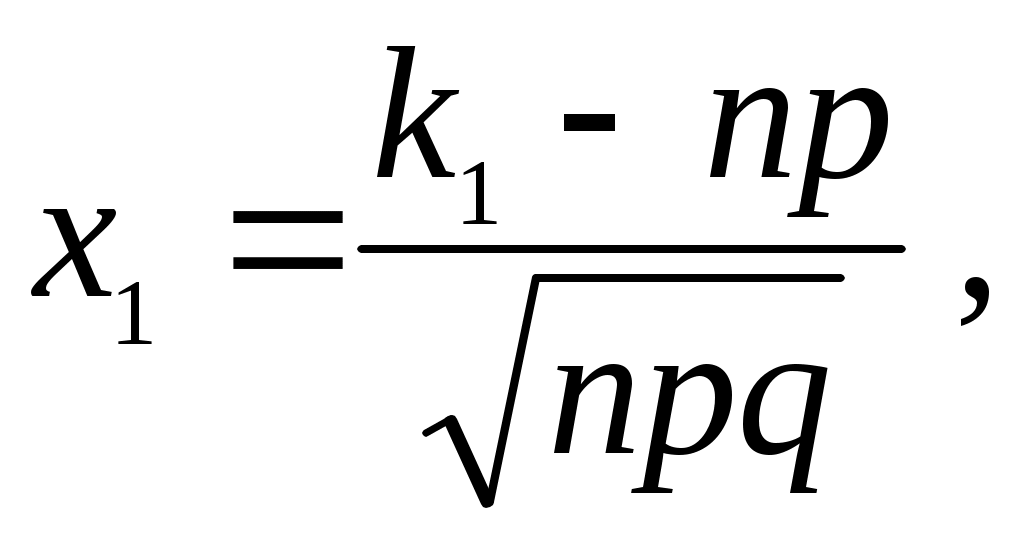
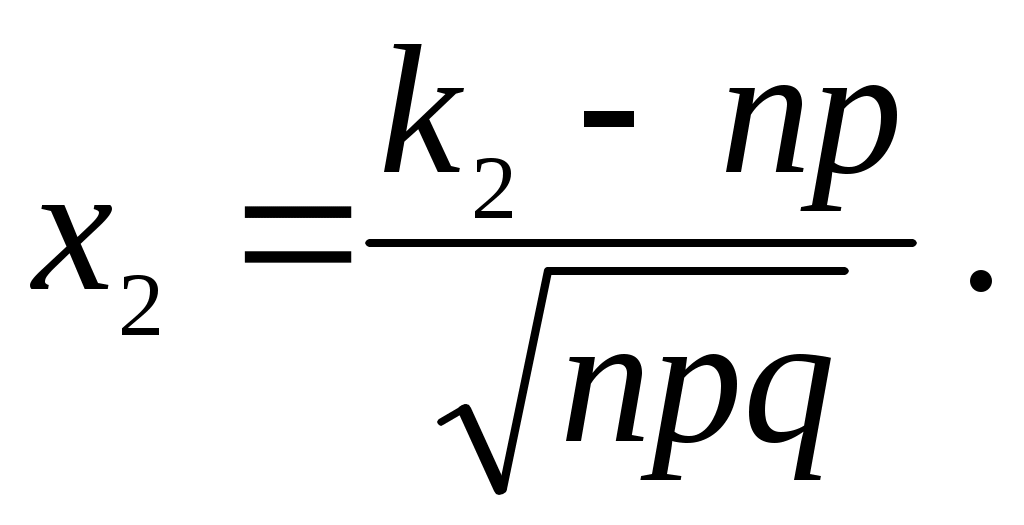
Значения функции Лапласа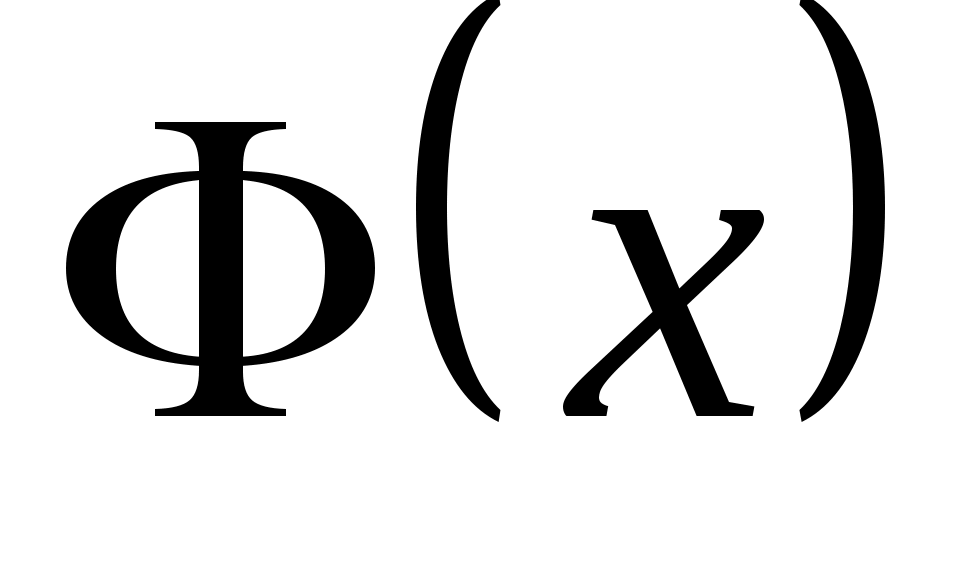 приведены в приложении (таблица 2), при
приведены в приложении (таблица 2), при  полагают
полагают 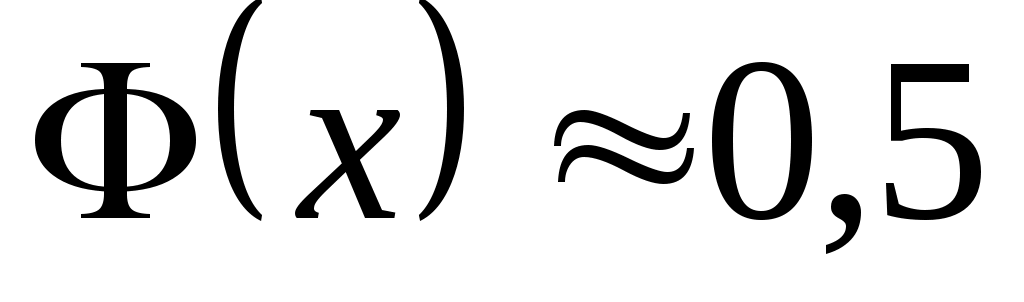 , для отрицательных значений x пользуются тем, что функция
, для отрицательных значений x пользуются тем, что функция 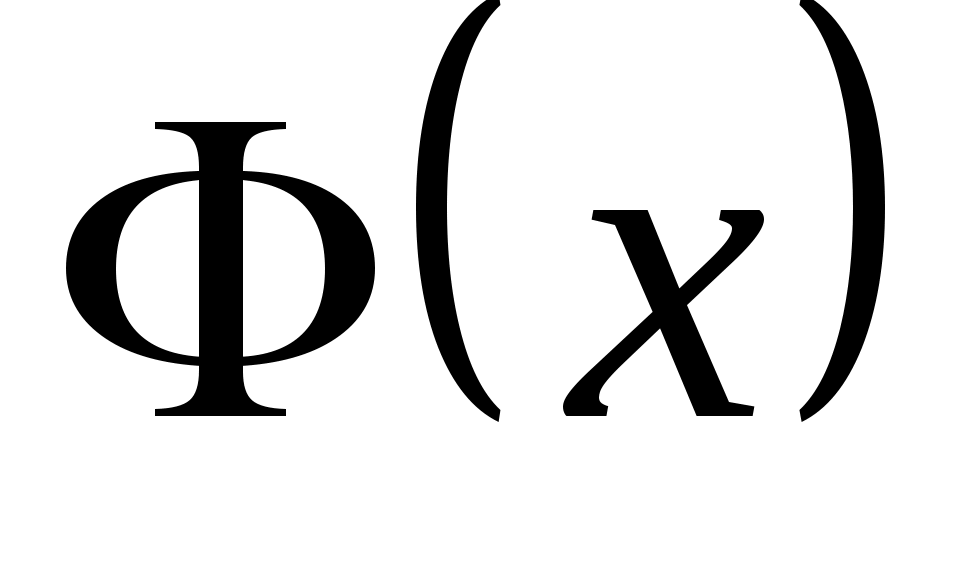 нечетная, и, следовательно,
нечетная, и, следовательно, 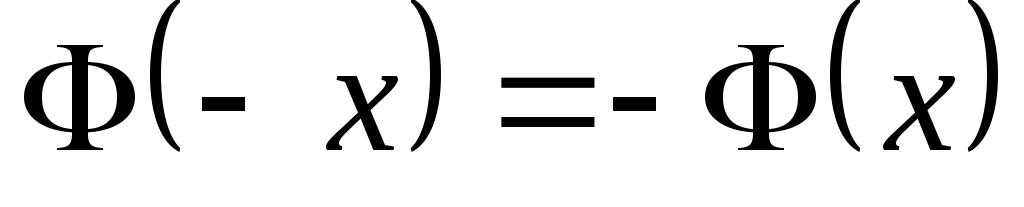 .
.
Если число испытаний n велико, а вероятность p появления события в каждом испытании очень мала, то
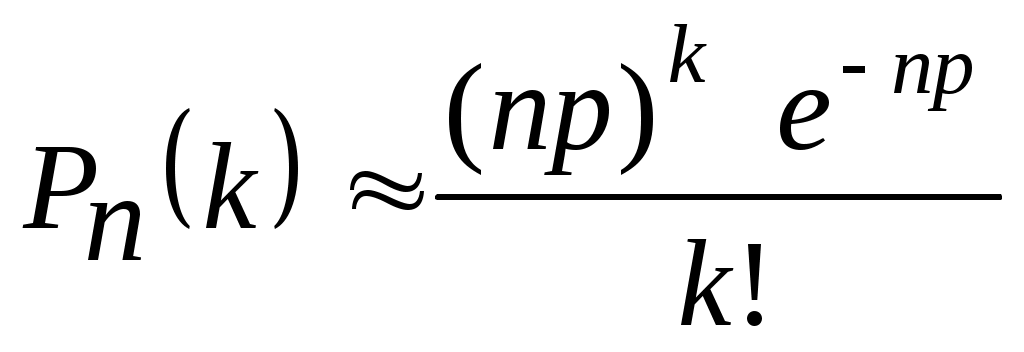 .
.
Обозначив , =np– среднее число успехов в серии испытаний, получим
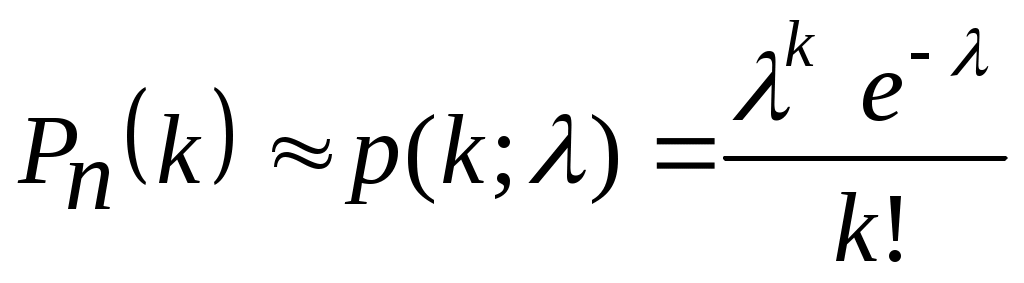 .
.
Значение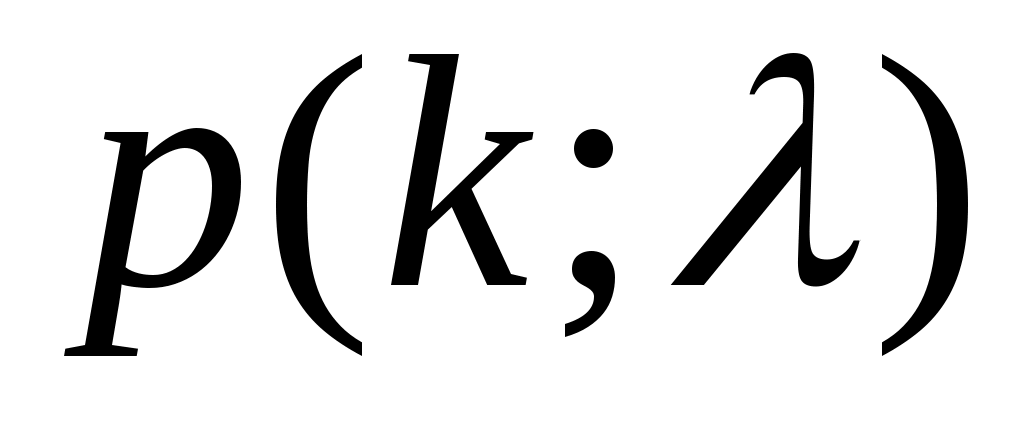 по заданным k и можно определить по приложению (таблица 3).
по заданным k и можно определить по приложению (таблица 3).
4. Наивероятнейшее число успехов
Число k0 называется наивероятнейшим, если вероятность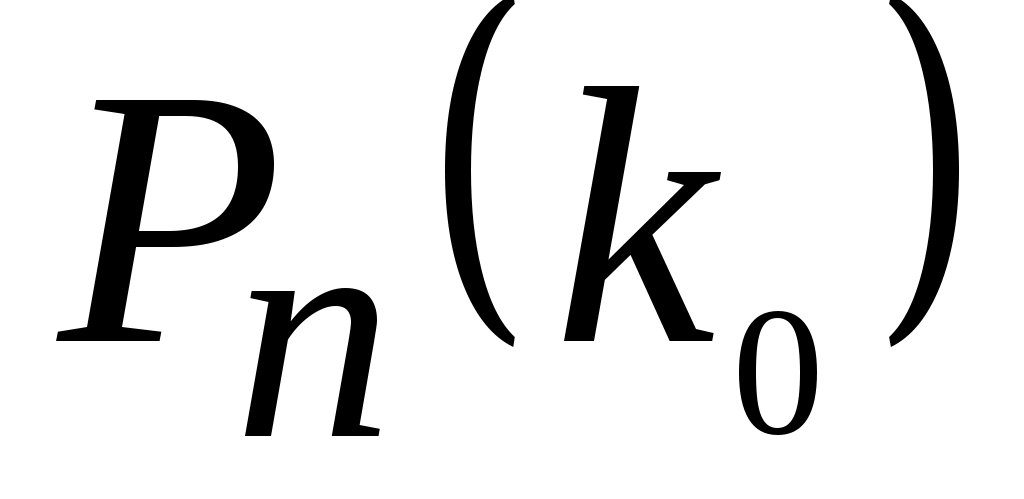 того, что событие A наступит в n испытаниях ровно k0 раз, является наибольшей из всех вероятностей
того, что событие A наступит в n испытаниях ровно k0 раз, является наибольшей из всех вероятностей 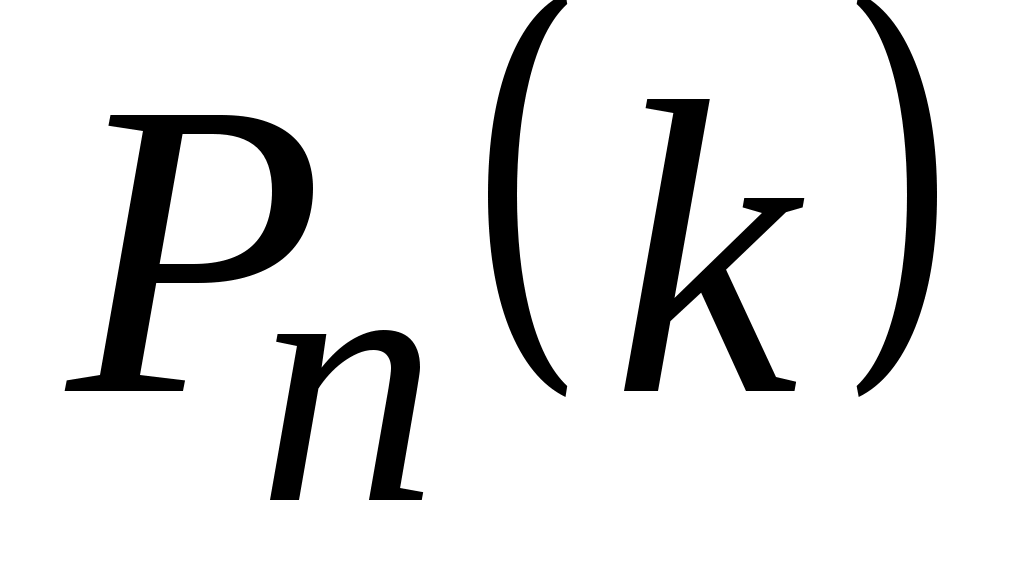 , k= 0, 1, … , n .
, k= 0, 1, … , n .
Наивероятнейшее число k0 определяется из двойного неравенства
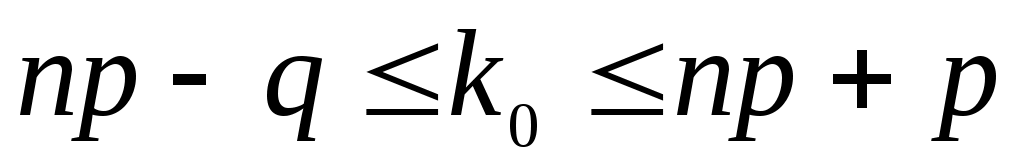 ,
,
причем:
а) если число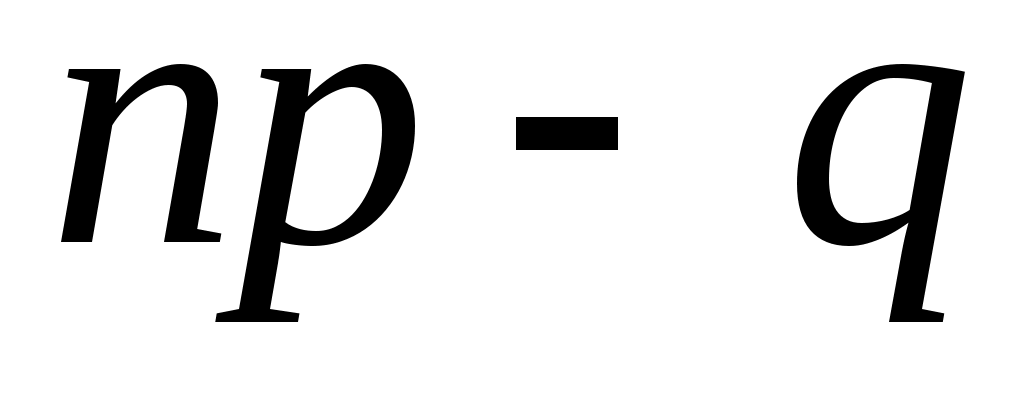 – нецелое, то существует единственное k0;
– нецелое, то существует единственное k0;
б) если число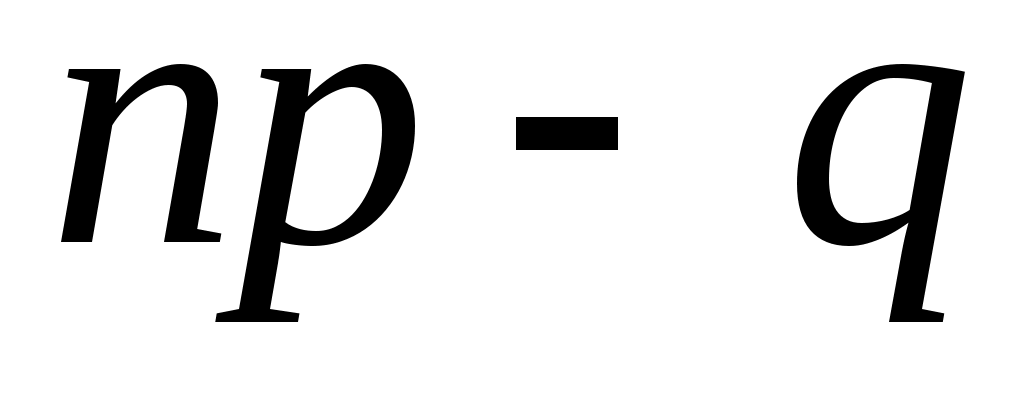 – целое, то наивероятнейших числа два, а именно:
– целое, то наивероятнейших числа два, а именно: 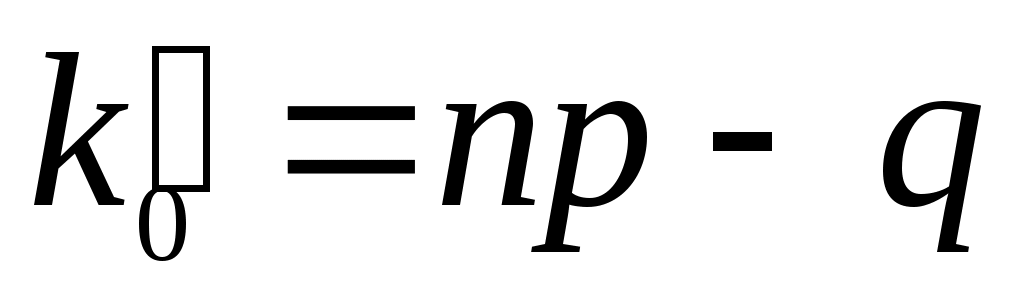 и
и 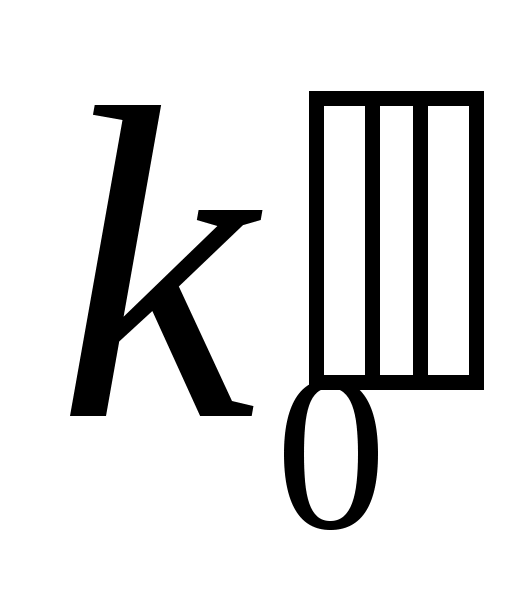 =
=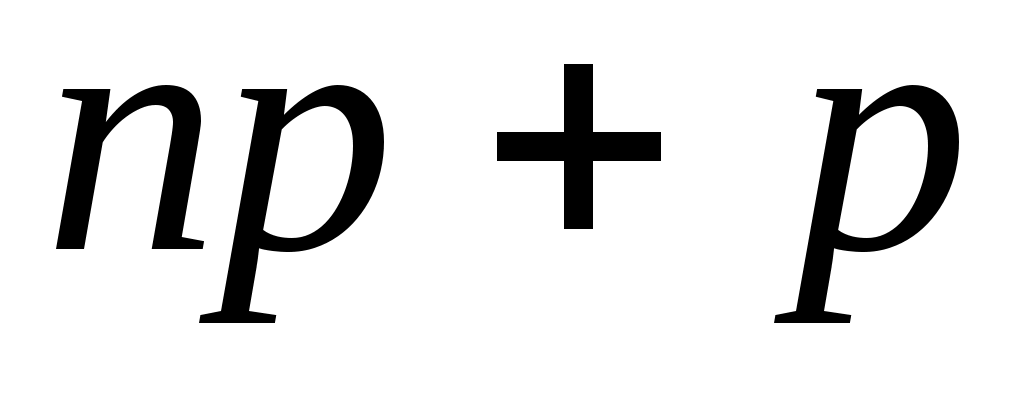 =
= 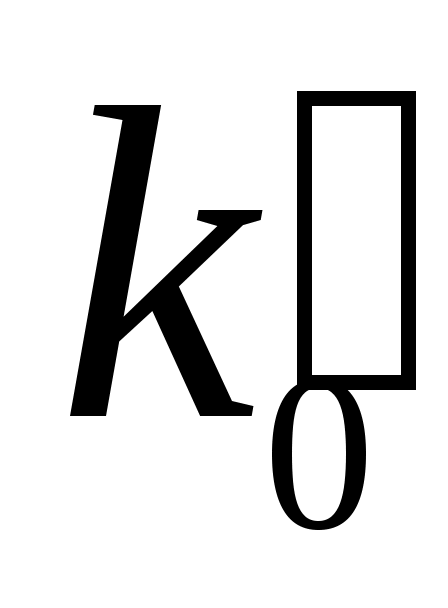 +1;
+1;
в) если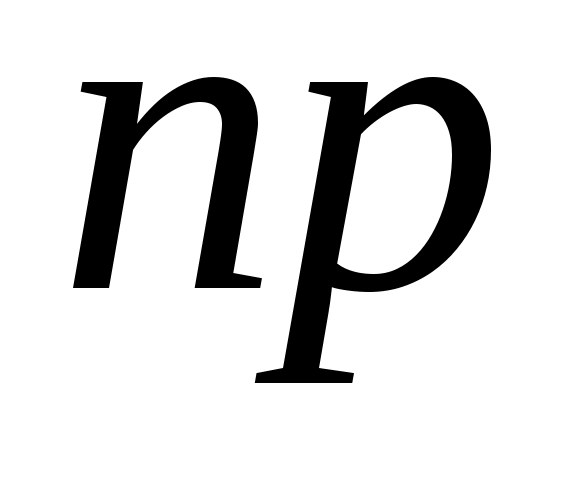 – целое, то
– целое, то 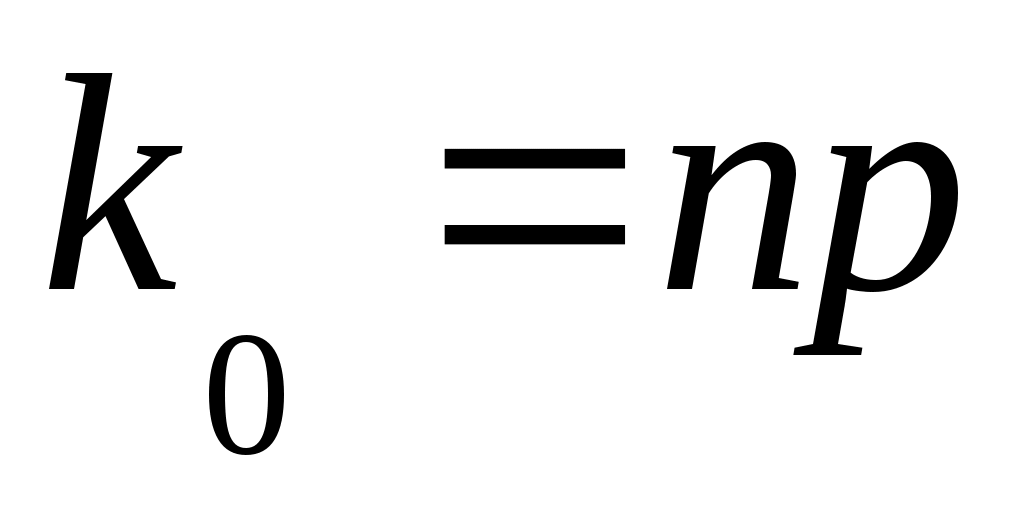 .
.
Пример 7. (Варианты 1, 7)
В семье пять детей. Найти вероятность того, что среди этих детей: а) ровно два мальчика; б) не более двух мальчиков; в) более двух мальчиков; г) не менее двух и не более трех мальчиков. Вероятность рождения мальчика принять равной 0,51.
Решение:
Число испытаний n=5 невелико, поэтому вероятности можно вычислить непосредственно по формуле Бернулли.
а) Вероятность того, что среди пяти детей ровно два мальчика, равна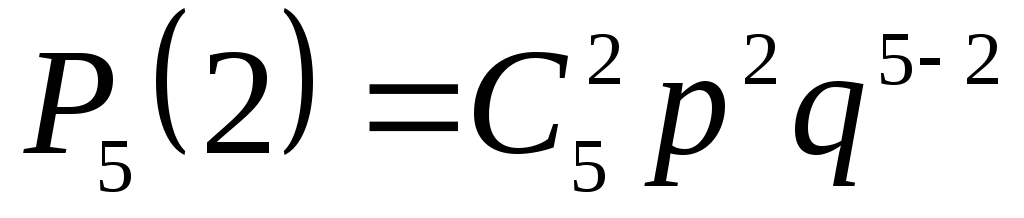 , где
, где 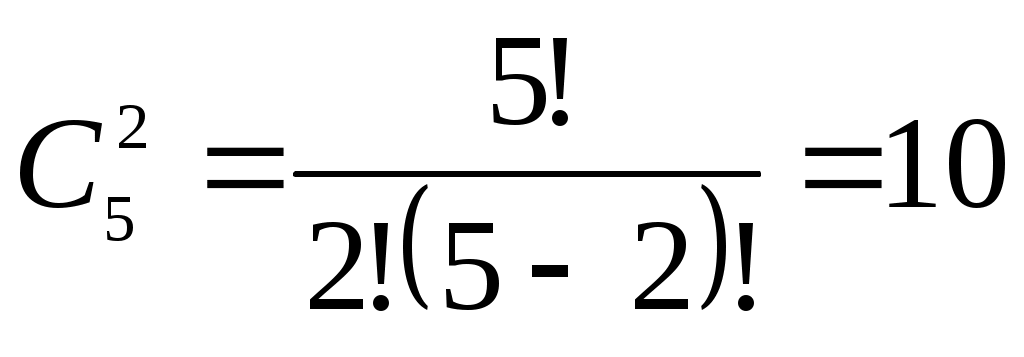 , p=0,51, q=1-p=0,49.
, p=0,51, q=1-p=0,49.
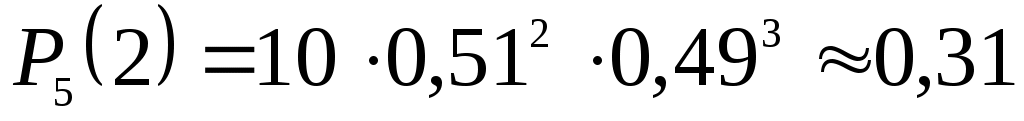 .
.
б) Вероятность того, что среди пяти детей не более двух мальчиков, равна
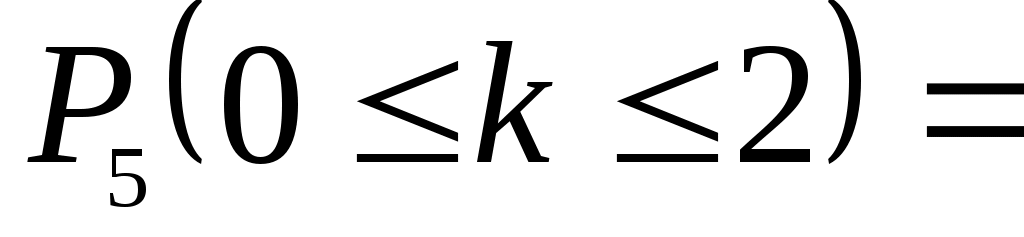
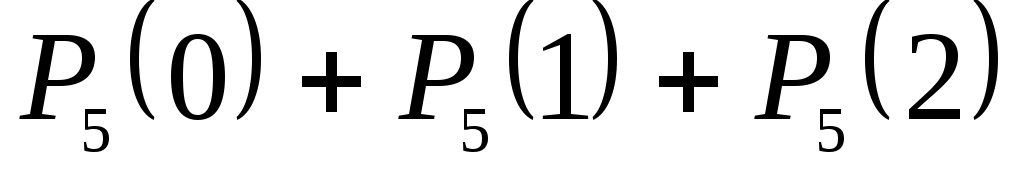 .
.
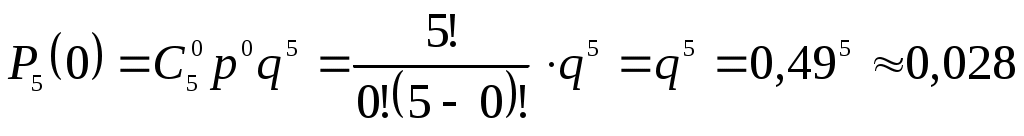 .
.
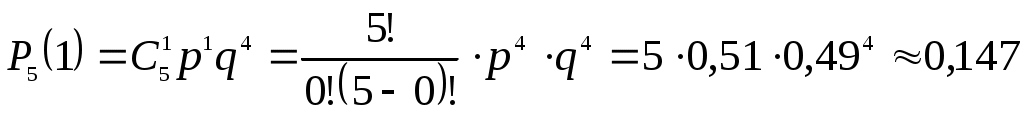
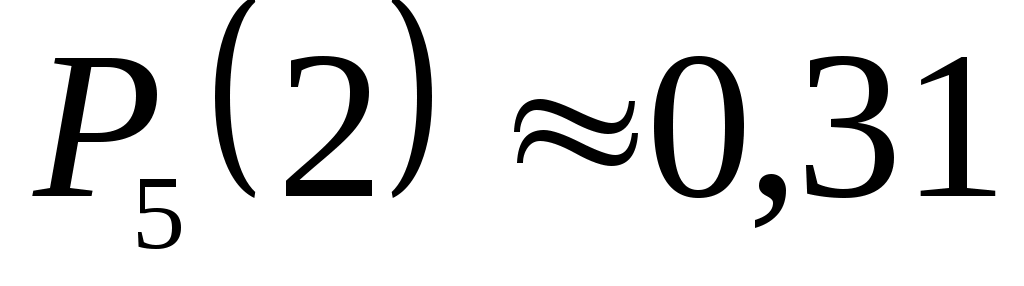 (см. а)).
(см. а)).
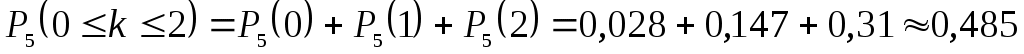
в) Событие {среди пяти детей более двух мальчиков} противоположно событию {среди пяти детей не более двух мальчиков}, поэтому его вероятность равна
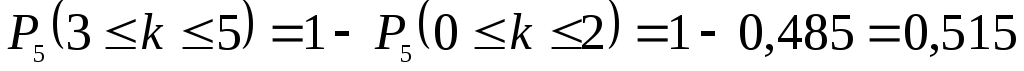 .
.
г) Вероятность того, что среди пяти детей не менее двух и не более трёх мальчиков, равна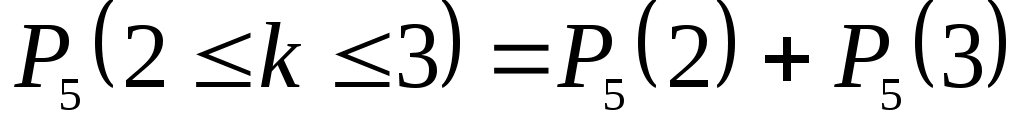 ,
, 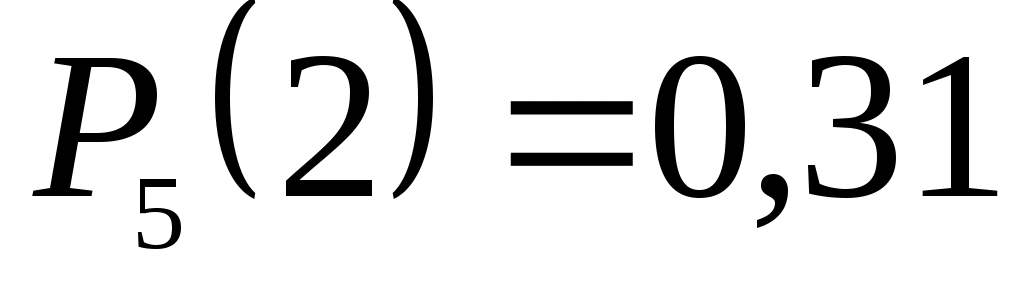 (см. а)).
(см. а)).
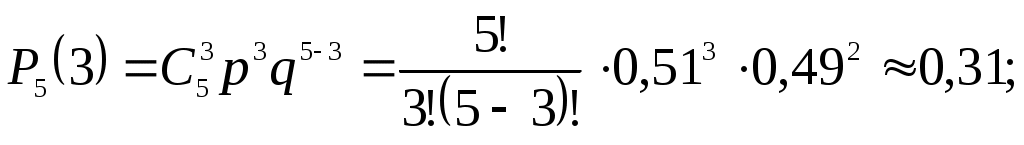
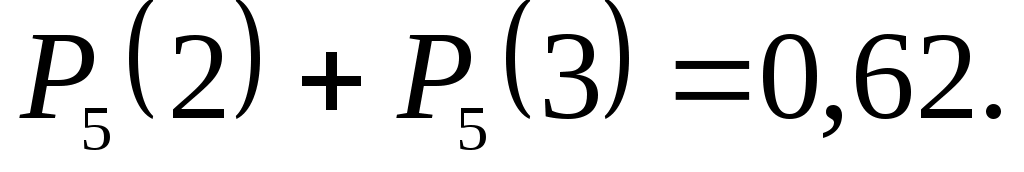
Пример 8. (Варианты 2, 9)
Сколько надо произвести независимых испытаний с вероятностью появления события в каждом испытании, равной 0,4, чтобы наивероятнейшее число появлений события в этих испытаниях было равно 25?
Решение:
По условию k0=25; р=0,4; q=0,6. Воспользуемся двойным неравенством np-q k0
k0 np+p. Подставляя данные задачи, получим систему неравенств для определения неизвестного числа n: 0,4n-0,6
np+p. Подставляя данные задачи, получим систему неравенств для определения неизвестного числа n: 0,4n-0,6  25, 0,4n+0,4
25, 0,4n+0,4 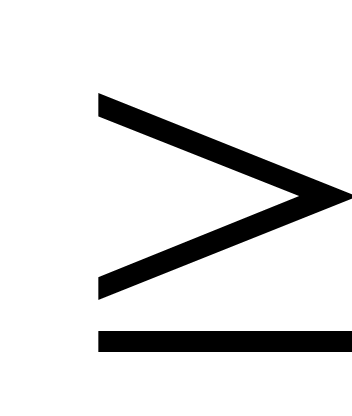 25. Из первого неравенства системы найдем n
25. Из первого неравенства системы найдем n 25,6/0,4=64. Из второго неравенства системы имеем n
25,6/0,4=64. Из второго неравенства системы имеем n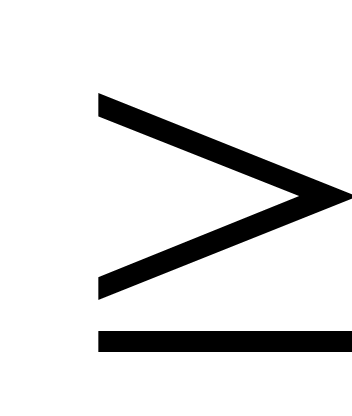 24,6/0,4=61,5. Итак, искомое число испытаний должно быть
24,6/0,4=61,5. Итак, искомое число испытаний должно быть 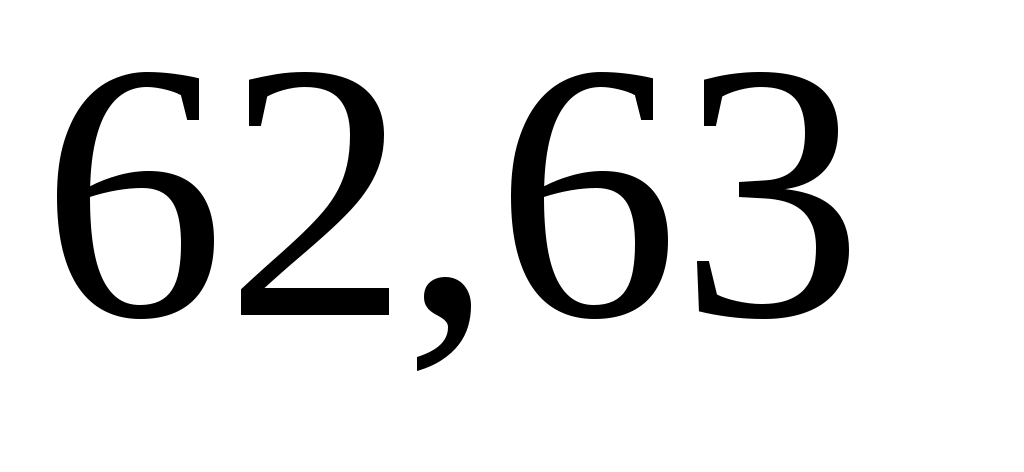 или 64.
или 64.
Пример 9. (Варианты 4, 6, 8, 10)
Вероятность появления события А в каждом из 2400 независимых испытаний постоянна и равна 0,6. Найти вероятность того, что событие А наступит: а) равно 1400 раз; б) от 1400 до 1800 раз; в) не менее 1400 раз.
Решение:
Число испытаний n=2400 велико; вероятность p=0,6 появления события A немала; q=1-p=0,4; npq=24000,60,4=14400,4 = 576 20, поэтому воспользуемся локальной и интегральной формулами Лапласа.
20, поэтому воспользуемся локальной и интегральной формулами Лапласа.
а) Имеем: n=2400, p=0,6, q=0,4, k=1400, np=1440, npq=576,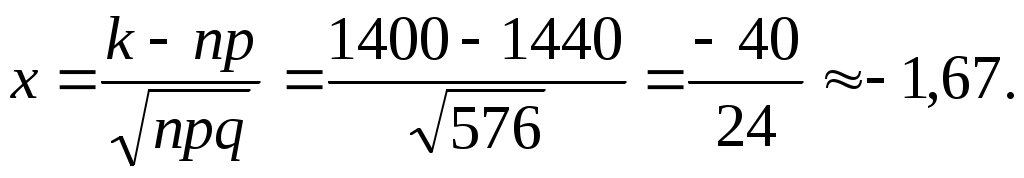
По формуле полной вероятности
Пример 6. (Варианты 1, 3, 5, 7, 9, 10)
Литьё в болванках поступает из двух заготовительных цехов: 70% из первого цеха, 30% из второго цеха. Литьё первого цеха имеет 10% брака, второго – 20% брака. Взятая наудачу болванка оказалась без дефекта. Какова вероятность её изготовления первым цехом?
Решение:
Событие А ={болванка без дефекта}.
Гипотеза H1 – болванка изготовлена первым цехом,
Гипотеза H2 – болванка изготовлена вторым цехом,
Литьё первого цеха имеет 10% брака, следовательно, 90% болванок, изготовленных первым цехом, не имеют дефекта и
По формуле Бейеса
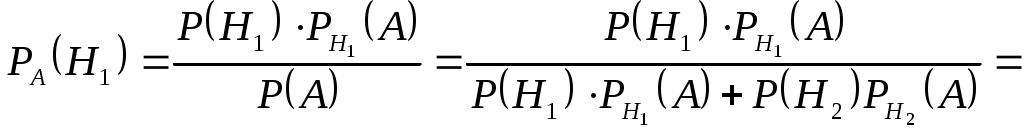
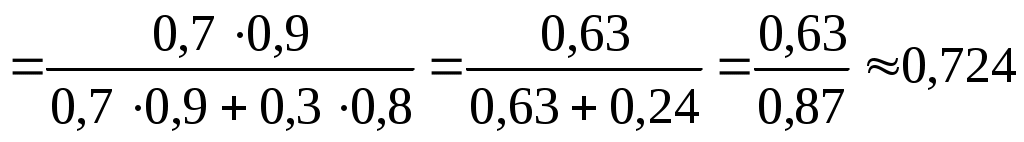 .
.Тема 4. Повторение независимых испытаний.
-
Формула Бернулли
Вероятность того, что в серии из п независимых испытаниях, в каждом из которых вероятность появления события A равна p (0р1), это событие наступит ровно k раз (безразлично в какой последовательности), равна
где
В различных задачах нас могут интересовать следующие вероятности:
– вероятность того, что в п испытаниях событие A наступит менее m раз
=
– вероятность того, что в п испытаниях событие A наступит более m раз
– вероятность того, что в п испытаниях событие A наступит не менее m раз
– вероятность того, что в п испытаниях событие A наступит не более m раз
– вероятность того, что в п испытаниях событие A наступит не менее
Все эти вероятности могут быть вычислены по формуле Бернулли, однако, на практике ввиду вычислительных сложностей это возможно лишь при небольших n и поэтому используются приближенные формулы.
-
Приближенные формулы Муавра- Лапласа
2.1. Локальная теорема Лапласа
Если число испытаний n велико, а вероятность p не очень мала, то
где
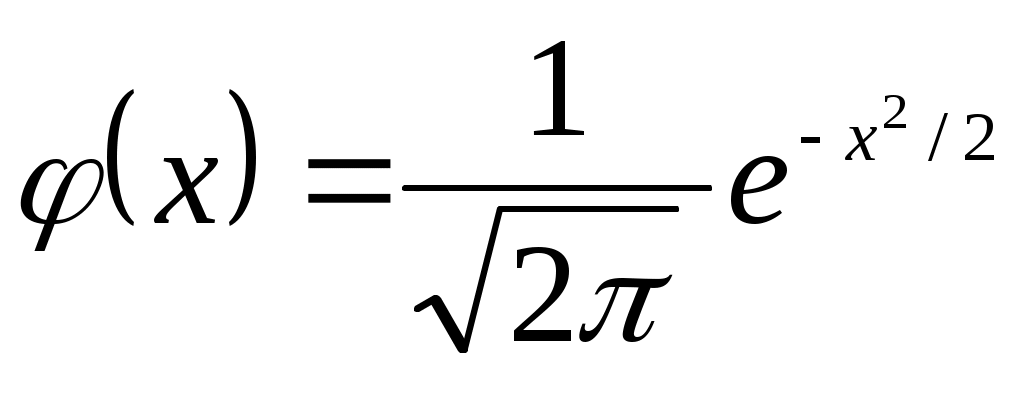 ,
, 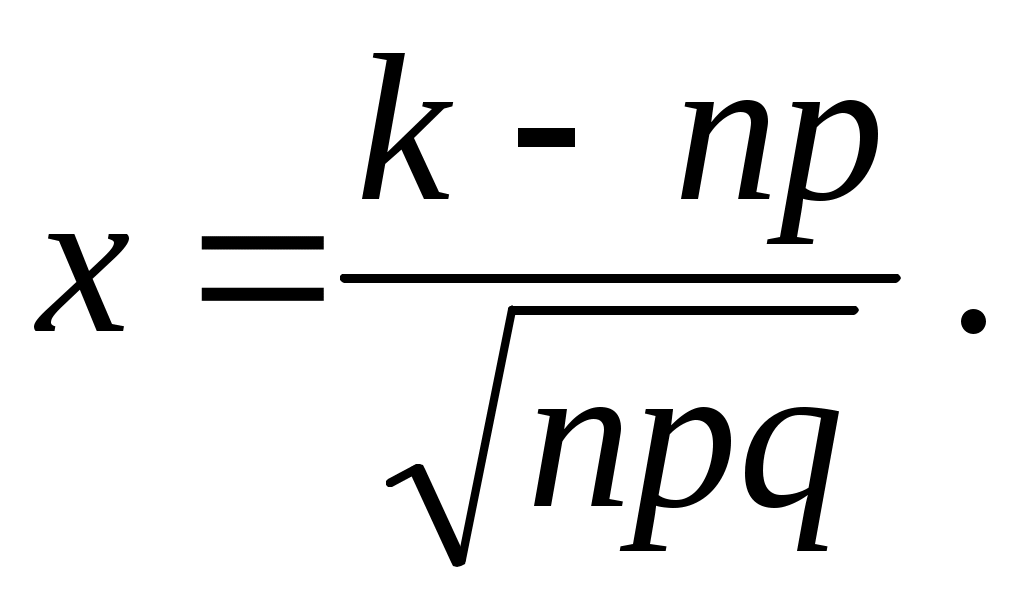
Значения функции
четная, и, следовательно,
2.2. Интегральная теорема Лапласа
Вероятность того, что событие А появится в n испытаниях не менее
где
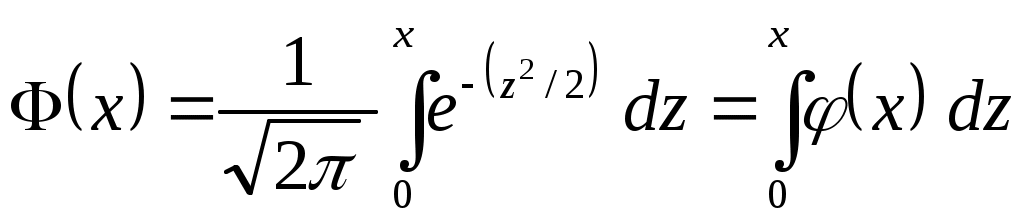 ,
, 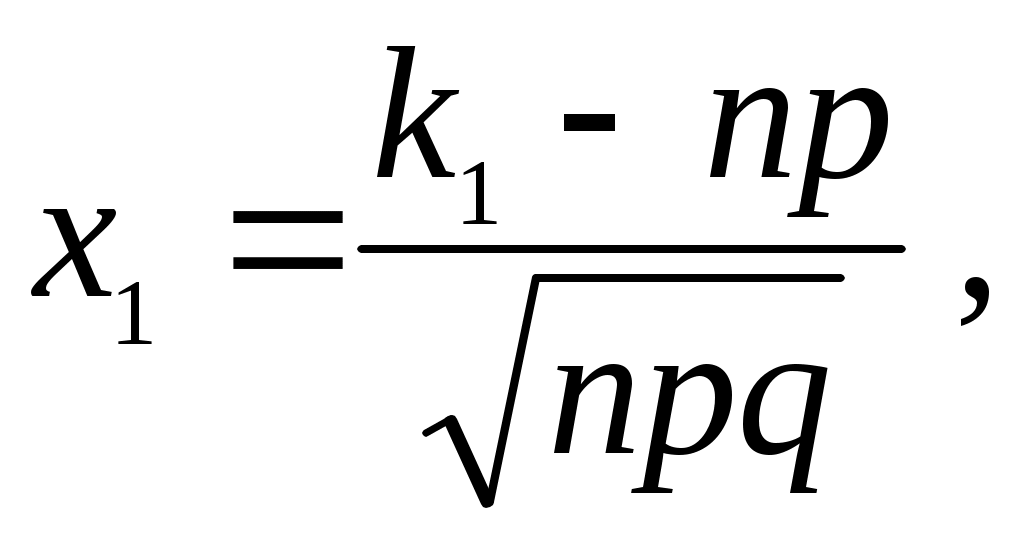
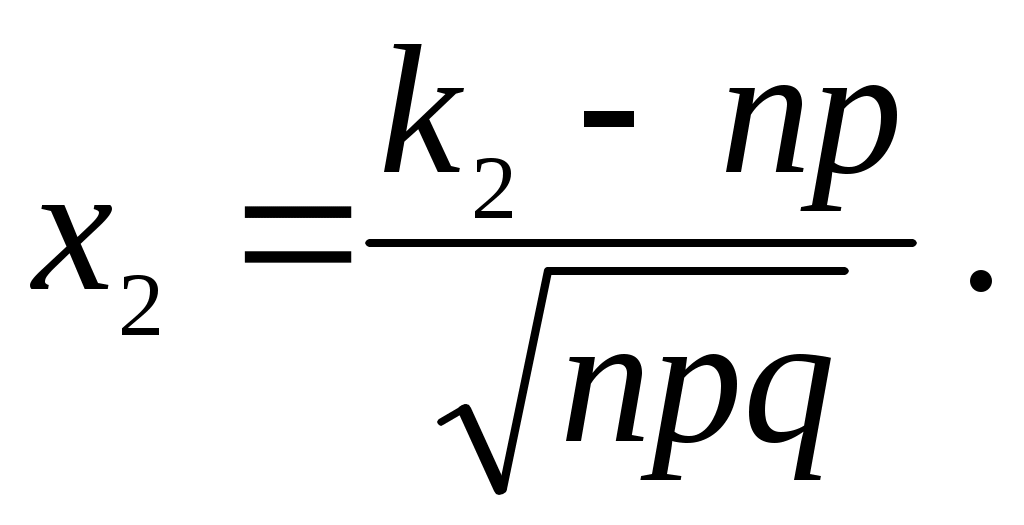
Значения функции Лапласа
-
Приближенная формула Пуассона
Если число испытаний n велико, а вероятность p появления события в каждом испытании очень мала, то
Обозначив , =np– среднее число успехов в серии испытаний, получим
Значение
4. Наивероятнейшее число успехов
Число k0 называется наивероятнейшим, если вероятность
Наивероятнейшее число k0 определяется из двойного неравенства
причем:
а) если число
б) если число
в) если
Пример 7. (Варианты 1, 7)
В семье пять детей. Найти вероятность того, что среди этих детей: а) ровно два мальчика; б) не более двух мальчиков; в) более двух мальчиков; г) не менее двух и не более трех мальчиков. Вероятность рождения мальчика принять равной 0,51.
Решение:
Число испытаний n=5 невелико, поэтому вероятности можно вычислить непосредственно по формуле Бернулли.
а) Вероятность того, что среди пяти детей ровно два мальчика, равна
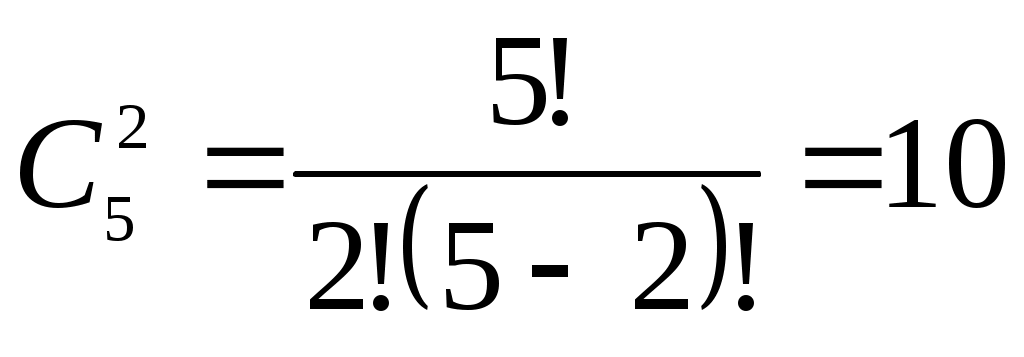 , p=0,51, q=1-p=0,49.
, p=0,51, q=1-p=0,49.б) Вероятность того, что среди пяти детей не более двух мальчиков, равна
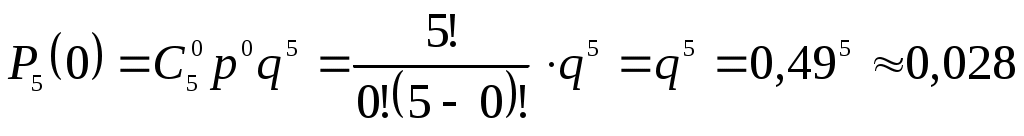 .
.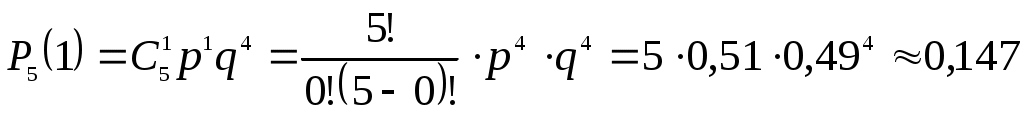
в) Событие {среди пяти детей более двух мальчиков} противоположно событию {среди пяти детей не более двух мальчиков}, поэтому его вероятность равна
г) Вероятность того, что среди пяти детей не менее двух и не более трёх мальчиков, равна
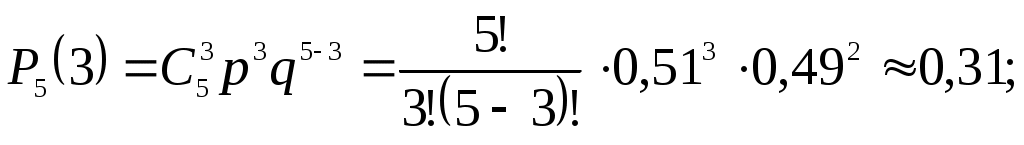
Пример 8. (Варианты 2, 9)
Сколько надо произвести независимых испытаний с вероятностью появления события в каждом испытании, равной 0,4, чтобы наивероятнейшее число появлений события в этих испытаниях было равно 25?
Решение:
По условию k0=25; р=0,4; q=0,6. Воспользуемся двойным неравенством np-q
Пример 9. (Варианты 4, 6, 8, 10)
Вероятность появления события А в каждом из 2400 независимых испытаний постоянна и равна 0,6. Найти вероятность того, что событие А наступит: а) равно 1400 раз; б) от 1400 до 1800 раз; в) не менее 1400 раз.
Решение:
Число испытаний n=2400 велико; вероятность p=0,6 появления события A немала; q=1-p=0,4; npq=24000,60,4=14400,4 = 576
а) Имеем: n=2400, p=0,6, q=0,4, k=1400, np=1440, npq=576,