ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 55
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Для того, чтобы роликовая цепь в процессе изнашивания не соскакивала с большей звездочки, необходимо выполнение условия z= 44
Тогда фактическое передаточное число
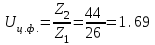
Отклонение
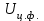 и
и 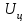 :
: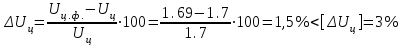 , что допустимо.
, что допустимо.3. Предварительное определение межосевого расстояния. По соображениям долговечности цепи предварительно величину межосевого расстояния будем принимать в диапазоне а = (30...50)рц, где рц - шаг цепи, мм.
4. Определение коэффициента эксплуатации кэ. По таблице 1П.29 приложения 1П [1,с. 391]:
а) коэффициент динамической нагрузки кД= 1,3 (нагрузка переменная);
б) коэффициент межосевого расстояния ка = 1 [для а = (30... 50)pц];
в) коэффициент наклона передачи к горизонту кн=1 (передача горизонтальная);
г
 ) коэффициент способа регулировки натяжения цепи кРЕГ = 1,25 (натяжение цепи не регулируется);
) коэффициент способа регулировки натяжения цепи кРЕГ = 1,25 (натяжение цепи не регулируется);д) коэффициент смазки и загрязнения передачи Kc - 1 [производство без пыли, качество смазки - II (удовлетворительная: густая внутришарнирная при V< 4 м/с, см. таблицу Ш. 28 приложения Ш) [1,с. 390];
е) коэффициент режима или продолжительности работы передачи в течении суток Креж=1 (работа в одну смену).
Тогда коэффициент эксплуатации
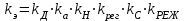 (2.2)
(2.2)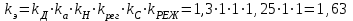
5. Определение коэффициентов kzи kn. Число зубьев малой звездочки типовой передачи принимается только
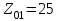 (см. таблицу 1П.30 приложения 1П) [1,с. 391]. Число зубьев малой звездочки проектируемой передачи Z1= 26. Тогда коэффициент числа зубьев:
(см. таблицу 1П.30 приложения 1П) [1,с. 391]. Число зубьев малой звездочки проектируемой передачи Z1= 26. Тогда коэффициент числа зубьев: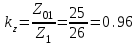
Частота вращения малой звездочки проектируемой передачи п3 = 95 об/мин. Ближайшая частота вращения малой звездочки типовой передачи п03 =100 об/мин (см. таблицу 1П.31 приложения 1П) [1,с. 391]. Тогда коэффициент частоты вращения:
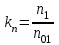 (2.3)
(2.3)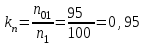
6.Выбор цепи.
Первоначально ориентируемся на однорядную цепь. Тогда расчетная мощность, передаваемая однорядной цепью для проектируемой передачи
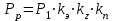 (2.4)
(2.4)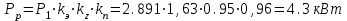

Ближайшей большей допускаемой расчетной мощностью [Рр] по табл. 1П.30 приложения 1П [1,с. 391] при Z01 = 26 и n01=95 об/мин является [РР] = 11 кВт для однорядной цепи ПР-25.4 - 57600 с шагом рц = 25.4 мм.
Для того, чтобы решить вопрос о том, подходит нам однорядная цепь с таким шагом или нет, определим, какие же при этом получаются делительные диаметры звездочек:
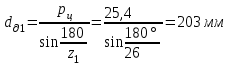
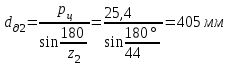
Скорость цепи:
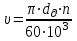 (2.5)
(2.5)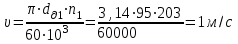
По табл. 1П. 28 приложения 1П [1,с. 390] при
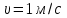 назначаем для цепи густую внутришарнирную смазку (качество смазки II).
назначаем для цепи густую внутришарнирную смазку (качество смазки II).7
 . Определение межосевого расстояния и длины цепи. Ранее (см. п. 3) из соображений долговечности цепи мы приняли, что предварительная величина межосевого расстояния а будет находится в диапазоне
. Определение межосевого расстояния и длины цепи. Ранее (см. п. 3) из соображений долговечности цепи мы приняли, что предварительная величина межосевого расстояния а будет находится в диапазонеа = (30...50) рц.
Так как меньшее значение рекомендуется [3] для Uц = 1 ...3, а большее для Uц = 6...7, при иц = 1,7 принимаем, а = 35
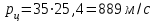 .
. Длина цепи в шагах или число звеньев цепи
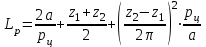 (2.6)
(2.6)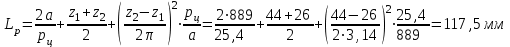
Округляем LPдо целого четного числа, для того, чтобы не применять специальных соединительных звеньев. Для принятого значения LP= 118 уточняем а:
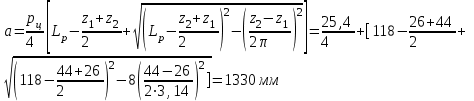
Так как цепная передача работает лучше при небольшом провисании холостой ветви цепи, расчетное межосевое расстояние, а уменьшают на величину
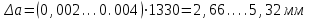 . Тогда принимаем
. Тогда принимаем 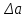 =4 мм и тогда окончательная величина межосевого расстояния
=4 мм и тогда окончательная величина межосевого расстояния 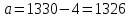 мм.
мм.8. Силы в цепной передаче и требования монтажа.
Окружная сила:
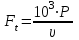 (2.7)
(2.7)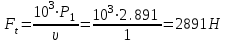
По табл. 1П.33 приложения 1П [1,с. 393] коэффициент провисания цепи при горизонтальном ее расположении kf=6.
П
 о табл. 1П. 31 приложения 1П масса 1 м цепи ПР [1,с. 391] с шагом рц= 25.4 мм составляет 2.6 кг, т.е. погонная масса q=2.6 кг/м.
о табл. 1П. 31 приложения 1П масса 1 м цепи ПР [1,с. 391] с шагом рц= 25.4 мм составляет 2.6 кг, т.е. погонная масса q=2.6 кг/м.Натяжение цепи от силы тяжести провисающей ведомой ветви
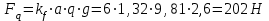 , где а = 1,32 м; g= 9,81м/с2 - ускорение свободного падения.
, где а = 1,32 м; g= 9,81м/с2 - ускорение свободного падения.Натяжение цепи от центробежных сил
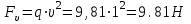
Разрушающая нагрузка цепи ПР с шагом рч= 25.4 мм по табл. 1П.31 [1,с. 391] FP = 25.4 кН= 57600 Н. Уточним расчетный коэффициент запаса прочности цепи
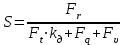 (2.8)
(2.8)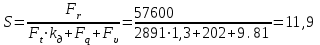
где
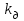 =1,3 -коэффициент динамической нагрузки (см. п.4).
=1,3 -коэффициент динамической нагрузки (см. п.4).Допускаемый коэффициент запаса прочности цени но табл. 1П.34 приложения 1П [1,с. 393] линейным интерполированием [S] = 8.3.
Цепь ПР – 25.4 - 57600 подходит, так как S=11.9>[S] = 8.3.
Нагрузка на валы цепной передачи:
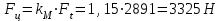
где км= 1,15 - при горизонтальной передаче и угле наклона передачи < 40°; км = 1,05 - при угле наклона передачи более 40° и при вертикальной передаче. Сила Fц направлена по линии, соединяющей центры звездочек.
При монтаже цепной передачи предельное отклонение AS(мм) звездочек от од ной плоскости и предельные углы их смещения S, перекоса валов у и их скрещивания (град) (рис. 3.2) определяют по формуле:
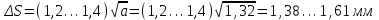 ;
;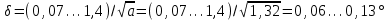
 ;
;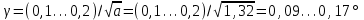 ;
;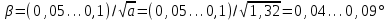 .
.3. Расчет редукторных передач
3.1 Расчет первой ступени

Исходные данные для расчета:
а) частота вращения шестерни n2=950 об/мин;
б) частота вращения колеса n3= 266 об/мин;
в) передаточное число ступени Uб = 3,57;
г) вращающий момент на валу колеса Т3 =135 Н • м.
д) расчетный срок службы (ресурс работы) Lh=10000 ч;
Проектный расчет
1.Выбор варианта термообработки зубчатых колес.
Принимаем вариант термообработки (т.о.) I (см. табл. 1П.6 приложения 1П): т.о. шестерни - улучшение, твердость поверхности 269...302 НВ; т.о. колеса - улучшение, твердость поверхности 235...262 НВ; марки сталей одинаковы для шестерни и колеса: 40Х;
2.Предварительное определение допускаемого контактного напряжения при проектном расчете на сопротивление контактной усталости. Средняя твердость H поверхности зубьев:
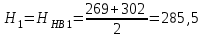 НВ;
НВ; 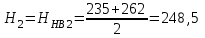 НВ;
НВ;Предел контактной выносливости поверхности зубьев σH lim, соответствующий базовому числу циклов напряжений (см. табл. 1П.9 приложения 1П) для т.о. улучшение:
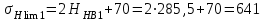 МПа;
МПа;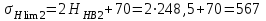 МПа;
МПа;Расчетный коэффициент SН (табл. 1П.9 приложения 1П) для т.о. улучшение :
SН1= SН2=1,1.
Базовое число циклов напряжений NН lim:
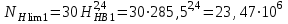 ;
;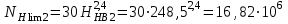 ;
;Эквивалентное число циклов напряжений NНE за расчетный срок службы передачи Lh=10000 часов:
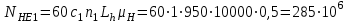 ;
;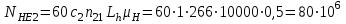 ;
;где с1, и с2 -число зацеплений за один оборот соответственно зуба шестерни и зуба колеса; с1=1; с2 = 1;
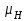 =0,5.
=0,5.Определяем коэффициенты долговечности ZN1 и ZN2. Так как NНE1 > NНlim1, тогда
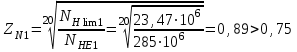
 .
.Так как NНE2 > NНlim2, тогда
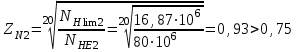 .
.Предварительная величина допускаемого контактного напряжения при расчете передачи на сопротивление контактной усталости:
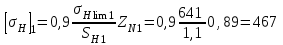 МПа;
МПа;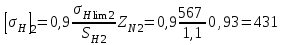 МПа;
МПа;В качестве расчетного допускаемого контактного напряжения [σн] при расчете прямозубой цилиндрической передачи на контактную усталость принимается минимальное напряжение из [σн]1 и [σн]2.
В нашем примере [σн]= [σн]1=431МПа.
3
 . Определение межосевого расстоянии. По табл. 1П.11 приложения 1П выберем коэффициент ψba. В данной таблице в зависимости от расположения зубчатых колес относительно опор и твердости рабочих поверхностей зубьев указывается диапазон рекомендуемых значений ψba. В указанном диапазоне ψba рекомендуется принимать из ряда стандартных чисел: 0,15; 0,2; 0,25; 0,315; 0,4 и 0,5. Данных рекомендаций допускается не придерживаться при проектировании нестандартных редукторов.
. Определение межосевого расстоянии. По табл. 1П.11 приложения 1П выберем коэффициент ψba. В данной таблице в зависимости от расположения зубчатых колес относительно опор и твердости рабочих поверхностей зубьев указывается диапазон рекомендуемых значений ψba. В указанном диапазоне ψba рекомендуется принимать из ряда стандартных чисел: 0,15; 0,2; 0,25; 0,315; 0,4 и 0,5. Данных рекомендаций допускается не придерживаться при проектировании нестандартных редукторов.В нашем примере шестерня рассчитываемой ступени расположена симметрично относительно опор, а колесо - симметрично (см. схему привода). По табл. 1П.11 приложения 1П при HB1<350 и HB2<350 принимаем из диапазона ψba = 0,3...0,5 расчетное значение ψba =0,4 и значение ψbdmax=1,4.
Тогда коэффициент ψba (предварительно):
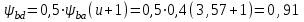
По табл. 1П.12 приложения 1П при НВ1<350 и НВ2 <350 для кривой V (редуктор соосный) принимаем коэффициент КHβ = 1,01.
Приняв для прямозубой цилиндрической передачи вспомогательный коэффициент Кα= 495, определим предварительно межосевое расстояние а'w :
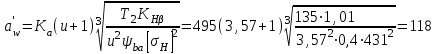 мм.
мм.По табл. 1П. 13 приложения 1П принимаем ближайшее стандартное значение аw = 120мм.
4. Определение модуля передачи.
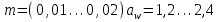 мм
ммПо табл. 1П.14 приложения 1П для полученного диапазона модулей пользуемся стандартными значениями 1-го ряда, примем m =2 мм.
5. Определение чисел зубьев шестерни и колеса. Суммарное число зубьев
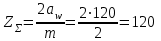
Число зубьев шестерни
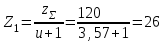

Принимаем Z1=25.
Число зубьев колеса
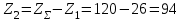 .
.6. Определение фактического передаточного числа ступени.
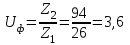
Отклонение Uф от U:
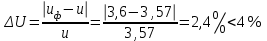 .
.7. Определение основных размеров шестерни и колеса. Диаметры делительные:
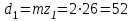 мм;
мм;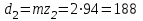 мм.
мм.Проверка:
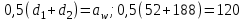 мм
ммПримем коэффициент высоты головки зуба ha* = 1 и коэффициент радиального зазора с*= 0,25. Тогда, диаметры окружностей вершин da и впадин df зубьев при высотной модификации:
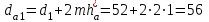 мм;
мм; 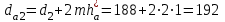 мм;
мм;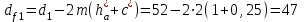 мм;
мм;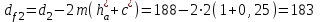 мм.
мм.Ширина венца колеса
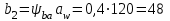 мм.
мм. Ширина венца шестерни
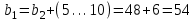 мм.
мм. П
 роверочный расчет
роверочный расчет8. Проверка пригодности заготовок зубчатых колес и выбор материала
для их изготовления. Диаметр заготовки шестерни
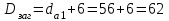 мм.
мм.Условие пригодности заготовки шестерни
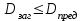 ,
,Где Dпред -см. табл.1П.7 приложения 1П. Для стали 40Х при т.о. улучшение для твердости поверхности 235...262 НВ Dпред=200 мм. Таким образом, для изготовления шестерни принимаем сталь 40Х. Выберем материал для изготовления колеса. Для этого определим толщину заготовки диска колеса Сзаг и толщину заготовки обода Sзаг:
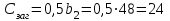 мм;
мм;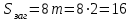 мм.
мм.Наибольшую из величин Сзаг и Sзаг сравниваем для той же марки стали, что и для шестерни (т.е. 40Х) по табл. 1П.7 приложения 1П при т.о. улучшение для твердости поверхности 235...262 НВ с Sпред =125 мм. Условие Сзаг =24< Sпред =125 мм выполняется. Таким образом, для изготовления колеса также подходит сталь 40Х
9. Определение степени точности передачи. Окружная скорость υ (м/с)
шестерни или колеса в полюсе зацепления одинакова и может быть определена:
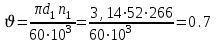 м/с.
м/с.По табл. 1П.15 приложения 1П, исходя из υ =0,7 м/с для прямозубых цилиндрических передач выбираем 9-ю степень точности, при которой допускается окружная скорость зубчатых колес до 4 м/с.
10. Уточнение допускаемого контактного напряжения при проверочном расчете на сопротивление контактной усталости. На основании рекомендаций, изложенных в п. 2.1, принимаем параметр шероховатости Rа = 3,2 мкм и коэффициент ZR =0,9. Коэффициент ZV =1, т.к. υ<5 м/с.
Т
 огда по формуле:
огда по формуле: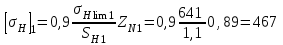 МПа;
МПа;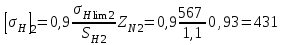 МПа;
МПа;Таким образом, уточненные величины [σн]1 и [σн]2 остались такими же , как и при предварительном расчете ввиду того, что произведение ZR ZV оказалось равным 0,9.
С
 ледовательно, уточненная величина расчетного допускаемого контактного напряжения [σн] будет такой же, как и при предварительном расчете, т.е. [σн]=431МПа (см. п. 2).
ледовательно, уточненная величина расчетного допускаемого контактного напряжения [σн] будет такой же, как и при предварительном расчете, т.е. [σн]=431МПа (см. п. 2).11. Определение сил, действующих в прямозубом зацеплении. Окружная сила Ft на делительном цилиндре
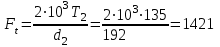 Н
Н При этом для шестерни и колеса:
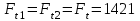 Н.
Н. Радиальная сила Fr:
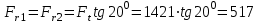 Н.
Н.12.Определение коэффициента нагрузки Кн. При расчете на сопротивление контактной усталости
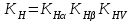
Коэффициент КНа = 1 -для прямозубых передач.
Коэффициент KHβ уточняем по той же кривой V при HB1<350 и HB2<350 (см. табл. 1П.12 приложения 1П), что и при предварительном расчете в п.3, в зависимости от уточненной в п.7 величины ψbd=0,98. При этом коэффициент Kнβ практически не изменился: KHβ=1,01.
По табл. 1П.17 приложения 1П коэффициент δН=0,06 при HB1<350 и HB2<350 .
По табл. 1П.18 приложения 1П коэффициент g0= 7,3 (при m=2 мм и 9-й степени точности).
Тогда динамическая добавка
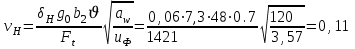
Коэффициент KHV:
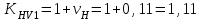 .
.Окончательно
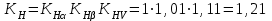
 .
.13. Проверочный расчет передачи на сопротивление контактной усталости. Для стальных зубчатых колес коэффициент ZH, учитывающий механические свойства материалов сопряженных зубьев: ZЕ =190 МПа1/2.
Коэффициент ZН, учитывающий форму сопряженных поверхностей зубьев, для прямозубых передач без смещения.
Коэффициент торцового перекрытия зубьев для прямозубой передачи приближенно можно определить по формуле
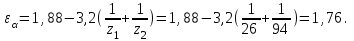
Коэффициент, учитывающий суммарную длину контактных линий, для прямозубой передачи
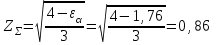 .
.Расчетное значение контактного напряжения
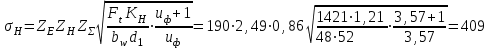 МПа
МПаСопротивление контактной усталости обеспечивается, так как выполняется условие: σн=409 МПа < [σн]=431 МПа.
14. Определение допускаемого напряжения изгиба при расчете зубьев на сопротивление усталости при изгибе. По табл. 1П.9 приложения 1П принимаем:
а) для шестерни (т. о. улучшение + закалка ТВЧ), при m<3 мм.
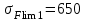 МПа;
МПа; 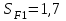 ;
;б) для колеса (т. о. улучшение)
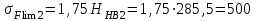 МПа, (см. п.2),
МПа, (см. п.2), 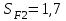
Эквивалентное число циклов напряжений NFE за расчетный срок службы Lh =10*103 часов:
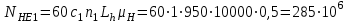 ;
;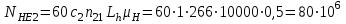 ;
;где с, и с2 - см. п. 2.
На основании рекомендаций, изложенных в п. 2.1, определяем коэффициенты долговечности YN1 и YN2.
Для шестерни при NFE> NFlim1 принимается YN1 =1.
Для колеса при при NFE> NFlim1 принимается YN1 =1.
Тогда допускаемое напряжение изгиба:
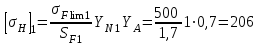
 МПа;
МПа;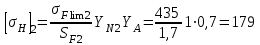 МПа.
МПа.1
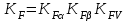 5. Определение коэффициента нагрузки КF. Коэффициент нагрузки при расчете зубьев на сопротивление усталости при изгибе:
5. Определение коэффициента нагрузки КF. Коэффициент нагрузки при расчете зубьев на сопротивление усталости при изгибе:Коэффициент КFа = 1 -для прямозубых передач.
Коэффициент KFβ принимаем по табл. 1П.12 приложения 1П при HB1<350 и HB2<350 при ψbd=0,98 (кривая V): KFβ =1,1.
Коэффициент δF ,учитывающий влияние вида зубчатой передачи и модификации профиля зубьев: δF =0,16 .
Коэффициент g0= 7,3- см. п.12.
Тогда динамическая добавка
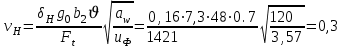
Коэффициент KHV:
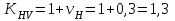 .
.Окончательно
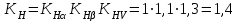 .
.16 Проверочный расчет зубьев на сопротивление усталости при изгибе.
Коэффициент YFS, учитывающий форму зуба и концентрацию напряжений:
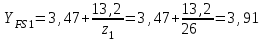
 ;
;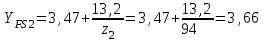 .
.Тогда расчетное напряжение изгиба σF:
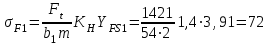 МПа;
МПа;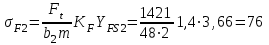 МПа.
МПа.Сопротивление усталости при изгибе обеспечивается, так как выполняются условия:
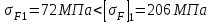
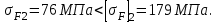
Отмечаем, что для данного варианта термообработки основным критерием работоспособности передачи является сопротивление контактной усталости, а не усталости при изгибе.
17. Проверочный расчет передачи на контактную прочность при действии пиковой нагрузки (при кратковременной перегрузке). Цель данного расчета - проверка статической прочности зубьев при действии пиковой нагрузки (при кратковременной перегрузке), не учтенной при расчете на сопротивление контактной усталости. По табл. 1П.9 приложения 1П предельно допускаемое контактное напряжение
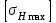 :
: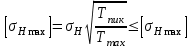 МПа;
МПа;где -
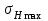 - максимальное контактное напряжение,
- максимальное контактное напряжение, 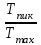 - кратковременная перегрузка.
- кратковременная перегрузка. Определяем для шестерни и колеса
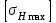 согласно таблице 1П.9 приложения 1П.:
согласно таблице 1П.9 приложения 1П.:а) для шестерни:
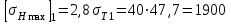 МПа.
МПа.б) для колеса
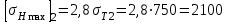 МПа.
МПа.В качестве расчётной принимаем наименьшую величину
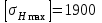 МПа.
МПа.Тогда для рассчитываемой ступени:
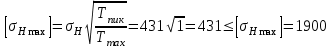 МПа.
МПа.18. Проверочный расчет передачи при изгибе пиковой нагрузкой (при кратковременной перегрузке). Цель данного расчета - проверка статической прочности зубьев при действии пиковой нагрузки (при кратковременной перегрузке), не учтенной при расчете зубьев на сопротивление усталости при изгибе.
По табл. 1П.9 приложения 1П предельно допускаемое напряжение изгиба
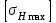 :
: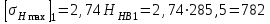 Мпа;
Мпа;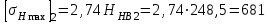 Мпа,
Мпа,Максимальное напряжение изгиба σFmax при кратковременной перегрузке:
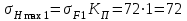 МПа,
МПа,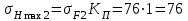 МПа,
МПа,где σF1 =72 МПа и σF1 =76 МПа - см. п. 16.
С
 татическая поломка зубьев при кратковременной перегрузке будет отсутствовать, так как выполняются условия:
татическая поломка зубьев при кратковременной перегрузке будет отсутствовать, так как выполняются условия: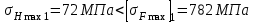
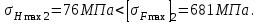
350>350>3>350>350>350>350>5>350>350>350>350>
1 2 3
3
 .2 Расчет второй ступени
.2 Расчет второй ступениИсходные данные для расчета:
а) частота вращения шестерни n3=266 об/мин;
б) частота вращения колеса n4= 95 об/мин;
в) передаточное число ступени Uт= 2,8;
г) вращающий момент на валу колеса Т4 =363 Н • м.
д) расчетный срок службы (ресурс работы) Lh=10000 ч;
Проектный расчет
1.Выбор варианта термообработки зубчатых колес.
Принимаем вариант термообработки (т.о.) I (см. табл. 1П.6 приложения 1П): т.о. шестерни - улучшение, твердость поверхности 269...302 НВ; т.о. колеса - улучшение, твердость поверхности 235...262 НВ; марки сталей одинаковы для шестерни и колеса: 40Х;
2.Предварительное определение допускаемого контактного напряжения при проектном расчете на сопротивление контактной усталости. Средняя твердость H поверхности зубьев:
 НВ;
НВ;  НВ;
НВ;Предел контактной выносливости поверхности зубьев σH lim, соответствующий базовому числу циклов напряжений (см. табл. 1П.9 приложения 1П) для т.о. улучшение:
 МПа;
МПа; МПа;
МПа;Расчетный коэффициент SН (табл. 1П.9 приложения 1П) для т.о. улучшение :
SН1= SН2=1,1.
Базовое число циклов напряжений NН lim:
 ;
; ;
;Эквивалентное число циклов напряжений NНE за расчетный срок службы передачи Lh=10000 часов:
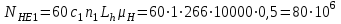 ;
;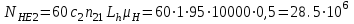 ;
;где с1, и с2 -число зацеплений за один оборот соответственно зуба шестерни и зуба колеса; с1=1; с2 = 1;
 =0,5.
=0,5.Определяем коэффициенты долговечности ZN1 и ZN2. Так как NНE1 > NНlim1, тогда
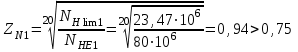
 .
.Так как NНE2 > N
Нlim2, тогда
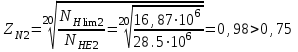 .
.Предварительная величина допускаемого контактного напряжения при расчете передачи на сопротивление контактной усталости:
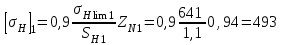 МПа;
МПа;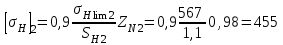 МПа;
МПа;В качестве расчетного допускаемого контактного напряжения [σн] при расчете прямозубой цилиндрической передачи на контактную усталость принимается минимальное напряжение из [σн]1 и [σн]2.
В нашем примере [σн]= [σн]1=455МПа.
3
 . Определение межосевого расстоянии. По табл. 1П.11 приложения 1П выберем коэффициент ψba. В данной таблице в зависимости от расположения зубчатых колес относительно опор и твердости рабочих поверхностей зубьев указывается диапазон рекомендуемых значений ψba. В указанном диапазоне ψba рекомендуется принимать из ряда стандартных чисел: 0,15; 0,2; 0,25; 0,315; 0,4 и 0,5. Данных рекомендаций допускается не придерживаться при проектировании нестандартных редукторов.
. Определение межосевого расстоянии. По табл. 1П.11 приложения 1П выберем коэффициент ψba. В данной таблице в зависимости от расположения зубчатых колес относительно опор и твердости рабочих поверхностей зубьев указывается диапазон рекомендуемых значений ψba. В указанном диапазоне ψba рекомендуется принимать из ряда стандартных чисел: 0,15; 0,2; 0,25; 0,315; 0,4 и 0,5. Данных рекомендаций допускается не придерживаться при проектировании нестандартных редукторов.В нашем примере шестерня рассчитываемой ступени расположена симметрично относительно опор, а колесо - симметрично (см. схему привода). По табл. 1П.11 приложения 1П при HB1<350 и HB2<350 принимаем из диапазона ψba = 0,3...0,5 расчетное значение ψba =0,3 и значение ψbdmax=1,4.
Тогда коэффициент ψba (предварительно):
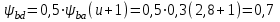
По табл. 1П.12 приложения 1П при НВ1<350 и НВ2 <350 для кривой V (редуктор соосный) принимаем коэффициент КHβ = 1,1.
Приняв для прямозубой цилиндрической передачи вспомогательный коэффициент Кα= 495, определим предварительно межосевое расстояние а'w :
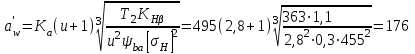 мм.
мм.По табл. 1П. 13 приложения 1П принимаем ближайшее стандартное значение аw = 180мм.
4. Определение модуля передачи.
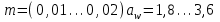 мм
ммПо табл. 1П.14 приложения 1П для полученного диапазона модулей пользуемся стандартными значениями 1-го ряда, примем m =2 мм.
5. Определение чисел зубьев шестерни и колеса. Суммарное число зубьев
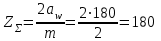
Число зубьев шестерни
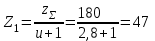

Принимаем Z1=47.
Число зубьев колеса
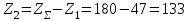 .
.6. Определение фактического передаточного числа ступени.
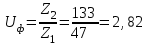
Отклонение Uф от U:
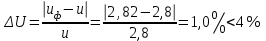 .
.7. Определение основных размеров шестерни и колеса. Диаметры делительные:
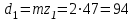 мм;
мм;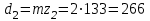 мм.
мм.Проверка:
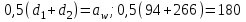 мм
ммПримем коэффициент высоты головки зуба ha* = 1 и коэффициент радиального зазора с*= 0,25. Тогда, диаметры окружностей вершин da и впадин df зубьев при высотной модификации:
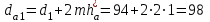 мм;
мм; 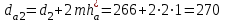 мм;
мм;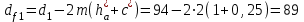 мм;
мм;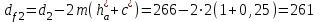 мм.
мм.Ширина венца колеса
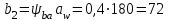 мм.
мм. Ширина венца шестерни
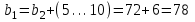 мм.
мм. Уточняем коэффициент ψbd:
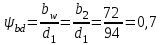
П
 роверочный расчет
роверочный расчет8. Проверка пригодности заготовок зубчатых колес и выбор материала
для их изготовления. Диаметр заготовки шестерни
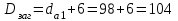 мм.
мм.Условие пригодности заготовки шестерни
 ,
,Где Dпред -см. табл.1П.7 приложения 1П. Для стали 40Х при т.о. улучшение для твердости поверхности 235...262 НВ Dпред=200 мм. Таким образом, для изготовления шестерни принимаем сталь 40Х. Выберем материал для изготовления колеса. Для этого определим толщину заготовки диска колеса Сзаг и толщину заготовки обода Sзаг:
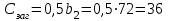 мм;
мм;
мм.
Наибольшую из величин Сзаг и Sзаг сравниваем для той же марки стали, что и для шестерни (т.е. 40Х) по табл. 1П.7 приложения 1П при т.о. улучшение для твердости поверхности 235...262 НВ с Sпред =125 мм. Условие Сзаг =36< Sпред =125 мм выполняется. Таким образом, для изготовления колеса также подходит сталь 40Х
9. Определение степени точности передачи. Окружная скорость υ (м/с)
шестерни или колеса в полюсе зацепления одинакова и может быть определена:
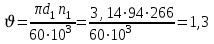 м/с.
м/с.По табл. 1П.15 приложения 1П, исходя из υ =1.3 м/с для прямозубых цилиндрических передач выбираем 9-ю степень точности, при которой допускается окружная скорость зубчатых колес до 4 м/с.
10. Уточнение допускаемого контактного напряжения при проверочном расчете на сопротивление контактной усталости. На основании рекомендаций, изложенных в п. 2.1, принимаем параметр шероховатости Rа = 3,2 мкм и коэффициент ZR =0,9. Коэффициент ZV =1, т.к. υ<5 м/с.
Т
 огда по формуле:
огда по формуле: МПа;
МПа;
 МПа;
МПа;Таким образом, уточненные величины [σн]1 и [σн]2 остались такими же , как и при предварительном расчете ввиду того, что произведение ZR ZV оказалось равным 0,9.
Следовательно, уточненная величина расчетного допускаемого контактного напряжения [σн] будет такой же, как и при предварительном расчете, т.е. [σн]=455 МПа (см. п. 2).
11. Определение сил, действующих в прямозубом зацеплении. Окружная сила Ft на делительном цилиндре
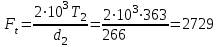 Н
Н При этом для шестерни и колеса:
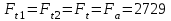 Н.
Н. Радиальная сила Fr:
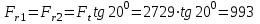 Н.
Н.12.Определение коэффициента нагрузки Кн. При расчете на сопротивление контактной усталости

Коэффициент КНа = 1 -для прямозубых передач.
Коэффициент KHβ уточняем по той же кривой V при HB