ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 109
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
динамике) и/или несколько показателей, то необходимо применение статистических методов много- мерного анализа. Их описание выходит за рамки настоящей работы, ознакомиться с ними можно в пуб- ликациях, перечисленных в упомянутой во введении работе автора.
Рассмотрим методы решения типовых для педагогических исследований задач анализа данных.
Алгоритм выбора статистического критерия. Поясним, как следует выбирать статистические критерии, то есть приведем алгоритм выбора статистического критерия – процедуру принятия решения относительно того, какой статистический критерий использовать в той или иной ситуации.
В первом приближении этот алгоритм чрезвычайно прост: если данные получены в результате измерений в шкале отношений, то следует использовать критерий Вилкоксона-Манна-Уитни (ВМУ), если в порядковой шкале, то критерий c 2.
Возможные модификации этого правила принятия решений (учитывающие большее число факто- ров) приведены на рисунке 1.
Во-первых, необходимо определить какая шкала измерений используется – отношений или поряд- ковая.
Для шкалы отношений следует решить, состоит ли решаемая задача в обнаружении различия сред- них значений (математических ожиданий). Если – да, то можно использовать критерий Крамера-Уэлча (описание методик применения всех упоминаемых статистических критериев приведено ниже). Если же следует обнаружить произвольные различия характеристик выборок, то следует использовать критерий Вилкоксона-Манна-Уитни или критерий 2.
Если число различающихся между собой значений10 в сравниваемых выборках велико (более деся- ти), то целесообразно использование критерия Вилкоксона-Манна-Уитни.
9Встречаютсяслучаи,когдаимеетсянесколькоэкспериментальныхилинесколькоконтрольныхгрупп.Приэтомпопарноеих сравнениевсеравноявляетсяодной из базовыхзадач.
10Например,выборка(1,2,2,2, 1, 1, 2,1, 1, 1) содержитвсегодваразличныхзначения–единицуидвойку.Втожевремя,
например,выборка (2,0,1,5,8,4,2,7,3,9) того жеобъема(десять элементов) содержитдесять различныхзначений.
Если число различающихся между собой значений в сравниваемых выборках мало (менее десяти), то, произведя группировку результатов измерений (то есть, перейдя от шкалы отношений к порядковой шкале – см. выше пятый раздел), можно использовать критерий 2.
Далее, аналогично рассуждая, если объем выборок мал11 (N, M 50), то следует использовать кри- терий Вилкоксона-Манна-Уитни (при малом числе различающихся значений в этом случае можно ис- пользовать и критерий 2).
Если объем выборок велик, то, опять же с помощью группировки результатов измерений, имеет смысл использовать критерий 2.
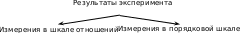
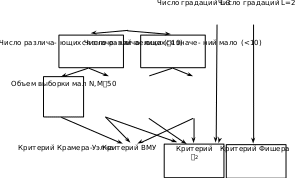Рис.1.Алгоритмвыборастатистическогокритерия
Для порядковой шкалы в случае, когда число градаций (различных баллов) больше либо равно трем, используется критерий 2, если же применялась дихотомическая шкала, то можно использовать либо критерий 2, либо критерий Фишера.
Использование компьютера при анализе результатов педагогических экспериментов, несомненно, целесообразно. Однако использовать статистические критерии, "зашитые" в пакеты программ следует осторожно. Все четыре предлагаемых к использованию для обработки результатов педагогического эксперимента статистических критерия (Крамера-Уэлча, Вилкоксона-Манна-Уитни, 2 и Фишера) кор- ректно реализованы в профессиональных статистических пакетах, среди которых можно выделить и рекомендовать такие наиболее распространенные пакеты статистического анализа как: Statistica, StatGraphics и SPSS. Однако, упомянутые программы, во-первых, являются лицензионными и стоят достаточно дорого. Во-вторых, они достаточно сложны и требуют значительных временных затрат для своего освоения. Наряду с этим, существуют инструменты статистического анализа в электронных таблицах Microsoft Excel, входящих в стандартный комплект Microsoft Office и установленных, навер- ное, на любом современном компьютере. Однако, к сожалению, ни один из четырех рекомендуемых статистических критериев не реализован в Excel12, поэтому можно посоветовать производить расчет
11Понятно,чтоприводимыеграницычисларазличающихсямеждусобойзначений–10,иобъемавыборок–50,примерны,приблизительны.
12ВкомпьютернойпрограммеMicrosoftExcelдляWindowsимеетсякритерийсогласияc2,отличающийсяотописанногонижекритерияоднородностиc2,поэтомуприменениепервогоможет привестикневерным результатам.
эмпирических значений критериев вручную
13 (все необходимые формулы приведены ниже), используя компьютер или калькулятор для получения описательной статистики и автоматизации расчетов. Аль- тернативой является использование компьютерной программы "Статистика в педагогике", которую можно загрузить с адреса http://www.mtas.ru/uploads/stat.zip (2.9 Мб).
Методы обработки данных и примеры. Приведем методики анализа данных для выделенных вы- ше шести типовых задач (см. таблицу 5): описательная статистика, анализ совпадений и различий ха- рактеристик экспериментальной и контрольной групп на основании измерений, проведенных в поряд- ковой шкале или шкале отношений. В качестве иллюстрации рассмотрим реализацию этих методик для числового примера (см. таблицы 1 и 4).
Описательная статистика. В практических задачах обычно имеется совокупность наблюдений (десятки, сотни, а иногда – тысячи результатов измерений индивидуальных характеристик), поэтому возникает задача компактного описания имеющихся данных. Для этого используют методы описатель-ной статистики – описания результатов с помощью различных агрегированных показателей и графи- ков. Кроме того, некоторые показатели описательной статистики используются в статистических крите- риях при определении достоверности совпадений и/или различий характеристик экспериментальной и контрольной группы.
Для результатов измерений в шкале отношений (задача 1.1 – см. таблицу 5) показатели описатель- ной статистики можно разбить на несколько групп:
Рассмотрим методы решения типовых для педагогических исследований задач анализа данных.
Алгоритм выбора статистического критерия. Поясним, как следует выбирать статистические критерии, то есть приведем алгоритм выбора статистического критерия – процедуру принятия решения относительно того, какой статистический критерий использовать в той или иной ситуации.
В первом приближении этот алгоритм чрезвычайно прост: если данные получены в результате измерений в шкале отношений, то следует использовать критерий Вилкоксона-Манна-Уитни (ВМУ), если в порядковой шкале, то критерий c 2.
Возможные модификации этого правила принятия решений (учитывающие большее число факто- ров) приведены на рисунке 1.
Во-первых, необходимо определить какая шкала измерений используется – отношений или поряд- ковая.
Для шкалы отношений следует решить, состоит ли решаемая задача в обнаружении различия сред- них значений (математических ожиданий). Если – да, то можно использовать критерий Крамера-Уэлча (описание методик применения всех упоминаемых статистических критериев приведено ниже). Если же следует обнаружить произвольные различия характеристик выборок, то следует использовать критерий Вилкоксона-Манна-Уитни или критерий 2.
Если число различающихся между собой значений10 в сравниваемых выборках велико (более деся- ти), то целесообразно использование критерия Вилкоксона-Манна-Уитни.
9Встречаютсяслучаи,когдаимеетсянесколькоэкспериментальныхилинесколькоконтрольныхгрупп.Приэтомпопарноеих сравнениевсеравноявляетсяодной из базовыхзадач.
10Например,выборка(1,2,2,2, 1, 1, 2,1, 1, 1) содержитвсегодваразличныхзначения–единицуидвойку.Втожевремя,
например,выборка (2,0,1,5,8,4,2,7,3,9) того жеобъема(десять элементов) содержитдесять различныхзначений.
Если число различающихся между собой значений в сравниваемых выборках мало (менее десяти), то, произведя группировку результатов измерений (то есть, перейдя от шкалы отношений к порядковой шкале – см. выше пятый раздел), можно использовать критерий 2.
Далее, аналогично рассуждая, если объем выборок мал11 (N, M 50), то следует использовать кри- терий Вилкоксона-Манна-Уитни (при малом числе различающихся значений в этом случае можно ис- пользовать и критерий 2).
Если объем выборок велик, то, опять же с помощью группировки результатов измерений, имеет смысл использовать критерий 2. | Проверка совпадения средних | Проверка совпадения всех показателей | |
| |  | |
| Объем | Объем | Объем |
| выборки | выборки | выборки |
| велик | велик | мал |
| N,M>50 | N,M>50 | N,M50 |
Рис.1.Алгоритмвыборастатистическогокритерия Для порядковой шкалы в случае, когда число градаций (различных баллов) больше либо равно трем, используется критерий 2, если же применялась дихотомическая шкала, то можно использовать либо критерий 2, либо критерий Фишера.
Использование компьютера при анализе результатов педагогических экспериментов, несомненно, целесообразно. Однако использовать статистические критерии, "зашитые" в пакеты программ следует осторожно. Все четыре предлагаемых к использованию для обработки результатов педагогического эксперимента статистических критерия (Крамера-Уэлча, Вилкоксона-Манна-Уитни, 2 и Фишера) кор- ректно реализованы в профессиональных статистических пакетах, среди которых можно выделить и рекомендовать такие наиболее распространенные пакеты статистического анализа как: Statistica, StatGraphics и SPSS. Однако, упомянутые программы, во-первых, являются лицензионными и стоят достаточно дорого. Во-вторых, они достаточно сложны и требуют значительных временных затрат для своего освоения. Наряду с этим, существуют инструменты статистического анализа в электронных таблицах Microsoft Excel, входящих в стандартный комплект Microsoft Office и установленных, навер- ное, на любом современном компьютере. Однако, к сожалению, ни один из четырех рекомендуемых статистических критериев не реализован в Excel12, поэтому можно посоветовать производить расчет
11Понятно,чтоприводимыеграницычисларазличающихсямеждусобойзначений–10,иобъемавыборок–50,примерны,приблизительны.
12ВкомпьютернойпрограммеMicrosoftExcelдляWindowsимеетсякритерийсогласияc2,отличающийсяотописанногонижекритерияоднородностиc2,поэтомуприменениепервогоможет привестикневерным результатам.
эмпирических значений критериев вручную
13 (все необходимые формулы приведены ниже), используя компьютер или калькулятор для получения описательной статистики и автоматизации расчетов. Аль- тернативой является использование компьютерной программы "Статистика в педагогике", которую можно загрузить с адреса http://www.mtas.ru/uploads/stat.zip (2.9 Мб).
Методы обработки данных и примеры. Приведем методики анализа данных для выделенных вы- ше шести типовых задач (см. таблицу 5): описательная статистика, анализ совпадений и различий ха- рактеристик экспериментальной и контрольной групп на основании измерений, проведенных в поряд- ковой шкале или шкале отношений. В качестве иллюстрации рассмотрим реализацию этих методик для числового примера (см. таблицы 1 и 4).
Описательная статистика. В практических задачах обычно имеется совокупность наблюдений (десятки, сотни, а иногда – тысячи результатов измерений индивидуальных характеристик), поэтому возникает задача компактного описания имеющихся данных. Для этого используют методы описатель-ной статистики – описания результатов с помощью различных агрегированных показателей и графи- ков. Кроме того, некоторые показатели описательной статистики используются в статистических крите- риях при определении достоверности совпадений и/или различий характеристик экспериментальной и контрольной группы.
Для результатов измерений в шкале отношений (задача 1.1 – см. таблицу 5) показатели описатель- ной статистики можно разбить на несколько групп:
-
показатели положения описывают положение экспериментальных данных на числовой оси. При- меры таких данных – максимальный и минимальный элементы выборки, среднее значение14, медиана15, мода16 и др.; -
показатели разброса описывают степень разброса данных относительно своего центра (среднего значения). К ним относятся: выборочная дисперсия17, разность между минимальным и максимальнымэлементами(размах, интервалвыборки) и др. -
показателиасимметрии: положение медианы относительно среднего и др. -
гистограмма18 и др.