Файл: Математическая статистика и её роль в медицине и здравоохранении.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 42
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Практика №1
Тема: «Математическая статистика и её роль в медицине и здравоохранении»
Задание
-
Освоить материал. -
Задачи для самостоятельного решения выполнить в рабочей тетради. -
Выполнить проверочную работу по вариантам в отдельной тетради для контрольных работ (студенты1 подгруппы выполняют задания Варианта №1, студенты 2 подгруппы – задания Варианта №2). -
Выполнить письменно задачи домашней работы в рабочей тетради.
ПЛАН
1. Кодирование статистических данных
2. Построение статистического распределения выборки
3. Построение полигонов и гистограмм
4. Проведение интервальной оценки
Математическая статистика-это раздел математики, изучающий методы сбора, систематизации и обработки результатов наблюдений случайных массовых явлений, с целью выявления существующих закономерностей.
Т.О.
-
В центре внимания математической статистики - массовые явления. -
Единственный способ получения информации - проведение эксперимента. -
Все характеристики случайных процессов и явлений получаются по экспериментальным данным.
Наблюдаемые значения рассматриваемого признака X называют вариантами ( обозначение :
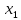 ,
,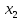 ,…
,…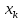 ).
).Последовательность вариант в порядке возрастания(убывания) называется вариационным рядом.
Объем выборки - это сумма частот вариант, то есть
N=
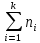 ,
,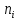 -частота варианты
-частота варианты 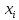 , где значение
, где значение 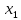 признака Х наблюдалось
признака Х наблюдалось 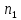 раз,
раз,значение x2 признака Х наблюдалось n2 раз и т.д.
Числа
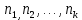
называются частотами вариант
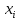 .
.Относительная частота варианты
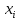 это отношение частоты варианты к объёму выборки.
это отношение частоты варианты к объёму выборки.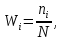 где
где 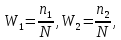 …,
…,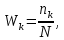
Статистическими распределениями выборки называется таблица, вида
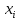 |  |  | … |  | -вариационный ряд |
 |  | 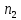 | … | 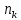 | N= 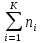 |
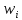 | 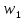 | 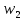 | … | 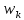 | 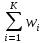 = 1 = 1 |
Замечание. Зашифровать статистические данные – это значит построить статистическое распределение выборки, т.е. таблицу указанного вида.
-
Геометрическая интерпретация статистического распределения выборки.
Полигоны – ломанные в первой четверти системы координат, соединяющие точки с координатами:
-
для полигона частот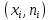
-
Для полигона относительных частот ( xi ,w i)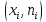
Гистограммы-столбчатые фигуры в системе координат (в первой четверти), состоящие из тесно примыкающих друг к другу прямоугольников, разных высот.
-
для гистограмма частот (высоты соответствуют частотам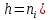
-
для гистограмма относительных частот (высоты соответствуют относительным частотам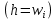
Зам: Варианты задаются интервалами: конец предыдущего является началом последующего.
Интервальная оценка – это оценка таких показателей, как:
-
выборочное и генеральное среднее -
выборочная и генеральная дисперсии -
среднеквадратическое отклонение.
Выборочным средним
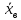 выборки объёма N со статистическим распределением вида
выборки объёма N со статистическим распределением вида  |  |  | … |  |
 |  |  | … |  |
называется среднее арифметическое значений признака выборки, т.е.
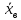 =
= 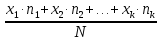
=
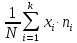
Генеральное среднее
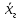 генеральной совокупности объёма N со статистическим распределением вида
генеральной совокупности объёма N со статистическим распределением вида  |  |  | … |  |
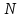 | 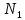 | 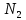 | … | 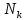 |
называется среднее арифметическое значений признака генеральной совокупности, т.е.
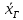 =
= 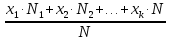 =
= 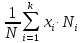
Выборочной дисперсией
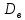 некоторой выборки называется среднее арифметическое квадратов отклонений значений признака от выборочной средней
некоторой выборки называется среднее арифметическое квадратов отклонений значений признака от выборочной средней . Если варианты x1,
. Если варианты x1,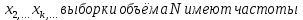 n1 , n2, …nk , то
n1 , n2, …nk , то 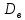 =
= 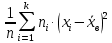
Аналогично для генеральной совокупности определяют генеральную дисперсию
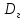 =
= 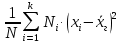
Дисперсия является характеристикой рассеяния значений вокруг своего среднего значения.
Среднеквадратическое отклонение
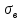
=
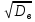 измеряется в тех же единицах, что и изучаемый признак.
измеряется в тех же единицах, что и изучаемый признак.1. Кодирование статистических данных.
ПРИМЕР 1.1.
Закодировать статистические данные: 2,6,5,2,2,5,3,3,1,3,3,5
Решение.
Имеем:
 | 1 | 2 | 3 | 4 | 5 | 6 | вариационный ряд |
| ni | 1 | 2 | 4 | 0 | 3 | 1 | N=1+2+4+0+3+1=11 |
| wi | 1/11 | 2/11 | 4/11 | 0 | 3/11 | 1/11 | 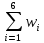 = 1 = 1 |
2. Построение статистического распределения выборки
ПРИМЕР 2.1. Ежедневное количество студентов, посещающих методический кабинет на протяжении ряда дней, следующее:
15,17, 16,18,20,21, 18, 17,20, 15,
18,17,16,19,17,16,18,19,18,19.
Составить статистическое распределение выборки.
Решение. В первой строке таблицы укажем встречающиеся значения посещений, во второй — количество таких значений и, наконец, в третьей — относительную частоту этих значений.
| Значения признака хi | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| Частота встречаемости ni | 2 | 3 | 4 | 5 | 3 | 2 | 1 |
| Относительная частота wi | 0,1 | 0,15 | 0,2 | 0,25 | 0,15 | 0,1 | 0,05 |