Файл: Математическая статистика и её роль в медицине и здравоохранении.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 11.12.2023

Просмотров: 43

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.


3. Построение полигонов и гистограмм.
ПРИМЕР 3.1. Дано: статистическое распределение выборки

Интервал
14,5-15,5
15,5-16,5
16,5-17,5
17,5-18,5
18,5-19,5
19,5-20,5
20,5-21,5

mi
2
3
4
5
3
2
1

fi
0,1
0.15
0,2
0,25
0,15
0,1
0,05

Построить полигон и гистограмму относительных частот




Решение


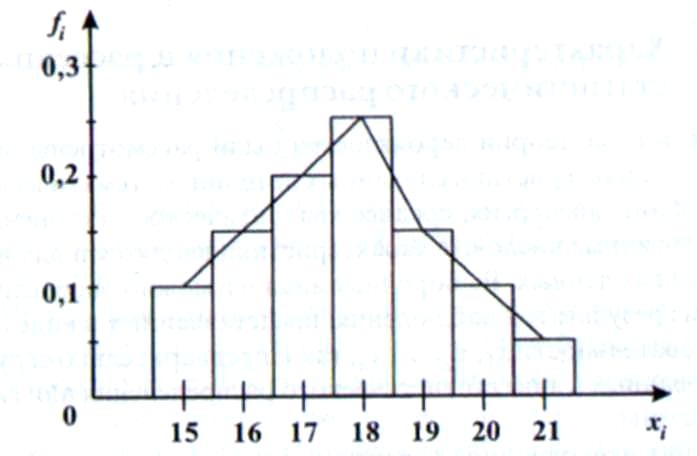
Полигон частот можно получить из гистограммы путем соединения срединных значений классов. График полигона частот (или относительных частот) легко постро­ить и по статистическому распределению. На оси вариант (О ), из точек хiпроводятся перпендикуляры высотой и со­единяются ломаной линией.

При неограниченном увеличении числа наблюдений и увеличении количества классов ширина прямоугольников гистограммы будет уменьшаться и середины верхних кон­цов прямоугольников сольются в одну сплошную плав­ную линию, которая в пределе станет графиком плотности.
4. Интервальная оценка
ПРИМЕР 4.1. Имеется выборка: 2, 4, 5, 3, 6, 4. Найти выборочную среднюю, выборочную дисперсию и ошибку выборочной средней.

Решение


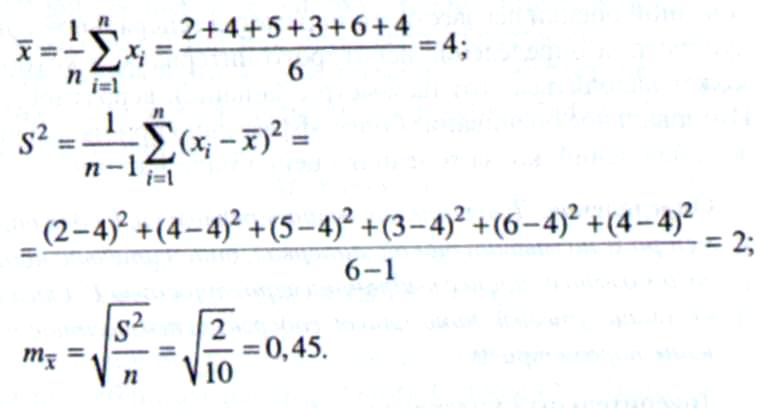
ПРИМЕР 4.2. Из генеральной совокупности извлечена выборка:


хi
4
5
6
7

mi
10
12
6
2


Найти оценки математического ожидания и дисперсии.

Решение



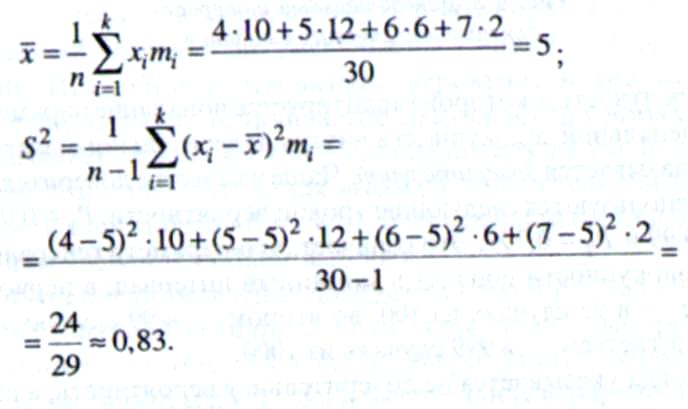
ПРИМЕР 4.3. Для данных примера 4.2. найти довери­тельный интервал математического ожидания с вероятно­стью 0,95.

Решение

Из решения примера 4.2. имеем:



В таблице Стьюдента найдем .

Тогда:



Задачи для самостоятельного решения

1. Значение случайной величины X представлены в виде статистического распределения:


Значения X
Частота
Значения X
Частота

120-140

140-160

160-180

180-200
1

6

19

58
200-220

220-240

240-260

260-280
53

24

16

3

Найти выборочную среднюю и выборочную дисперсию.

2. Из генеральной совокупности извлечена выборка объемом п = 50.

Xi
2
5
7
10



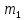16
12
8
14

Найти оценки математического ожидания и генеральной дисперсии.

3. Пять измерений некоторой величины дали следующие результаты: 92, 94, 103, 105, 106. Найти выборочную сред­нюю и выборочную дисперсию.

4. Из общего числа студентов выборочно измерен рост у 81 мужчины. Средний рост оказался равным 171 см с дис­персией
S2 = 64 см2. Определить ошибку выборочной сред­ней и коэффициент вариации.

5. Признак X генеральной совокупности распределен нормально. Данные выборки имеют следующее статисти­ческое распределение:

Xi
0,1
0,2
0,3
0,4
0,5



2
4
7
6
1

Найти выборочную среднюю х и выборочное среднее квадратическое отклонение S.

6. Количественный признак X распределен нормаль­но. По выборке объемом 18 найдено выборочное среднее значение 21,5 и среднее квадратическое отклонение S = 0,9. Найти коэффициент вариации, ошибку выборочной сред­ней и доверительный интервал для математического ожи­дания при уровне значимости а < 0,05.

7. В ходе проведенных исследований изучен рост муж- - чин 25 лет из сельской местности. Объем выборки п = 21. По данным статистической обработки, имеем:

Границы интервалов (см)
161-165
165-169
169-173
173-177
177-181

Относительная

частота
0,06
0,19
0,47
0,19
0,09




  1. Изучено воздействие определенной физиопроцеду­ры на частоту сердечных сокращений в группе испытуемых. Объем выборки 18. По данным статистической обработки имеем:



Границы

интервалов

(уд./мин)
67-68,2
68,2-69,4
69,4-70,6
70,6-71,8
71,8-73

Относитель­ная частота
0,05
0,2
0,44
0,26
0,05

Выборочная средняя 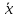= 70,16; выборочное среднеквад­ратическое отклонение S = 1,2. Построить гистограмму и определить доверительный интервал для математического ожидания с уровнем значимости α≤ 0,05.

ПРОВЕРОЧНАЯ РАБОТА
Вариант №1

1.Закодировать статистические данные: 3,5, 1,1,2,1, 2, 3, 3, 5, 3 и построить полигоны а) частот; б) относительных частот.

2. Дано: статистическое распределение выборки типа:
5-8
8-10
10-12
12-15



2
8
1
6

Построить гистограмму частот.

  1. Имеется выборка: 2,1, 4, 5, 3,5, 4. Найти выборочную среднюю, выборочную дисперсию и ошибку выборочной средней.



Вариант №2

1.Закодировать статистические данные: 3,5, 1,3,2,1, 3, 4, 5 и построить полигоны а) частот; б) относительных частот.

2. Дано: статистическое распределение выборки типа:
4-6
6-11
11-12
12-15



3
6
7
1

Построить гистограмму частот.

3.Имеется выборка: 2,2, 4, 5, 3,5, 1. Найти выборочную среднюю, выборочную дисперсию и ошибку выборочной средней.

Домашнее задание

1. В результате испытания случайная величина X при­няла следующие значения: 2, 6, 8, 4, 2, 5, 7, 6, 4, 4, 1, 5, 7, 6, 3, 1, 3, 5, 5, 3. Построить дискретный вариационный ряд и начертить полигон распределения.

2. В результате испытания случайная величина X при­няла следующие значения: 11, 13, 18,22,24, 12,23, 15,18, 17 12, 18, 19, 20, 12, 22, 16, 17, 14, 20, 21, 25, 27, 19.Построить дискретный вариационный ряд с равными интервалами и начертить гистограмму.

3. Дан вариационный ряд: 3, 6,6, 8, 8,12,12,12,25,25, 70, 75. Найти выборочную среднюю и выборочную дисперсию.
4. Выборочная средняя = 171,42; выборочное среднеквадратическое отклонение


= 3,6. Построить гистограм­му распределения частот и определить доверительный ин­тервал для математического ожидания с доверительной ве­роятностью р ≥ 0,95.

Смотрите также файлы