Файл: Практикум волгоград 2014 Печатается по решению редакционноиздательского совета.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 254
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
от задней преломляющей поверхности до заднего фокуса.
4.8. Отложив отрезки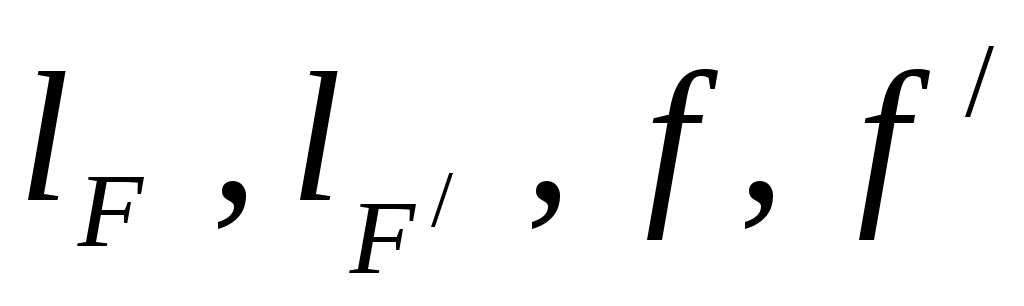 (см. формулы (19) – (21)), найти положения фокусов и главных точек объектива относительно преломляющих поверхностей.
(см. формулы (19) – (21)), найти положения фокусов и главных точек объектива относительно преломляющих поверхностей.
4.9. Повторить п.4.1 – 4.8 не менее пяти раз. Провести статистическую обработку результатов с доверительной вероятностью 90%.
4.10. По предоставленным преподавателем данным о параметрах линз и их расположении в оптической системе объектива рассчитать положения его кардинальных элементов. Изобразить полученные результаты на рисунке. Сравнить экспериментальные и расчетные результаты.
5. Контрольные вопросы и задания
1. Дайте определения кардинальных элементов оптической системы. Объясните физический смысл главных и фокальных плоскостей и точек.
2. Выведите формулы (33) – (37).
3. Может ли двояковогнутая линза быть собирающей? Может ли двояковыпуклая линза быть рассеивающей?
4. Две собирающие линзы с фокусными расстояниями f1 и f2 установлены на расстоянии L друг от друга, так что их оптические оси совпадают. Найти фокусное расстояние этой системы линз.
5. Фокусное расстояние тонкой стеклянной линзы в воде равно f. При погружении ее в сероуглерод (n=1,63) фокусное расстояние изменилось на f. Чему равны фокусное расстояние линзы и показатель преломления стекла?
6. Расстояние между двумя точечными источниками равно L. Где нужно поместить собирающую линзу с фокусным расстоянием f, чтобы изображения обоих источников совпали?
7. С помощью тонкой собирающей стеклянной линзы с показателем преломления n=1,5 получено действительное изображение предмета на расстоянии 10 см от линзы. После того как предмет и линзу поместили в воду, не меняя расстояния между ними, изображение получилось на расстоянии 60 см от линзы. Найти фокусное расстояние линзы в воздухе, если показатель преломления воды nв = 1,33.
8. Двояковыпуклая линза с радиусами кривизны поверхностей r1= 6 см и r2= ‑3 см, толщиной по оси =1,5 см, показателем преломления n=1,5 находится в воздухе. Найти фокусное линзы и расположение кардинальных плоскостей.
9 . Из плоскопараллельной стеклянной пластинки изготовлены три линзы (см. рис.). Фокусное расстояние линз 1 и 2, сложенных вместе, равно –f12, фокусное расстояние линз 2 и 3 равно –f23. Определить фокусное расстояние каждой линзы.
1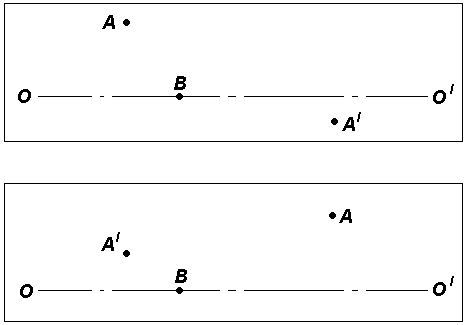
0. На рисунках указано положение оптической оси, предмета А и его изображения А/. Определить положение линзы и ее фокусов.
Построить изображение точки В.
11. Оптическая сила тонкой линзы в воздухе и в жидкости с неизвестным показателем преломления равна соответственно Ф0 и –Ф1. Чему равен показатель преломления жидкости, если у стекла линзы он равен n?
1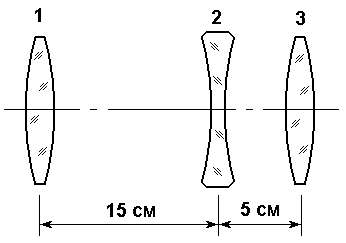
2. Найти положение кардинальных элементов системы с тонкими линзами, показанной на рисунке, если f1= 10 см, f2= ‑20 см. f3= 9 см.

ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА
НА ГРАНИЦЕ ДВУХ СРЕД
Лабораторная работа
ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА НА ГРАНИЦЕ ДВУХ СРЕД
(ФОРМУЛЫ ФРЕНЕЛЯ)
ЦЕЛЬ РАБОТЫ: Изучение законов и исследование отражения и прохождения световых электромагнитных волн (ЭМВ) на границе раздела двух сред; анализ амплитудных и энергетических коэффициентов отражения и пропускания ЭМВ на этой границе; освоение методов юстировки оптических систем с использованием лазера.
ПРИНАДЛЕЖНОСТИ: оптическая скамья, маломощный непрерывный лазер, диафрагма, стеклянная плоскопараллельная пластина, укрепленная на лимбе, фотоприемник.
Электромагнитная волна, падая на границу раздела двух сред, частично отражается от поверхности раздела и частично преломляется, переходя во вторую среду. Физические явления, имеющие место в этом случае, следует прежде всего охарактеризовать энергетически, вводя понятие коэффициентов отражения и пропускания. Но необходимо исследовать и фазовые соотношения на границе двух сред. Это позволит получить новую информацию об изучаемых физических явлениях.
1.1. Законы отражения и преломления электромагнитных волн
Граничные условия для векторов поля световой волны на границе между двумя диэлектриками при отсутствии свободных зарядов и токов проводимости имеют вид:
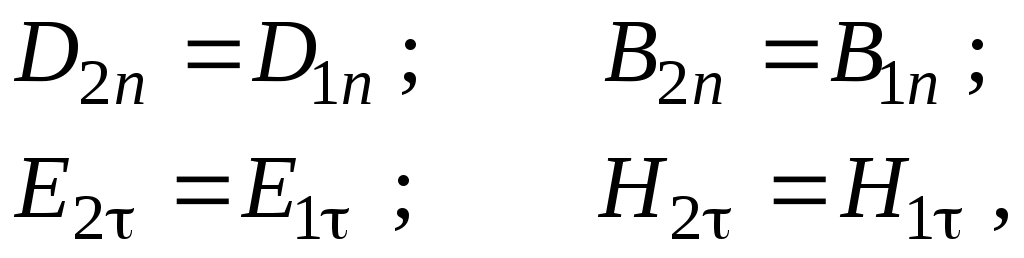 (1) – (2)
(1) – (2)
где t, n – индексы тангенциальных (касательных к границе раздела) и нормальных компонент векторов соответственно. Пусть на плоскую границу двух диэлектриков с абсолютными (не относительными!) проницаемостями (e1 ; m1) и (e2 ; m2) (магнитную проницаемость пока оставим в общем виде) падает под некоторым углом плоская световая волна (рис.1). Тогда для напряженностей электрического поля в падающей, отраженной и преломленной волнах соответственно имеем:
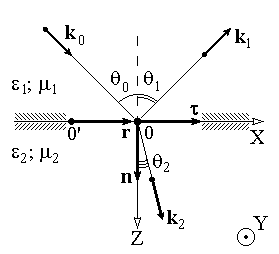
Рис. 1
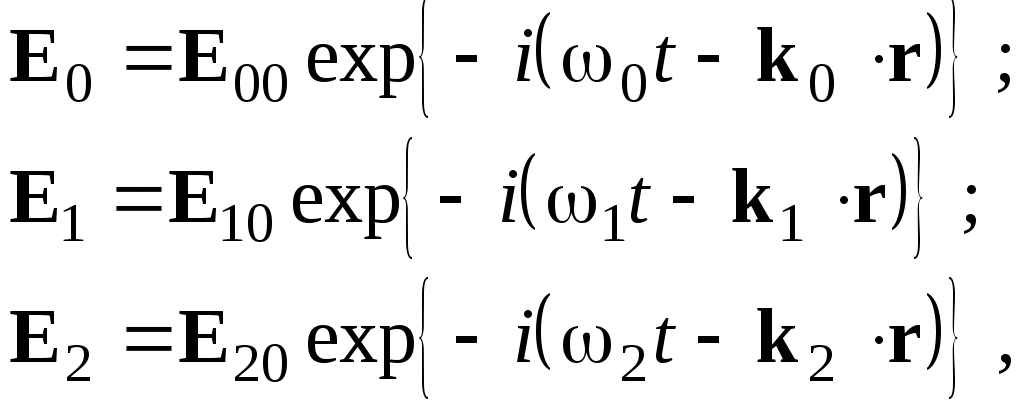 (3)
(3)
где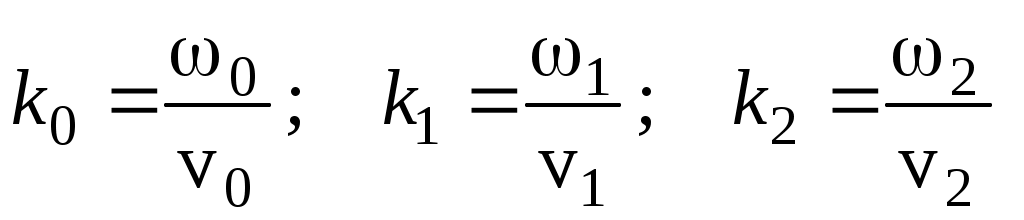
– волновые числа, причем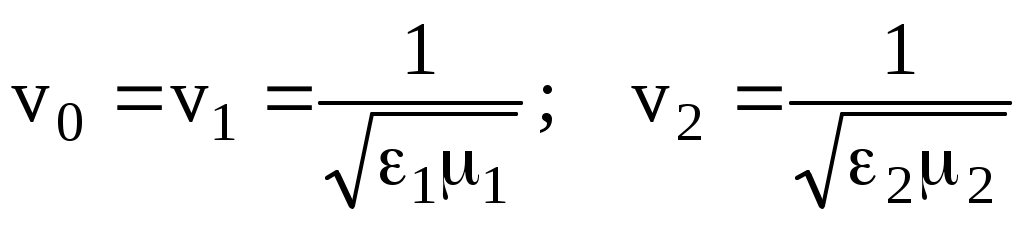 – скорости света в 1-й и 2-й средах.
– скорости света в 1-й и 2-й средах.
Законы отражения и преломления света на границе полностью определяются граничными условиями (1) и (2).
Для электрического поля с учетом (3) граничные условия принимают вид:
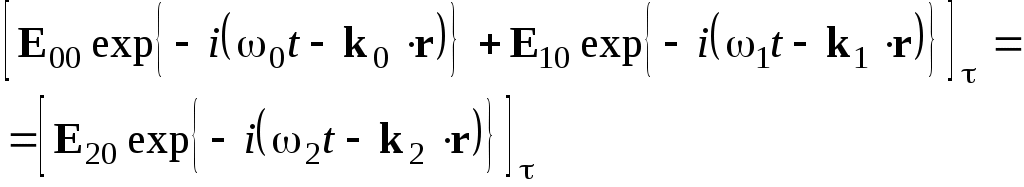 (4)
(4)
Отметим, что начало отсчета вектора r (точка 0’ ) совершенно произвольно. Если 0’ лежит не на поверхности раздела, то
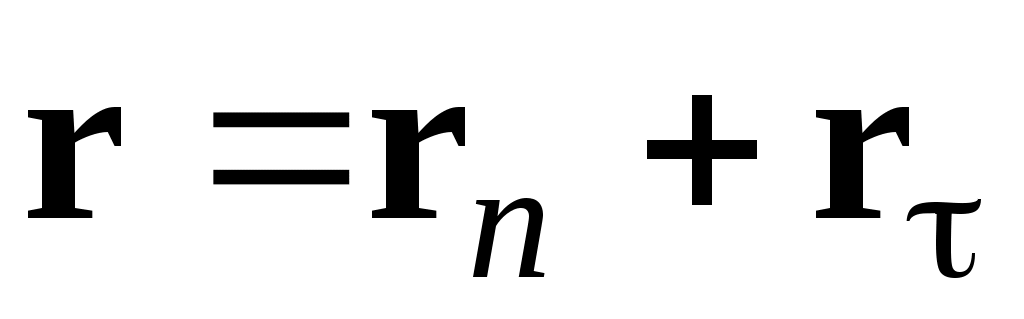 . (5)
. (5)
При этом в (4):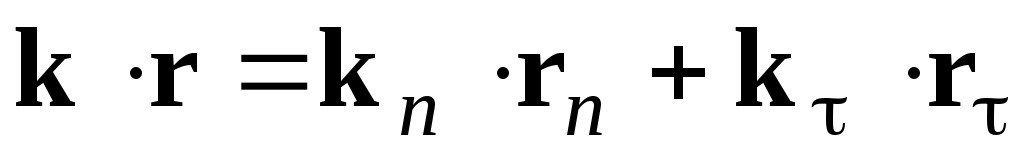 . Но для любой точки поверхности
. Но для любой точки поверхности 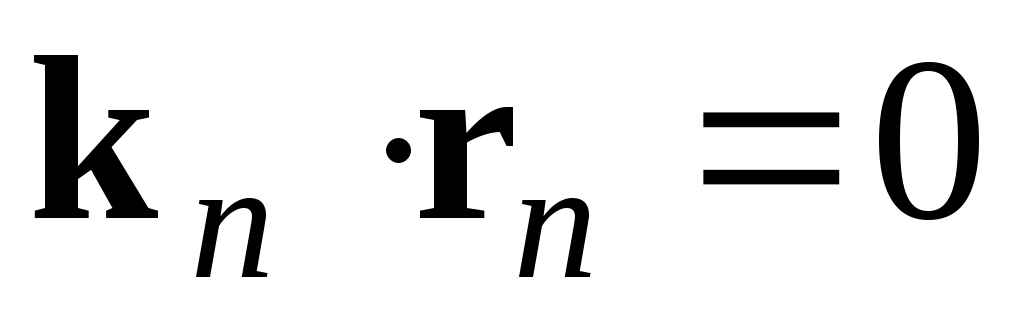 , поэтому удобно точку 0’ поместить на границе раздела.
, поэтому удобно точку 0’ поместить на границе раздела.
Равенство (4) будет соблюдаться для произвольных значений r и t только при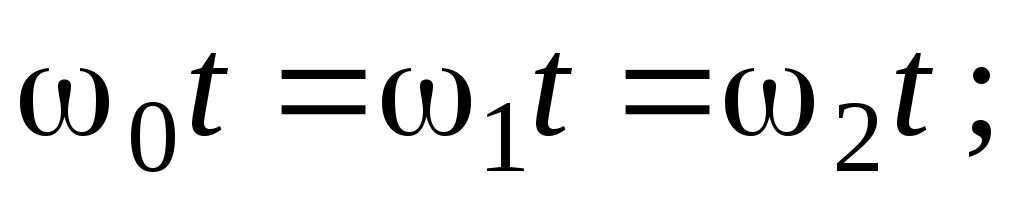 (6)
(6)
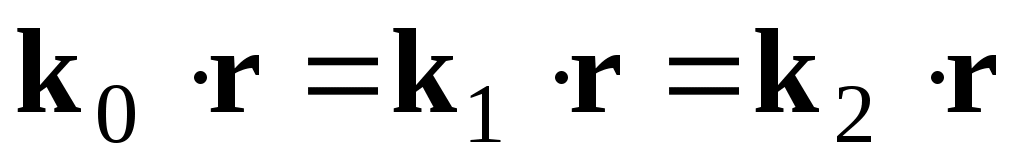 . (7)
. (7)
Отсюда следует, что частота ЭМВ при отражении и преломлении не меняется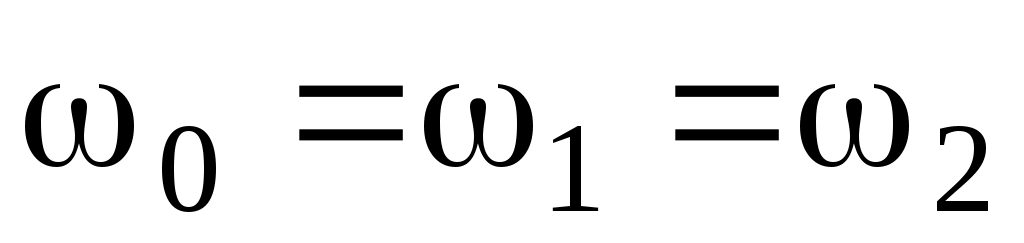 . (8)
. (8)
Выберем точку 0’ так, чтобы вектор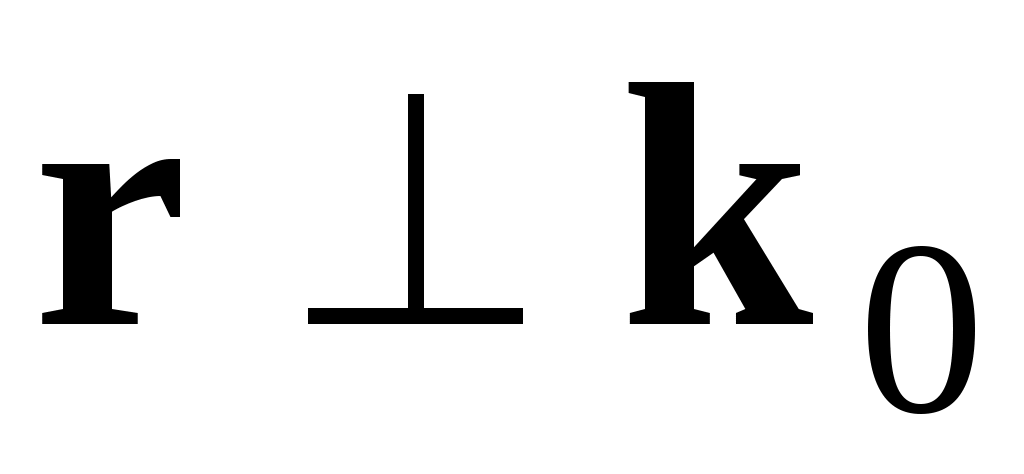 (т.е. направим перпендикулярно плоскости XZ рис.1). Тогда
(т.е. направим перпендикулярно плоскости XZ рис.1). Тогда 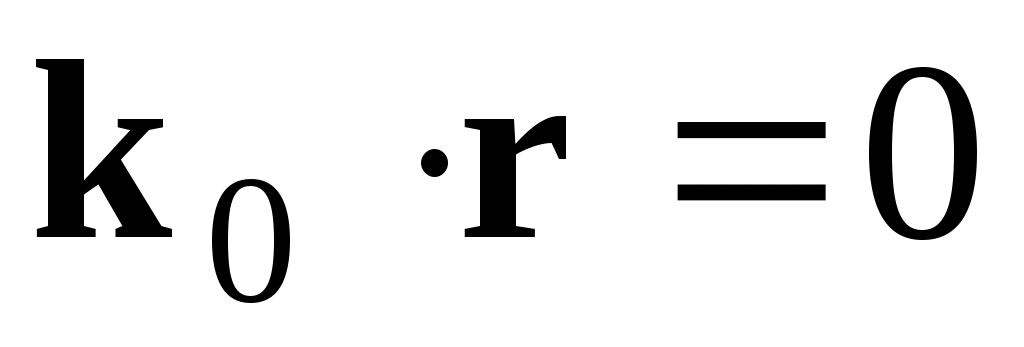 , а из (7) следует, что и
, а из (7) следует, что и 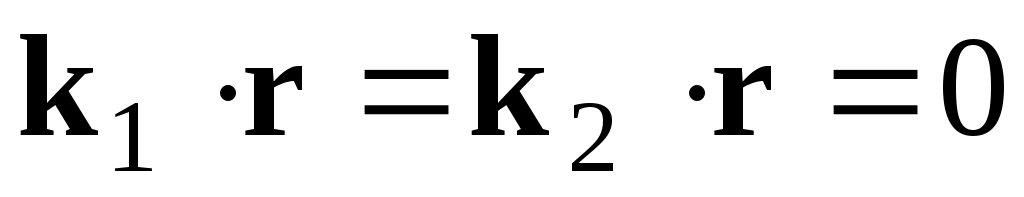 . Отсюда следует, что волновые векторы падающей, отраженной и преломленной волн (условно пока назовем направление k лучом) лежат в одной плоскости.
. Отсюда следует, что волновые векторы падающей, отраженной и преломленной волн (условно пока назовем направление k лучом) лежат в одной плоскости.
Плоскость, в которой лежат волновой вектор k0 и нормаль к поверхности раздела n в точке падения луча, называется плоскостью падения. Из рис.1 видно, что
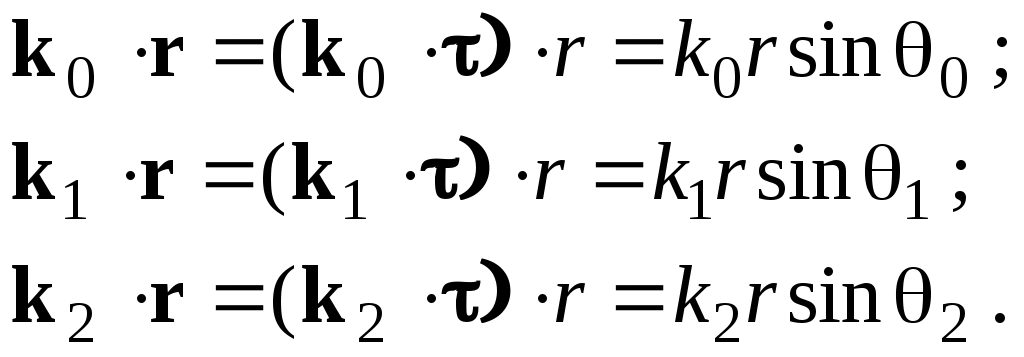 (9)
(9)
Тогда с учетом (7) получаем:
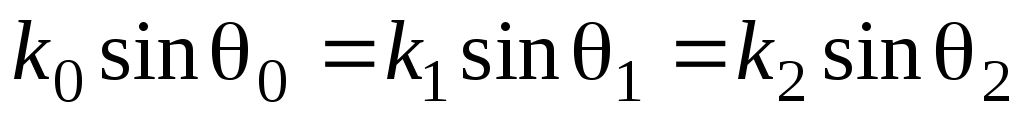 (10)
(10)
или из (3) и (8):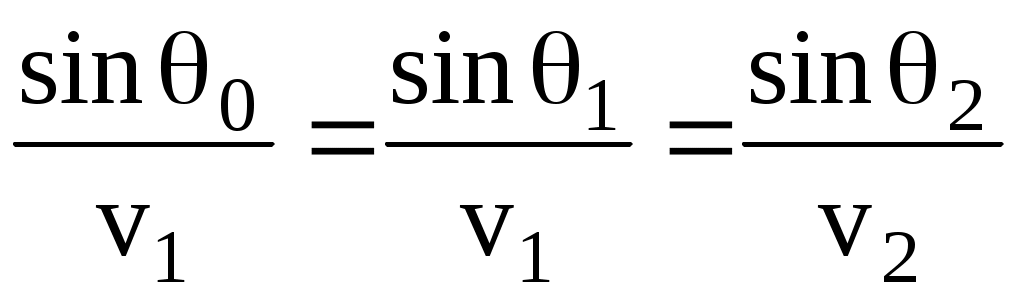 . (11)
. (11)
Вспомним, что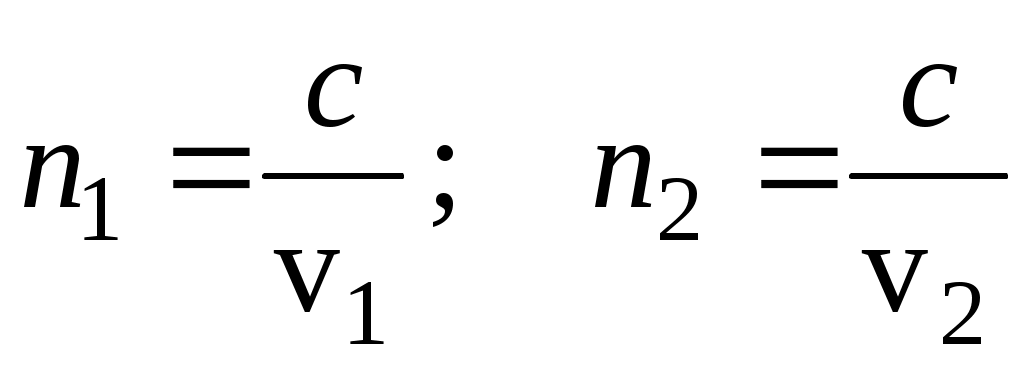
– показатели преломления. Из (11) можно сделать следующие выводы: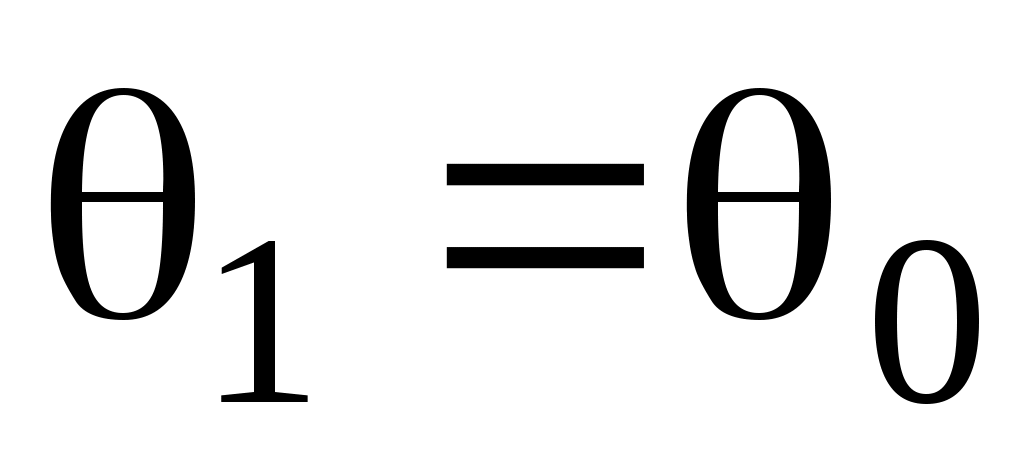 (12)
(12)
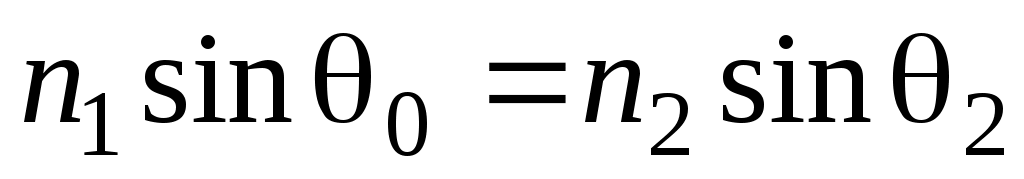 . (закон Снеллиуса) (13)
. (закон Снеллиуса) (13)
Введем обозначение
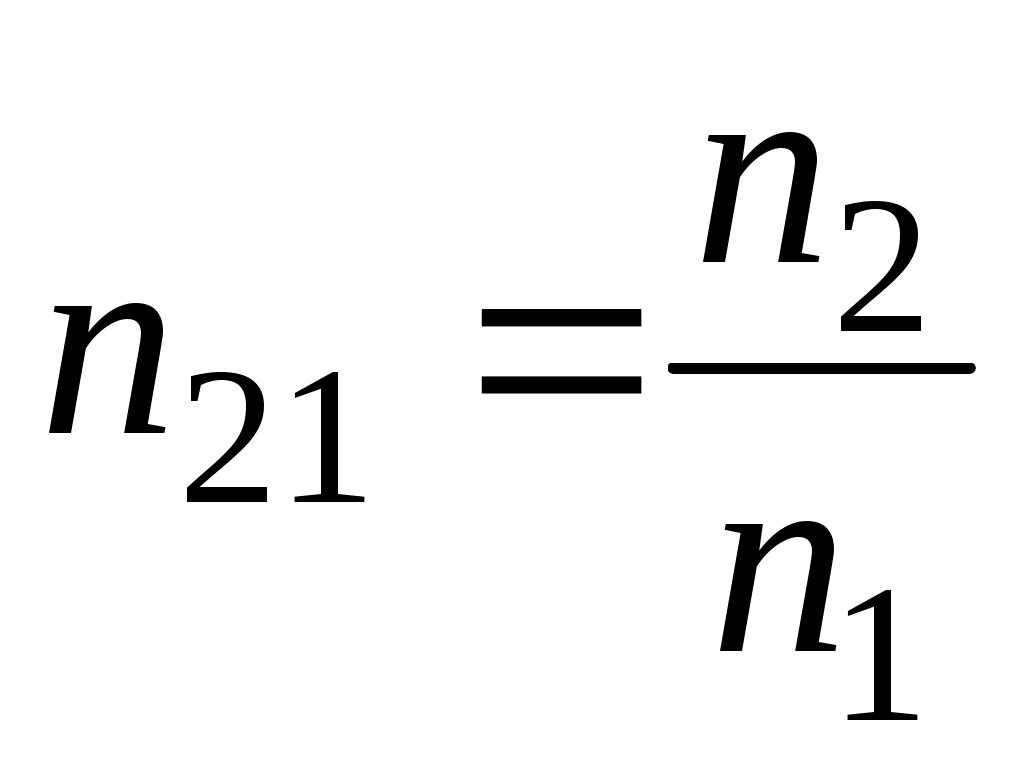 – относительный показатель преломления. (14)
– относительный показатель преломления. (14)
Тогда закон Снеллиуса примет вид:
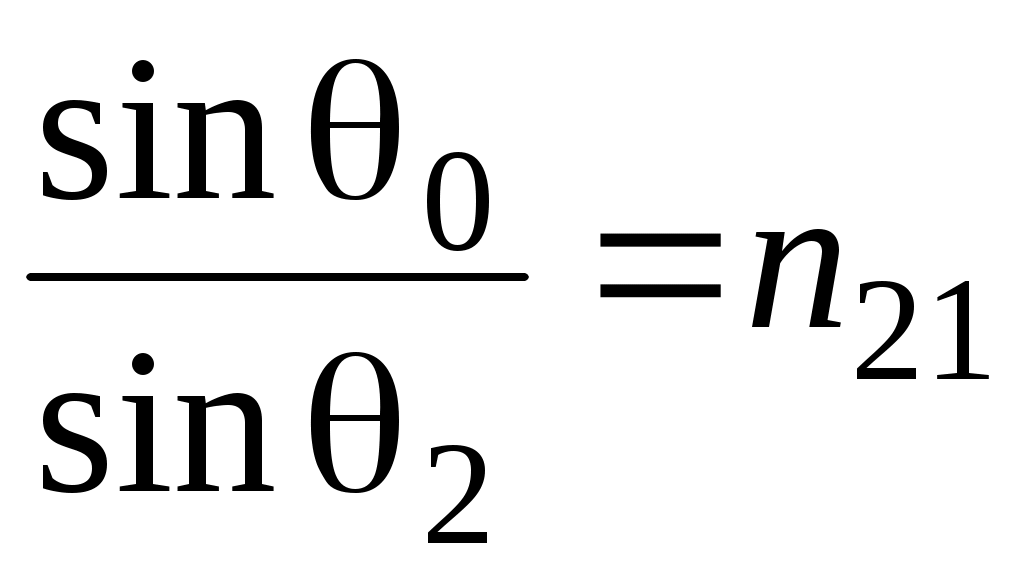 . (15)
. (15)
При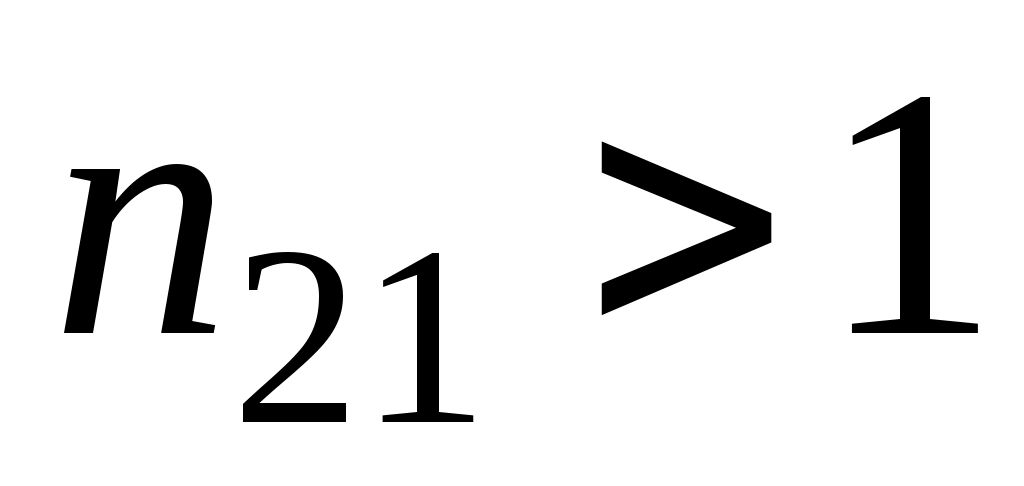 (падение из оптически менее плотной в оптически более плотную среду)
(падение из оптически менее плотной в оптически более плотную среду) 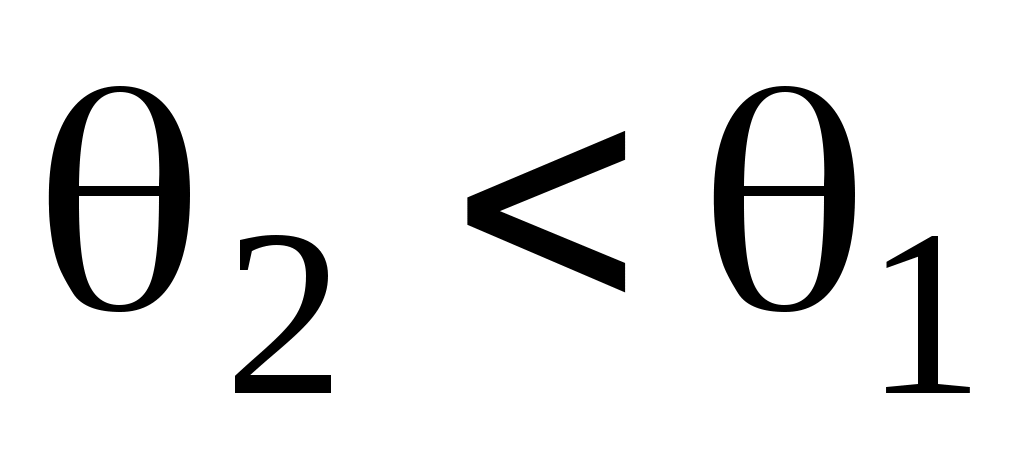 (рис.2). При
(рис.2). При 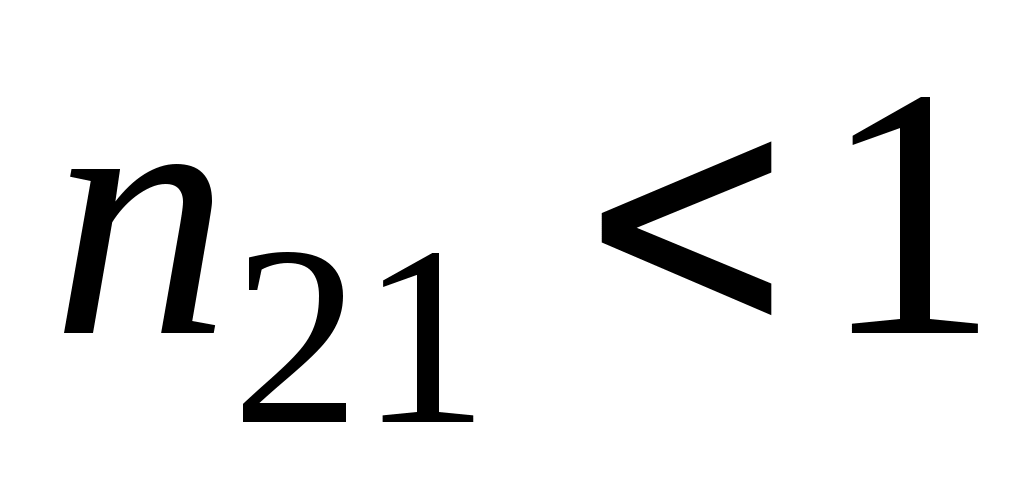
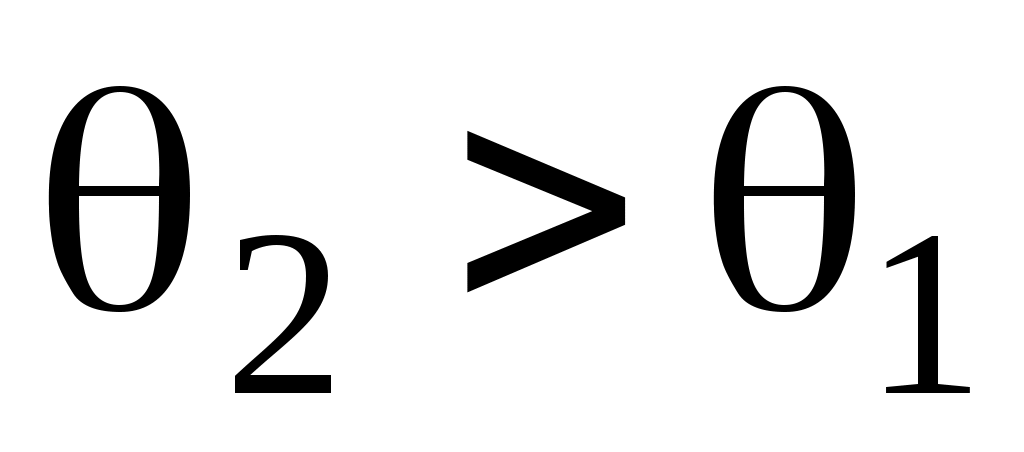 (рис.3).
(рис.3).
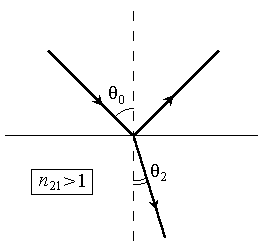
Рис. 2
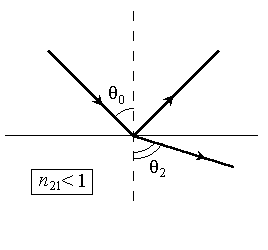
Рис. 3
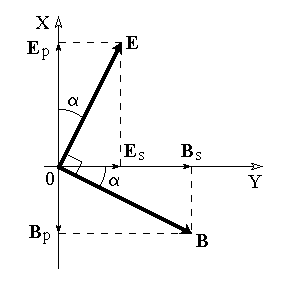 Рис. 4
Рис. 4
Вообще говоря, вектор E0 в падающей волне может иметь произвольный азимут a (угол между E и плоскостью падения. Разложим векторы электромагнитного поля на две составляющие: перпендикулярные плоскости падения (будем обозначать их индексом s (или ^) и параллельные плоскости падения (будем обозначать их индексом p (или || )) (рис.4):
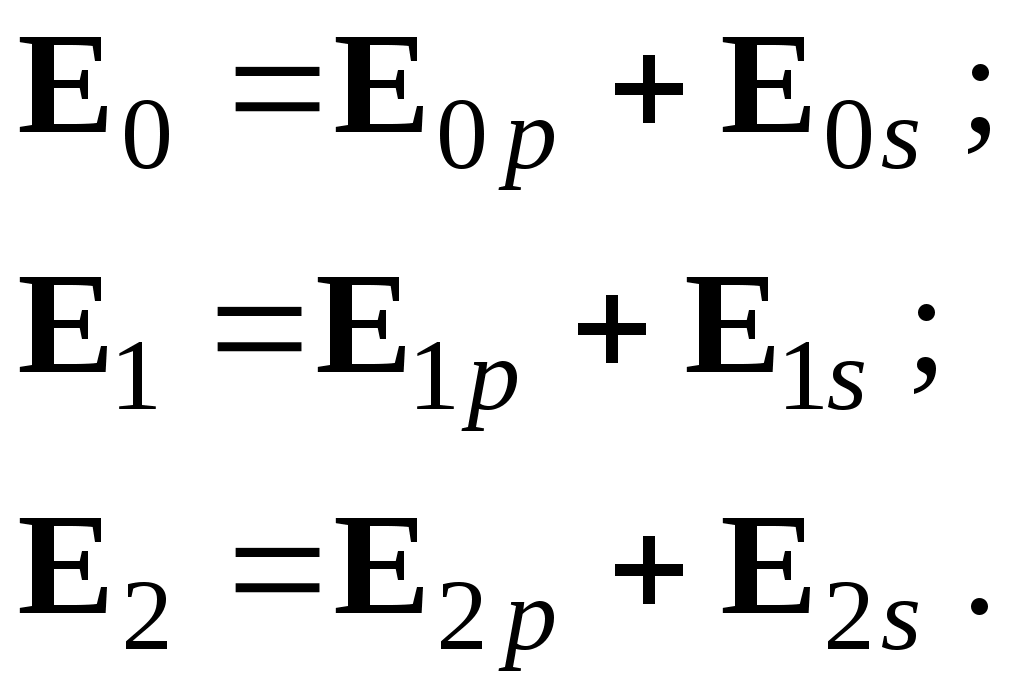 (16)
(16)
Видно, что векторы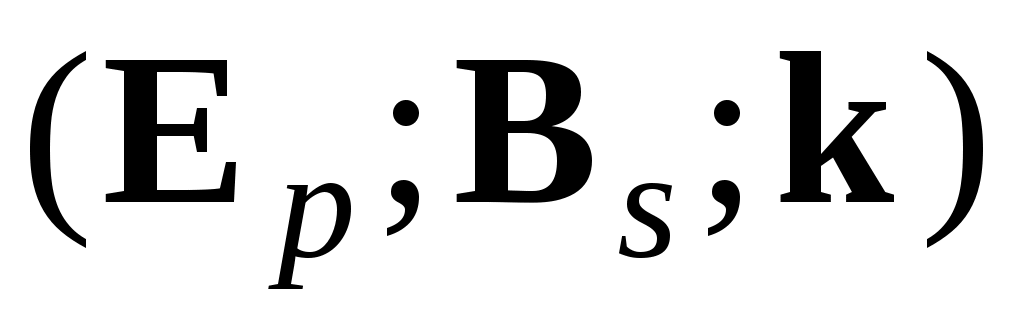 и
и 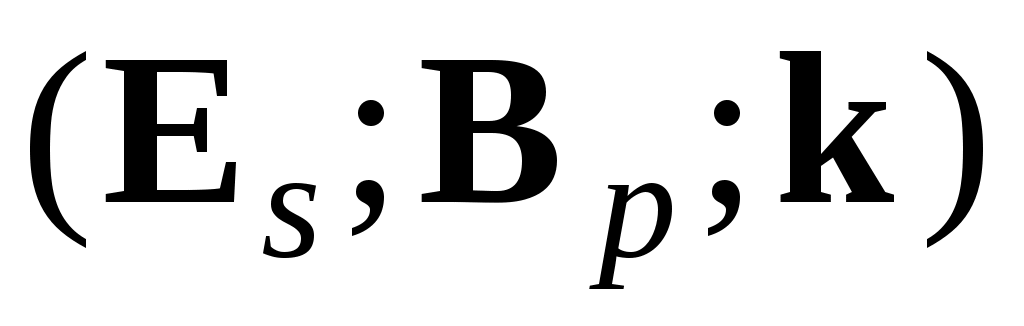 составляют правовинтовые тройки векторов и образуют сами плоские ЭМВ. Кроме этого видно, что
составляют правовинтовые тройки векторов и образуют сами плоские ЭМВ. Кроме этого видно, что 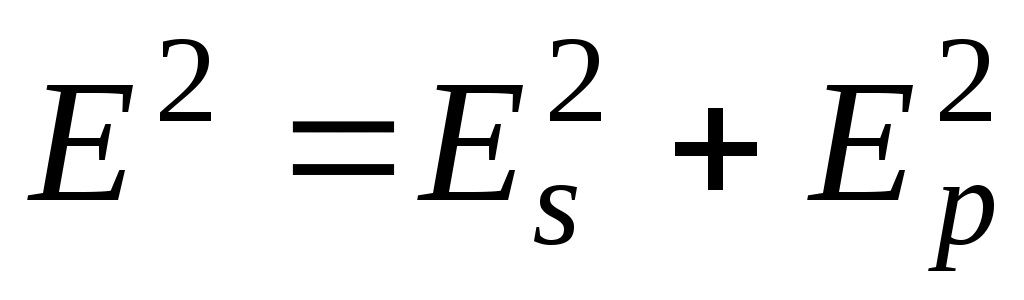 , т.е. плотность потока энергии исходной волны равна сумме плотностей потока энергии волн, на которые она разлагается.
, т.е. плотность потока энергии исходной волны равна сумме плотностей потока энергии волн, на которые она разлагается.
Т.о., плоскую волну с произвольным азимутом можно разложить на сумму волн, у одной из которых Ep (p – поляризация) лежит в плоскости падения, а у другой
4.8. Отложив отрезки
4.9. Повторить п.4.1 – 4.8 не менее пяти раз. Провести статистическую обработку результатов с доверительной вероятностью 90%.
4.10. По предоставленным преподавателем данным о параметрах линз и их расположении в оптической системе объектива рассчитать положения его кардинальных элементов. Изобразить полученные результаты на рисунке. Сравнить экспериментальные и расчетные результаты.
5. Контрольные вопросы и задания
1. Дайте определения кардинальных элементов оптической системы. Объясните физический смысл главных и фокальных плоскостей и точек.
2. Выведите формулы (33) – (37).
3. Может ли двояковогнутая линза быть собирающей? Может ли двояковыпуклая линза быть рассеивающей?
4. Две собирающие линзы с фокусными расстояниями f1 и f2 установлены на расстоянии L друг от друга, так что их оптические оси совпадают. Найти фокусное расстояние этой системы линз.
5. Фокусное расстояние тонкой стеклянной линзы в воде равно f. При погружении ее в сероуглерод (n=1,63) фокусное расстояние изменилось на f. Чему равны фокусное расстояние линзы и показатель преломления стекла?
6. Расстояние между двумя точечными источниками равно L. Где нужно поместить собирающую линзу с фокусным расстоянием f, чтобы изображения обоих источников совпали?
7. С помощью тонкой собирающей стеклянной линзы с показателем преломления n=1,5 получено действительное изображение предмета на расстоянии 10 см от линзы. После того как предмет и линзу поместили в воду, не меняя расстояния между ними, изображение получилось на расстоянии 60 см от линзы. Найти фокусное расстояние линзы в воздухе, если показатель преломления воды nв = 1,33.
8. Двояковыпуклая линза с радиусами кривизны поверхностей r1= 6 см и r2= ‑3 см, толщиной по оси =1,5 см, показателем преломления n=1,5 находится в воздухе. Найти фокусное линзы и расположение кардинальных плоскостей.
9 . Из плоскопараллельной стеклянной пластинки изготовлены три линзы (см. рис.). Фокусное расстояние линз 1 и 2, сложенных вместе, равно –f12, фокусное расстояние линз 2 и 3 равно –f23. Определить фокусное расстояние каждой линзы.
1

0. На рисунках указано положение оптической оси, предмета А и его изображения А/. Определить положение линзы и ее фокусов.
Построить изображение точки В.
11. Оптическая сила тонкой линзы в воздухе и в жидкости с неизвестным показателем преломления равна соответственно Ф0 и –Ф1. Чему равен показатель преломления жидкости, если у стекла линзы он равен n?
1

2. Найти положение кардинальных элементов системы с тонкими линзами, показанной на рисунке, если f1= 10 см, f2= ‑20 см. f3= 9 см.

ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА
НА ГРАНИЦЕ ДВУХ СРЕД
Лабораторная работа
ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА НА ГРАНИЦЕ ДВУХ СРЕД
(ФОРМУЛЫ ФРЕНЕЛЯ)
ЦЕЛЬ РАБОТЫ: Изучение законов и исследование отражения и прохождения световых электромагнитных волн (ЭМВ) на границе раздела двух сред; анализ амплитудных и энергетических коэффициентов отражения и пропускания ЭМВ на этой границе; освоение методов юстировки оптических систем с использованием лазера.
ПРИНАДЛЕЖНОСТИ: оптическая скамья, маломощный непрерывный лазер, диафрагма, стеклянная плоскопараллельная пластина, укрепленная на лимбе, фотоприемник.
-
Теоретическая часть
Электромагнитная волна, падая на границу раздела двух сред, частично отражается от поверхности раздела и частично преломляется, переходя во вторую среду. Физические явления, имеющие место в этом случае, следует прежде всего охарактеризовать энергетически, вводя понятие коэффициентов отражения и пропускания. Но необходимо исследовать и фазовые соотношения на границе двух сред. Это позволит получить новую информацию об изучаемых физических явлениях.
1.1. Законы отражения и преломления электромагнитных волн
Граничные условия для векторов поля световой волны на границе между двумя диэлектриками при отсутствии свободных зарядов и токов проводимости имеют вид:
где t, n – индексы тангенциальных (касательных к границе раздела) и нормальных компонент векторов соответственно. Пусть на плоскую границу двух диэлектриков с абсолютными (не относительными!) проницаемостями (e1 ; m1) и (e2 ; m2) (магнитную проницаемость пока оставим в общем виде) падает под некоторым углом плоская световая волна (рис.1). Тогда для напряженностей электрического поля в падающей, отраженной и преломленной волнах соответственно имеем:

Рис. 1
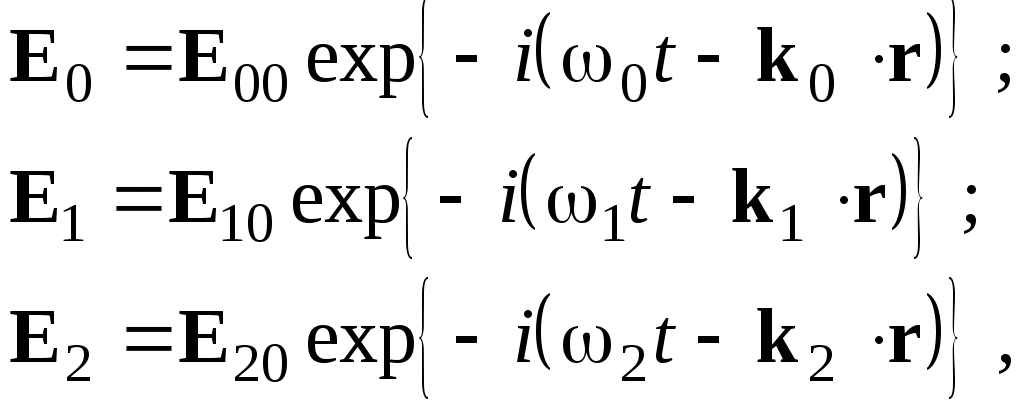 (3)
(3)где
– волновые числа, причем
Законы отражения и преломления света на границе полностью определяются граничными условиями (1) и (2).
Для электрического поля с учетом (3) граничные условия принимают вид:
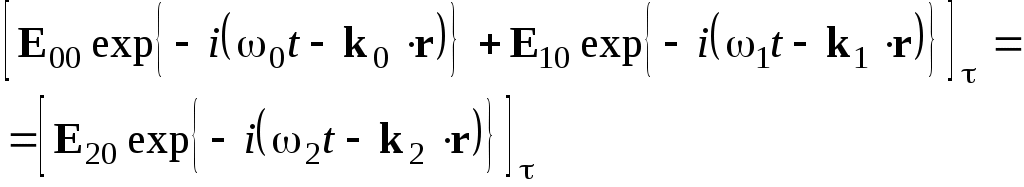 (4)
(4)Отметим, что начало отсчета вектора r (точка 0’ ) совершенно произвольно. Если 0’ лежит не на поверхности раздела, то
При этом в (4):
Равенство (4) будет соблюдаться для произвольных значений r и t только при
Отсюда следует, что частота ЭМВ при отражении и преломлении не меняется
Выберем точку 0’ так, чтобы вектор
Плоскость, в которой лежат волновой вектор k0 и нормаль к поверхности раздела n в точке падения луча, называется плоскостью падения. Из рис.1 видно, что
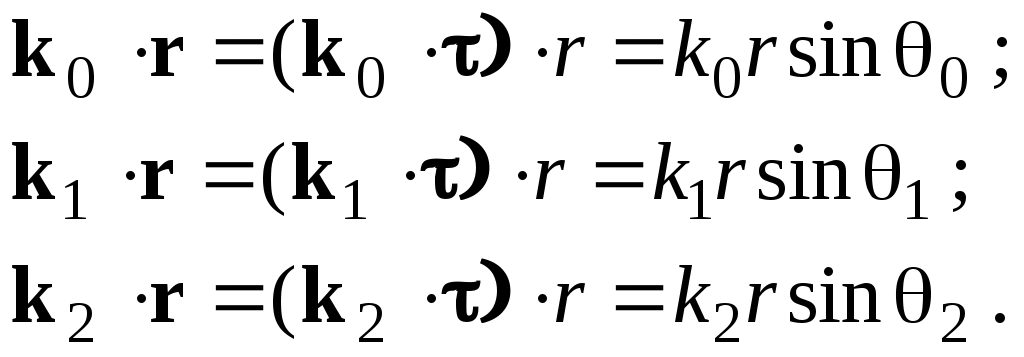 (9)
(9)Тогда с учетом (7) получаем:
или из (3) и (8):
Вспомним, что
– показатели преломления. Из (11) можно сделать следующие выводы:
Введем обозначение
Тогда закон Снеллиуса примет вид:
При
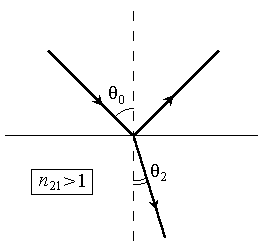
Рис. 2

Рис. 3
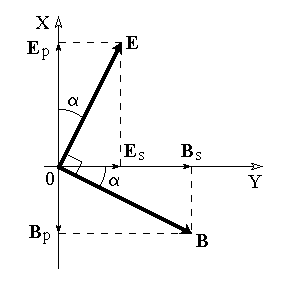 Рис. 4
Рис. 4Вообще говоря, вектор E0 в падающей волне может иметь произвольный азимут a (угол между E и плоскостью падения. Разложим векторы электромагнитного поля на две составляющие: перпендикулярные плоскости падения (будем обозначать их индексом s (или ^) и параллельные плоскости падения (будем обозначать их индексом p (или || )) (рис.4):
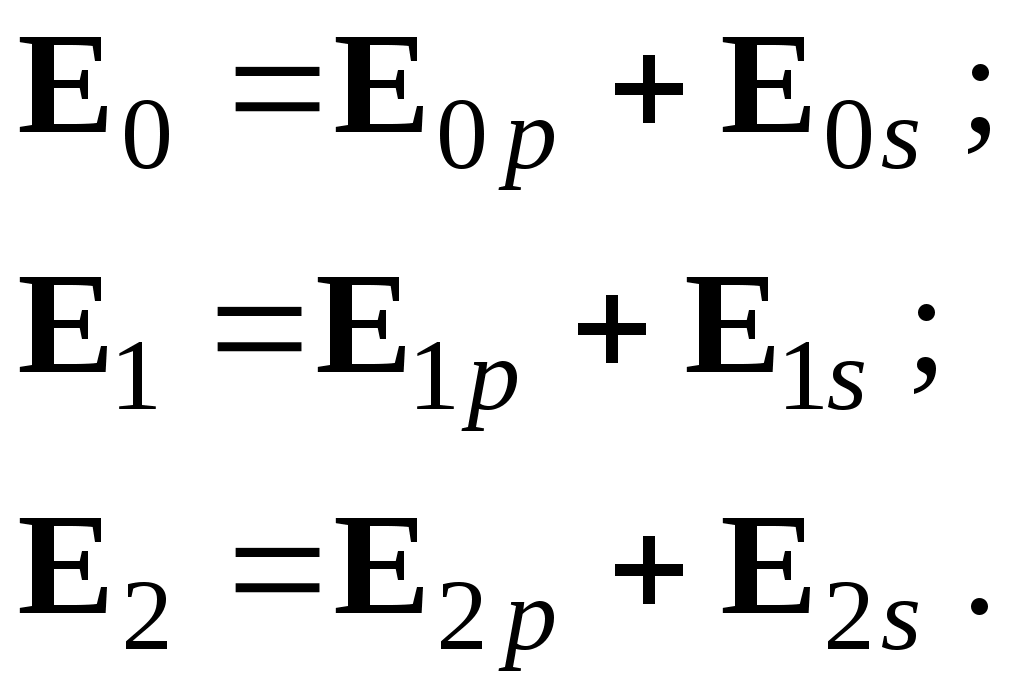 (16)
(16)Видно, что векторы
Т.о., плоскую волну с произвольным азимутом можно разложить на сумму волн, у одной из которых Ep (p – поляризация) лежит в плоскости падения, а у другой