Файл: Практикум волгоград 2014 Печатается по решению редакционноиздательского совета.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 257
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Es (s – поляризация) – перпендикулярна ей. Изучив поведение этих волн на границе с учетом принципа суперпозиции и аддитивности (в данном случае) плотностей потока энергии, получим поведение ЭМВ с произвольным азимутом.
1.2. Отражение и преломление s-поляризованной ЭМВ
Введем единичные векторы в направлении волновых векторов:
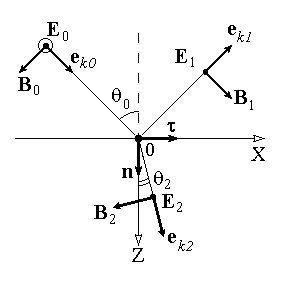 Рис. 5
Рис. 5
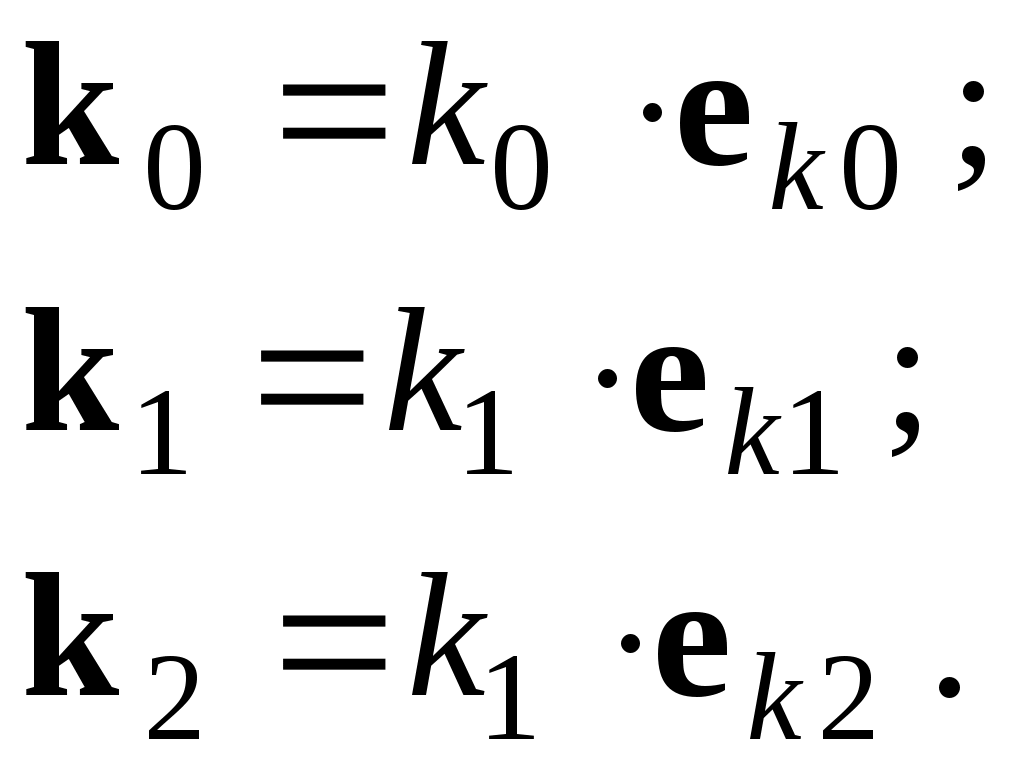 (17)
(17)
Как направлены векторы E1 и E2 заранее не известно. Направим условно их так, как показано на рис.5. Если знак получится отрицательный, значит векторы направлены в противоположную сторону.
Граничные условия для s–поляризации (индексы s опустим):
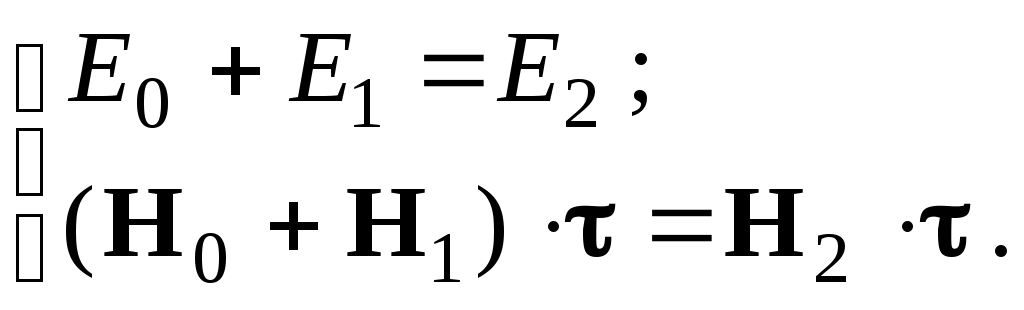 (18) – (19)
(18) – (19)
Обозначим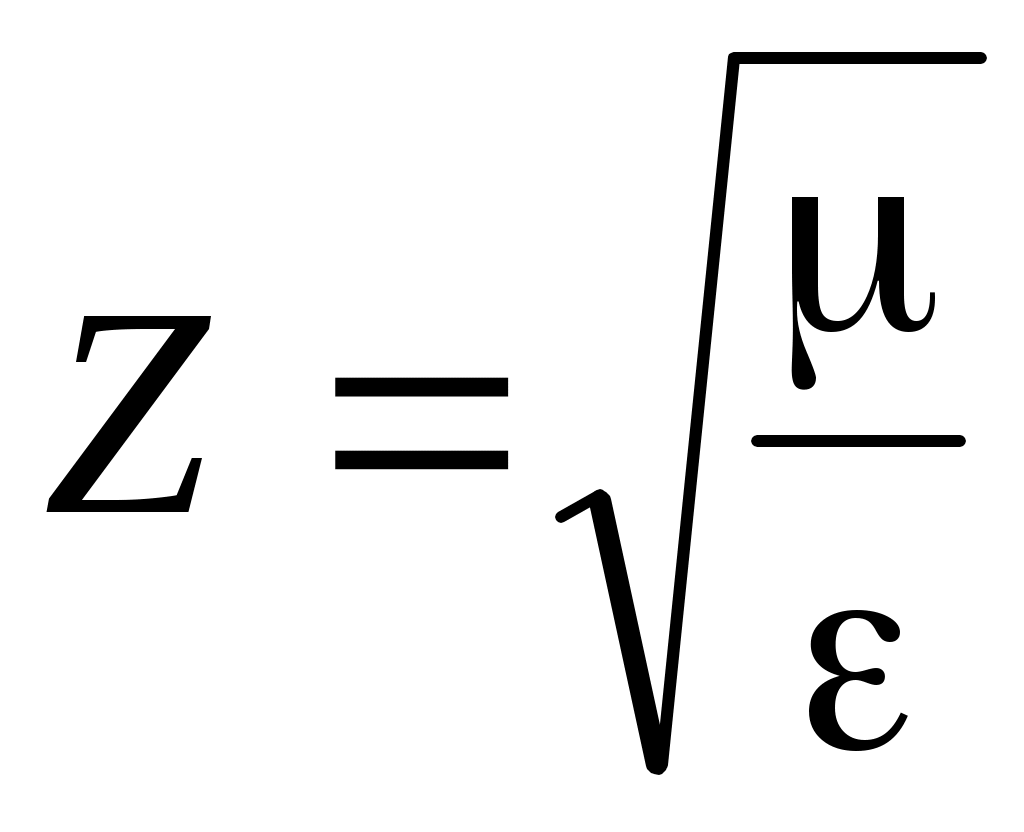 – волновое сопротивление (импеданс) среды. (Для вакуума
– волновое сопротивление (импеданс) среды. (Для вакуума 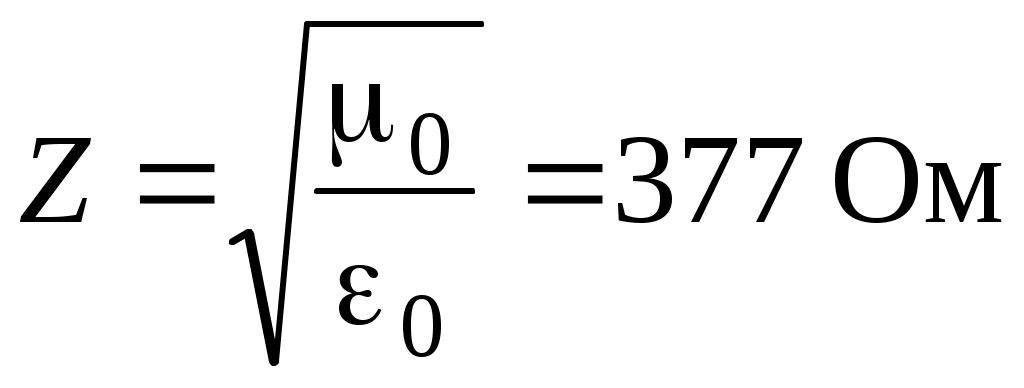 .) В оптике, в отличие от электричества, понятие волнового сопротивления среды практически не используется. Но для удобства записи мы им временно воспользуемся. Тогда
.) В оптике, в отличие от электричества, понятие волнового сопротивления среды практически не используется. Но для удобства записи мы им временно воспользуемся. Тогда
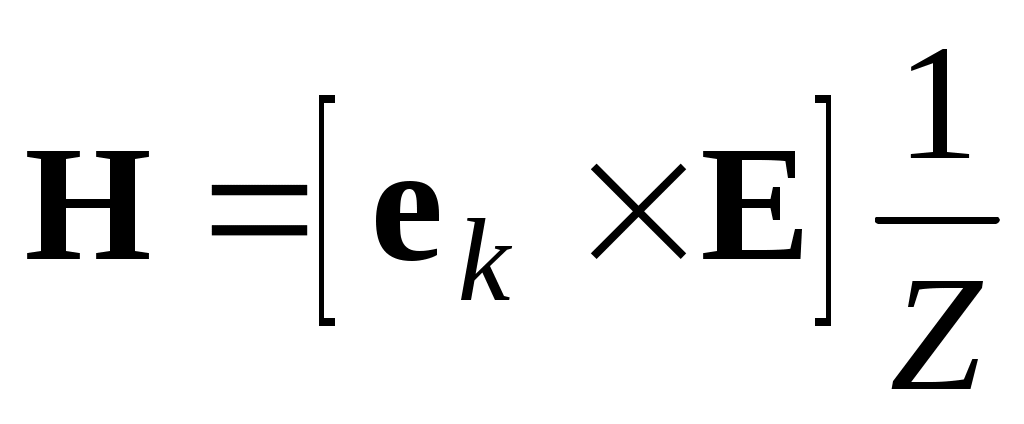 (20)
(20)
Из рис.5 можно найти связь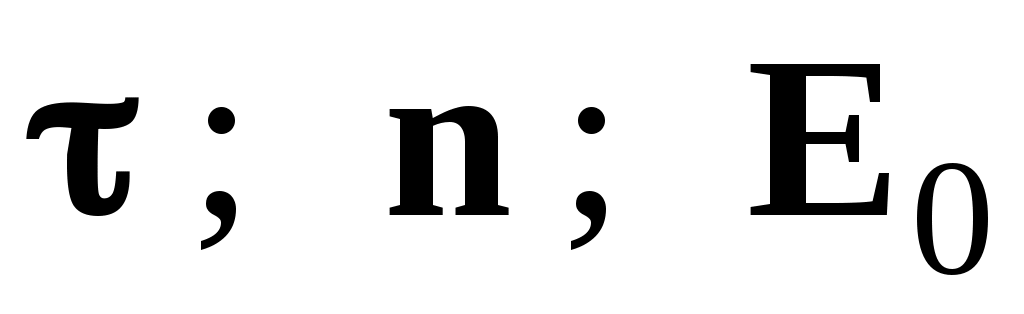 :
:
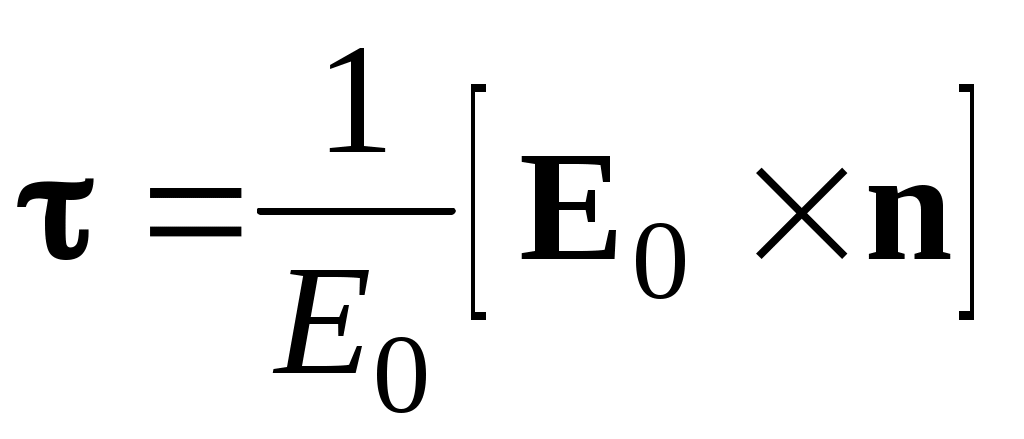 (21)
(21)
Для дальнейшего использования в (19) получим из (20) и (21) скалярное произведение для любой из рассматриваемых волн:
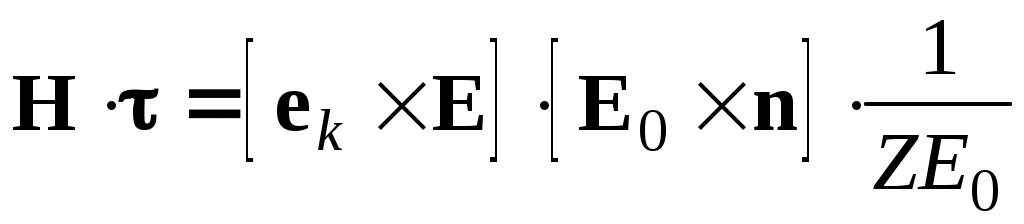 . (22)
. (22)
С учетом известной из векторного анализа формулы
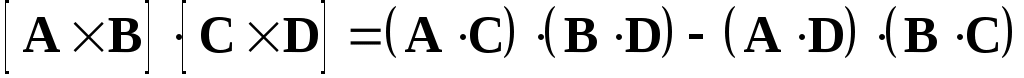 (23)
(23)
получаем: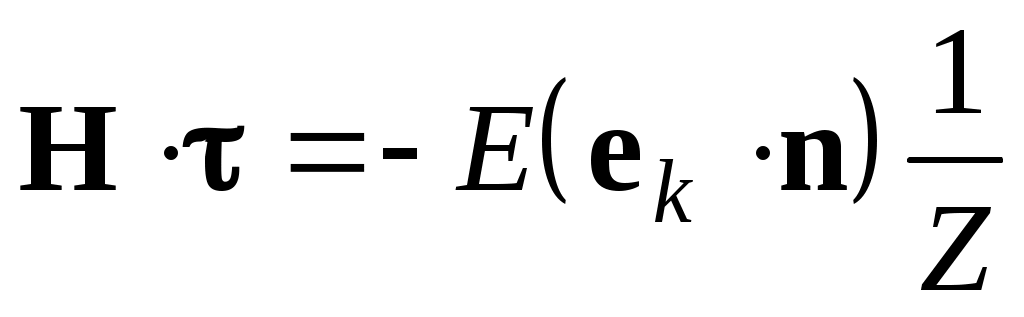 . (24)
. (24)
Тогда из (19) имеем:
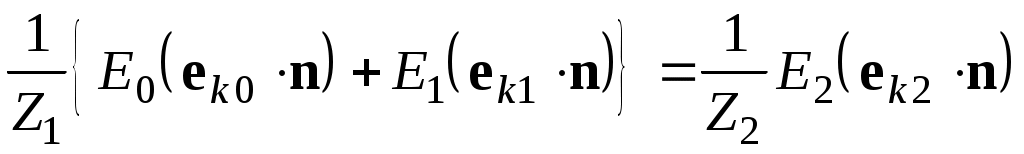 . (25)
. (25)
Соотношения (25) и (18) совместно можно записать в виде:
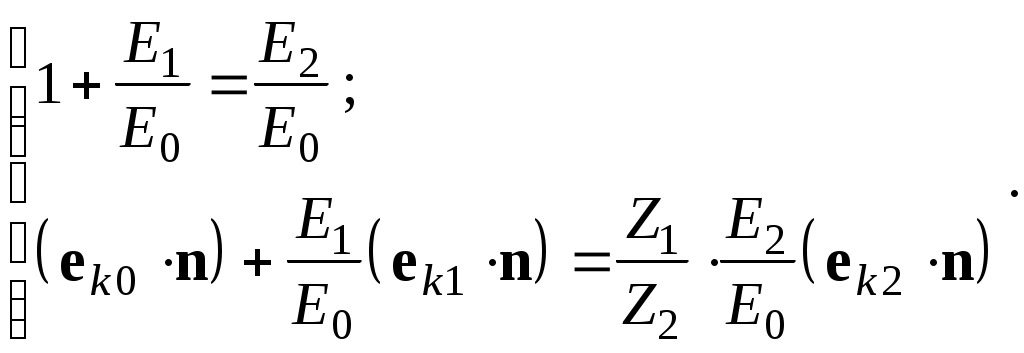
(26)
Обозначим: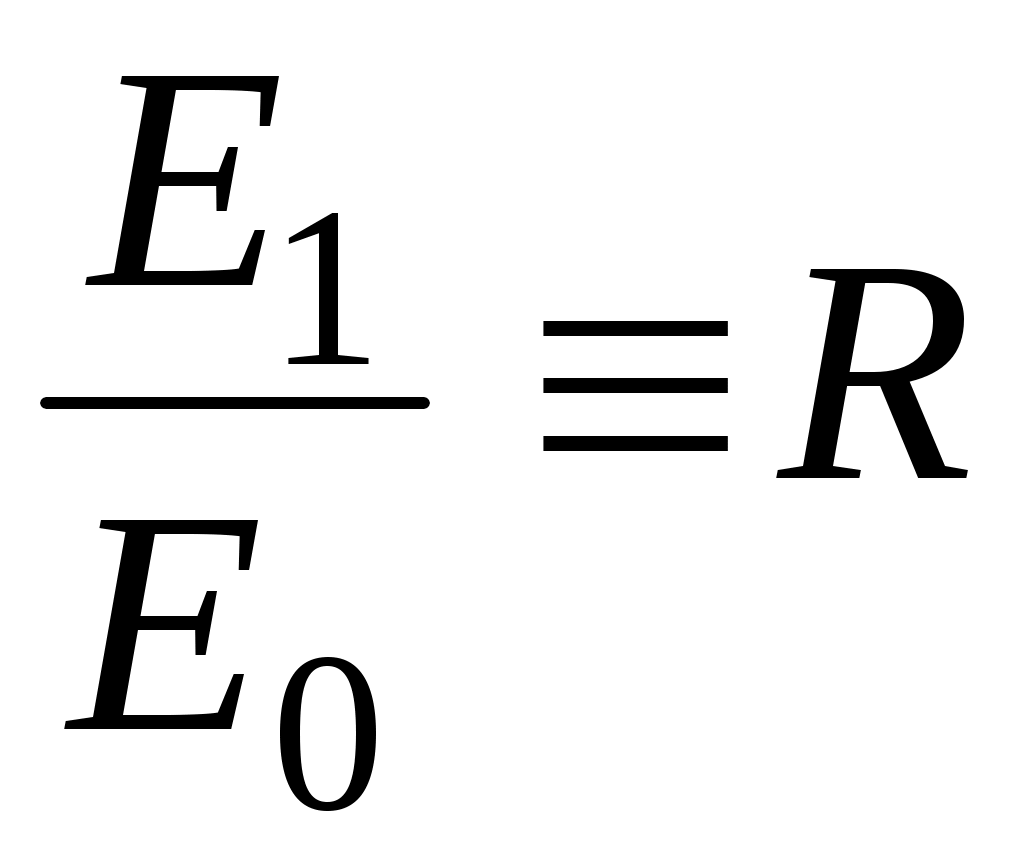 – амплитудный коэффициент отражения; (27)
– амплитудный коэффициент отражения; (27)
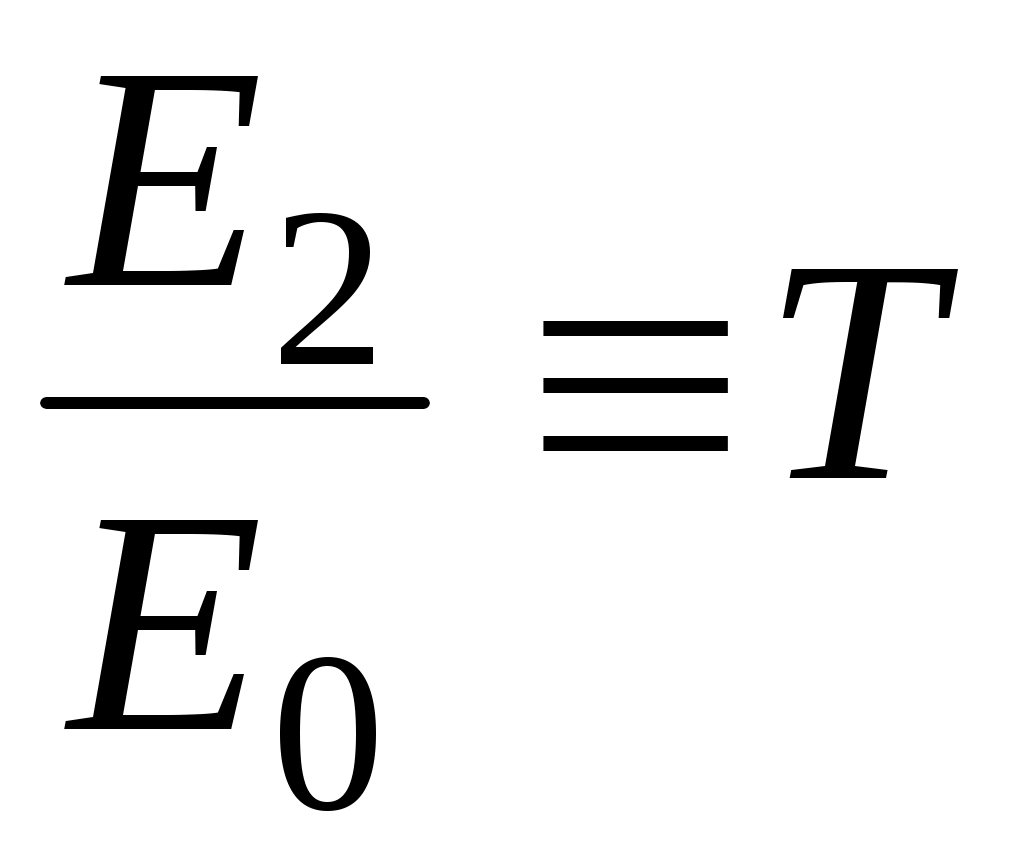 – амплитудный коэффициент пропускания. (28)
– амплитудный коэффициент пропускания. (28)
Учтем, что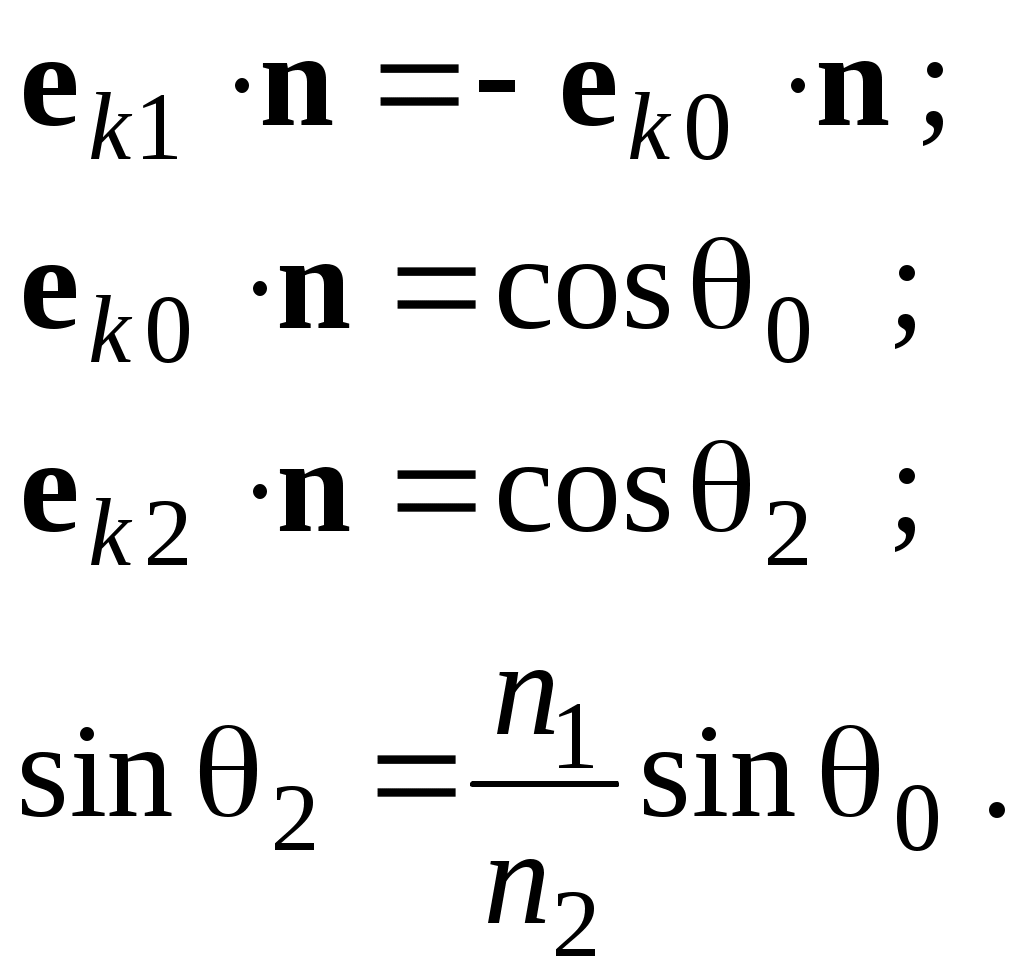 (29)
(29)
При система (26) имеет действительное решение для всех углов q0 . Если
система (26) имеет действительное решение для всех углов q0 . Если 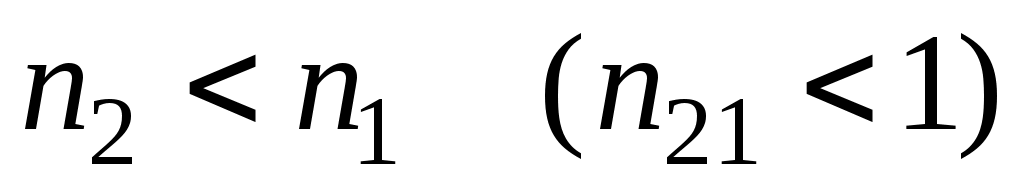 она имеет действительное решение лишь для углов
она имеет действительное решение лишь для углов 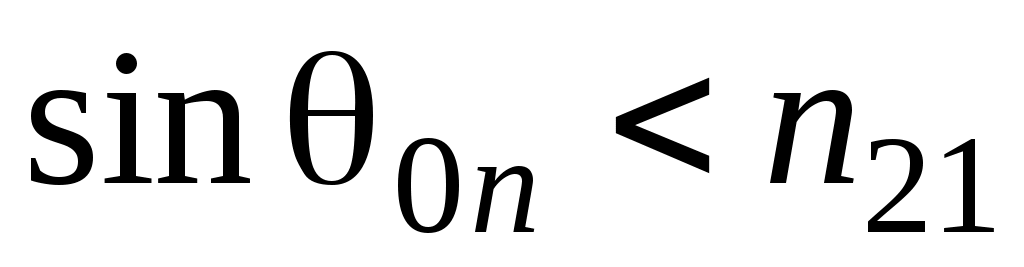 (подробнее этот случай рассмотрим позднее). Тогда имеем обобщенные формулы Френеля для s – поляризации:
(подробнее этот случай рассмотрим позднее). Тогда имеем обобщенные формулы Френеля для s – поляризации:
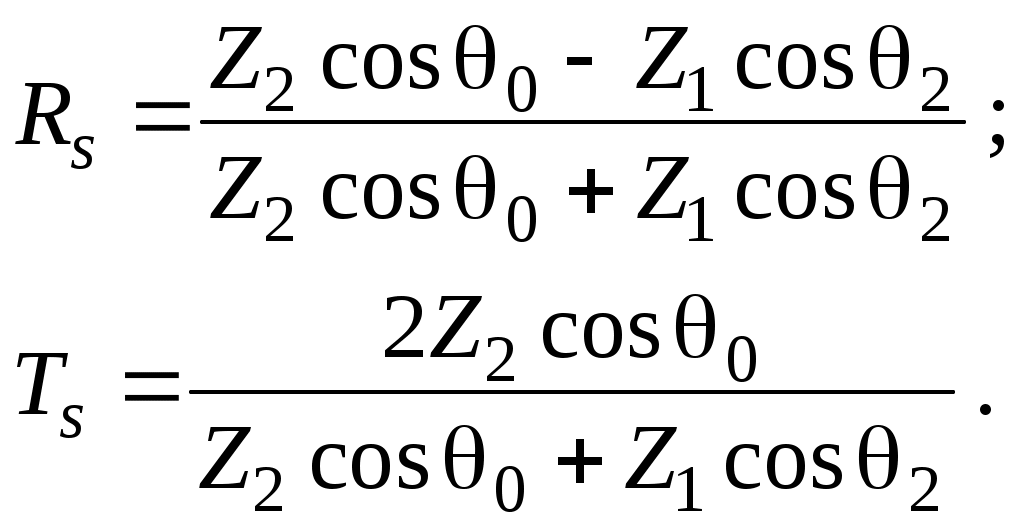 (30) – (31)
(30) – (31)
Для диэлектриков в оптическом диапазоне обычно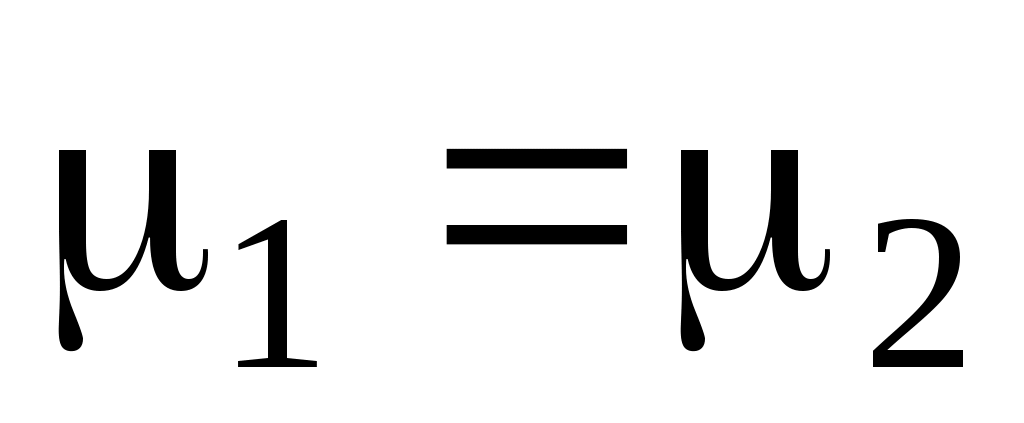 . Тогда из (30) и (31) получим общепринятые формулы Френеля для s – поляризации:
. Тогда из (30) и (31) получим общепринятые формулы Френеля для s – поляризации:
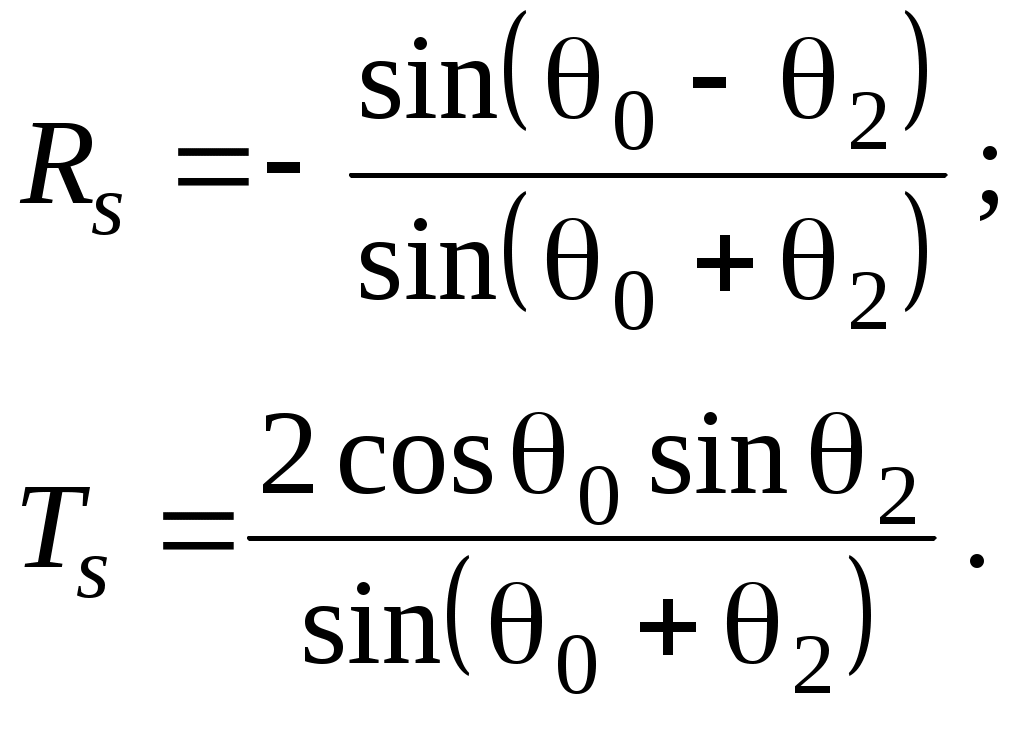 (32) – (33)
(32) – (33)
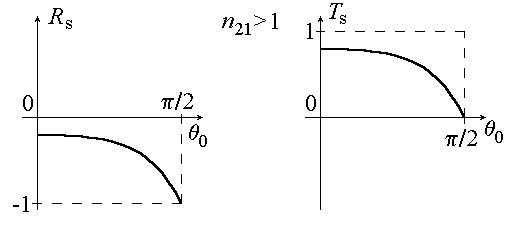 Рис. 6
Рис. 6
Графики зависимостей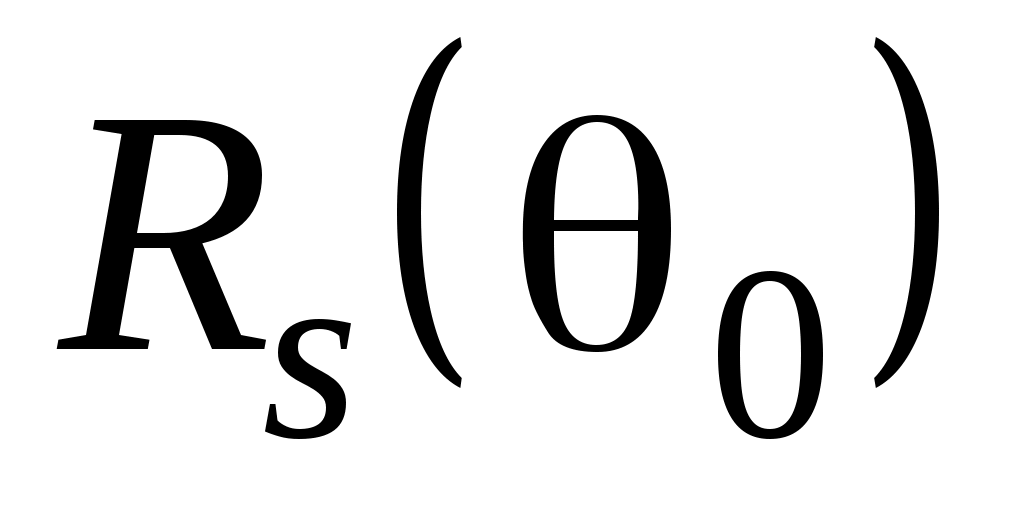 и
и 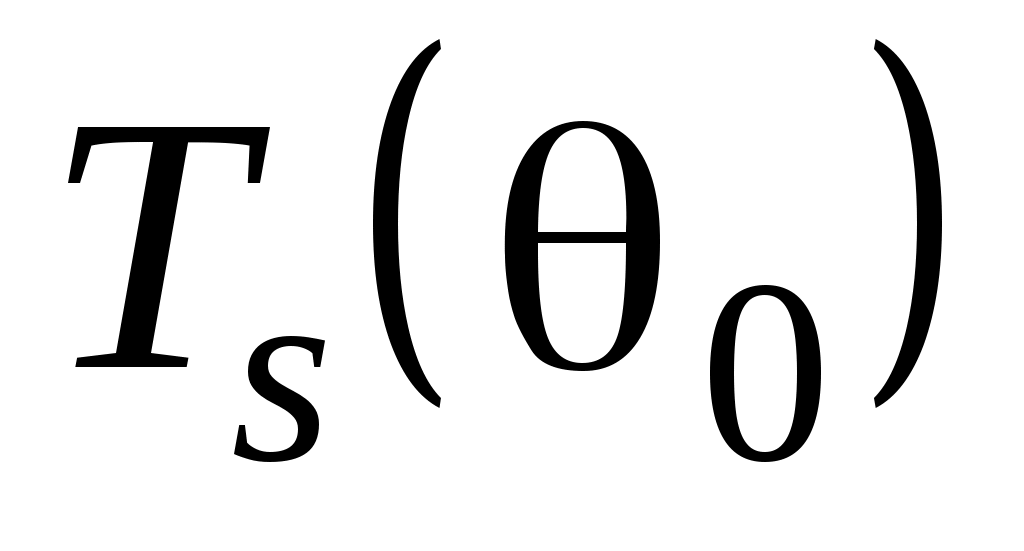 для
для 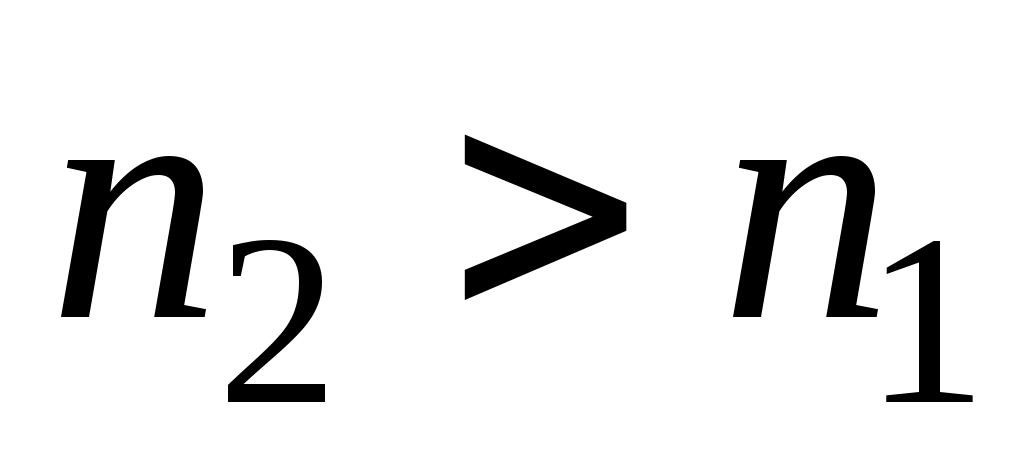 приведены на рис.6.
приведены на рис.6.
При отражении света от диэлектрика с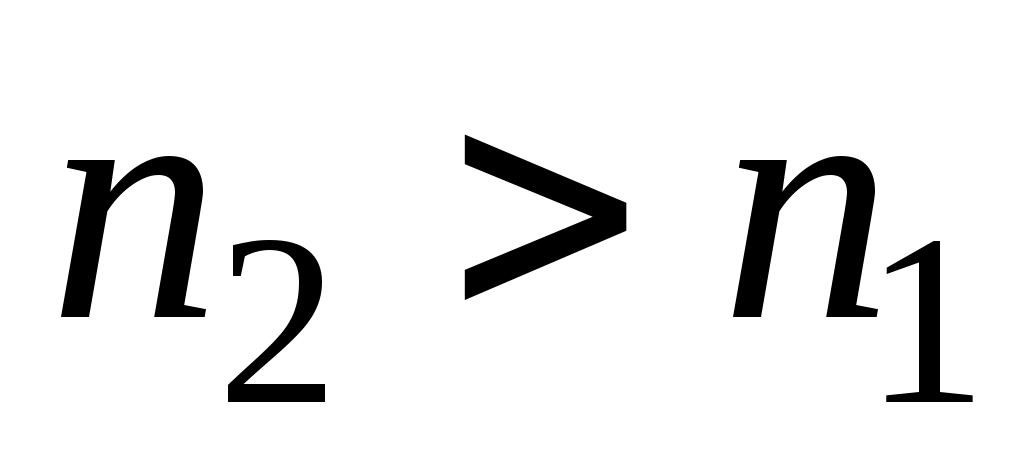 фаза отраженной волны изменяется на p. При преломлении в этом случае изменения фазы нет.
фаза отраженной волны изменяется на p. При преломлении в этом случае изменения фазы нет.
При отражении света от диэлектрика с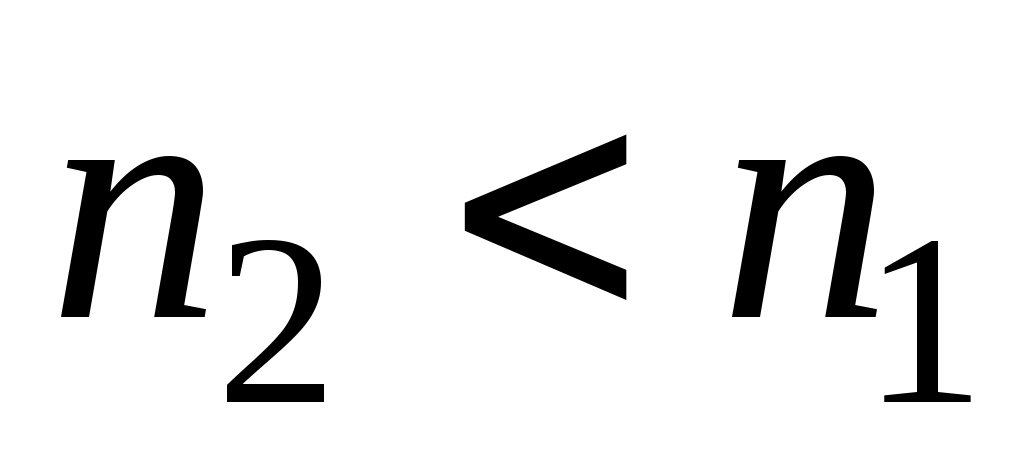 скачка фазы на p не происходит ни для отраженной, ни для преломленной волны.
скачка фазы на p не происходит ни для отраженной, ни для преломленной волны.
1.3. Отражение и преломление p–поляризованной ЭМВ
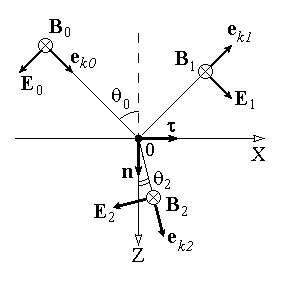 Рис. 7
Рис. 7
Рассмотрение в данном случае проводится аналогично случаю s–поляризации. Для этого учтем, что

(34) – (35)
Отсюда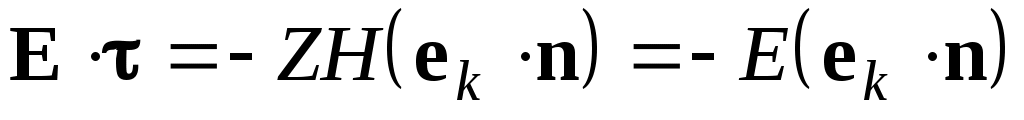 . (36)
. (36)
Граничные условия для p–поляризации принимают вид:
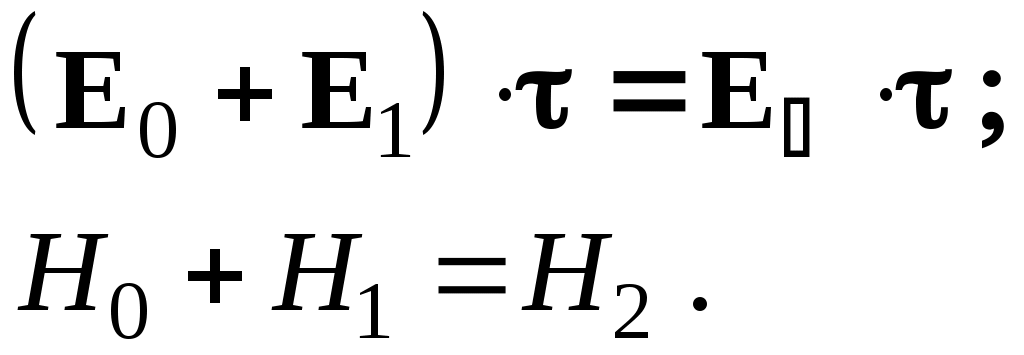 (37) – (38)
(37) – (38)
Подставляя (36) в (37), получаем:
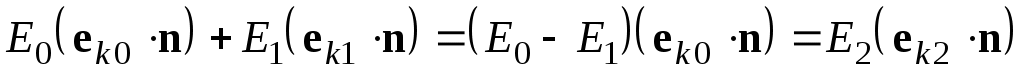 ; (39)
; (39)
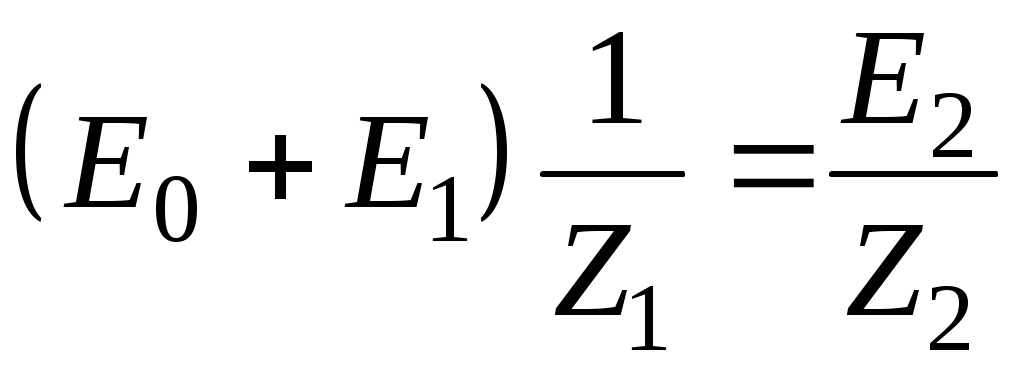 . (40)
. (40)
Для действительных углов преломления получаем обобщенные формулы Френеля для p–поляризации:
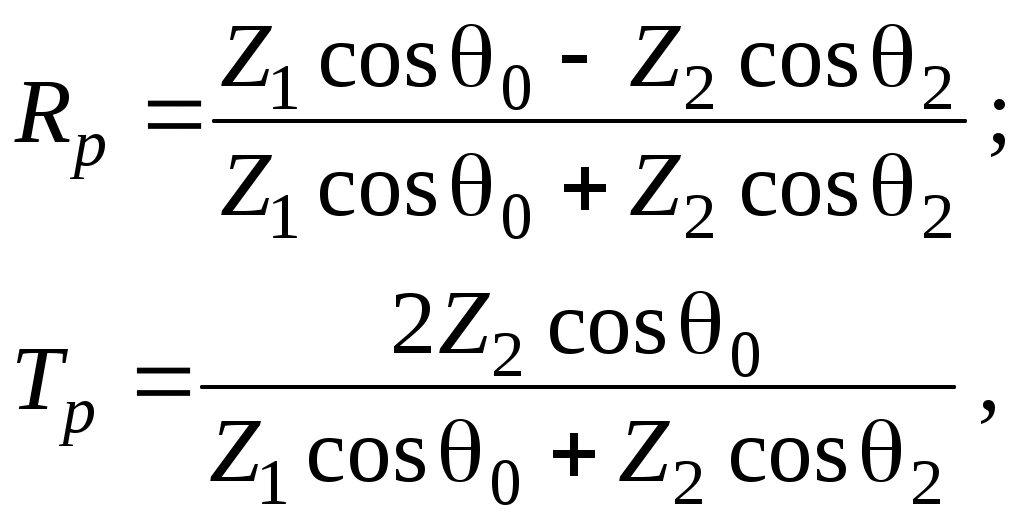 (41) – (42)
(41) – (42)
или для диэлектриков с m1 = m2 :
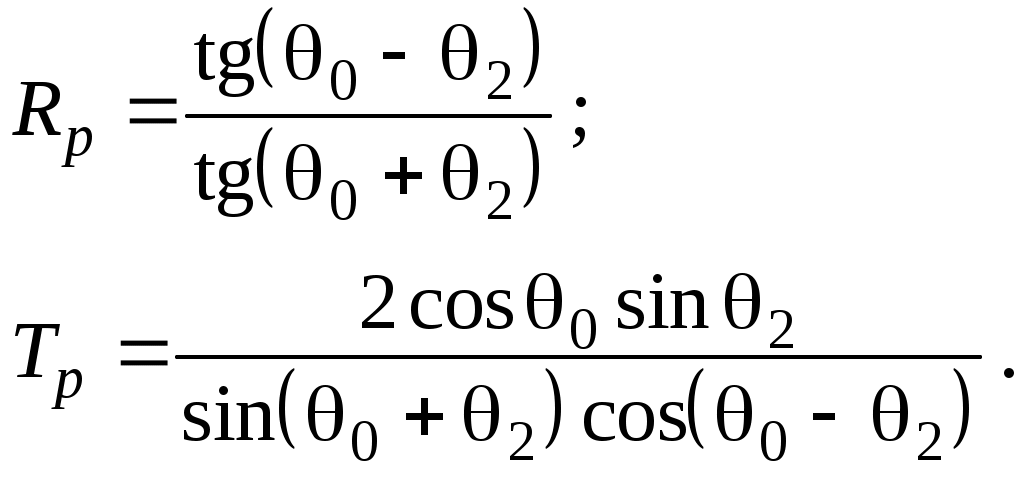 (43) – (44)
(43) – (44)
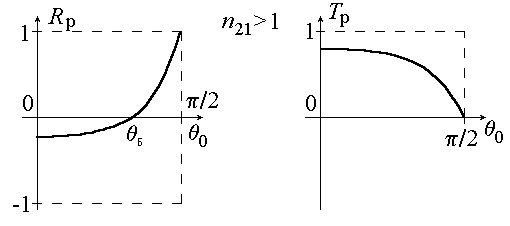
Рис. 8
Графики зависимостей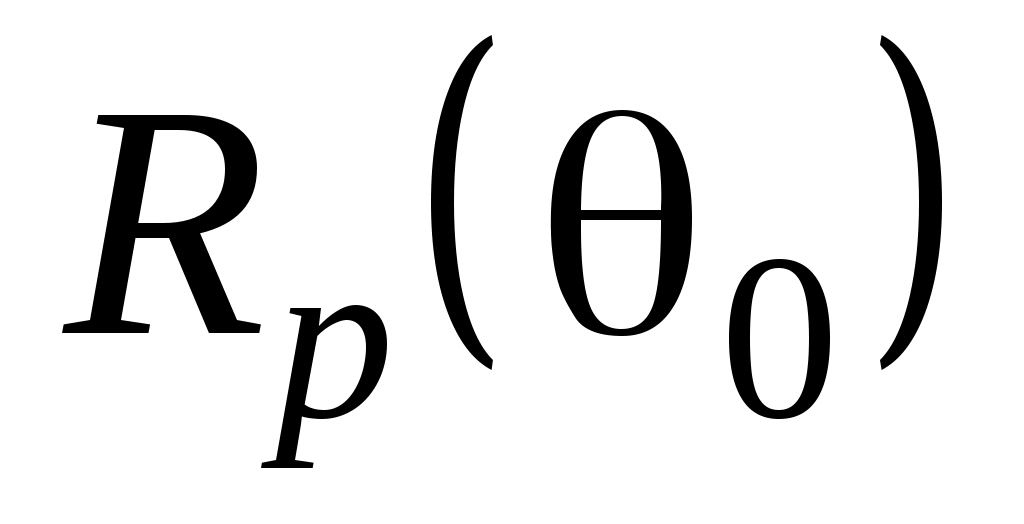 и
и 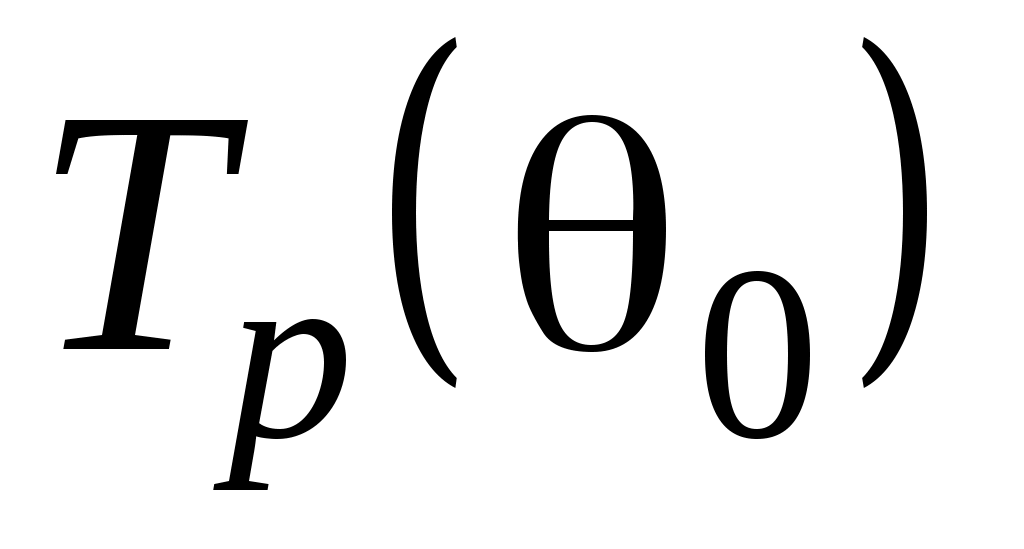 для
для  приведены на рис.8.
приведены на рис.8.
1.4. Явление Брюстера
Из формулы (43) и из графика рис.8 видно, что для p–поляризованной волны при некотором угле падения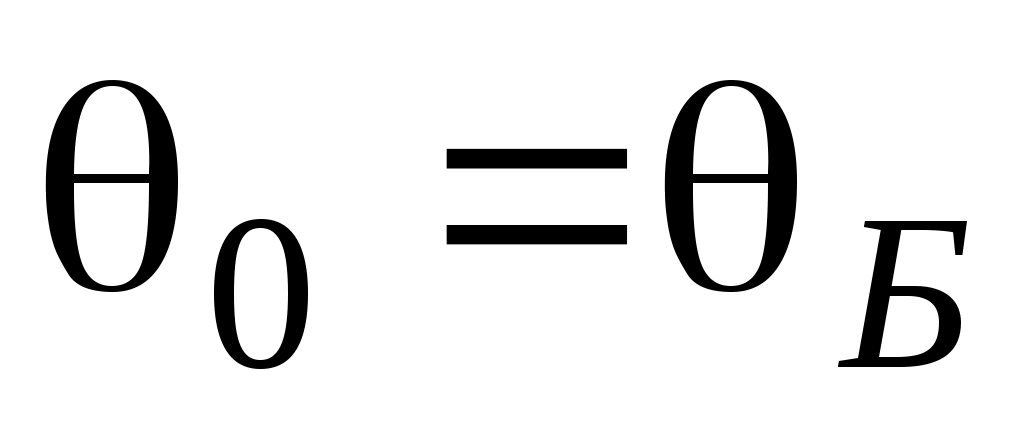 , называемом углом Брюстера, отраженная волна отсутствует, т.е.
, называемом углом Брюстера, отраженная волна отсутствует, т.е. 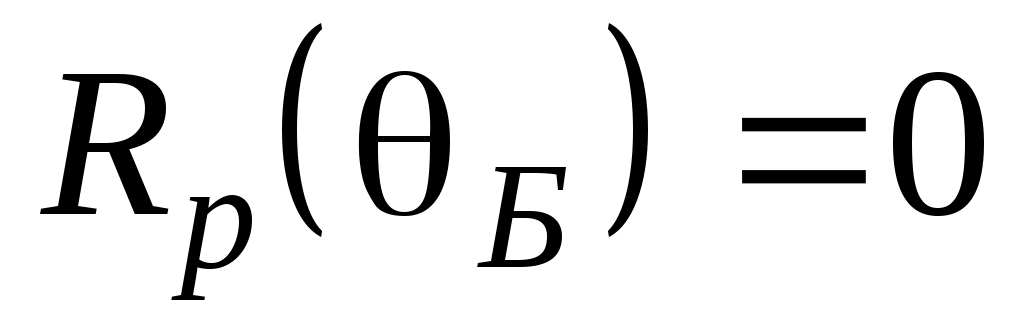 . Это явление называется явлением Брюстера. Для угла Брюстера справедливы следующие соотношения:
. Это явление называется явлением Брюстера. Для угла Брюстера справедливы следующие соотношения:
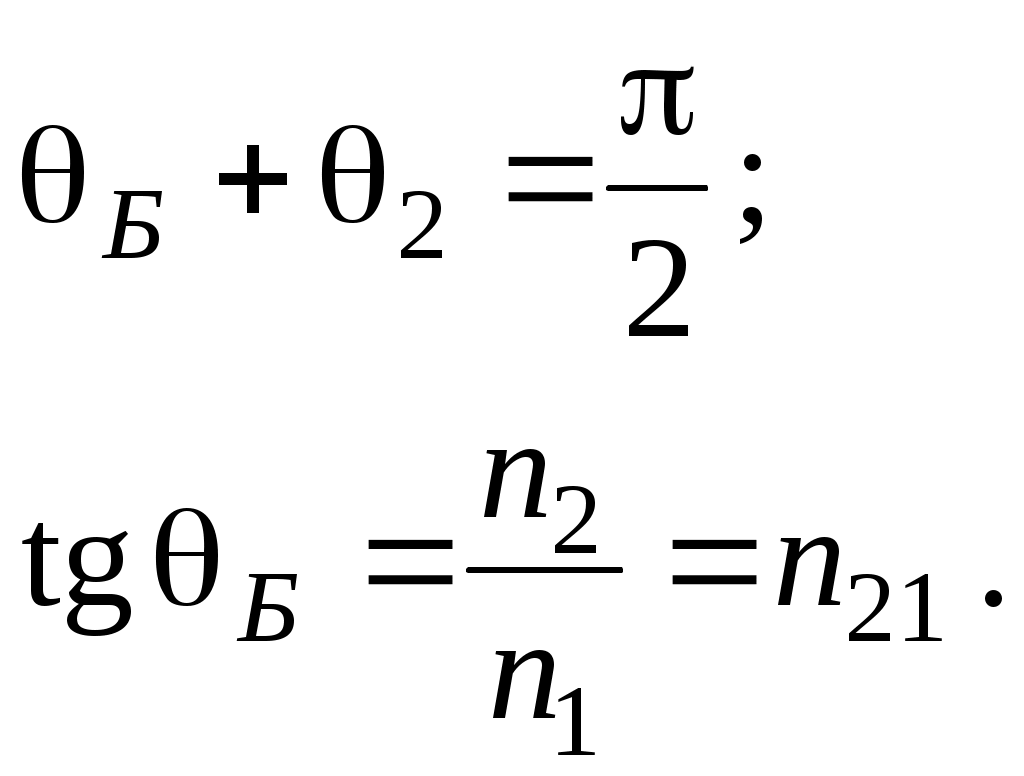 (45)
(45)
При переходе через угол Брюстера фаза колебаний отраженной волны скачком меняется на p.
Заметим, что явлении Брюстера наблюдается тогда, когда направления преломленной и отраженной волны ортогональны. С физической точки зрения это можно объяснить следующим образом. Если связывать наличие отраженной волны с вынужденными колебаниями электронов во второй среде, то в направлении, перпендикулярном преломленной волне, не должна распространяться энергия, т.к. образующийся при этом диполь не излучает в направлении собственных колебаний.
При при падающей волне с произвольным азимутом отражается лишь s – поляризованная компонента. Это является одним из способов получения линейно-поляризованного света.
при падающей волне с произвольным азимутом отражается лишь s – поляризованная компонента. Это является одним из способов получения линейно-поляризованного света.
При нормальном падении света (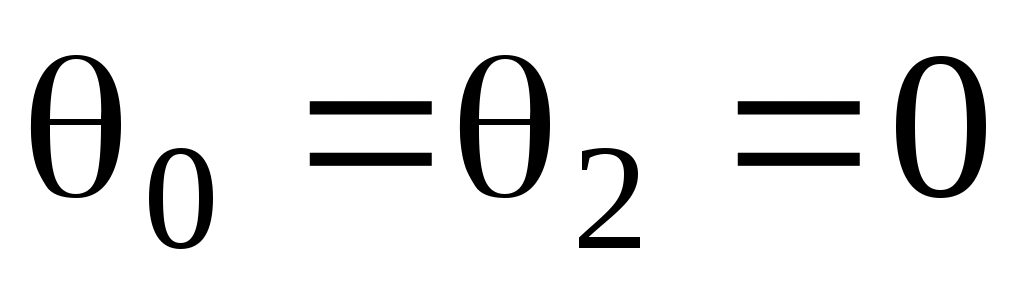 ) понятия s– и p– поляризаций теряют смысл и формулы (30), (31), (41) и (42) дают один и тот же результат (для диэлектрика
) понятия s– и p– поляризаций теряют смысл и формулы (30), (31), (41) и (42) дают один и тот же результат (для диэлектрика 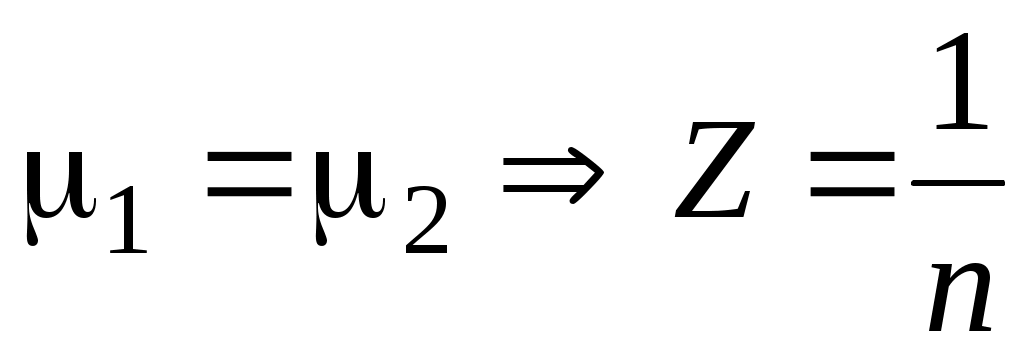 ):
):
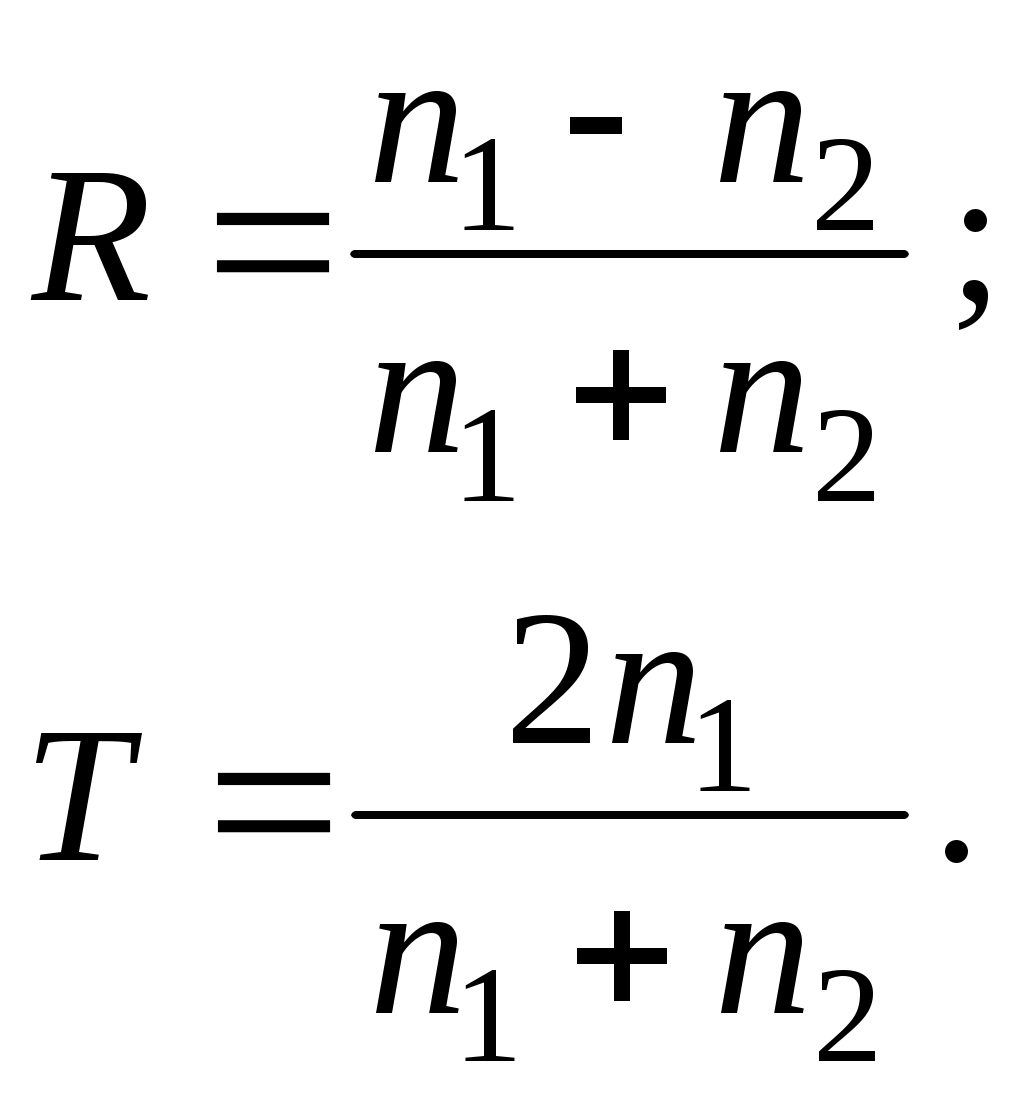 (46) – (47)
(46) – (47)
1.5. Энергетические соотношения при отражении и преломлении света
Энергетическим коэффициентом отражения называется абсолютное значение отношения нормальных компонент векторов Пойнтинга в отраженной и падающих волнах:
называется абсолютное значение отношения нормальных компонент векторов Пойнтинга в отраженной и падающих волнах:
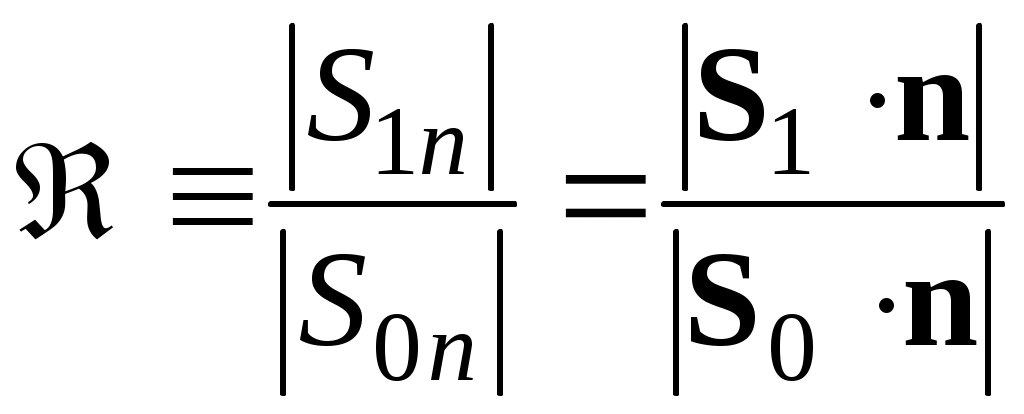 . (48)
. (48)
Энергетический коэффициент пропускания вводится аналогичным образом для преломленной волны:
вводится аналогичным образом для преломленной волны:
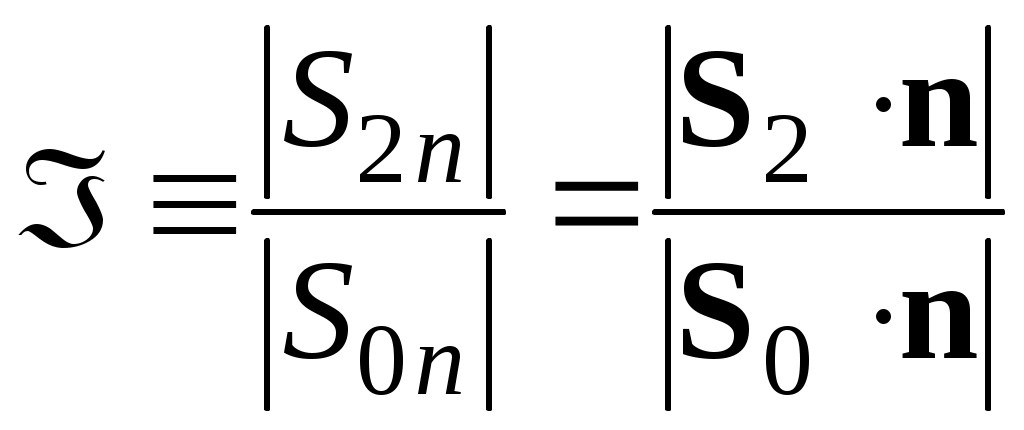 . (49)
. (49)
Т.к. ,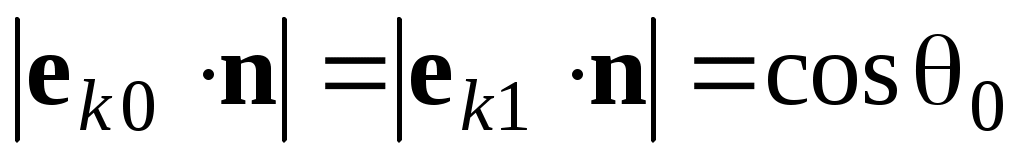 , (50)
, (50)
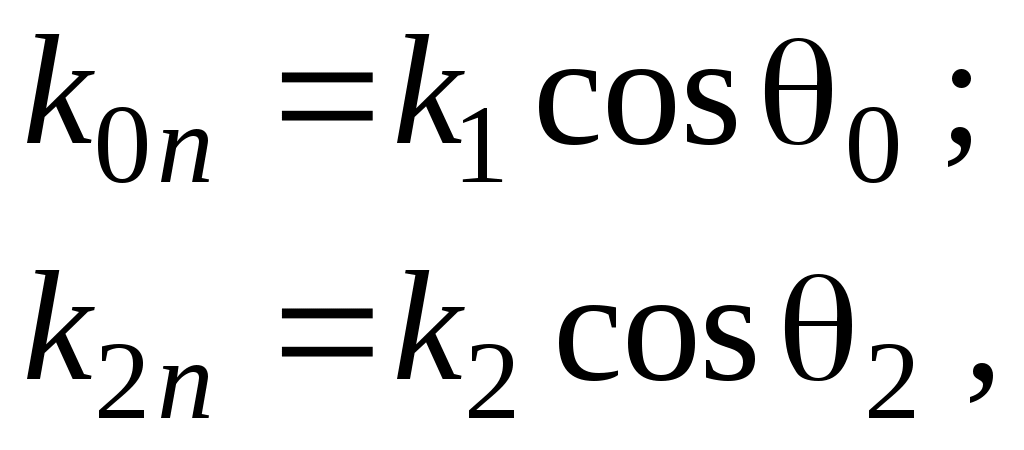 (51)
(51)
то для Â имеем: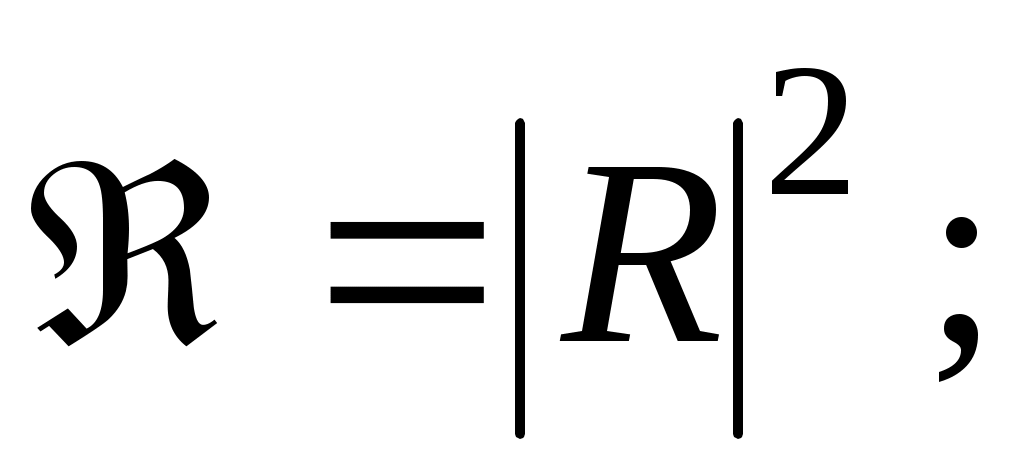 (52)
(52)
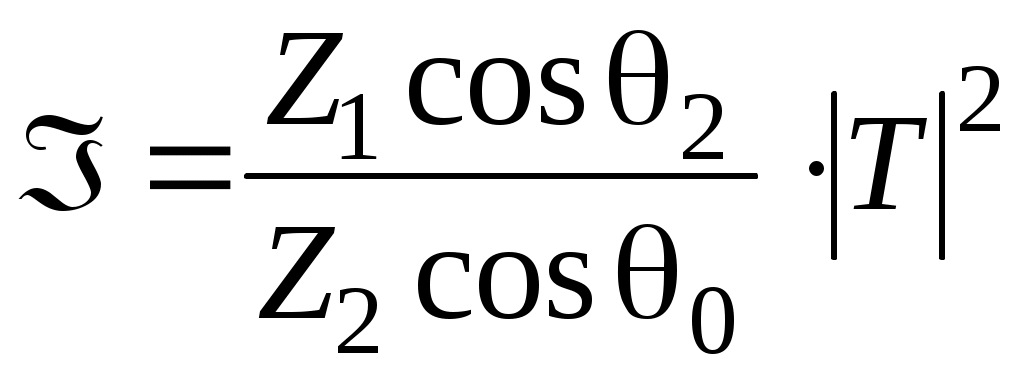 (53)
(53)
или с учетом (30), (31), (41), (42):
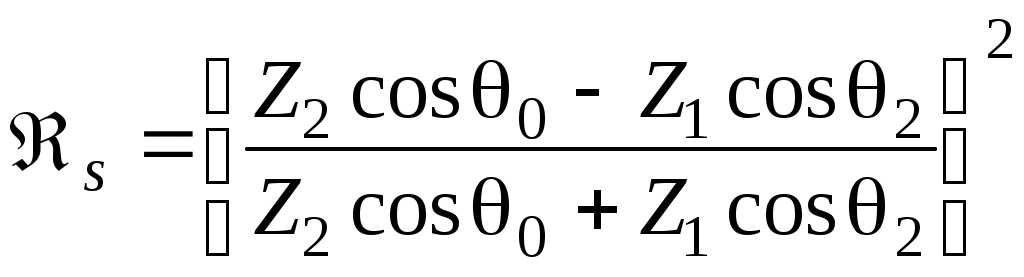 ; (54)
; (54)
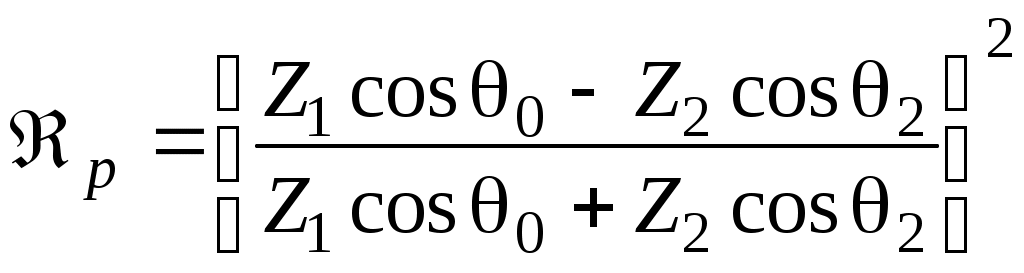 ; (55)
; (55)
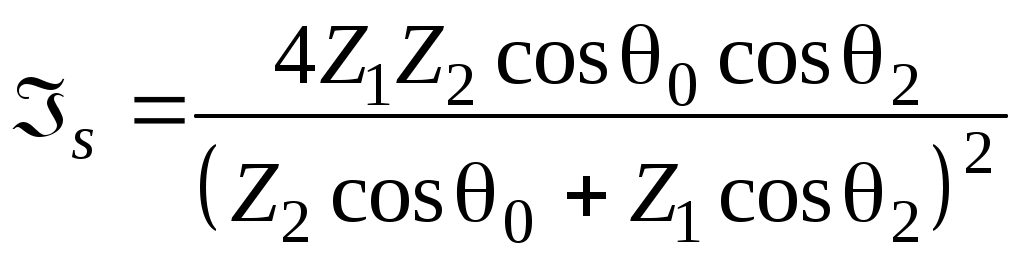 ; (56)
; (56)
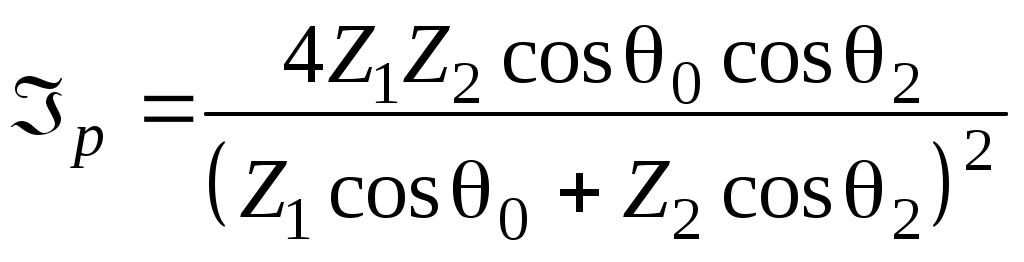 . (57)
. (57)
При q0 = 0 для m1 = m2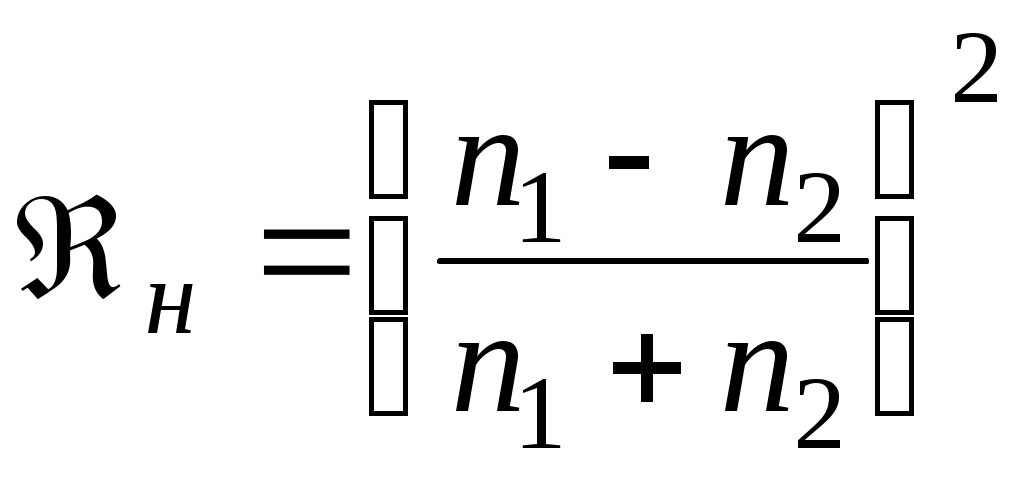 ; (58)
; (58)
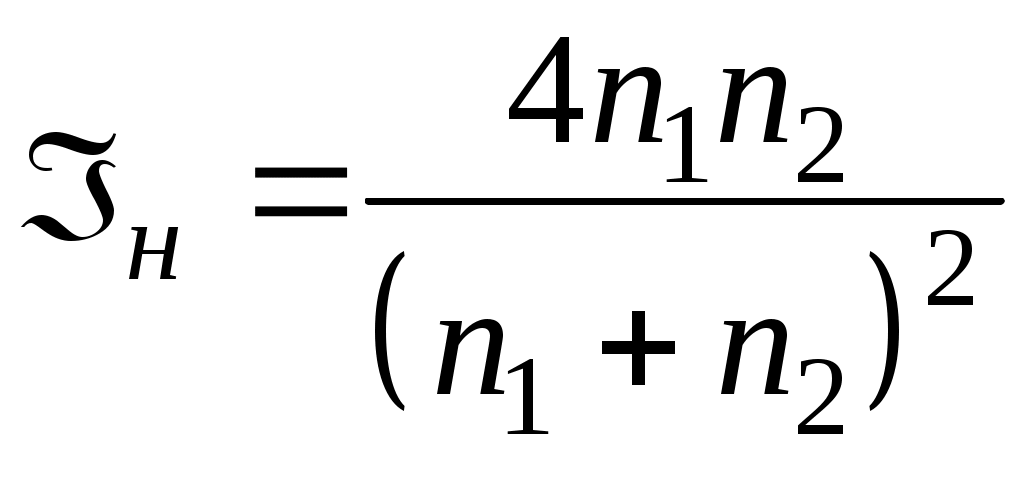 . (59)
. (59)
Прямой проверкой можно показать, что
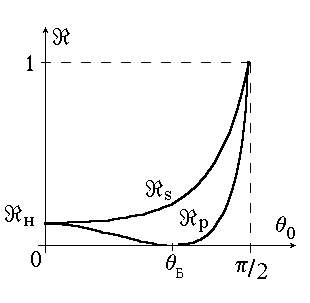 Рис. 9
Рис. 9
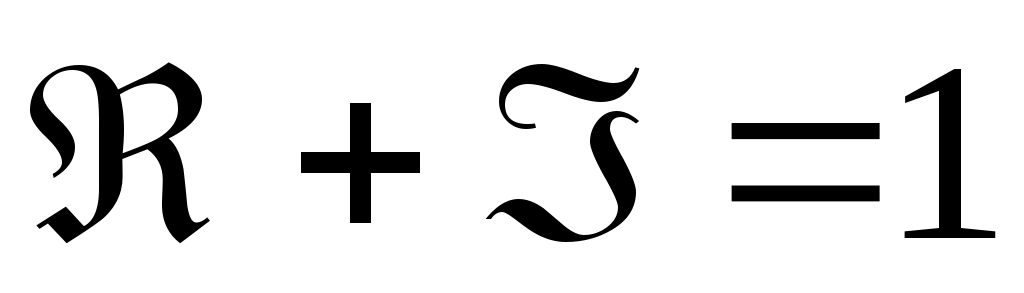 . (60)
. (60)
Это выражает закон сохранения энергии при отражении и преломлении света на границе раздела двух сред. Графики для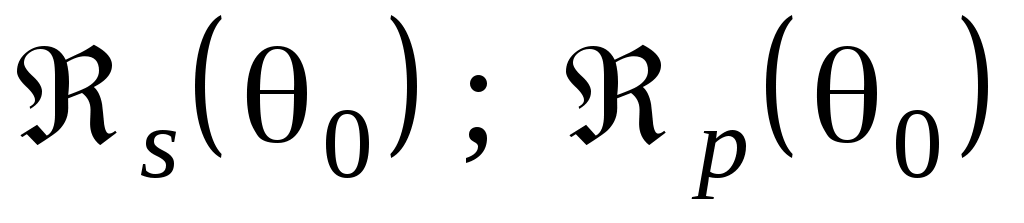 изображены на рис.9.
изображены на рис.9.
2. Описание установки
Лабораторная установка (рис. 10) состоит из маломощного непрерывного лазера ((1) - излучатель, (2) – источник питания лазера), стеклянной плоскопараллельной пластины (3) с показателем преломления n=1.5, укрепленной на лимбе, имеющем градусную меру, фотоприемника (4) с цифровым индикатором и блоком питания (5). Показания цифрового индикатора фотоприемника (фототок) пропорциональны интенсивности света, падающего на фотоприемник. Излучение лазера линейно поляризовано. Все оптические элементы размещены на оптической скамье (6).
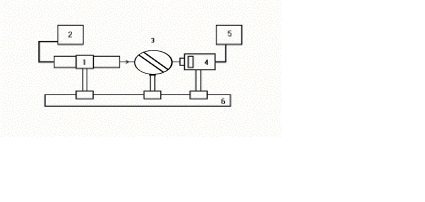
Рис.10. Схема лабораторной установки
3. Порядок выполнения работы
3.1. Установить оптические элементы, входящие в состав установки, на скамью. Проверить с помощью преподавателя правильное соединение элементов электрической части установки.
ВНИМАНИЕ!
В установке используется высокое напряжение и лазерное излучение. Приборы включают только инженер или преподаватель!
3.2. После включения приборов убрать стойку с пластиной, съюстировать оптические элементы так, чтобы луч, пройдя все элементы, попадал на фотоприемник (по максимуму фототока). Измерить фототок, соответствующий интенсивности падающей на пластину световой волны. Установить стойку с пластиной на место. Повторить юстировку.
3.3. Перекрыв лазерное излучение возле самого лазера, измерить темновой ток. В дальнейшем из показаний фотоприемника необходимо вычитать это значение.
3.4. Выставить плоскость поляризации излучения лазера перпендикулярно плоскости падения на стеклянную пластину. При необходимости повторить юстировку.
3.5. Снять зависимость фототока от угла падения света на пластину в диапазоне углов от 0 до 80 градусов с шагом 5 градусов. Угол падения устанавливается поворотом лимба. При изменении угла падения на каждом шаге необходимо подъюстировать фотоэлемент (по максимуму фототока). Измерения повторить не менее трёх раз.
1.2. Отражение и преломление s-поляризованной ЭМВ
Введем единичные векторы в направлении волновых векторов:
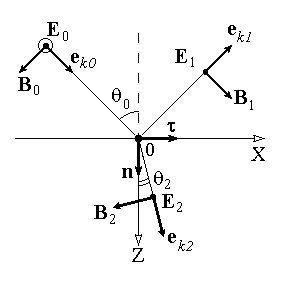 Рис. 5
Рис. 5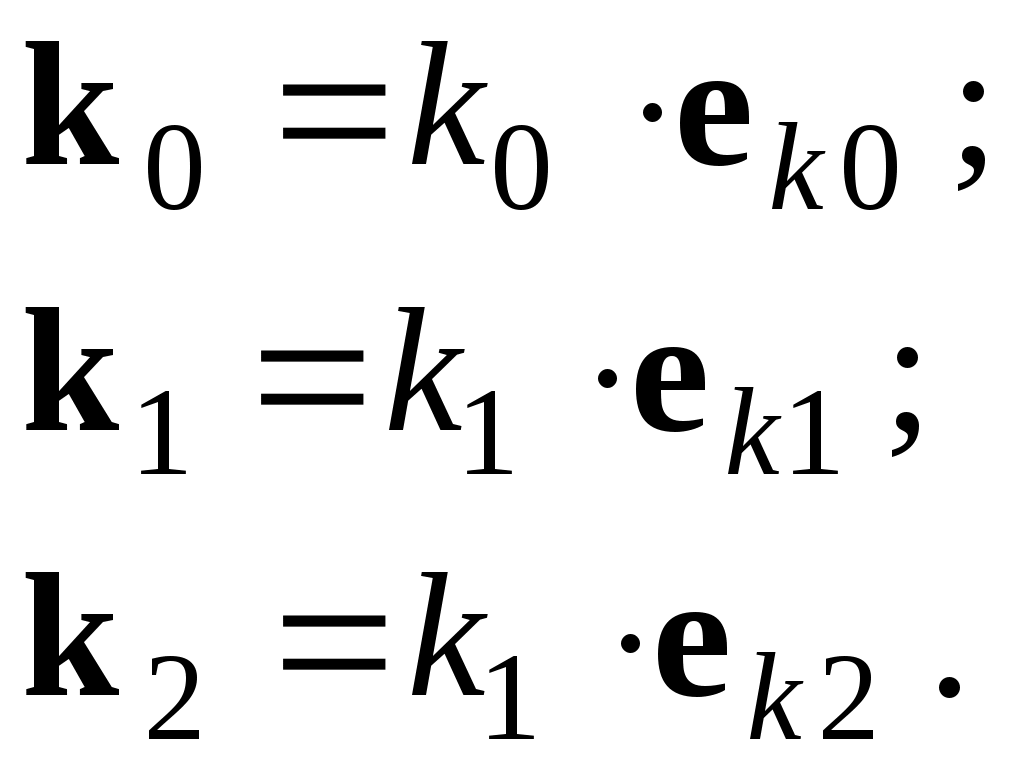 (17)
(17)Как направлены векторы E1 и E2 заранее не известно. Направим условно их так, как показано на рис.5. Если знак получится отрицательный, значит векторы направлены в противоположную сторону.
Граничные условия для s–поляризации (индексы s опустим):
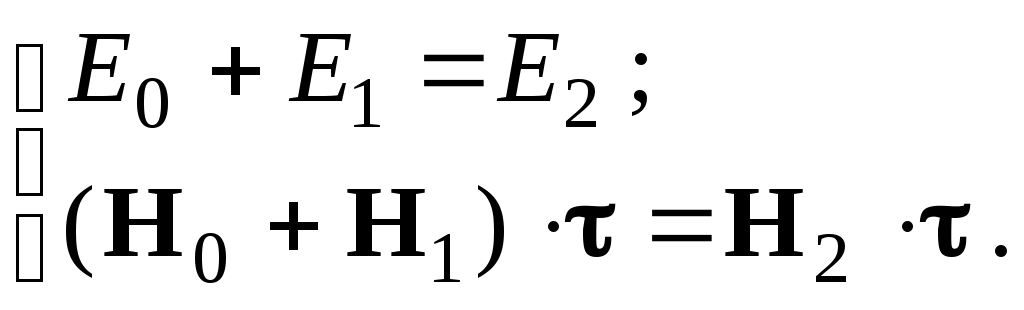 (18) – (19)
(18) – (19)Обозначим
Из рис.5 можно найти связь
Для дальнейшего использования в (19) получим из (20) и (21) скалярное произведение для любой из рассматриваемых волн:
С учетом известной из векторного анализа формулы
получаем:
Тогда из (19) имеем:
Соотношения (25) и (18) совместно можно записать в виде:
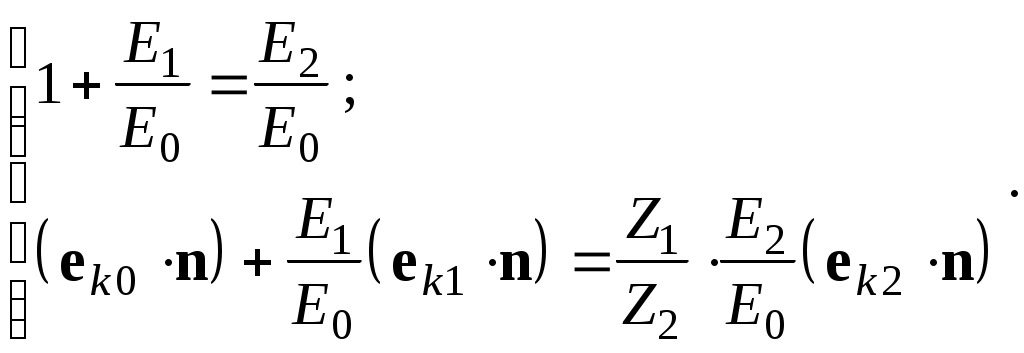
(26)
Обозначим:
Учтем, что
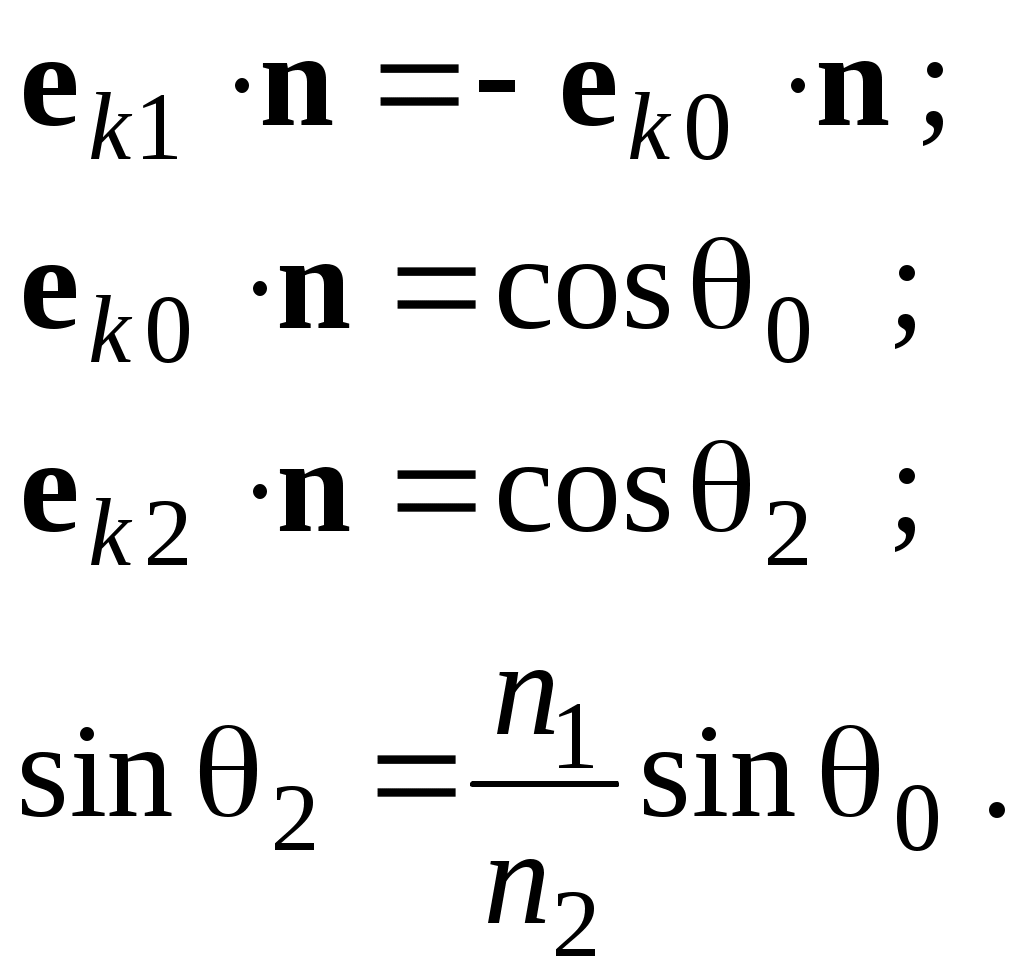 (29)
(29)При
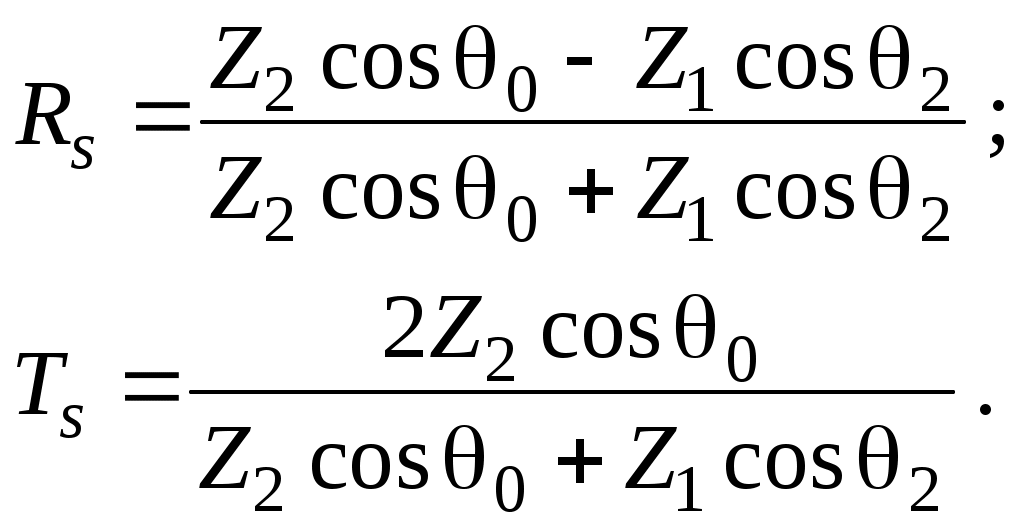 (30) – (31)
(30) – (31)Для диэлектриков в оптическом диапазоне обычно
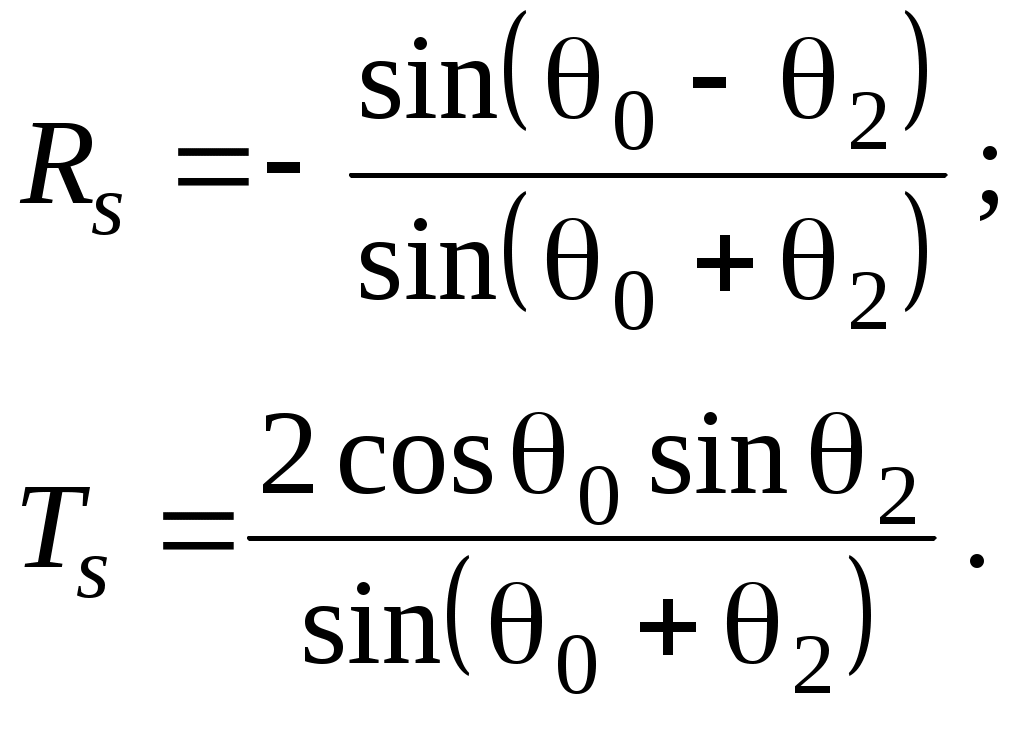 (32) – (33)
(32) – (33)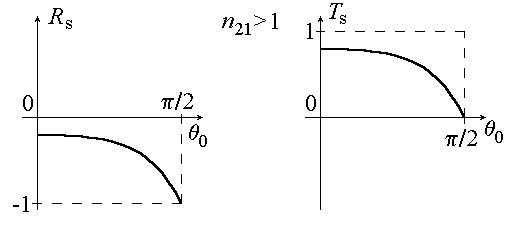 Рис. 6
Рис. 6Графики зависимостей
При отражении света от диэлектрика с
При отражении света от диэлектрика с
1.3. Отражение и преломление p–поляризованной ЭМВ
 Рис. 7
Рис. 7Рассмотрение в данном случае проводится аналогично случаю s–поляризации. Для этого учтем, что

(34) – (35)
Отсюда
Граничные условия для p–поляризации принимают вид:
Подставляя (36) в (37), получаем:
Для действительных углов преломления получаем обобщенные формулы Френеля для p–поляризации:
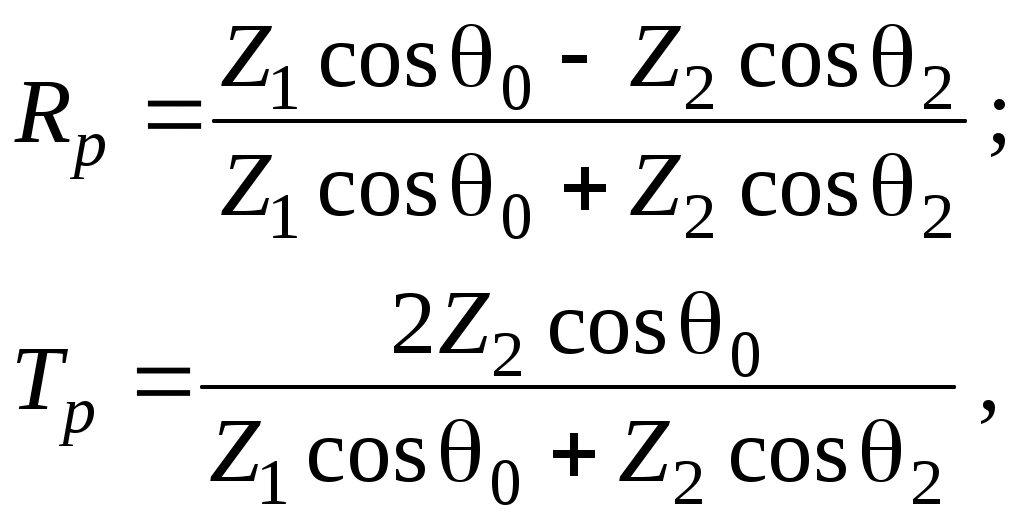 (41) – (42)
(41) – (42)или для диэлектриков с m1 = m2 :
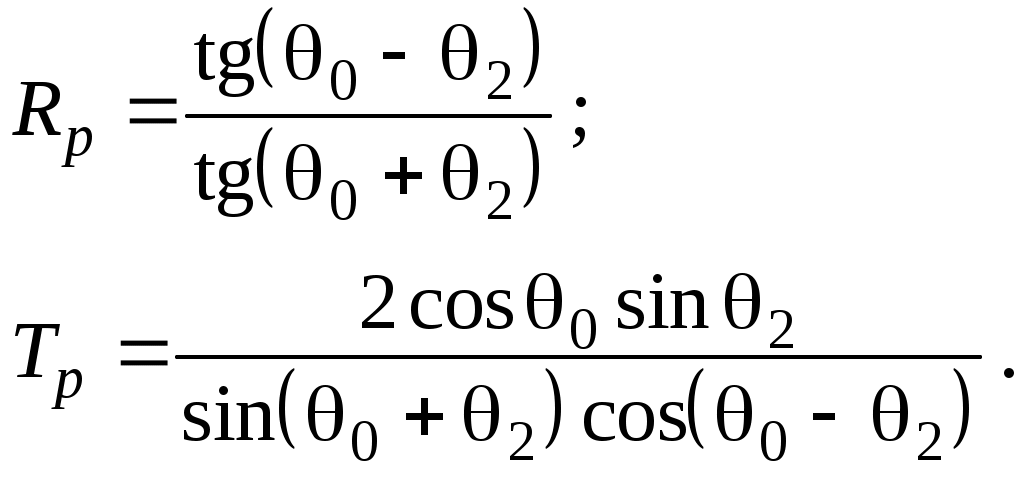 (43) – (44)
(43) – (44)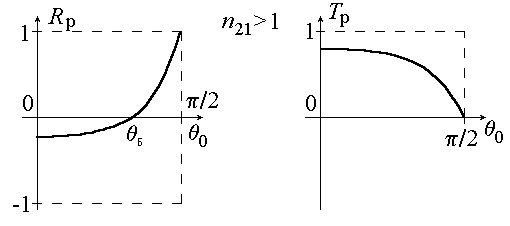
Рис. 8
Графики зависимостей
1.4. Явление Брюстера
Из формулы (43) и из графика рис.8 видно, что для p–поляризованной волны при некотором угле падения
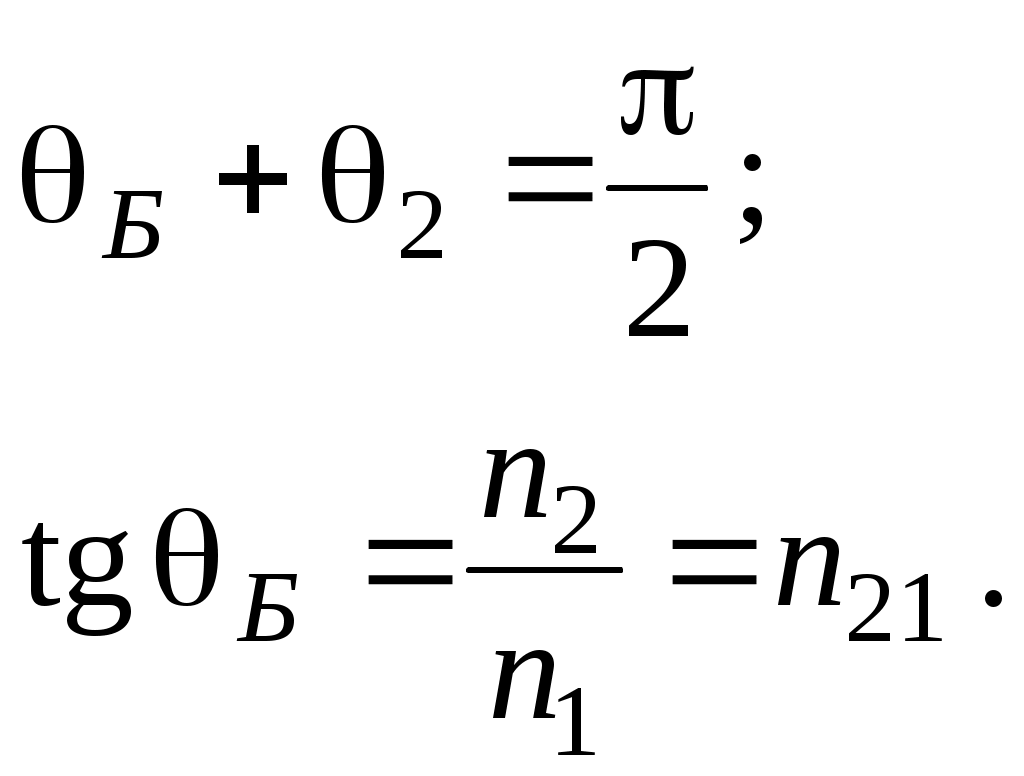 (45)
(45)При переходе через угол Брюстера фаза колебаний отраженной волны скачком меняется на p.
Заметим, что явлении Брюстера наблюдается тогда, когда направления преломленной и отраженной волны ортогональны. С физической точки зрения это можно объяснить следующим образом. Если связывать наличие отраженной волны с вынужденными колебаниями электронов во второй среде, то в направлении, перпендикулярном преломленной волне, не должна распространяться энергия, т.к. образующийся при этом диполь не излучает в направлении собственных колебаний.
При
При нормальном падении света (
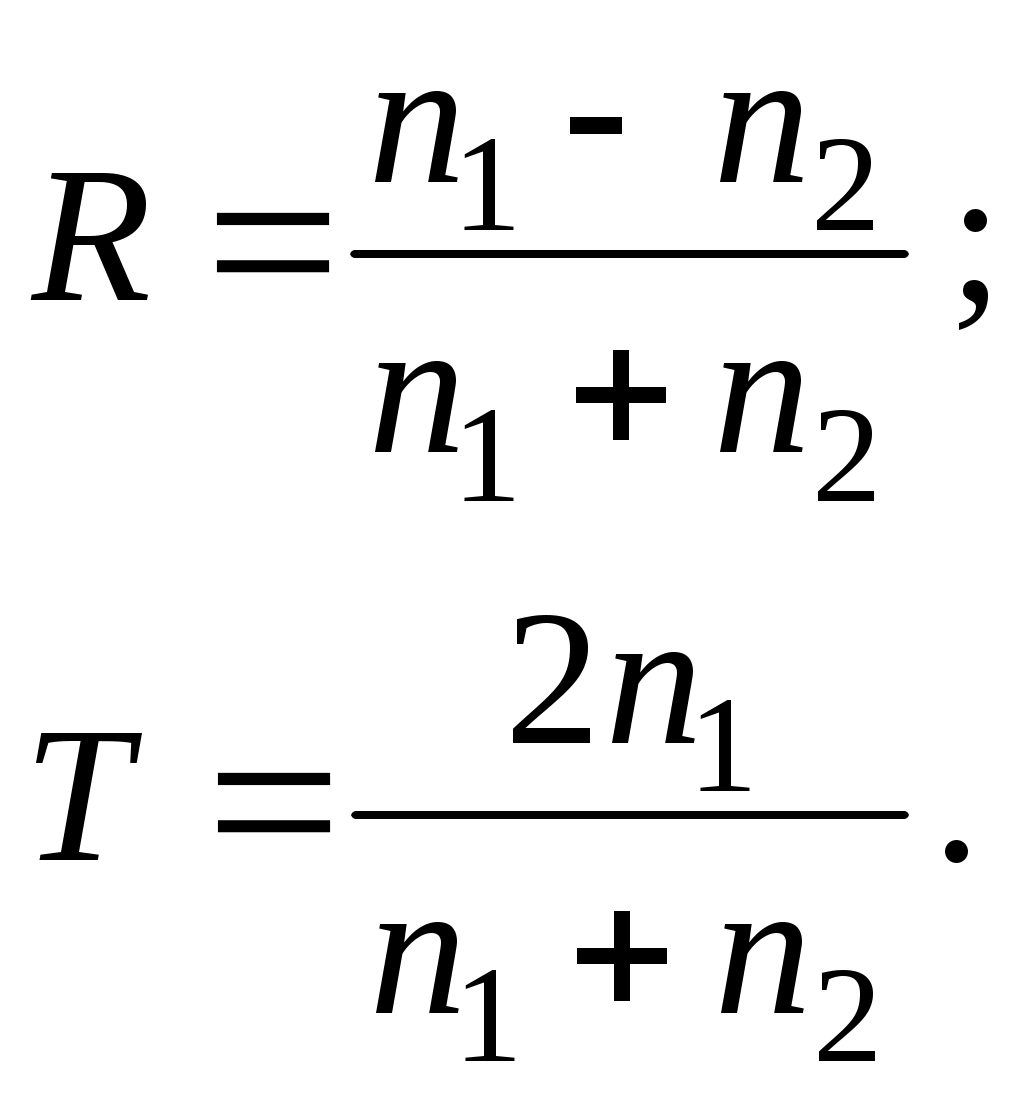 (46) – (47)
(46) – (47)1.5. Энергетические соотношения при отражении и преломлении света
Энергетическим коэффициентом отражения
Энергетический коэффициент пропускания
Т.к. ,
то для Â имеем:
или с учетом (30), (31), (41), (42):
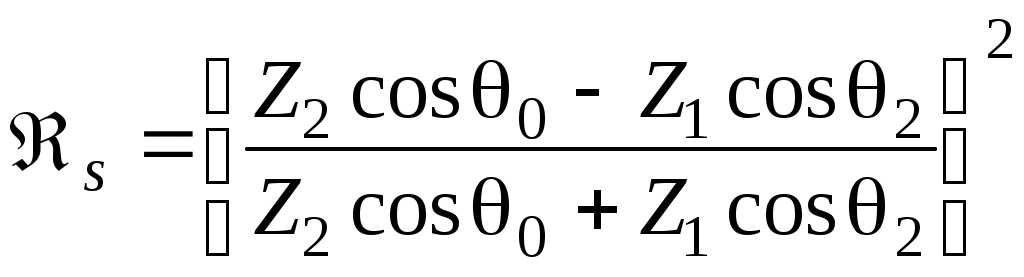 ; (54)
; (54)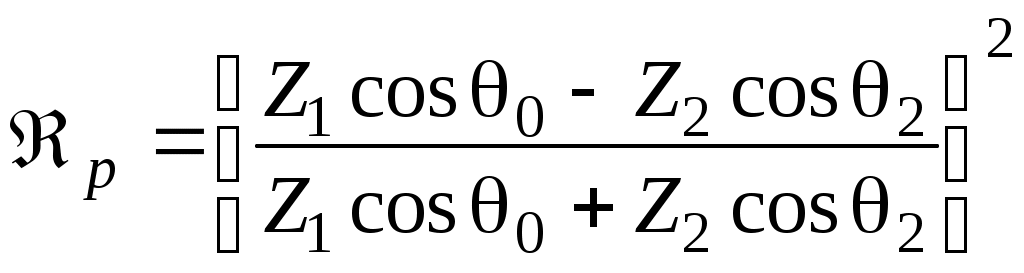 ; (55)
; (55)При q0 = 0 для m1 = m2
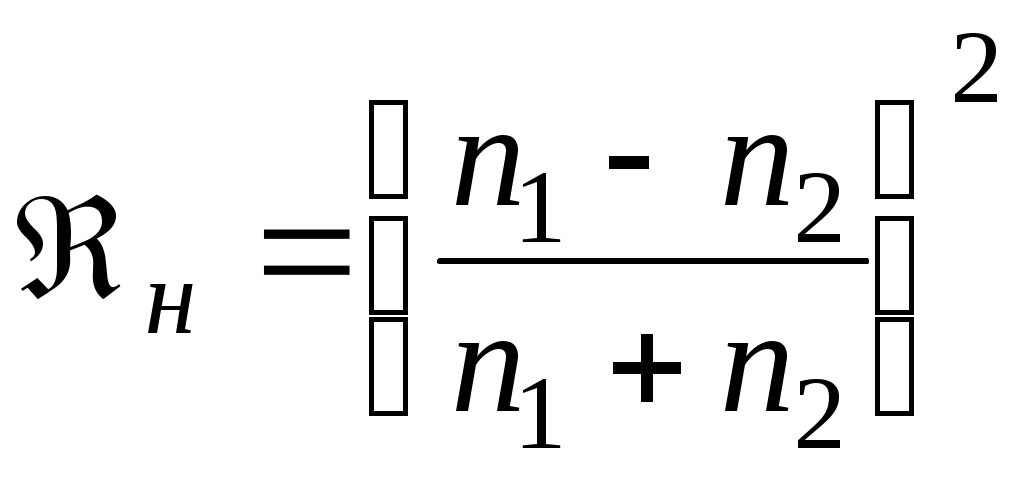 ; (58)
; (58)Прямой проверкой можно показать, что
 Рис. 9
Рис. 9Это выражает закон сохранения энергии при отражении и преломлении света на границе раздела двух сред. Графики для
2. Описание установки
Лабораторная установка (рис. 10) состоит из маломощного непрерывного лазера ((1) - излучатель, (2) – источник питания лазера), стеклянной плоскопараллельной пластины (3) с показателем преломления n=1.5, укрепленной на лимбе, имеющем градусную меру, фотоприемника (4) с цифровым индикатором и блоком питания (5). Показания цифрового индикатора фотоприемника (фототок) пропорциональны интенсивности света, падающего на фотоприемник. Излучение лазера линейно поляризовано. Все оптические элементы размещены на оптической скамье (6).

Рис.10. Схема лабораторной установки
3. Порядок выполнения работы
3.1. Установить оптические элементы, входящие в состав установки, на скамью. Проверить с помощью преподавателя правильное соединение элементов электрической части установки.
ВНИМАНИЕ!
В установке используется высокое напряжение и лазерное излучение. Приборы включают только инженер или преподаватель!
3.2. После включения приборов убрать стойку с пластиной, съюстировать оптические элементы так, чтобы луч, пройдя все элементы, попадал на фотоприемник (по максимуму фототока). Измерить фототок, соответствующий интенсивности падающей на пластину световой волны. Установить стойку с пластиной на место. Повторить юстировку.
3.3. Перекрыв лазерное излучение возле самого лазера, измерить темновой ток. В дальнейшем из показаний фотоприемника необходимо вычитать это значение.
3.4. Выставить плоскость поляризации излучения лазера перпендикулярно плоскости падения на стеклянную пластину. При необходимости повторить юстировку.
3.5. Снять зависимость фототока от угла падения света на пластину в диапазоне углов от 0 до 80 градусов с шагом 5 градусов. Угол падения устанавливается поворотом лимба. При изменении угла падения на каждом шаге необходимо подъюстировать фотоэлемент (по максимуму фототока). Измерения повторить не менее трёх раз.