Файл: Практикум волгоград 2014 Печатается по решению редакционноиздательского совета.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 261
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
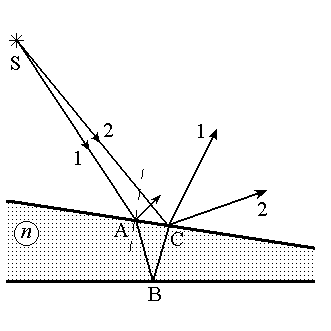
Рис. 2
Полосы равной толщины. Теперь рассмотрим интерференцию света на пластинке с переменной толщиной (клине) (рис.2). В световом потоке, исходящем из источника S монохроматического света всегда присутствует волна 2, интерферирующая в точке C с волной 1, прошедшей по пути SABC. Если источник расположен достаточно далеко от поверхности клина и угол между поверхностями клина достаточно мал (эти условия на практике при изучении такой схемы интерференции, как правило, выполняются), то оптическая разность хода приблизительно определяется при прочих равных условиях толщиной клина в точке Cи высчитывается по той же формуле, что и (9). Однако в этом случае интерференционная картина локализована на верхней поверхности клина. Интерференционную картину можно также наблюдать и с помощью линзы на экране. В этом случае поверхность проецируется на экран наблюдения. Линии одинаковой интенсивности совпадают с линиями постоянной толщины пластины, поэтому соответствующие интерференционные полосы называются полосами равной толщины. Ограничения на толщину клиновидной пластины, связанные со степенью временной когерентности (или монохроматичности) такие же, как и в случае плоскопараллельной пластины.
1.3. Кольца Ньютона
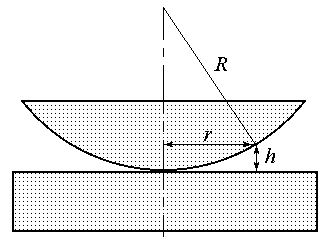
Рис. 3
Примером интерференционной схемы, в которой наблюдаются полосы равной толщины, является воздушная прослойка, образованная между плоской поверхностью стекла и положенной на нее плосковыпуклой линзой (или наоборот) (рис.3). В этом случае линии равной толщины – окружности, поэтому интерференционная картина имеет вид концентрических колец. Потеря полволны происходит на нижней поверхности воздушного клина. Пусть h – толщина воздушного клина в точке минимума картины (темное кольцо), R – радиус кривизны линзы. Найдем радиус темного интерференционного кольца m-го порядка. Из геометрии рисунка видно, что
Учитывая, что
m-го темного кольца:
Отметим, что используя условие максимума (10), аналогично можно получить выражение для радиуса m-го светлого кольца:
Следовательно, измерив радиус m-го интерференционного кольца и зная радиус кривизны линзы, можно определить длину волны света (или решить обратную задачу).
Интерференционные кольца наблюдаются как в отраженном, так и в прошедшем свете. При этом там, где в отраженном свете наблюдается светлое кольцо, в прошедшем – темное, т.е. интерференционные картины в прошедшем и отраженном свете являются взаимно дополнительными. Центральное пятно в отраженном свете – темное, т.к. толщина воздушного клина пренебрежимо мала, и волны интерферируют практически в противофазе из-за потери полволны. В белом свете, как и следует из формул (13, 14), наблюдаются цветные кольца.
Контрастность интерференционных картин в отраженном и прошедшем свете неодинакова. Для наблюдения четкой интерференционной картины в отраженном свете поверхности клина должны обладать малым коэффициентом отражения, а в прошедшем – большим. Это легко видеть из соотношений амплитуд интерферирующих волн, которые для лучшей видимости должны стремиться к единице. Для отраженных волн оно равно
2. Описание установки
Лабораторная установка (рис. 4) состоит из маломощного непрерывного лазера ((1) – излучатель, (2) – источник питания лазера), ртутной лампы ((3) – излучатель, (4) – источник питания лампы), стеклянных светофильтров (5), бинокулярного микроскопа МБС-9, световода (6), закрепленного в оправе (7), системы «линза-пластинка» (9). Все оптические элементы размещены на оптической скамье (8). По световоду свет через один из окуляров попадает на систему «линза-пластинка», помещенную на предметном столике (10) микроскопа. Для измерения диаметра колец Ньютона используется шкала, закрепленная в окуляре микроскопа. При положении «4» на шкале увеличений (
11) объектива микроскопа, цена малого деления окуляра составляет 0,25 мм. При помощи ручки (12) осуществляется фокусировка микроскопа на объект. Открепив винт (13), можно вращать при необходимости оптическую головку (14) на 180° в горизонтальной плоскости.
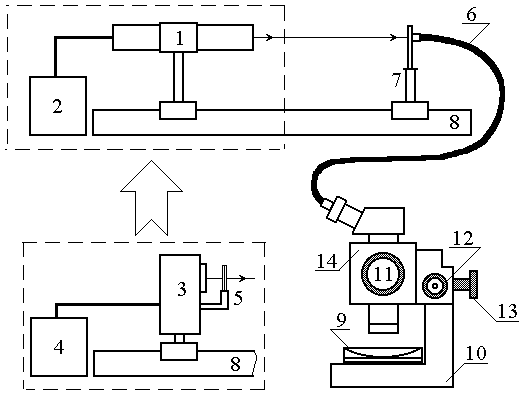
Рис. 4. Схема лабораторной установки
3. Порядок выполнения работы
3.1. Определение радиуса кривизны линзы
3.1.1. Поставить в положение «4» шкалу (11) объективной части микроскопа и не менять этого положения в процессе всей работы.
3.1.2. Включить лазер тумблером на панели блока питания, при этом должна загореться лампочка рядом с тумблером. Через 1-2 с. начнется генерация лазерного излучения.
3.1.3. Направить излучение лазера на входное отверстие световода.
3.1.4. Глядя в окуляр микроскопа, совместить центр интерференционной картины с центром поля окуляра, осторожно перемещая систему «линза-пластинка» на предметном столике.
3.1.5. Перемещая световод по полю окуляра, снять отсчеты в точках пересечения 3, 4, 5, 6, 7-го темных колец со шкалой пять раз. Номера колец отсчитываются от центра интерференционной картины в направлении увеличения значений шкалы
3.1.6. Повторить п.3.1.5., отсчитывая номера колец, в направлении уменьшения значений шкалы
3.1.7. Определить диаметры 3, 4, 5, 6, 7-го темных колец как разность соответствующих отсчетов в обоих направлениях с учетом цены малого деления окуляра.
3.1.8. Найти среднее значение диаметра для каждого кольца.
3.1.9. Определить радиус кривизны линзы по формуле
Rn+1, n= (D2n+1 – D2n) / 4λлаз (15`)
где n = 3, 4, 5, 6.
3.1.10. Провести статистическую обработку результатов с доверительной вероятностью 90%.
3.2. Определение длин волн ртутного спектра по кольцам Ньютона
3.2.1. Заменить лазер ртутной лампой. Закрыть окно кожуха лампы светофильтром, выделяющим зеленую линию ртутного спектра. Для этого использовать сразу два фильтра ПС-7 и ЖС-17 (или аналогичные, указанные преподавателем).
3.2.2. Проделать п.п. 3.1.4.–3.1.8. Определить длину волны зеленой линии ртутного спектра, используя найденное выше значение Rср и формулу (15`).
3.2.3. Провести статистическую обработку результатов с доверительной вероятностью 90%.
3.2.4. Проделать п.п. 3.2.1.–3.2.3., выделив из ртутного спектра желтую, синюю линии, используя при этом фильтры ОС-13, ЖЗС-18 и ПС-11, ЖС-11 соответственно (или аналогичные, указанные преподавателем).
3.2.5. Занести результаты в таблицу 1.
Таблица 1. Определение радиуса кривизны линзы по темным кольцам Ньютона
| nтемного кольца | Отсчет по шкале | D мм | Dср мм | σD мм | R n+1, n мм | Rср мм | σR мм | ∆R мм | |
| в направлении увеличения значений | в направлении уменьшения значений | ||||||||
| 3 | | | | | | ______ ______ ______ | | | |
| | | | |||||||
| | | | |||||||
| | | | |||||||
| | | | |||||||
| 4 | | | | | | ||||
| | | | |||||||
| | | | |||||||
| | | | |||||||
| | | | |||||||
| 5 | | | | | | ||||
| | | | |||||||
| | | | |||||||
| | | | |||||||
| | | | |||||||
| 6 | | | | | | ||||
| | | | |||||||
| | | | |||||||
| | | | |||||||
| | | | |||||||
| 7 | | | | | | ||||
| | | | |||||||
| | | | |||||||
| | | | |||||||
| | | | |||||||
Таблица 2. Определение длин волн ртутного спектра по темным кольцам Ньютона
| nтемного кольца | Отсчет по шкале | D мм | Dср мм | σD мм | R n+1, n мм | λn+1, n нм | λ ср мм | σλ мм | ∆λ мм | |
| в направлении увеличения значений | в направлении уменьшения значений | |||||||||
| 3 | | | | | | ______ ______ ______ | ______ ______ ______ | | | |
| | | | ||||||||
| | | | ||||||||
| | | | ||||||||
| | | | ||||||||
| 4 | | | | | | |||||
| | | | ||||||||
| | | | ||||||||
| | | | ||||||||
| | | | ||||||||
| 5 | | | | | | |||||
| | | | ||||||||
| | | | ||||||||
| | | | ||||||||
| | | | ||||||||
| 6 | | | | | | |||||
| | | | ||||||||
| | | | ||||||||
| | | | ||||||||
| | | | ||||||||
| 7 | | | | | | |||||
| | | | ||||||||
| | | | ||||||||
| | | | ||||||||
| | | | ||||||||